Similar presentations:
Плоские фермы. Определения. Модель плоской фермы
1. Плоские фермы
2.
Плоские фермы. Определения
Модель плоской фермы
Определение реакций опор плоской фермы
Определение усилий в стержнях плоской
фермы
• Алгоритм метода вырезания узлов
• Алгоритм метода сечений (Риттера)
• Нулевые стержни плоской фермы
3. Плоские фермы. Определения
• Плоские фермы – геометрически неизменяемыестержневые конструкции, стержни которых
принадлежат в одной плоскости
• Узлы фермы – точки, в которых сходятся оси стержней
• Верхний и нижний пояс – стержни, образующие
верхний и нижний контуры, соответственно
• Стойки – вертикальные стержни.
• Раскосы – наклонные стержни.
• Пролет фермы – расстояние между опорными узлами
• Длина панели – расстояние между стойками
4. Плоские фермы. Определения
F52
F4
4
16
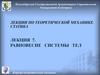
Шарниры 1,2,…,10 - узлы фермы
Стержни 7-8, 8-9, 9-10, 10-1 - нижний пояс
Стержни 2-3, 3-4, 4-5, 5-6 - верхний пояс
Стержни 1-2, 3-10, 4-9, 5-8, 6-7 - стойки
Стержни 2-10, 4-10, 4-8, 6-8 - раскосы
Пролет фермы составляет 16
Длина панели между 1-2 и 3-10 равна 4
2,5
F3
F2
F1
5.
Рисунок 1 – Металлическаяконструкция для освещения из
плоских ферм
Рисунок 2 – Металлическая плоская
ферма сцены
6.
Рисунок 3 – Металлические плоские фермы ангара7. Модель плоской фермы
• Предполагаем:1.
2.
3.
стержни прямолинейные, невесомые
внешние силы приложены только к узлам фермы
узлы – идеальные шарниры
• Задача расчета фермы – определение реакций опор
(внешних реакций связей) и усилий в стержнях
(внутренних реакций связей) фермы
• Для статически определимых ферм
1.
2.
число неизвестных в системе уравнений, описывающей
условие равновесия фермы не больше числа независимых
уравнений
число стержней N связано с числом узлов n равенством
N=2n-3
8. Модель плоской фермы
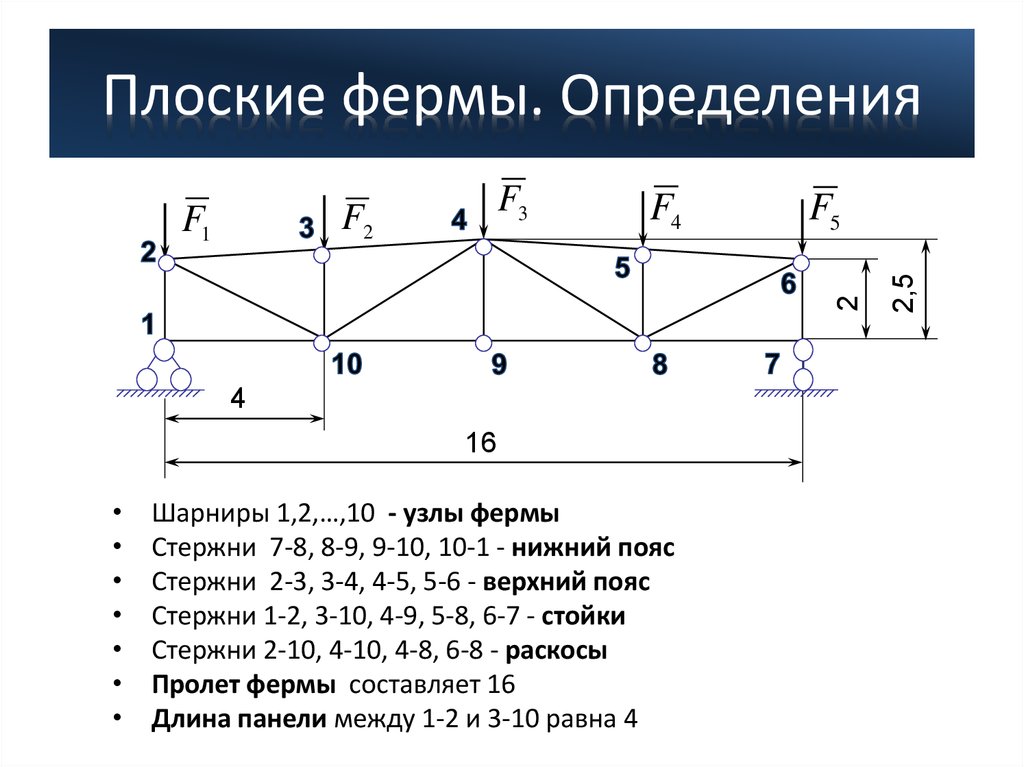
• Задание 1. Является ли ферма статическиопределимой?
F5
2
F4
4
16
2,5
F3
F2
F1
9. Определение реакций опор плоской фермы
• Задание 2. Найти реакции опор фермыесли F F 5 кН , F F F 11 кН ; линейные
размеры фермы приведены в метрах
5
2
3
F3
F2
F4
F5
2
F1
4
4
16
2,5
1
10.
Система внешних сил фермы – плоская произвольная система сил,следовательно условие равновесия системы сил имеет вид:
X 0
Y 0
M узел1 0
X 0
5
Fi Y1 Y7 0
i 1
F2 4 F3 8 F412 F516 Y716 0
X 0, Y1 Y7 21,5кН
y
F4
Y7
Y1
2,5
F5
2
F3
F2
F1
x
X1
4
16
11.
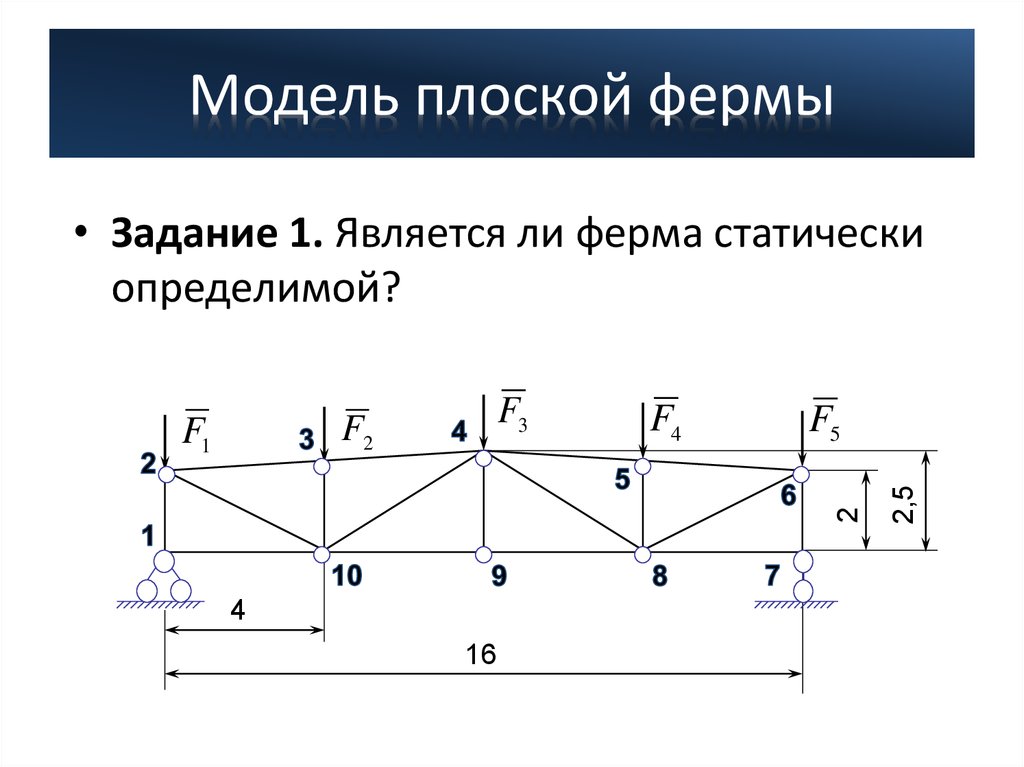
• Задание 3. Показать реакции опор фермыОпорный стержень
F2
F1
Y1
X2
X1
F3
F4
F5
12. Определение усилий в стержнях плоской фермы
• Методом вырезания узлов : последовательно вырезаем узлыфермы так, чтобы рассматриваемый узел являлся статически
определимым, то есть в двух уравнениях равновесия плоской
сходящейся системы сил для каждого из узлов было не более
двух неизвестных усилий.
• Методом сечений (Риттера): проводим сечение фермы по
трем стержням с неизвестными усилиями и составляем
уравнение равновесия одной части фермы, используя вторую
(третью) форму системы линейных уравнений произвольной
плоской системы сил
• ! Опорные реакции фермы должны быть предварительно
определены.
13. Алгоритм метода вырезания узлов
1.2.
3.
4.
5.
6.
7.
8.
Определить опорные реакции фермы: выбрать в качестве объекта
равновесия ферму в целом
Пронумеровать узлы фермы
Найти нулевые стержни (если существуют)
Найти узел, в котором сходятся два стержня с неизвестными усилиями
Разрезать стержни в окрестности этого узла, направить усилия от узла в
предположении, что стержень растянут
Выбрать в качестве объекта равновесия этот узел
Найти усилия стержней, связанных с этим узлом, из системы линейных
уравнений равновесия плоской сходящейся системы сил
Повторить алгоритм с пункта 4
! Если усилие направлено от узла, то оно вызывает растяжение стержня, и
положительно. Если усилие направлено к узлу, то вызывает сжатие стержня, и
отрицательно.
14. Алгоритм метода сечений (Риттера)
1. Определить опорные реакции фермы: выбрать в качестве объекта равновесияферму в целом
2. Пронумеровать узлы фермы
3. Провести сечение фермы по трем стержням с неизвестными усилиями
4. Выбрать в качестве объекта равновесия одну из частей фермы
5. Направить усилия разрезанных стержней от узлов, принадлежащих этой части,
в предположении, что стержни растянуты
6. Найти усилия разрезанных стержней из системы линейных уравнений
равновесия произвольной плоской системы сил в третьей форме (или во
второй форме, если два стержня, усилия которых неизвестны, параллельны):
2) X 0, M M1 0, M M 2 0,
причем ось x не перпендикулярна M 1M 2
3) M M1 0,
M
M2
0,
M
M2
0,
M 1 , M 2 , M 3 точки Риттера
(точки пересечения линий действия двух неизвестных усилий )
7. Повторить алгоритм с пункта 3
15. Нулевые стержни плоской фермы
• Стержни называются нулевыми, если усилия в нихравны нулю
• Условия существования нулевых стержней:
1.
2.
3.
Если к узлу с двумя стержнями, которые не принадлежат
одной прямой, не приложена внешняя нагрузка, то усилия
в них равны нулю
Если в узле сходятся три стержня, причем два принадлежат
одной прямой и нагрузка в узле отсутствует, то в третьем
стержне, не принадлежащем этой прямой, усилие равно
нулю
Если в узле сходятся два стержня, а нагрузка направлена
вдоль оси одного из них, то усилие в другом равно нулю
16.
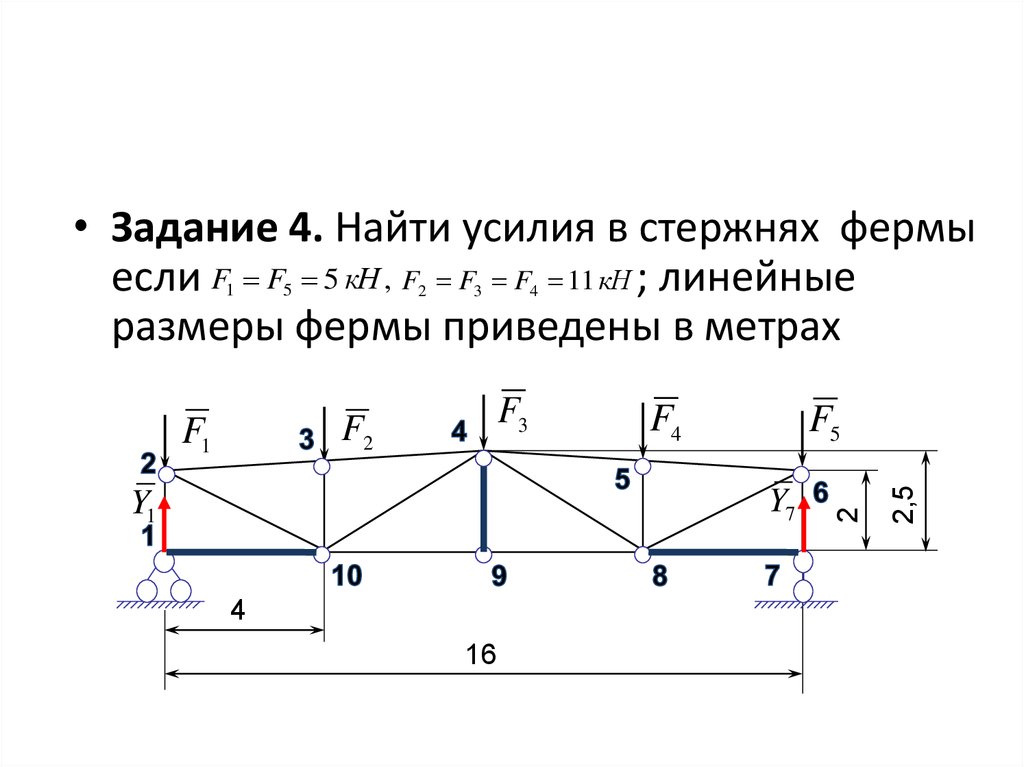
• Задание 4. Найти усилия в стержнях фермыесли F F 5 кН , F F F 11 кН ; линейные
размеры фермы приведены в метрах
2
3
F3
F2
F1
4
F4
F5
Y7
Y1
4
16
2,5
5
2
1
17.
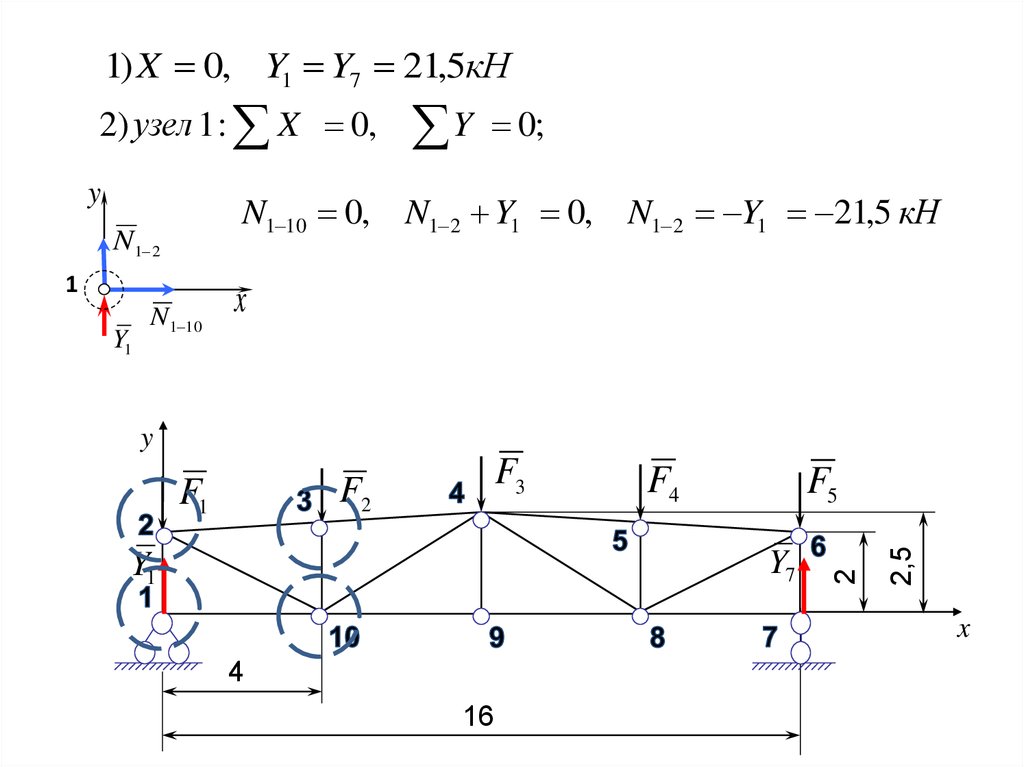
1) X 0, Y1 Y7 21,5кН2) узел 1 : X 0,
y
0;
N1 10 0, N1 2 Y1 0, N1 2 Y1 21,5 кН
N1 2
1
Y1
Y
N1 10
x
y
F4
Y7
Y1
2,5
F5
2
F3
F2
F1
x
4
16
18.
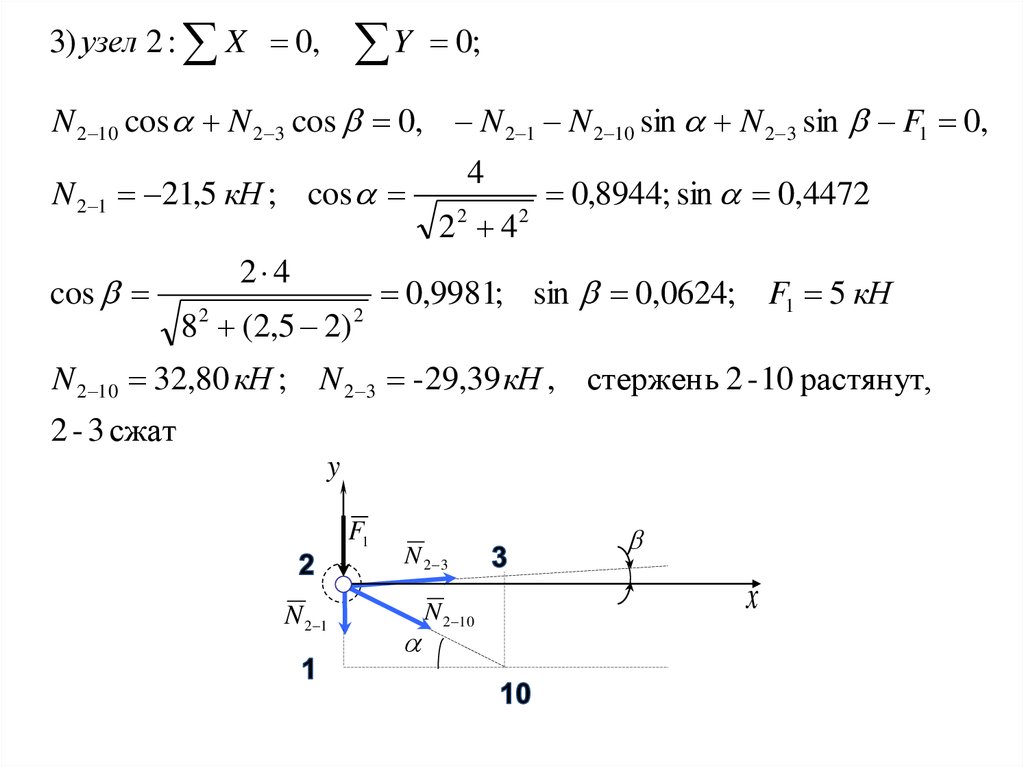
3) узел 2 : X 0,Y
0;
N 2 10 cos N 2 3 cos 0, N 2 1 N 2 10 sin N 2 3 sin F1 0,
N 2 1 21,5 кН ; cos
cos
2 4
8 (2,5 2)
2
2
4
2 4
2
2
0,8944; sin 0,4472
0,9981; sin 0,0624; F1 5 кН
N 2 10 32,80 кН ; N 2 3 -29,39 кН , стержень 2 - 10 растянут,
2 - 3 сжат
y
F1
N 2 1
N 2 3
N 2 10
x
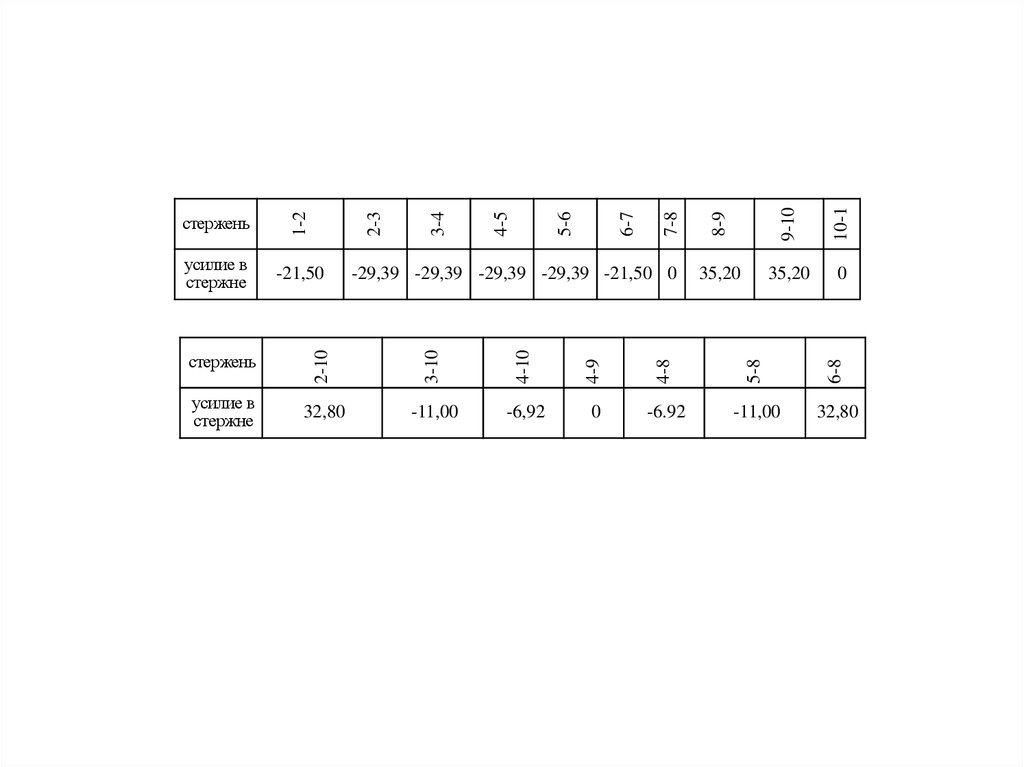
19.
10-16-8
9-10
стержень
5-8
0
4-8
35,20
4-9
8-9
7-8
6-7
5-6
4-5
35,20
4-10
-29,39 -29,39 -29,39 -29,39 -21,50 0
3-10
-21,50
3-4
2-3
1-2
усилие в
стержне
2-10
стержень
усилие в
стержне
32,80
-11,00
-6,92
0
-6.92
-11,00
32,80
20.
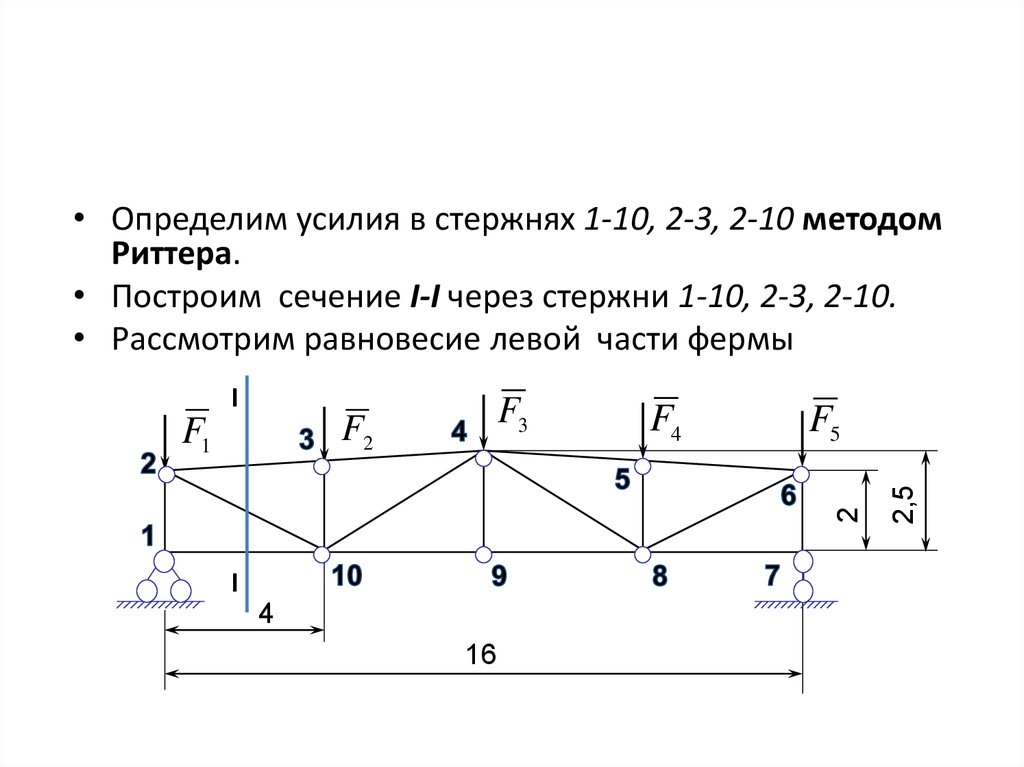
• Определим усилия в стержнях 1-10, 2-3, 2-10 методомРиттера.
• Построим сечение I-I через стержни 1-10, 2-3, 2-10.
• Рассмотрим равновесие левой части фермы
F3
F2
F4
F5
2
F1
I
4
16
2,5
I
21.
Mузел10
M
0,
4 F1 4VA N 2 3d 2 0,
узел 2
0,
2 N1 10 0,
M
M1
0,
M 1 A(VA F1 ) N 2 10d1 0
M1 A 4
32 4
M 1 A 2ctg 2 16 32 м, d 2
2
2 2,25 м
M1 A
32
d1 ( M 1 A 4) sin (32 4) 0,4772 16,1м,
N1 10 0кН , N 2 3 -29,39 кН , N 2 10 32,80 кН
d1
М1
F1
I N 2 3
2
N 2 10 d 2
I N1 10
10
А
1 Y
1
3













 physics
physics