Similar presentations:
Равновесие при наличии трения
1. Новосибирский Государственный Архитектурно- Строительный Университет (Сибстрин)
Новосибирский Государственный АрхитектурноСтроительный Университет (Сибстрин)Лекция 5.
РАВНОВЕСИЕ ПРИ НАЛИЧИИ
ТРЕНИЯ
Каждым тяжелым телом побеждается
сопротивление трения, равное четвертой
части этого веса.
Леонардо да Винчи
Кафедра теоретической механики
2.
Леонардо да Винчи1452-1519, Италия
2
3.
Музей Леонардо да ВинчиВенеция, Италия
3
4.
45.
56. … и когда они ели, сказал: истинно говорю вам, что один из вас предаст Меня
67. На предыдущей лекции
• Были изучены методы расчетаплоских ферм и плоских составных
конструкций
• До сих пор, однако, изучались лишь
системы, в которых отсутствуют
силы трения
7
8. Цель лекции
• Познакомиться с решением задач статикипри наличии силы трения
• Ввести понятие центра тяжести тела и
познакомиться с методами его расчета
План лекции
5.1. Сила трения покоя
5.2. Сила трения скольжения
5.3. Условия равновесия при наличии трения
5.4. Трение качения
5.5. Центр тяжести
5.6. Методы расчета центра тяжести
5.7. Заключение
8
9. 5.1. Сила трения покоя
10. 5.1.1. Сила трения покоя
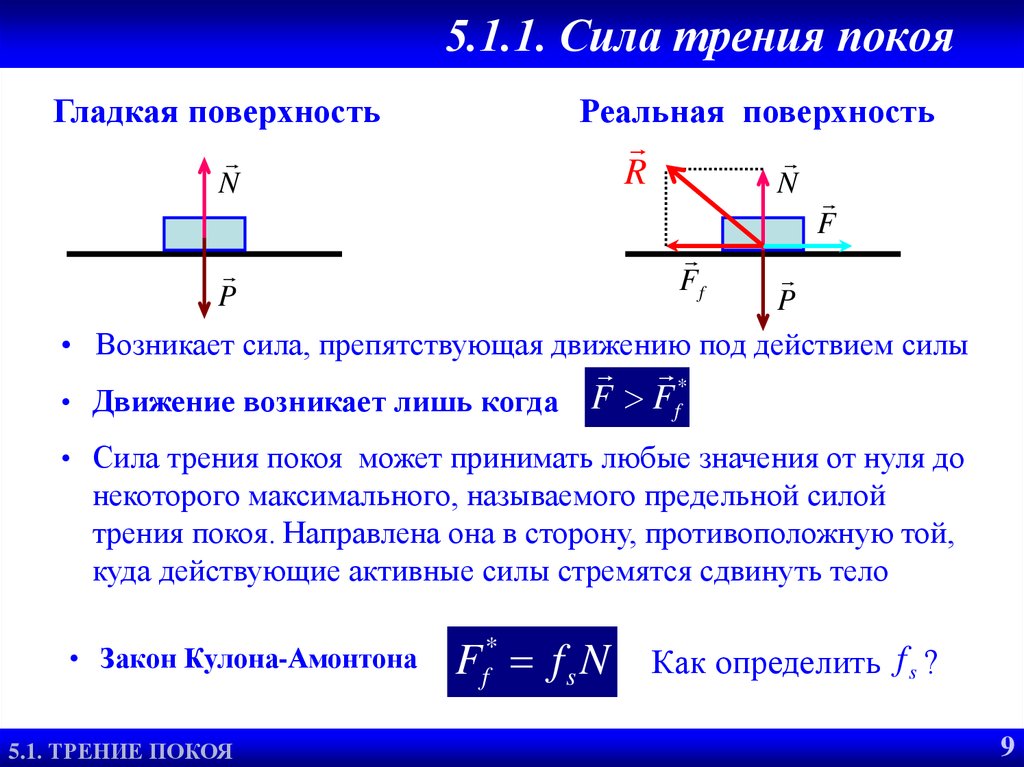
Гладкая поверхностьРеальная поверхность
R
N
Ff
P
N
F
P
• Возникает сила, препятствующая движению под действием силы
*
• Движение возникает лишь когда F Ff
• Сила трения покоя может принимать любые значения от нуля до
некоторого максимального, называемого предельной силой
трения покоя. Направлена она в сторону, противоположную той,
куда действующие активные силы стремятся сдвинуть тело
• Закон Кулона-Амонтона
2.1.
ОПРЕДЕЛЕНИЕ
5.1. ТРЕНИЕ
ПОКОЯССС
F fs N
*
f
Как определить f s ?
9
11. 5.1.2. Определение коэффициента трения покоя
NF
fs F / P
Ff
*
f
P
A
• Коэффициент трения покоя (статический коэффициент трения)
определяется лишь свойствами материалов соприкасающихся тел и не
зависит от площади контакта этих тел
Материал
fs
сплав пона
стали
(без смазки)на тело действует
0.2
•Медно-свинцовый
Поверхность,
которой
Тщательно очищенные металлы по металлу
100
сила
трения,
будем называть шероховатой
Стекло
по стеклу,
очищенные
1
Дерево по металлу, сухое и очищенное
0.2–0.6
Кожа по металлу, очищенная сухая
0.6
2.1.
ССС
5.1. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ ПОКОЯ
10
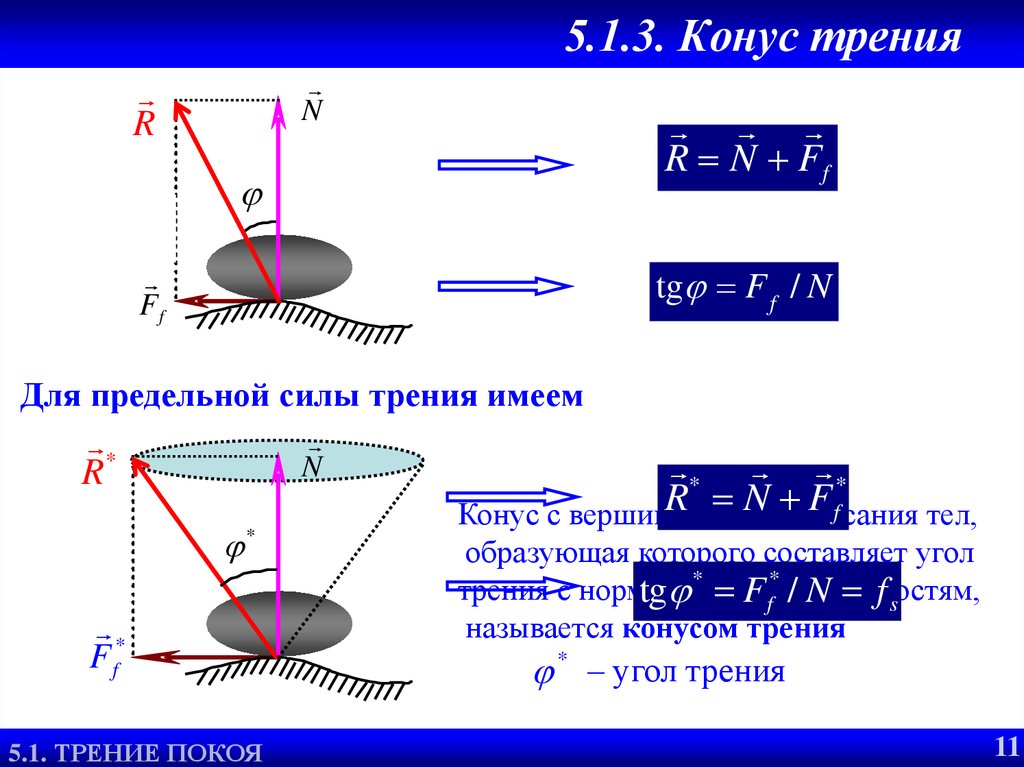
12. 5.1.3. Конус трения
NR
R N Ff
tg F f / N
Ff
Для предельной силы трения имеем
*
R
N
*
*
Ff
2.1.
ССС
5.1. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ ПОКОЯ
* *
R в точке
N Fкасания
f
Конус с вершиной
тел,
образующая которого составляет угол
трения с нормалью
ихf* поверхностям,
tg * к F
/ N fs
называется конусом трения
* – угол трения
11
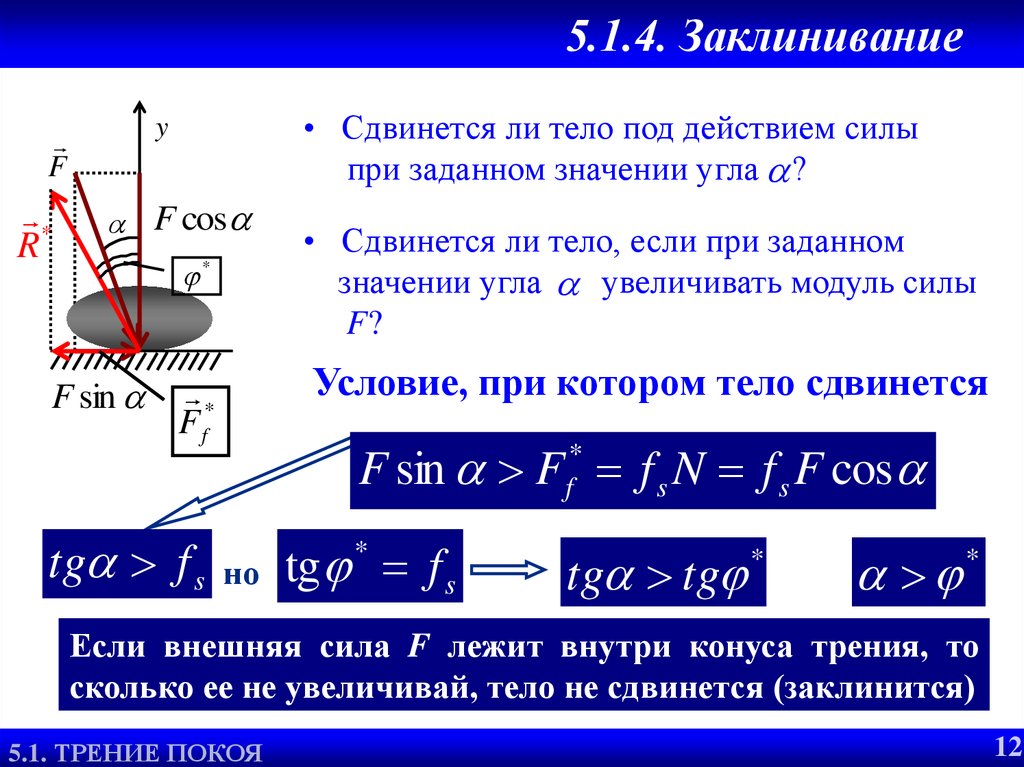
13. 5.1.4. Заклинивание
*R
• Сдвинется ли тело под действием силы
при заданном значении угла ?
y
F
F cos
*
F sin
Условие, при котором тело сдвинется
*
Ff
tg f s
• Сдвинется ли тело, если при заданном
значении угла увеличивать модуль силы
F?
F sin F f s N f s F cos
*
f
но
tg f s
*
tg tg
*
*
Если внешняя сила F лежит внутри конуса трения, то
сколько ее не увеличивай, тело не сдвинется (заклинится)
2.1.
ССС
5.1. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ ПОКОЯ
12
14. 5.1.5. Задача 5.1
F f*y
N
Q
30
х
P
Определить силу Q, направленную под углом
30° к горизонту, которую необходимо
приложить к грузу веса P = 10 кН, чтобы
сдвинуть его с места, если коэффициент
трения fs = f = 0.6.
Решение
• Введем систему координат, считая тело материальной точкой
• Составим уравнения предельного равновесия груза
Fix 0,
F f* Q cos 30 0
Fiy 0,
N P Q sin 30 0
i
i
Но
F fN
*
f
ТРЕНИЕ
2.1.
СКОЛЬЖЕНИЯ
ССС
5.1. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
ПОКОЯ
Q fP /(cos 30 f sin 30 ) 5,2(kH )
13
15. 5.2. Сила трения скольжения
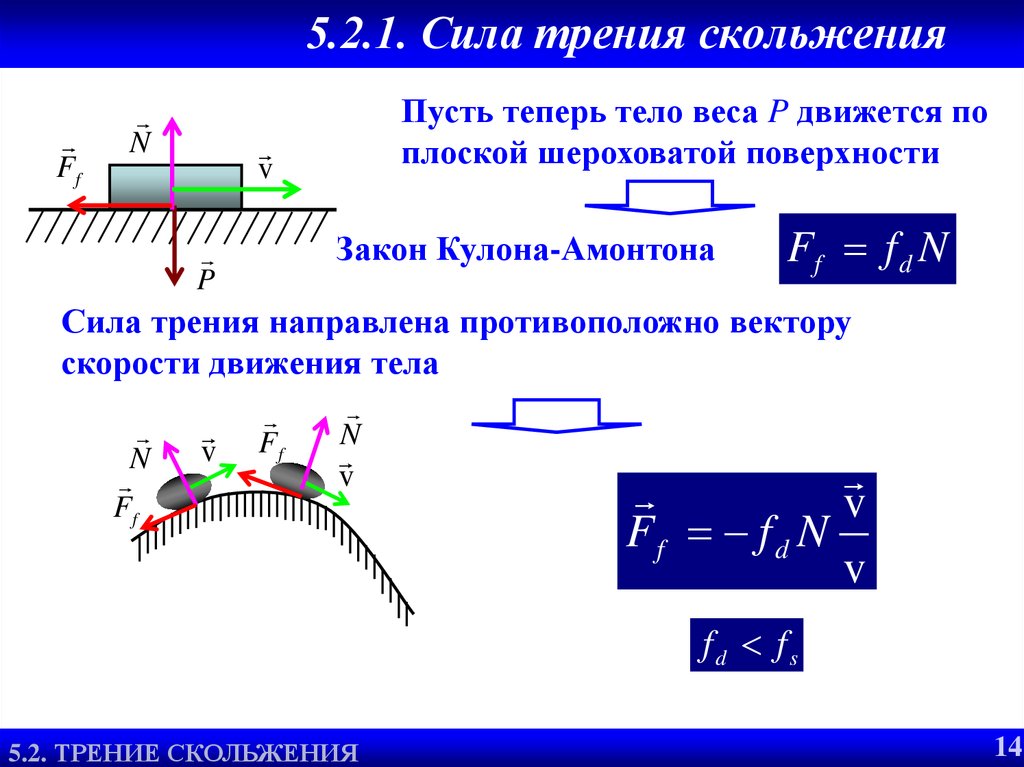
16. 5.2.1. Сила трения скольжения
FfN
Пусть теперь тело веса P движется по
плоской шероховатой поверхности
v
Закон Кулона-Амонтона
P
Ff f d N
Сила трения направлена противоположно вектору
скорости движения тела
N
Ff
v
Ff
N
v
v
Ff f d N
v
fd fs
ТРЕНИЕ
2.1.
СКОЛЬЖЕНИЯ
ССС
5.2. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
СКОЛЬЖЕНИЯ
14
17. 5.3. Трение качения
18. 5.3.1. Сила трения качения
NQ
Ff
P
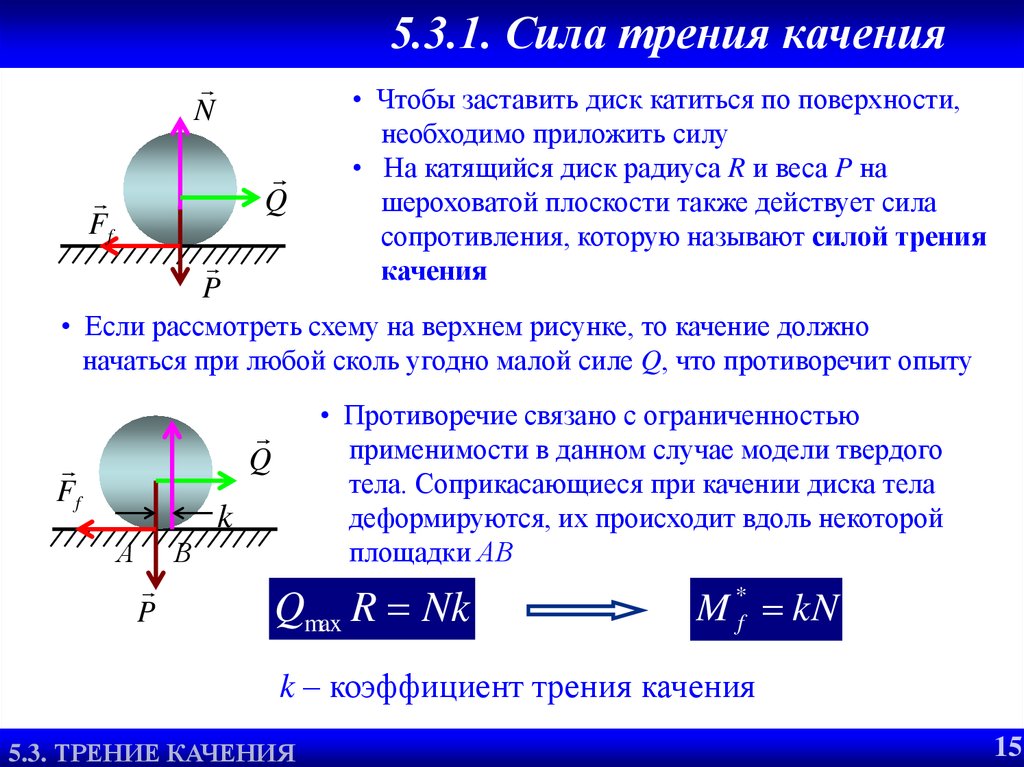
• Чтобы заставить диск катиться по поверхности,
необходимо приложить силу
• На катящийся диск радиуса R и веса P на
шероховатой плоскости также действует сила
сопротивления, которую называют силой трения
качения
• Если рассмотреть схему на верхнем рисунке, то качение должно
начаться при любой сколь угодно малой силе Q, что противоречит опыту
• Противоречие связано с ограниченностью
применимости в данном случае модели твердого
тела. Соприкасающиеся при качении диска тела
деформируются, их происходит вдоль некоторой
площадки АВ
Q
Ff
k
А
В
P
Qmax R Nk
M *f kN
k – коэффициент трения качения
ТРЕНИЕ
2.1.
СКОЛЬЖЕНИЯ
ССС
5.3. ОПРЕДЕЛЕНИЕ
ТРЕНИЕ
КАЧЕНИЯ
15
19. 5.4. Центр тяжести
20. 5.4.1. Определение центра тяжести
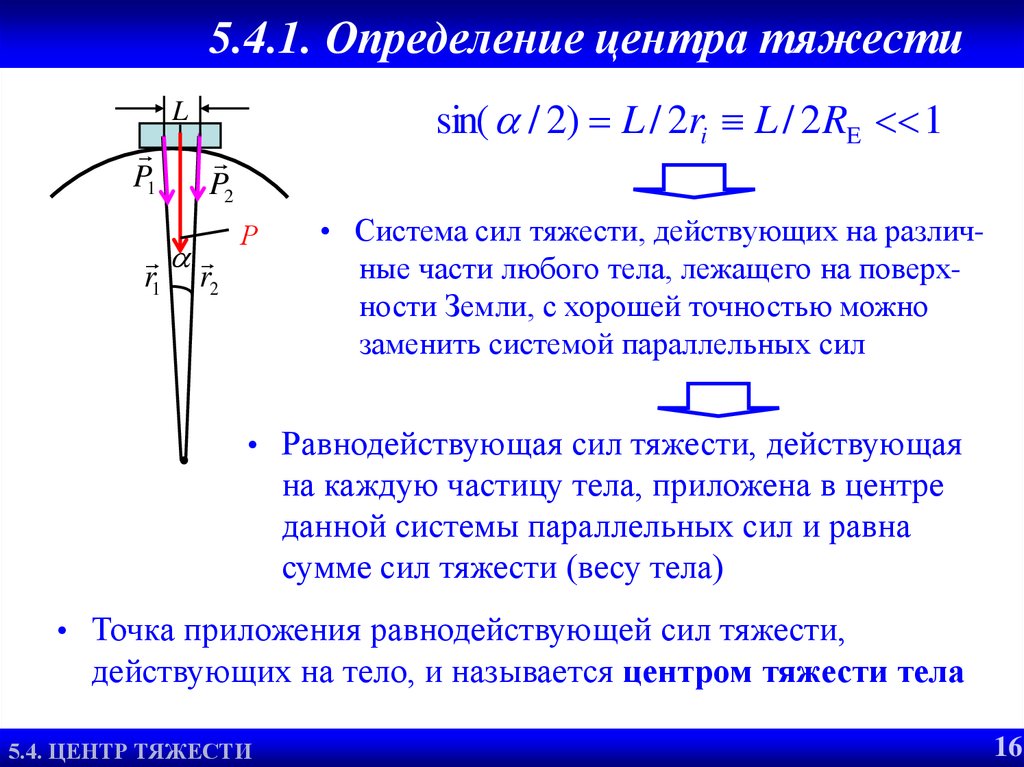
sin( / 2) L / 2ri L / 2RE 1L
P1
P2
r1 r2
• Система сил тяжести, действующих на различные части любого тела, лежащего на поверхности Земли, с хорошей точностью можно
заменить системой параллельных сил
Р
• Равнодействующая сил тяжести, действующая
на каждую частицу тела, приложена в центре
данной системы параллельных сил и равна
сумме сил тяжести (весу тела)
• Точка приложения равнодействующей сил тяжести,
действующих на тело, и называется центром тяжести тела
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
16
21. 5.4.2. Координаты центра тяжести
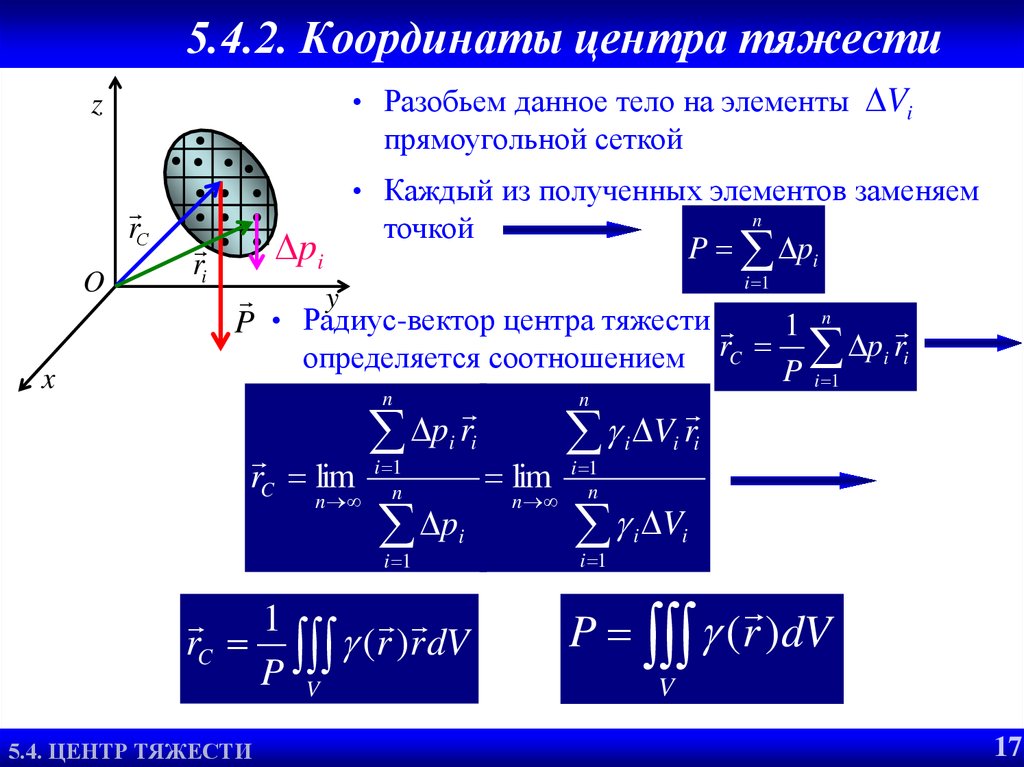
• Разобьем данное тело на элементыz
прямоугольной сеткой
rС
O
x
Vi
• Каждый из полученных элементов заменяем
ri
p i
точкой
n
P pi
i 1
y
P • Радиус-вектор центра тяжести
1 n
r
p
r
определяется соотношением C P i i
i 1
pi ri
n
rC lim
i 1
n
n
p
i 1
i
1
rC (r )r dV
P V
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
i Vi ri
n
lim
i 1
n n
V
i 1
i
i
P (r )dV
V
17
22. 5.4.3. Координаты центра тяжести
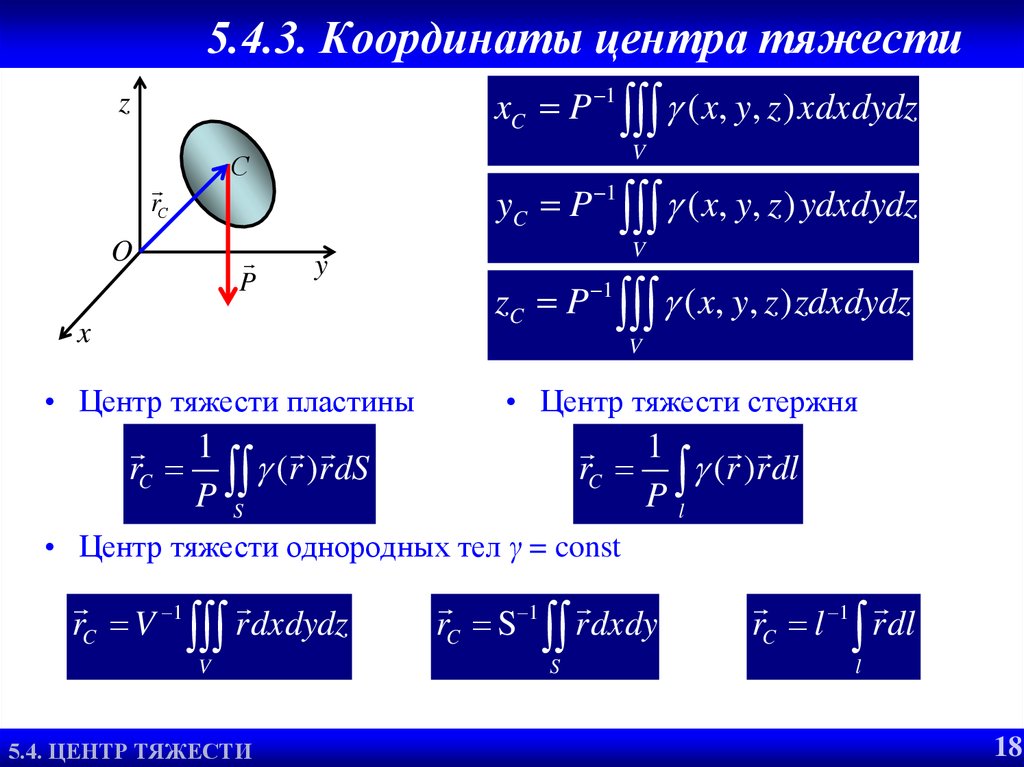
xC P 1 ( x, y, z ) xdxdydzz
V
С
rС
O
P
yC P 1 ( x, y, z ) ydxdydz
y
x
V
zC P 1 ( x, y, z ) zdxdydz
V
• Центр тяжести пластины
• Центр тяжести стержня
1
rC (r )r dS
P S
1
rC (r )r dl
Pl
• Центр тяжести однородных тел γ = const
1
rC V r dxdydz
V
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
1
rC S r dxdy
S
1
rC l r dl
l
18
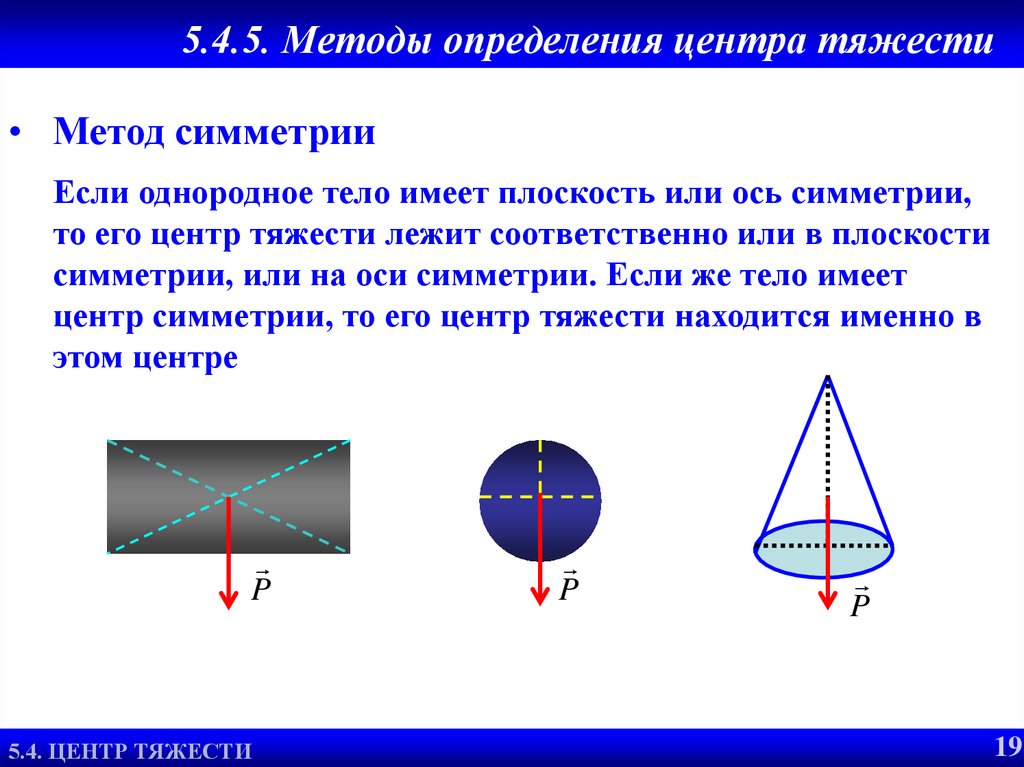
23. 5.4.5. Методы определения центра тяжести
• Метод симметрииЕсли однородное тело имеет плоскость или ось симметрии,
то его центр тяжести лежит соответственно или в плоскости
симметрии, или на оси симметрии. Если же тело имеет
центр симметрии, то его центр тяжести находится именно в
этом центре
P
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
P
P
19
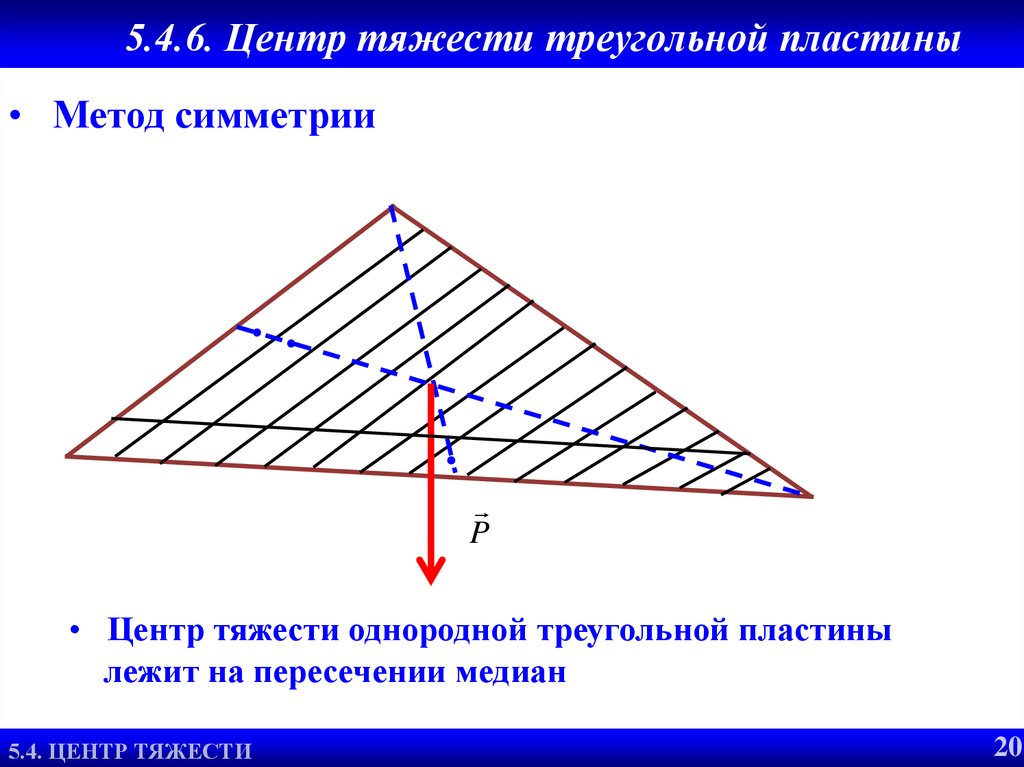
24. 5.4.6. Центр тяжести треугольной пластины
• Метод симметрииP
• Центр тяжести однородной треугольной пластины
лежит на пересечении медиан
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
20
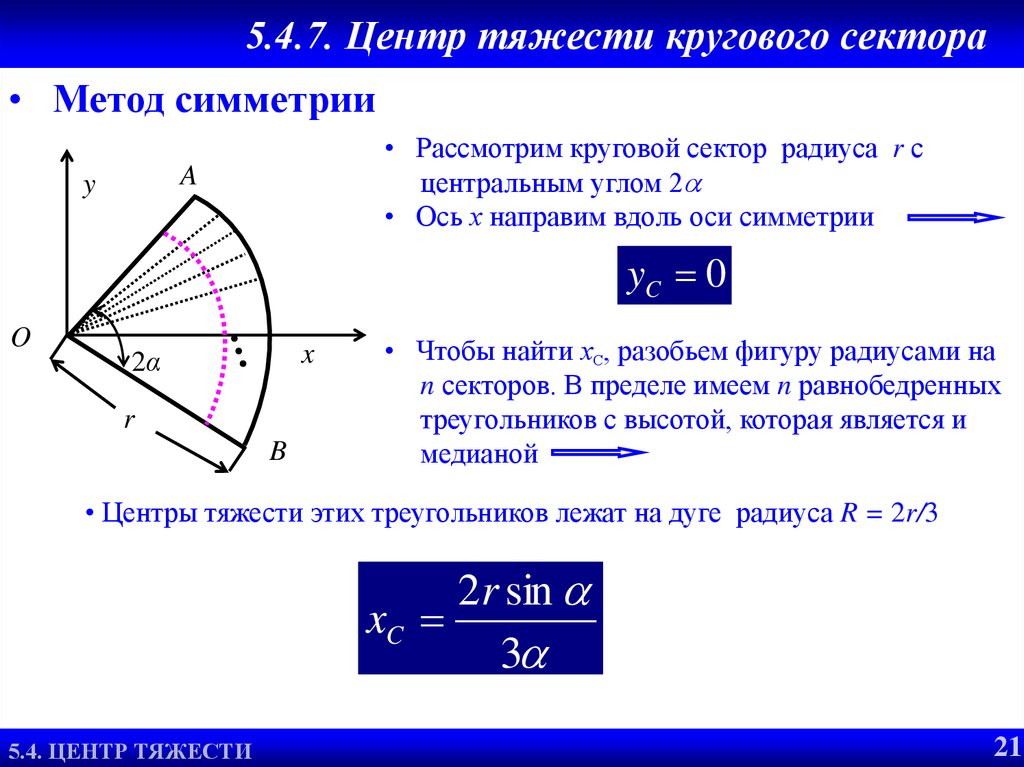
25. 5.4.7. Центр тяжести кругового сектора
• Метод симметрии• Рассмотрим круговой сектор радиуса r с
центральным углом 2
• Ось х направим вдоль оси симметрии
A
y
yC 0
O
x
2α
r
B
• Чтобы найти хС, разобьем фигуру радиусами на
n секторов. В пределе имеем n равнобедренных
треугольников с высотой, которая является и
медианой
• Центры тяжести этих треугольников лежат на дуге радиуса R = 2r/3
2r sin
xC
3
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
21
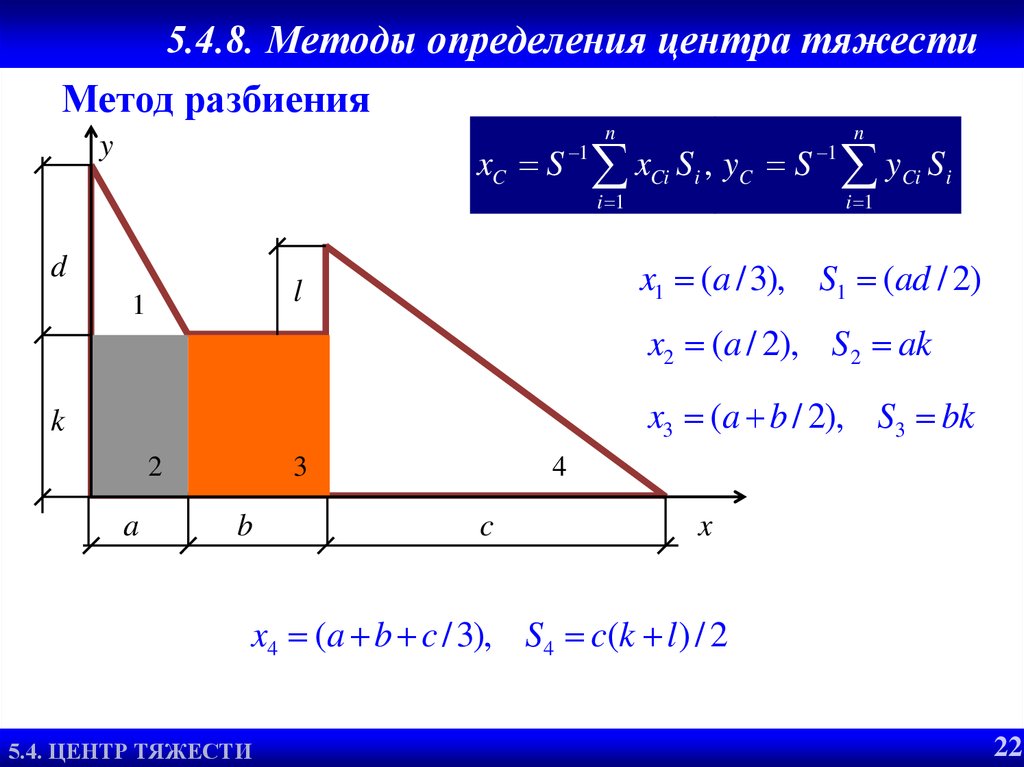
26. 5.4.8. Методы определения центра тяжести
Метод разбиенияn
n
i 1
i 1
xC S 1 xCi Si , yC S 1 yCi S i
y
d
x1 (a / 3), S1 (ad / 2)
l
1
x2 (a / 2), S2 ak
x3 (a b / 2), S3 bk
k
2
a
3
b
4
c
x
x4 (a b c / 3), S4 c(k l ) / 2
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
22
27. 5.4.9. Методы определения центра тяжести
Метод дополнений (отрицательных весов)• Пусть тело, вес которого P, имеет полость заданного объема V. Если бы тело
не имело полости, то его вес был бы равен P’ = P+PV, где PV – вес объема V.
• Радиус-вектор тела без полости тогда равен
'
rc rC P rCV PV / P'
y
для тела с полостью
'
rC rС P' rCV PV / P
Задача 5.2
2
1
xC
x1S1 x2 S 2 a(16 )
S1 S 2
4(8 )
yC
y1S1 y2 S 2 a
S1 S 2
4
a/2
x
a
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
23
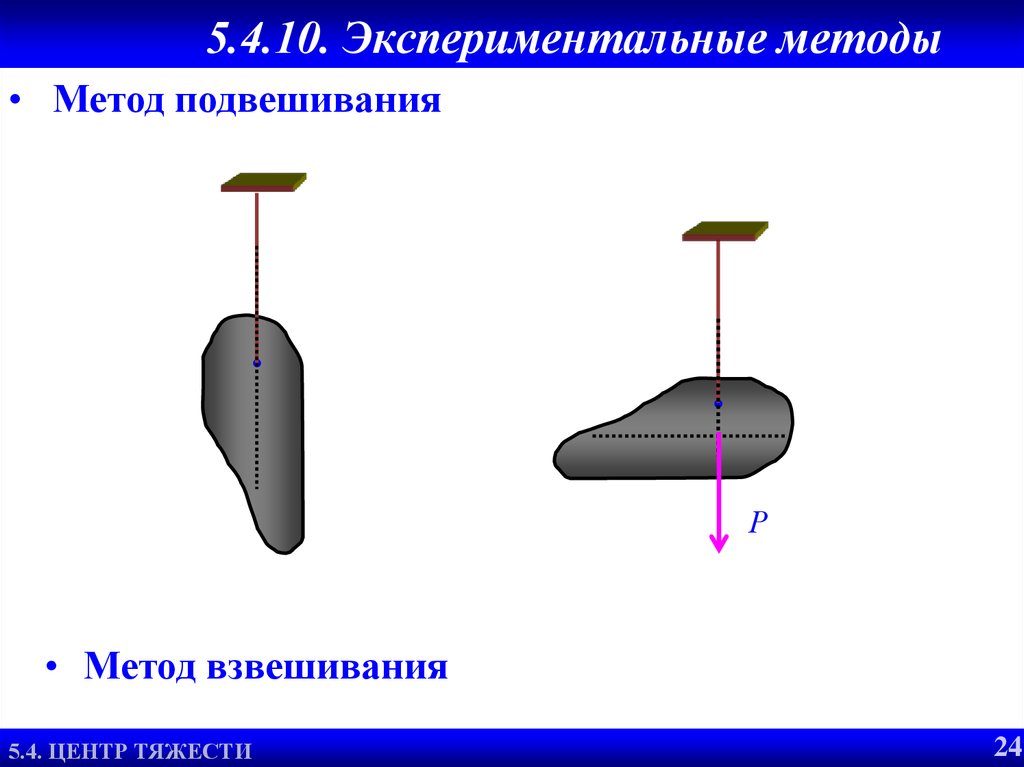
28. 5.4.10. Экспериментальные методы
• Метод подвешиванияР
• Метод взвешивания
2.1.
ССС
5.4. ОПРЕДЕЛЕНИЕ
ЦЕНТР ТЯЖЕСТИ
24
29. 5.5.1. Основные выводы
Наличие силы трения существенно меняет силыреакции связей
Следует различать трение
- покоя
- скольжения
- качения
Сила трения определяется силой нормального
давления данного тела на поверхность
Центр тяжести – это точка приложения
равнодействующей сил тяжести, действующих
на данное тело
5.5.ОСНОВНЫЕ
ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
1.2.
ПОНЯТИЯ И МОДЕЛИ
25
30. 5.5.2. Тема следующей лекции
КОЛЛОКВИУМ1.3.
СТАТИКИ
5.5.
ЗАКЛЮЧЕНИЕ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
26

















 physics
physics








