Тетраэдр. Урок 18

1.

A
Задача 1
Дано:
5 см
A1
A1A2 = 2A1A = 12 см
AB1 = 5 см
Найти: АА2 , АВ2
Решение:
12 см
A2
∆А1АВ1 ∼ ∆А2АВ2
А
B
C
А1
А2
В1
B2

2.

3.

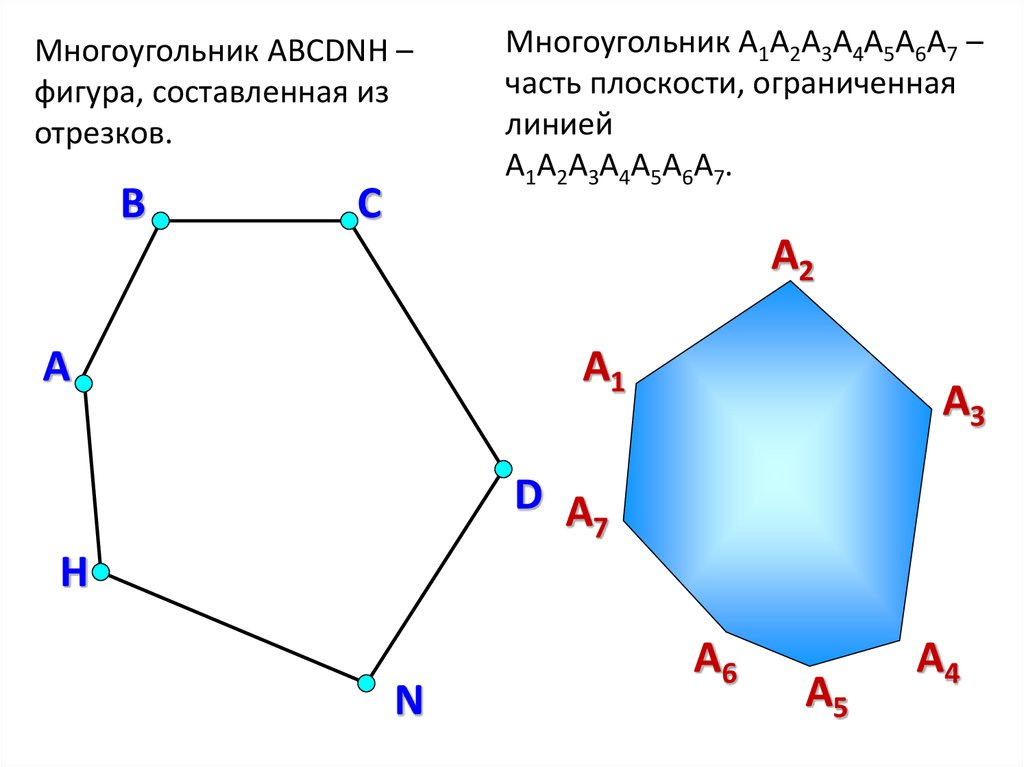
Многоугольник ABCDNH –
фигура, составленная из
отрезков.
В
С
Многоугольник A1А2А3А4А5А6А7 –
часть плоскости, ограниченная
линией
A1А2А3А4А5А6А7.
А2
А
А1
А3
D А
7
H
N
А6
А5
А4

4.

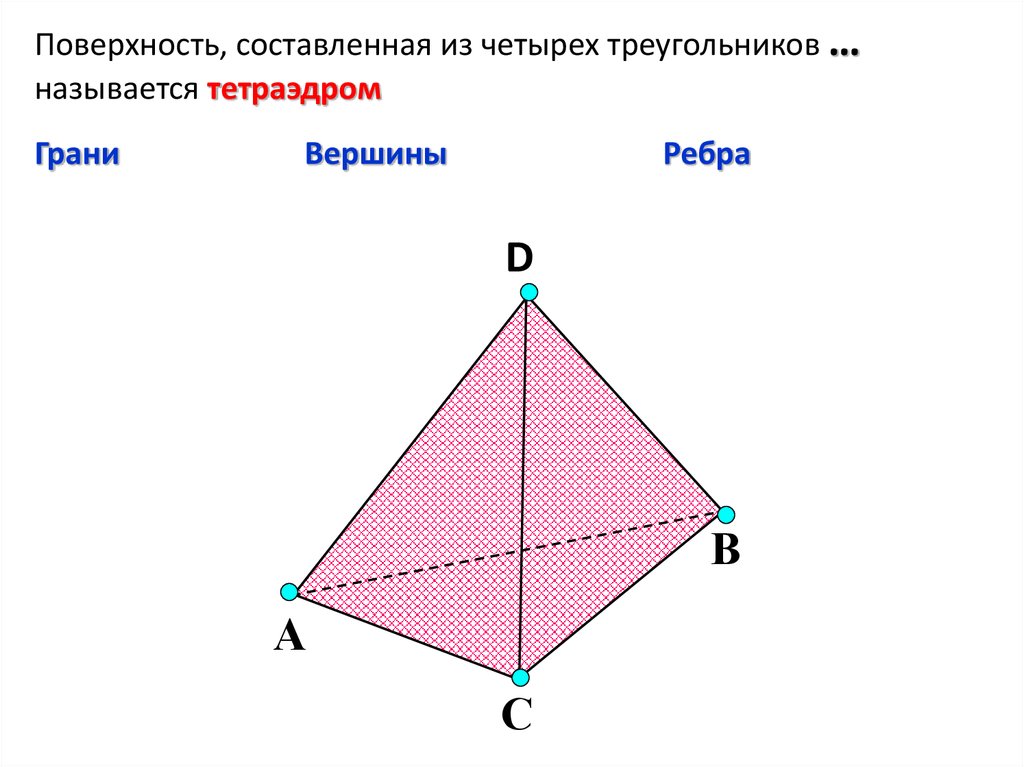
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани
Вершины
Ребра
D
В
А
С

5.

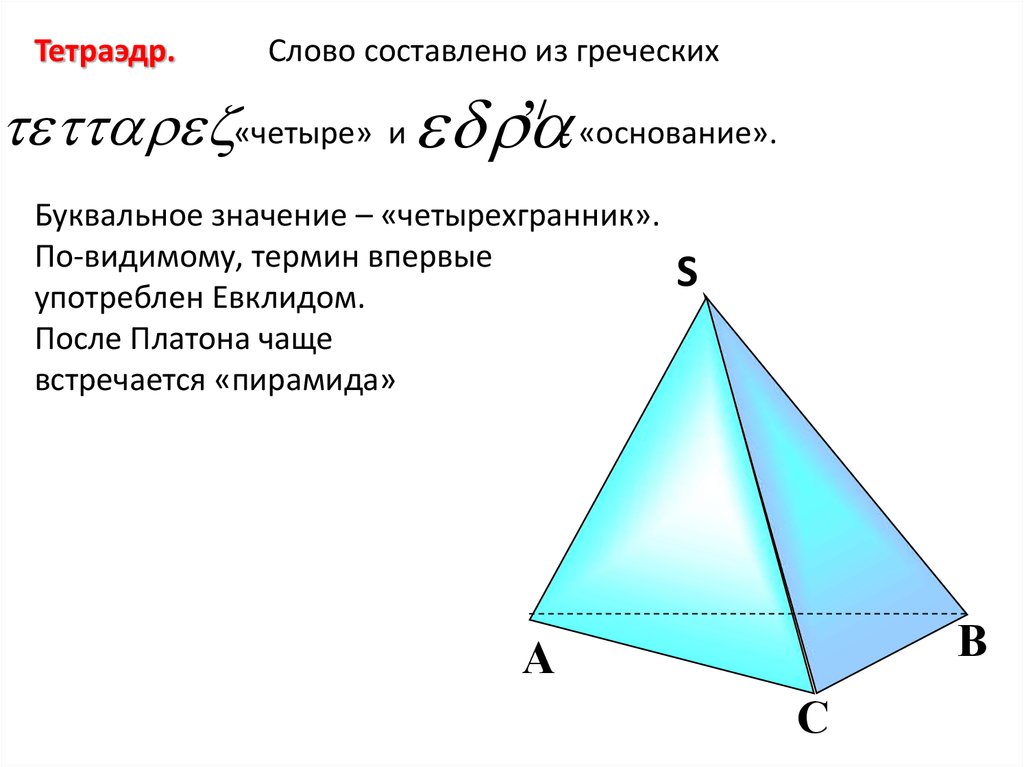
Тетраэдр.
Слово составлено из греческих
«четыре» и - «основание».
,/
Буквальное значение – «четырехгранник».
По-видимому, термин впервые
S
S
употреблен Евклидом.
После Платона чаще
встречается «пирамида»
В
А
С

6.

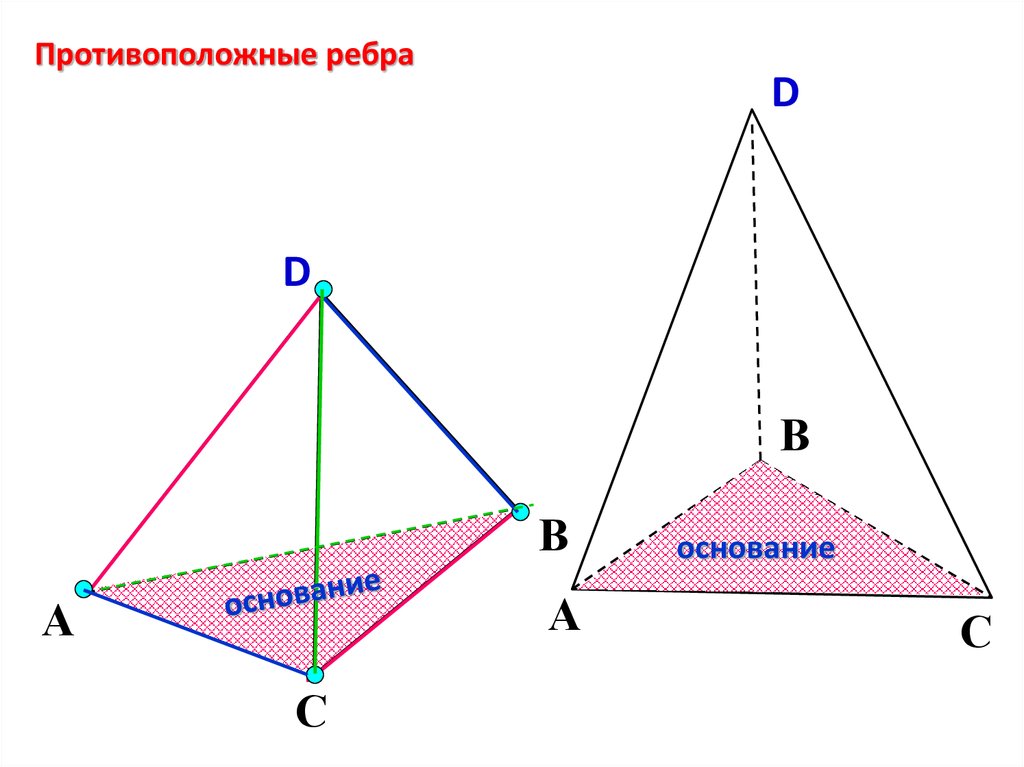
Противоположные ребра
D
D
В
В
А
А
С
основание
С

7.

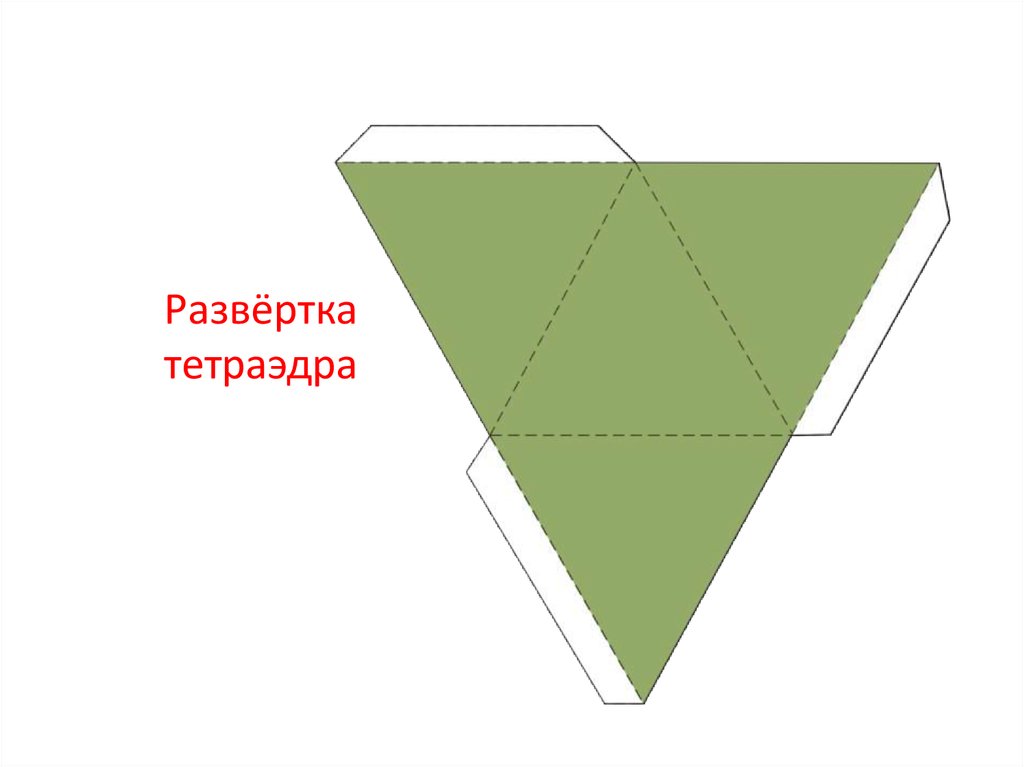
Развёртка
тетраэдра

8.

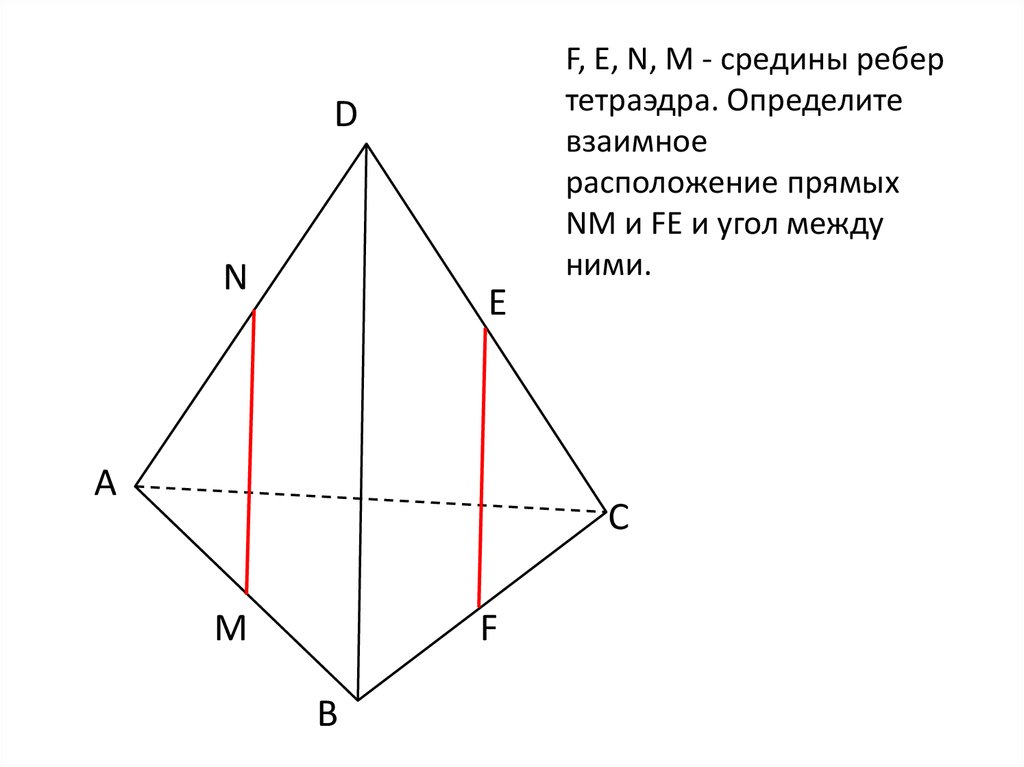
F, Е, N, M - средины ребер
тетраэдра. Определите
взаимное
расположение прямых
NM и FЕ и угол между
ними.
D
N
E
А
С
M
F
В

9.

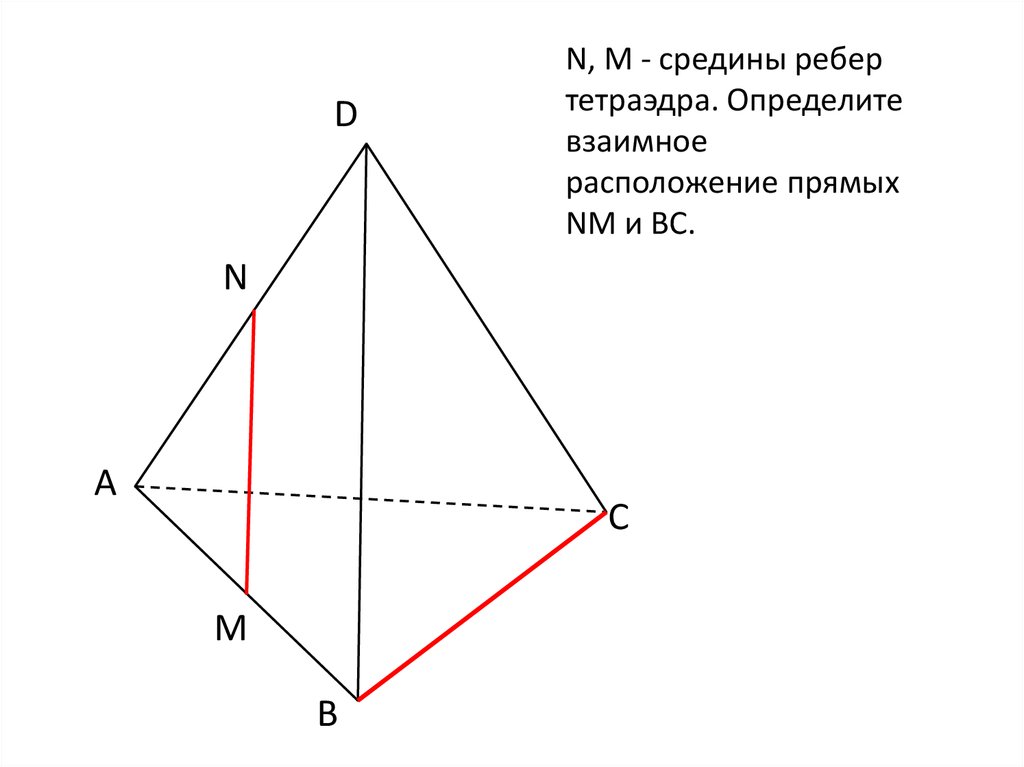
D
N, M - средины ребер
тетраэдра. Определите
взаимное
расположение прямых
NM и ВС.
N
А
С
M
В

10.

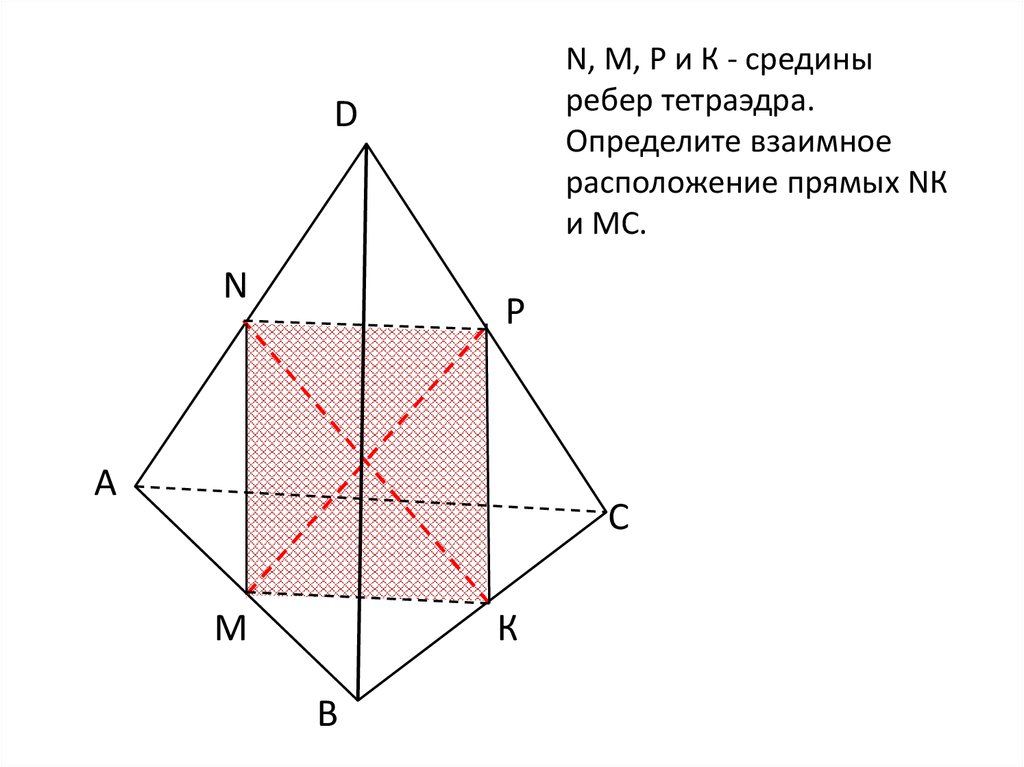
N, M, Р и К - средины
ребер тетраэдра.
Определите взаимное
расположение прямых NК
и МС.
D
N
Р
А
С
M
К
В

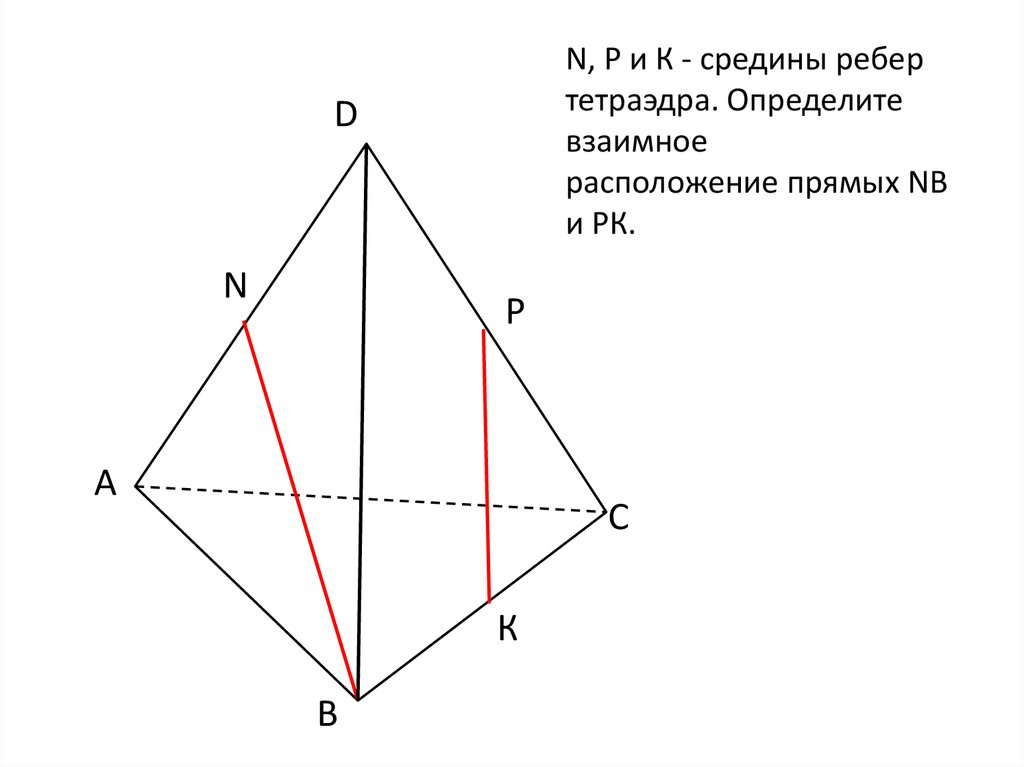
11.

N, Р и К - средины ребер
тетраэдра. Определите
взаимное
расположение прямых NВ
и РК.
D
N
Р
А
С
К
В

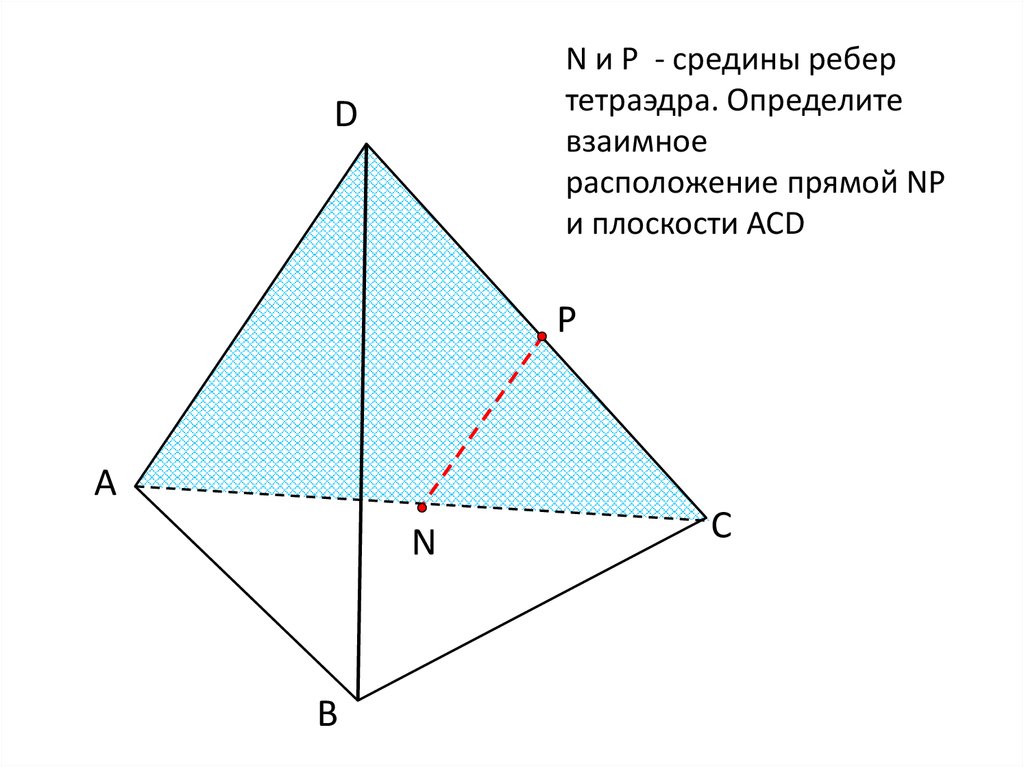
12.

N и Р - средины ребер
тетраэдра. Определите
взаимное
расположение прямой NР
и плоскости АСD
D
Р
А
N
В
С

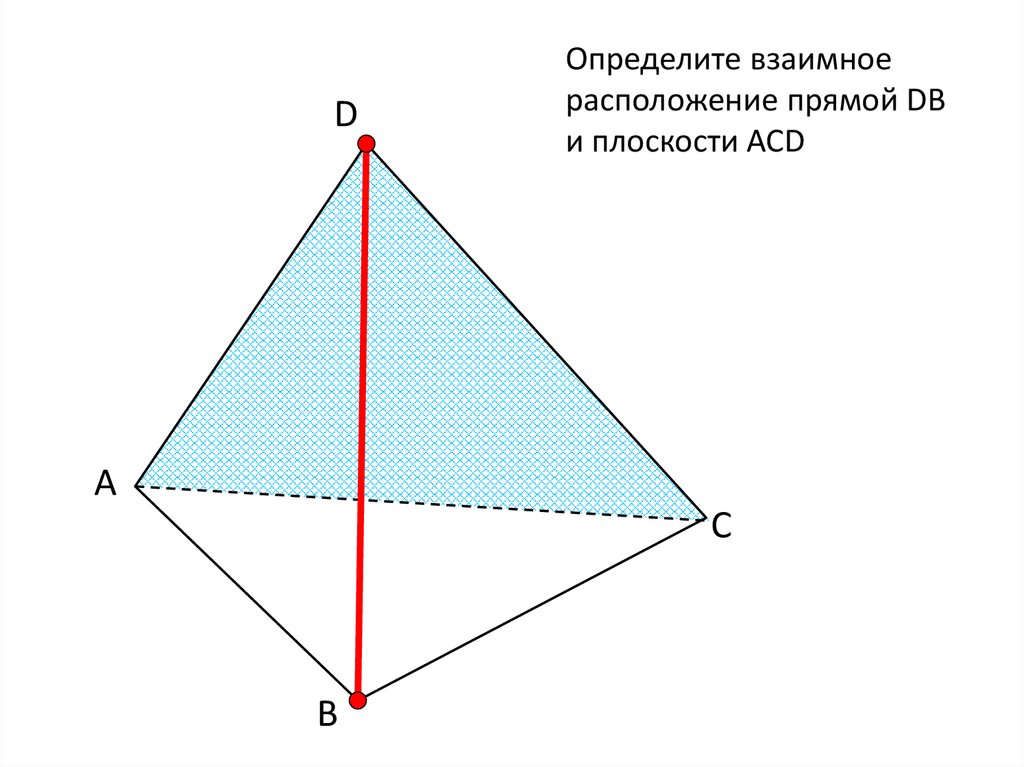
13.

D
Определите взаимное
расположение прямой DВ
и плоскости АСD
А
С
В

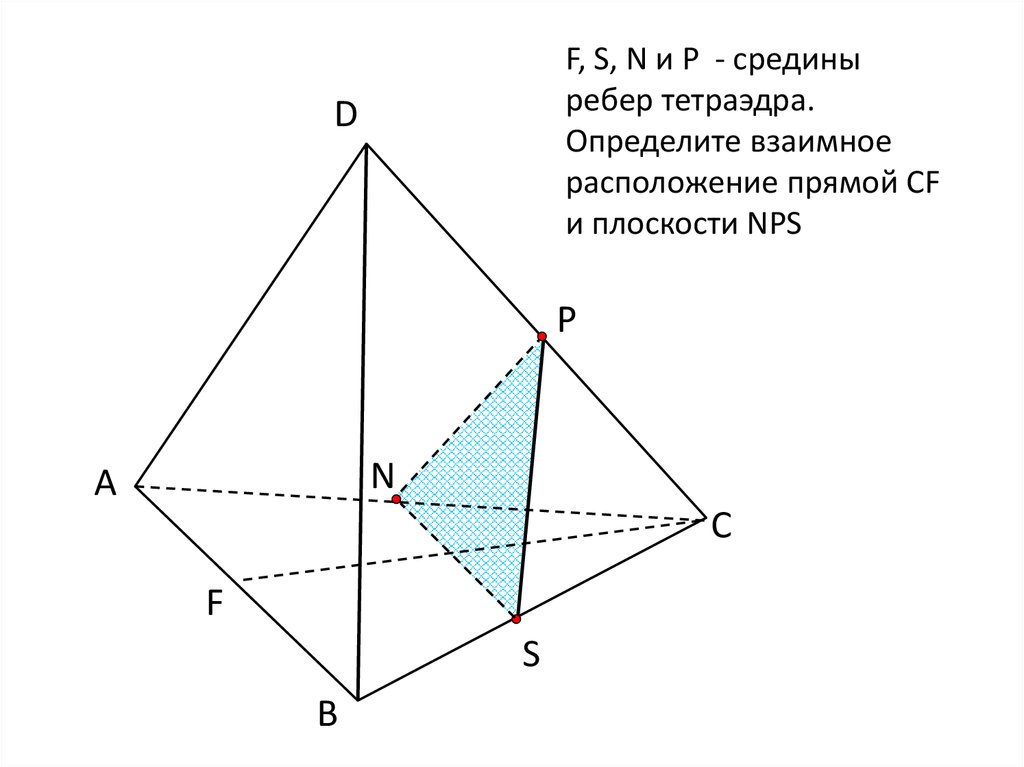
14.

F, S, N и Р - средины
ребер тетраэдра.
Определите взаимное
расположение прямой CF
и плоскости NPS
D
Р
N
А
С
F
S
В

15.

K, F, S, N и Р - средины
ребер тетраэдра.
Определите взаимное
расположение прямой KF
и плоскости NPS
D
Р
K
N
А
С
F
S
В

16.

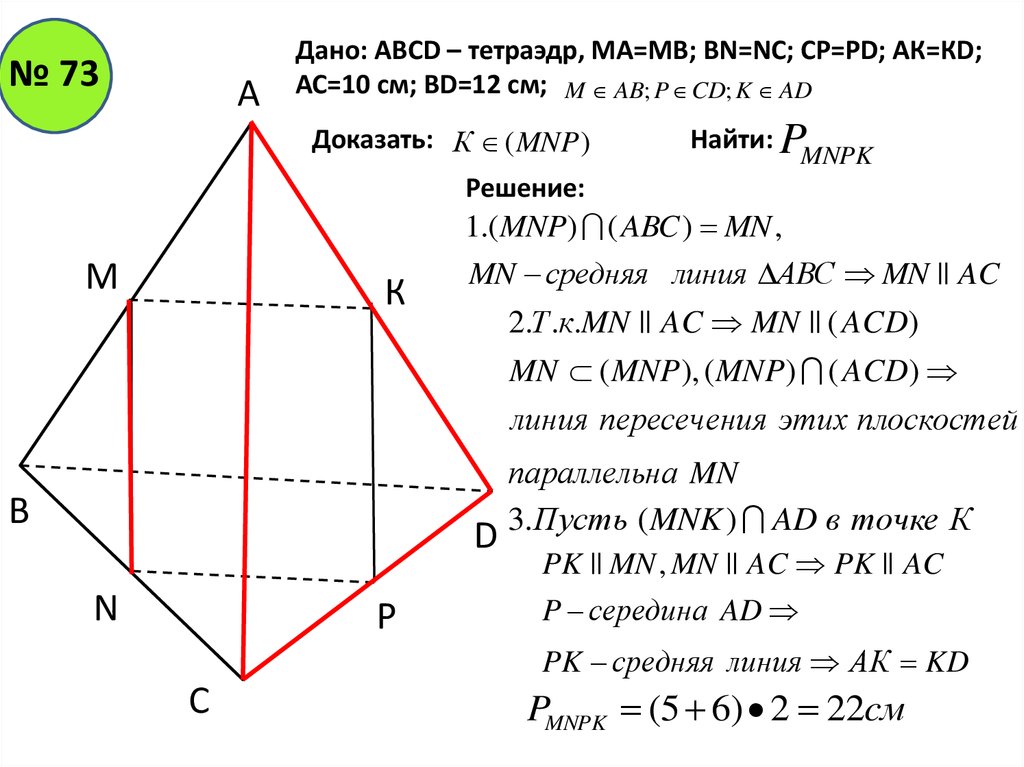
№ 73
А
Дано: АВСD – тетраэдр, МА=МВ; ВN=NC; CP=PD; АК=КD;
АС=10 см; BD=12 см; M AB; P CD; K AD
Доказать: К (MNP )
Найти: P
MNPK
Решение:
1.( MNP) ( ABC ) MN ,
M
К
MN средняя линия АВС MN || AC
2.Т .к.MN || AC MN || ( ACD)
MN ( MNP ), ( MNP ) ( ACD)
линия пересечения этих плоскостей
В
N
Р
параллельн а MN
D 3.Пусть ( MNK ) AD в точке К
PK || MN , MN || AC PK || AC
P середина AD
PK средняя линия АК KD
С
PMNPK (5 6) 2 22cм