Similar presentations:
Построение сечений тетраэдра и параллелепипеда
1.
Кощеев М.М.МКОУ «Погорельская СОШ».
2.
Геометрия является самыммогущественным
средством для изощрения
наших умственных
способностей и дает нам
возможность правильно
мыслить и рассуждать.
Галилео Галилей
3.
ТренажерыПостроение сечений
тетраэдра
1
2 3
4
5
1
2
3
Построение сечений
параллелепипеда
4
5
6
7
8
9
Самостоятельная
работа
«3»
Основные
правила
«4»
«5»
проверка
10
11
Дополнительное
задание
1
2
4.
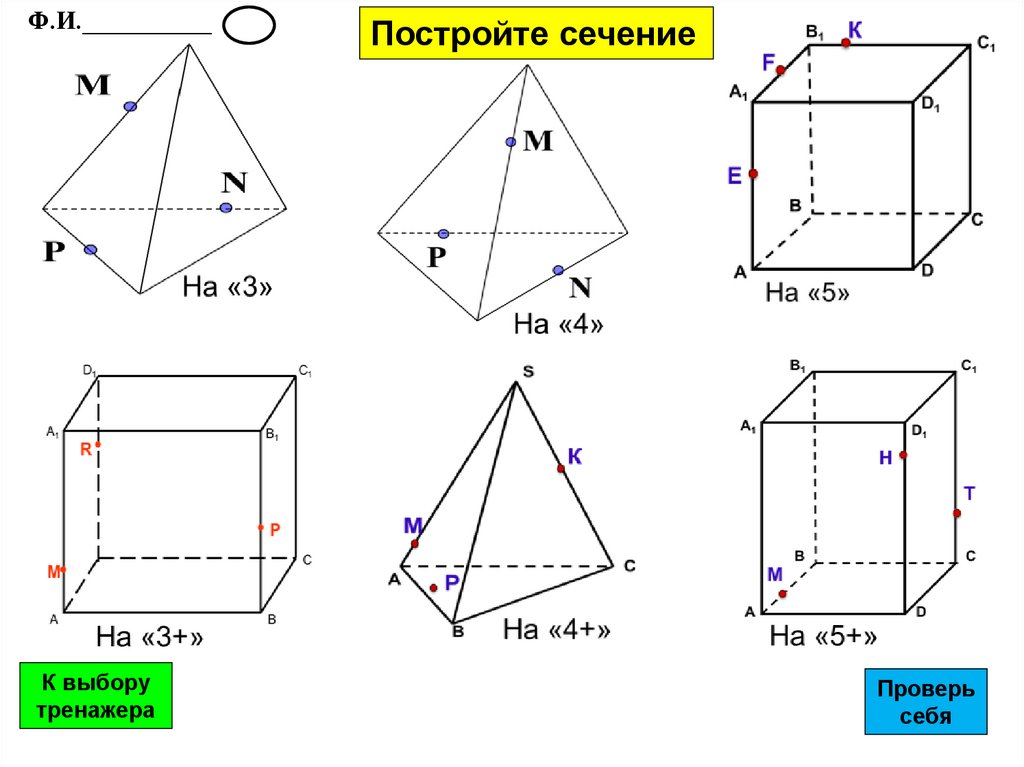
Ф.И.__________К выбору
тренажера
Постройте сечение
Проверь
себя
5.
Практические примеры №1Построить сечение тетраэдра через ребро KL и середину
ребра А ребра MN.
K
KLA LMN LA
KLA KNM KA
M
L
К выбору
тренажера
A
N
Основные
правила
6.
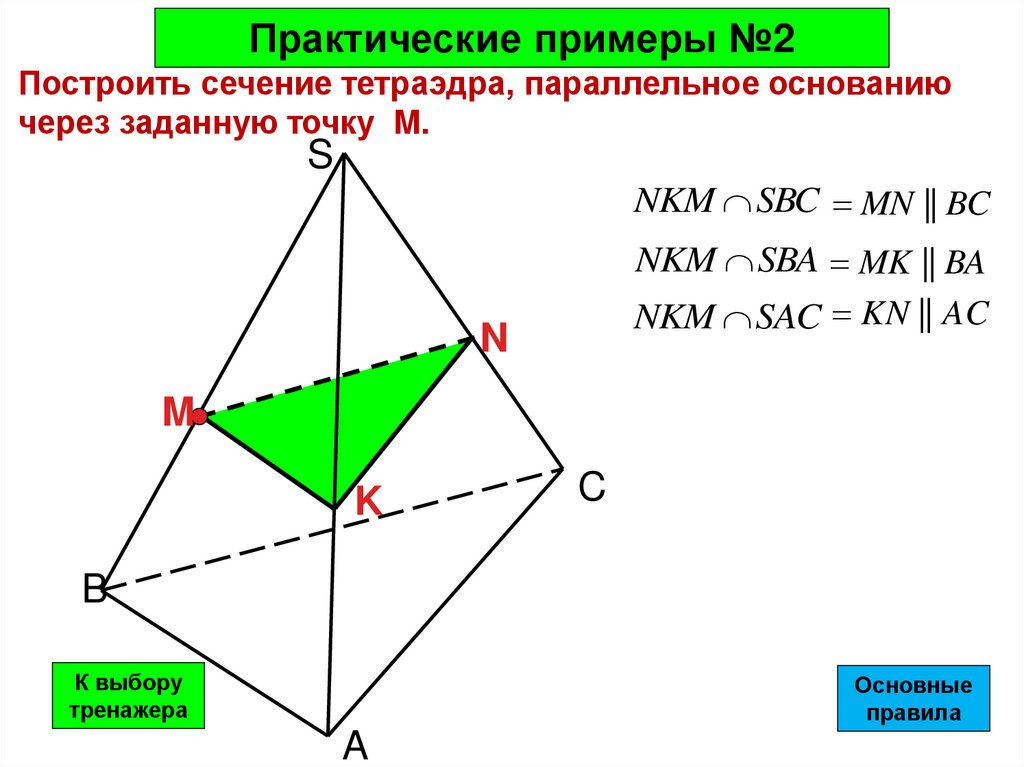
Практические примеры №2Построить сечение тетраэдра, параллельное основанию
через заданную точку M.
S
NKM SBC MN || BC
NKM SBA MK || BA
NKM SAC KN || AC
N
M
K
C
B
К выбору
тренажера
Основные
правила
A
7.
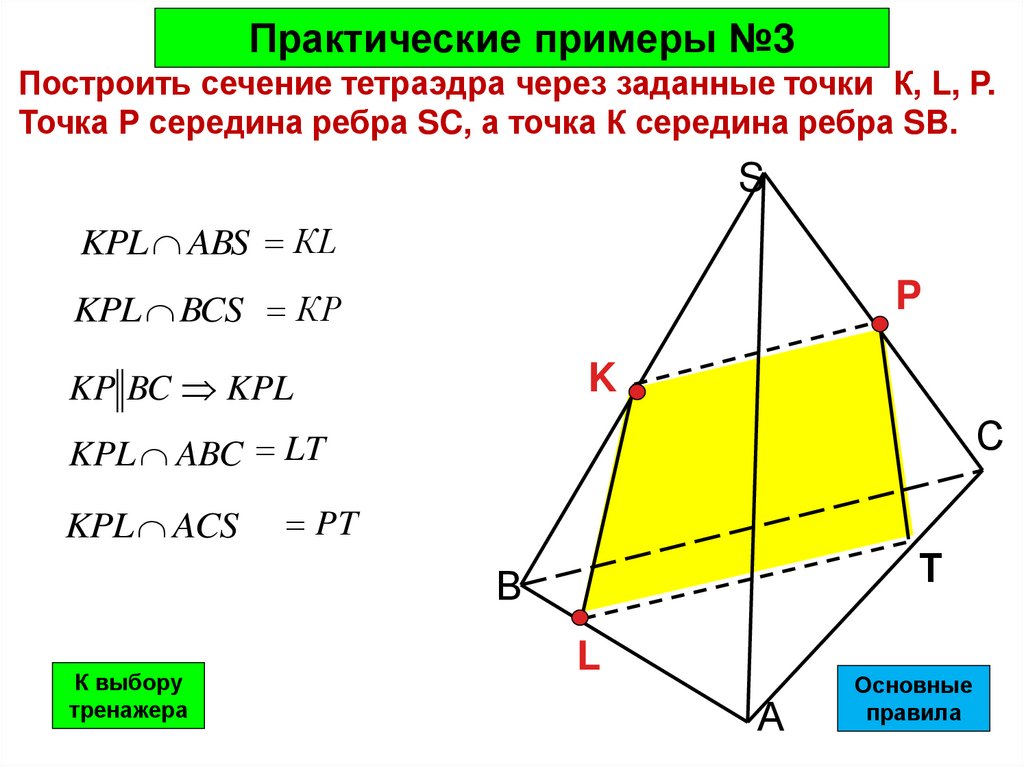
Практические примеры №3Построить сечение тетраэдра через заданные точки К, L, P.
Точка Р середина ребра SC, а точка К середина ребра SB.
S
KPL ABS КL
P
KPL BCS КP
K
KP BC KPL
С
KPL ABC LT
KPL ACS
PT
Т
В
К выбору
тренажера
L
А
Основные
правила
8.
Практические примеры №4Построить сечение тетраэдра через заданные точки N, K, M.
Воспользуемся правилами построения
сечений.
S
Найдем отрезки, по которым секущая
плоскость NKM пересекает каждую
грань.
М
NKM SBC КМ
К
NKM SBA КN
С
NKM BAC NT
NKM SAC МT
К выбору
тренажера
В
Т
N
А
Основные
правила
9.
Практические примеры №5Построить сечение тетраэдра плоскостью МNК через точки
М и N лежащих на ребрах DB и DC и внутреннюю точку К
грани АВС .
D
NKM DCB NМ
NKM ABC PF
M
NKM DAC PN
NKM DAB FM
B
F
A
K
N
P
К выбору
тренажера
C
Основные
правила
10.
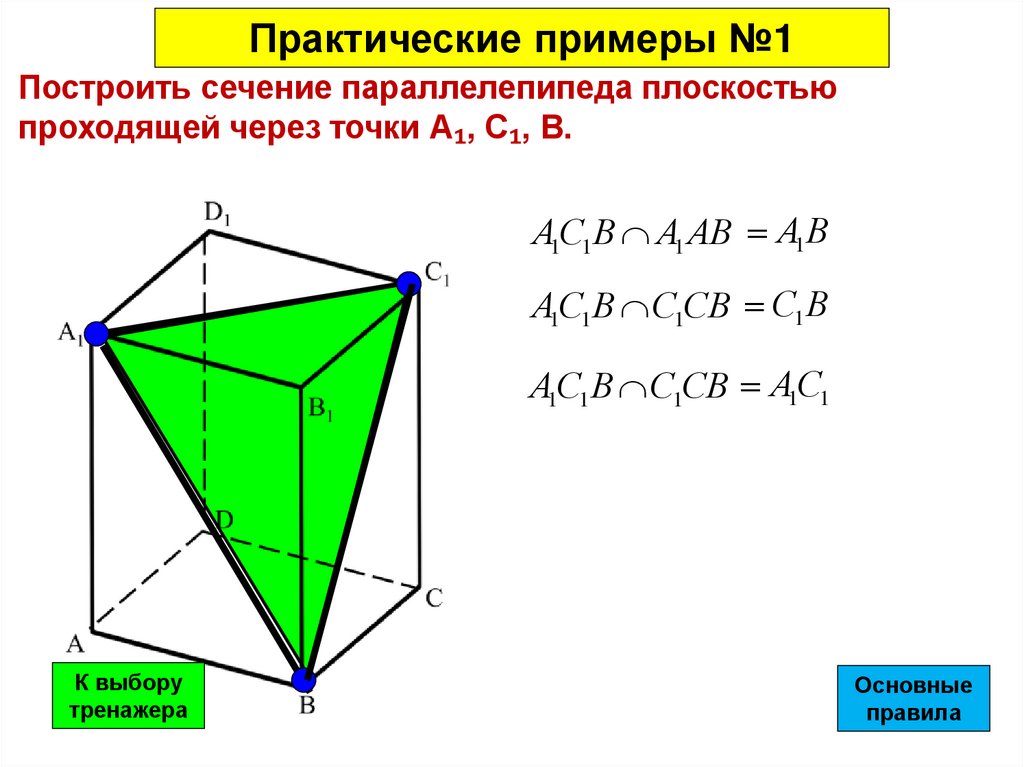
Практические примеры №1Построить сечение параллелепипеда плоскостью
проходящей через точки А₁, С₁, В.
А1С1В А1 АВ А1В
А1С1В С1СВ С1В
А1С1В С1СВ А1С1
К выбору
тренажера
Основные
правила
11.
Практические примеры №2Построить сечение параллелепипеда плоскостью
проходящей через точки К, M, N.
KMN А1 АВ KN
M
KMN С1СВ MN
KNM А1С1В1 KM
K
N
К выбору
тренажера
Основные
правила
12.
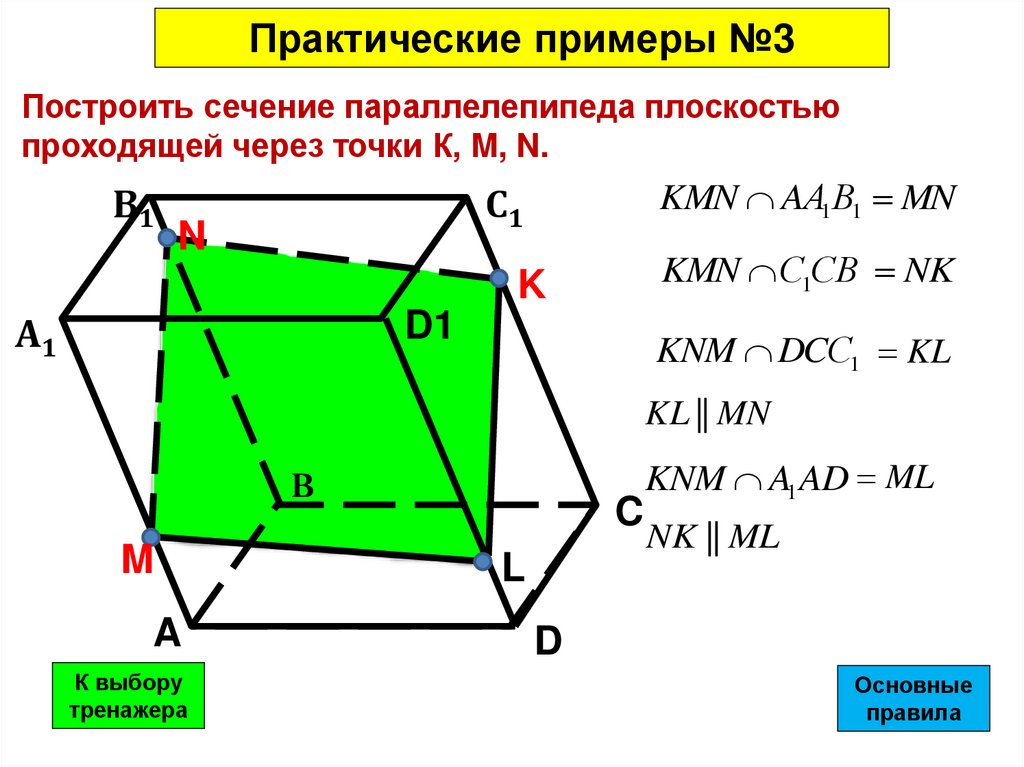
Практические примеры №3Построить сечение параллелепипеда плоскостью
проходящей через точки К, M, N.
В1
N
А1
С1
KMN AА1В1 MN
K
KMN С1СВ NK
D1
KNM DCС1 KL
KL || MN
B
M
A
К выбору
тренажера
C
L
KNM A1 AD ML
NK || ML
D
Основные
правила
13.
Практические примеры №4Построить сечение параллелепипеда плоскостью
проходящей через точки M, N, K.
MNK AА1В1 MN
MNK С1CD KL
L
MN || KL
KMN ADD1 LM
KMN BCC1 KP
KP || ML
P
К выбору
тренажера
KMN ABC PN
Основные
правила
14.
Практические примеры №5Построить сечение параллелепипеда плоскостью
проходящей через точки А, D₁, P.
AD1P AA1D1 AD1
AD1P ABC AP
AD1P DCC1 D1L
L
AD1P BCC1 PL
K
К выбору
тренажера
Основные
правила
15.
Практические примеры №6На гранях куба заданы точки K, L, M. Требуется построить
сечение куба плоскостью, проходящей через заданные точки.
KLM BCC1 KM
KLM ABC LN
R
KLM ABB1 NM
KLM DCC1 RK
MN || RK
К выбору
тренажера
N
Т
KLM ADD1
LR
LR || MK
Основные
правила
16.
Практические примеры №7Постройте сечение параллелепипеда проходящее через
точки N, Р, и М.
MNP ABC PN
В1
М
С1
Т
А1
D1
В
MNP ABB1 HM
MNP ABC
О
HP
MNP A1B1C1 MT
N
С
MNP DCC1 NT
АН
Е
К выбору
тренажера
Р
D
Основные
правила
17.
Практические примеры №8Постройте сечение параллелепипеда проходящее через
точки N, Р, и М.
MNP A1B1C1 MN
Е
В1
С1
N
М
Р
А1
D1
L
К
В
С
F
S
А
К выбору
тренажера
D
MNP BCC1 NP
MNP ABB1 ML
MNP ABC SF
О
MNP DCC1 FP
MNP ABB1 SL
Основные
правила
18.
Практические примеры №9Построить сечение
параллелепипеда плоскостью
проходящей через точки T, P, O.
В1
TOP AА1В1 TP
TPO С1СВ TO
С1
TPO ADC LF
T
А1
TPO A1 AD LP
D1
TPO DCC1 FO
O
B
C
M
P
К выбору
тренажера
A
N
F
L
D
Основные
правила
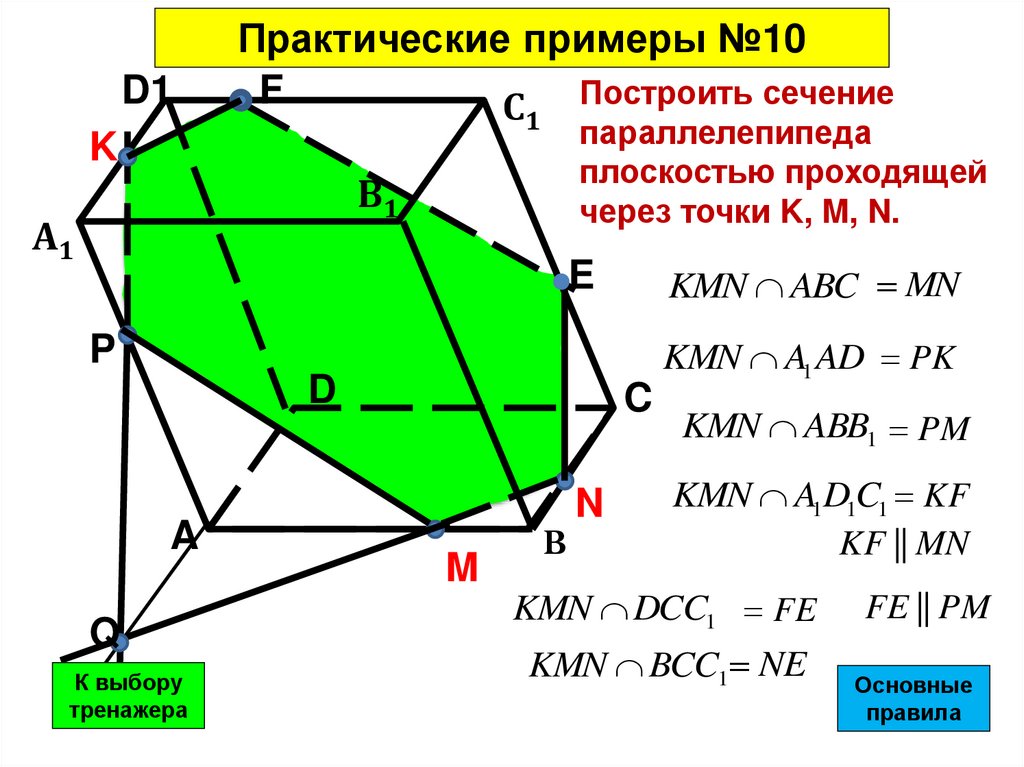
19.
D1Практические примеры №10
F
С Построить сечение
1
K
параллелепипеда
плоскостью проходящей
через точки K, M, N.
В1
А1
KMN ABC MN
E
P
D
A
Q
К выбору
тренажера
C
M
B
N
KMN A1 AD PK
KMN ABB1 PM
KMN A1D1C1 KF
KF || MN
KMN DCC1 FE
KMN BCC1 NE
FE || PM
Основные
правила
20.
Практические примеры №11Постройте сечение параллелепипеда проходящее через
точки М, N, и L.
MNL BCC1 MN
Q
В1
Т
М
А1
С1
N
D1
В
С
L
А R
Е
К выбору
тренажера
Н
MNL DCC1 NL
MNL ADC LH
MNL ABB1 RT
MNL A1 B1C TM
К
MNL ABC RH
D
Основные
правила
21.
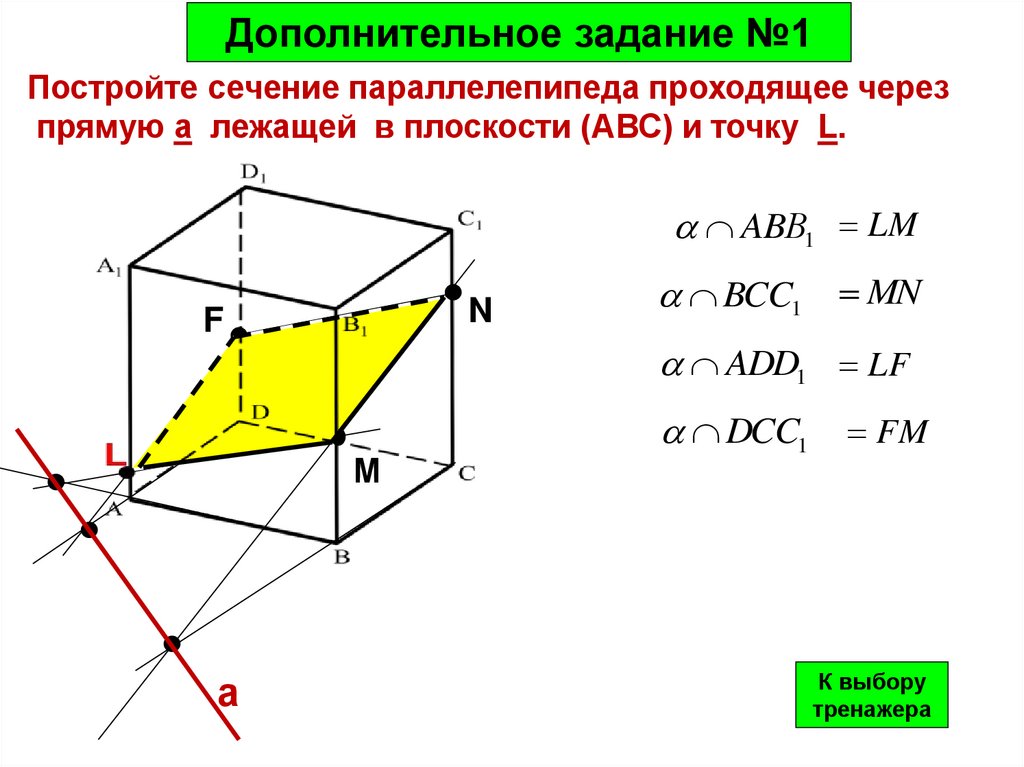
Дополнительное задание №1Постройте сечение параллелепипеда проходящее через
прямую а лежащей в плоскости (АВС) и точку L.
ABВ1 LM
N
F
ADD1 LF
М
а
BCC1 MN
DCC1
FM
К выбору
тренажера
22.
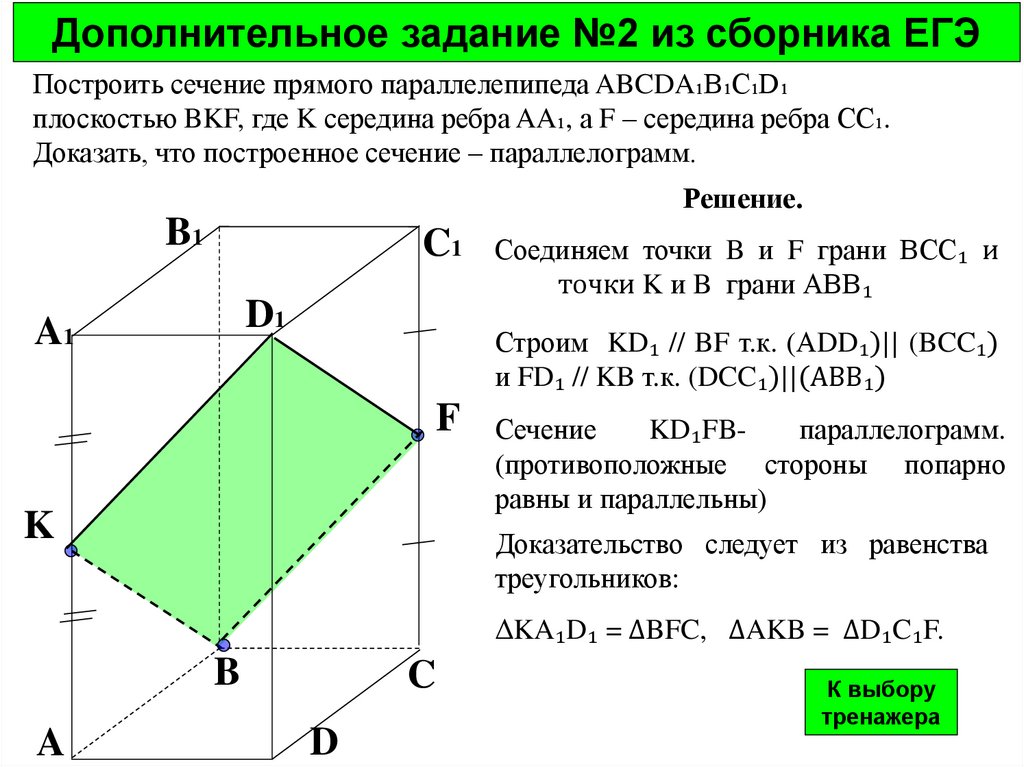
Дополнительное задание №2 из сборника ЕГЭПостроить сечение прямого параллелепипеда ABCDA₁В₁С₁D₁
плоскостью BKF, где K середина ребра AA₁, а F – середина ребра СС₁.
Доказать, что построенное сечение – параллелограмм.
Решение.
B1
C1
D1
A1
Соединяем точки B и F грани ВСС₁ и
точки K и B грани АВВ₁
Строим KD₁ // BF т.к. (АDD₁)|| (BCC₁)
и FD₁ // KB т.к. (DCC₁)||(АВВ₁)
F
K
Сечение
KD₁FBпараллелограмм.
(противоположные стороны попарно
равны и параллельны)
Доказательство следует из равенства
треугольников:
ΔKA₁D₁ = ΔBFC, ΔAKB = ΔD₁C₁F.
B
A
C
D
К выбору
тренажера














 mathematics
mathematics








