Similar presentations:
Сечение многогранников: параллелепипеда и тетраэдра (урок геометрии)
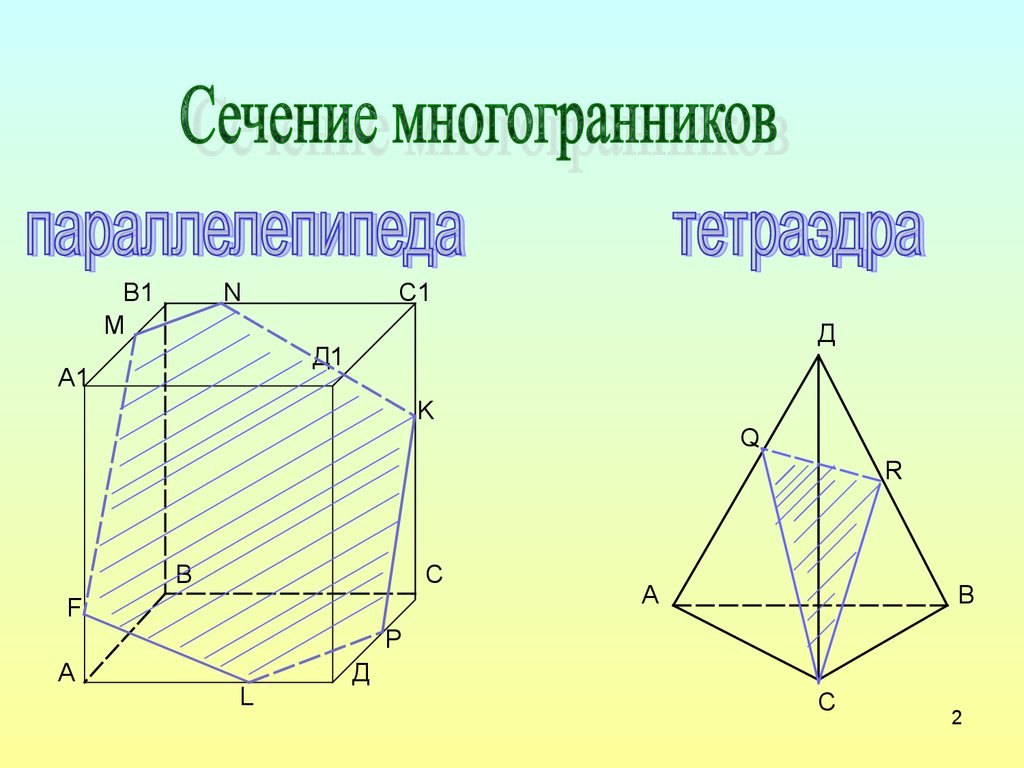
1.
12.
В1M
N
С1
Д
Д1
А1
K
Q
R
В
С
F
А
В
P
А
L
Д
С
2
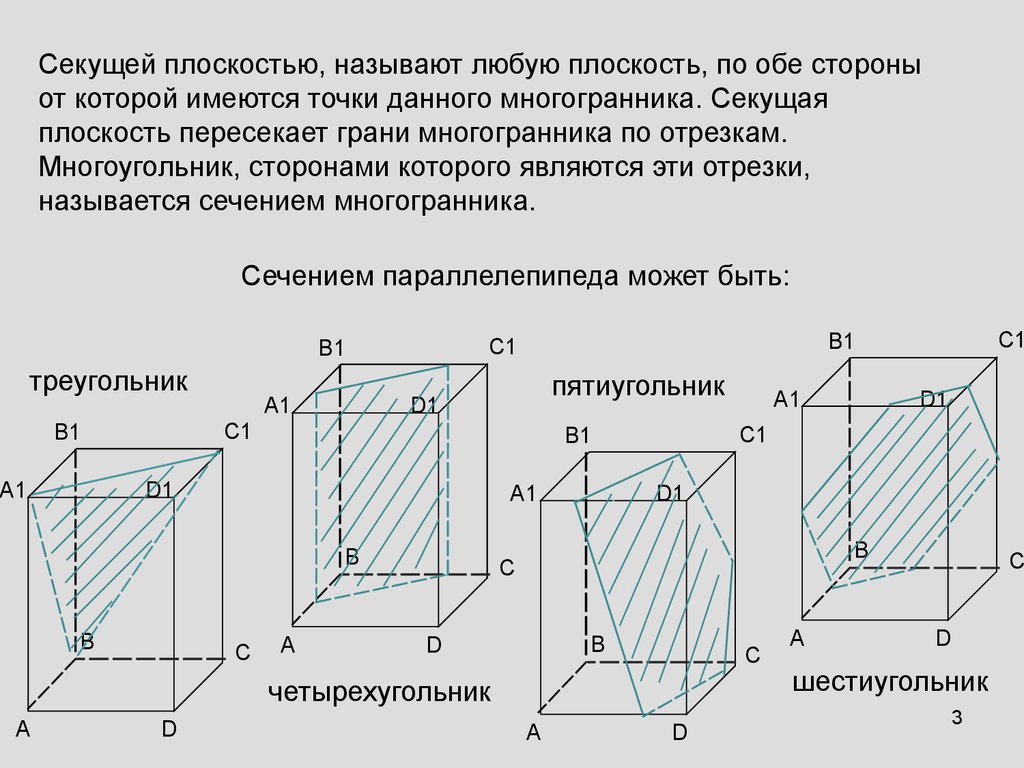
3.
Секущей плоскостью, называют любую плоскость, по обе стороныот которой имеются точки данного многогранника. Секущая
плоскость пересекает грани многогранника по отрезкам.
Многоугольник, сторонами которого являются эти отрезки,
называется сечением многогранника.
Сечением параллелепипеда может быть:
треугольник
пятиугольник
D1
С1
В1
А1
А1
А1
В
В
С
А
D
D1
D1
В
С
В
D
С
четырехугольник
А
А1
С1
В1
D1
С1
В1
С1
В1
А
D
А
С
D
шестиугольник
3
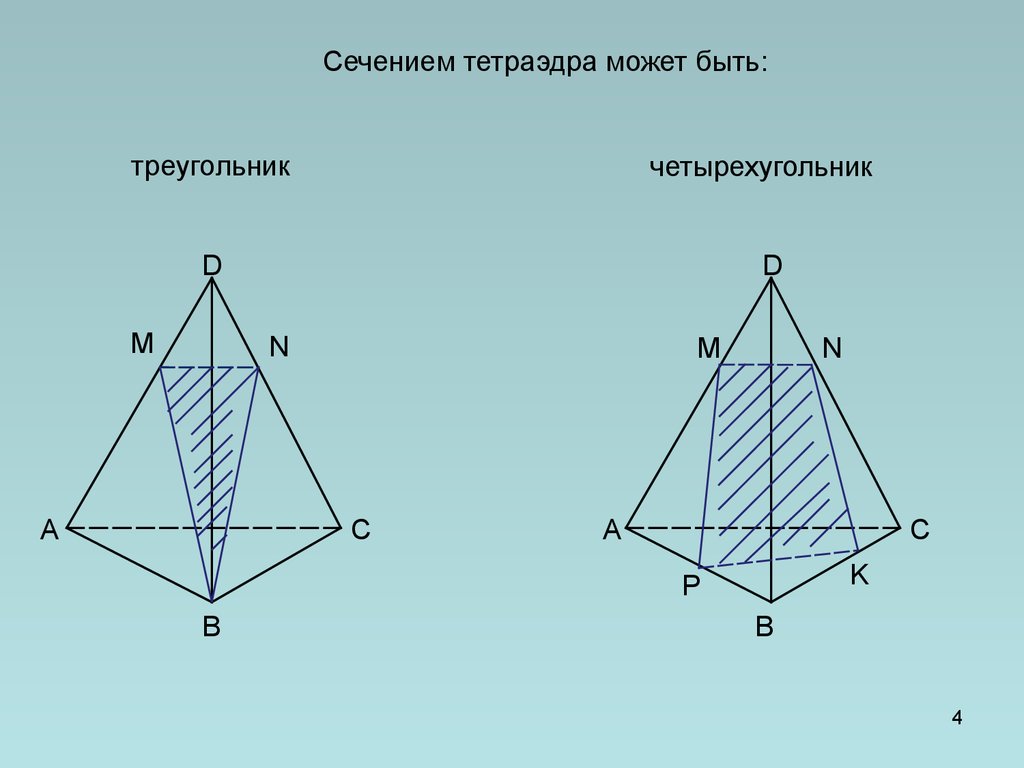
4. Сечением тетраэдра может быть:
треугольникчетырехугольник
D
М
D
N
А
M
С
N
А
С
K
P
В
В
4
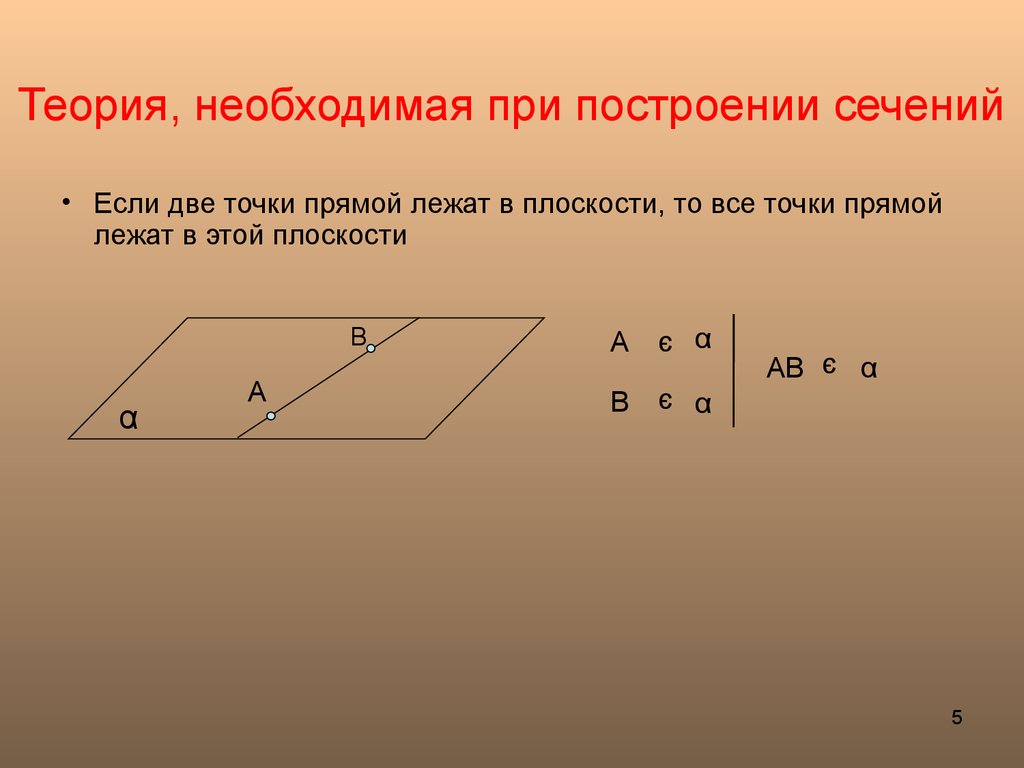
5. Теория, необходимая при построении сечений
• Если две точки прямой лежат в плоскости, то все точки прямойлежат в этой плоскости
В
α
А
A
є α
B
є α
AB є α
5
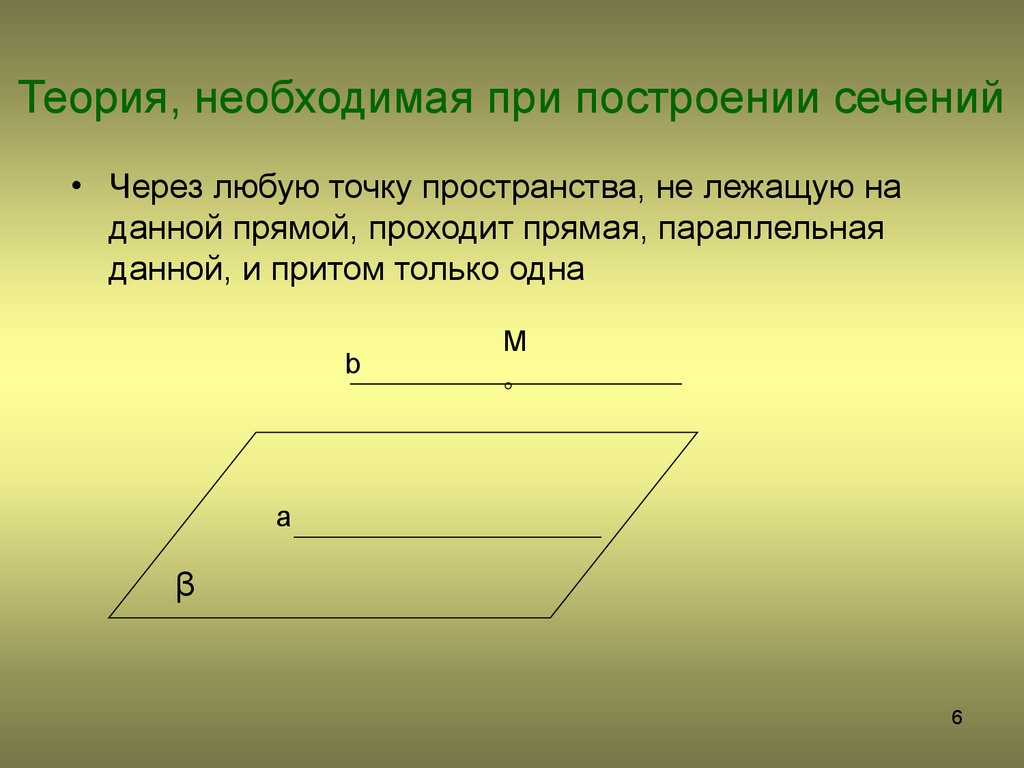
6. Теория, необходимая при построении сечений
• Через любую точку пространства, не лежащую наданной прямой, проходит прямая, параллельная
данной, и притом только одна
b
М
◦
а
β
6
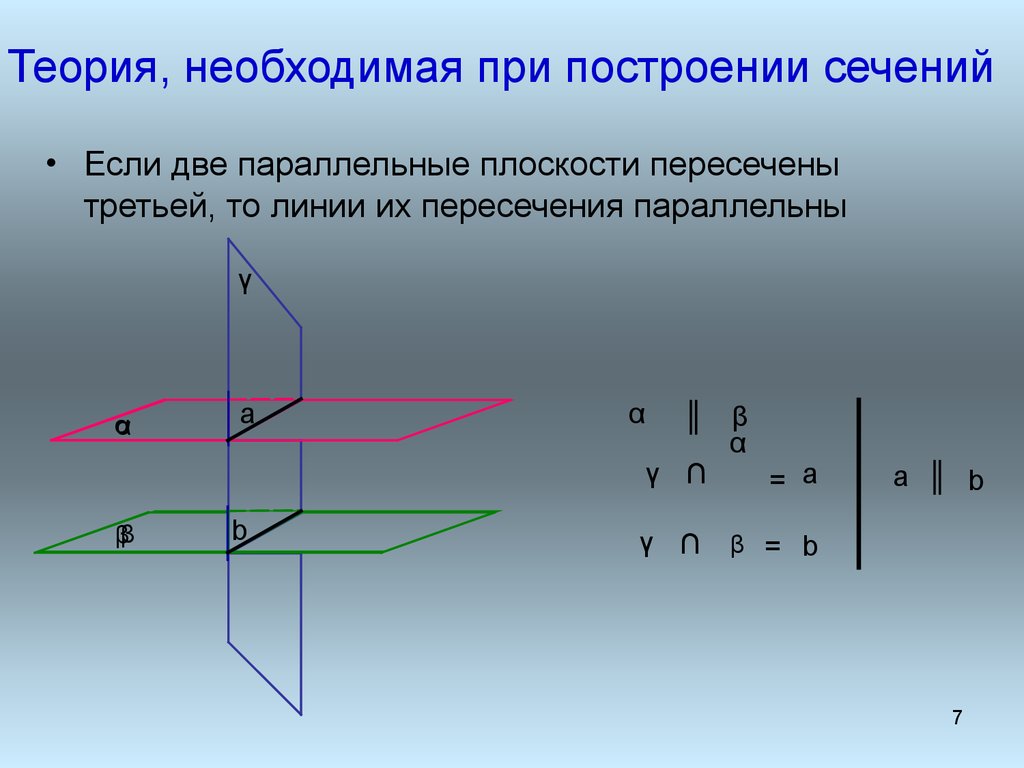
7. Теория, необходимая при построении сечений
• Если две параллельные плоскости пересеченытретьей, то линии их пересечения параллельны
γ
α
ββ
a
b
α
║ β
α
γ ∩
= a
γ ∩
a ║ b
β = b
7
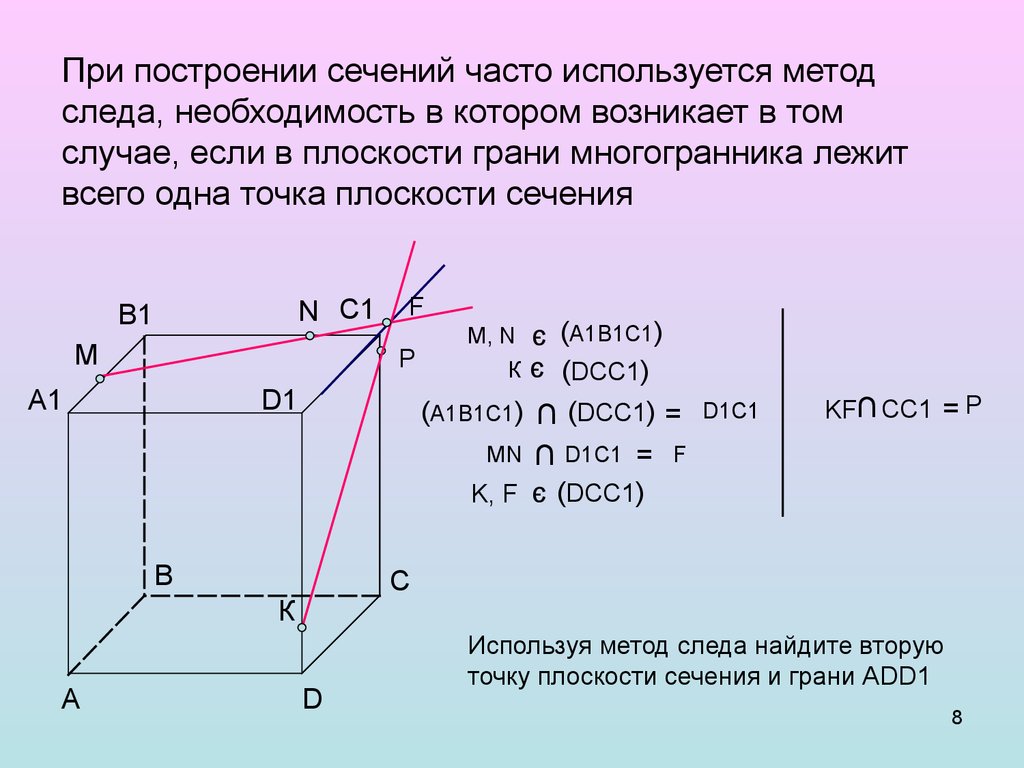
8. При построении сечений часто используется метод следа, необходимость в котором возникает в том случае, если в плоскости грани многогранни
При построении сечений часто используется методследа, необходимость в котором возникает в том
случае, если в плоскости грани многогранника лежит
всего одна точка плоскости сечения
N С1
В1
М
А1
D1
F
є (А1В1С1)
P
К є (DCC1)
(А1В1С1) ∩ (DCC1) =
М, N
∩ D1C1 =
K, F є (DCC1)
МN
В
KF∩ CC1 = P
F
С
К
А
D1C1
D
Используя метод следа найдите вторую
точку плоскости сечения и грани АDD1
8
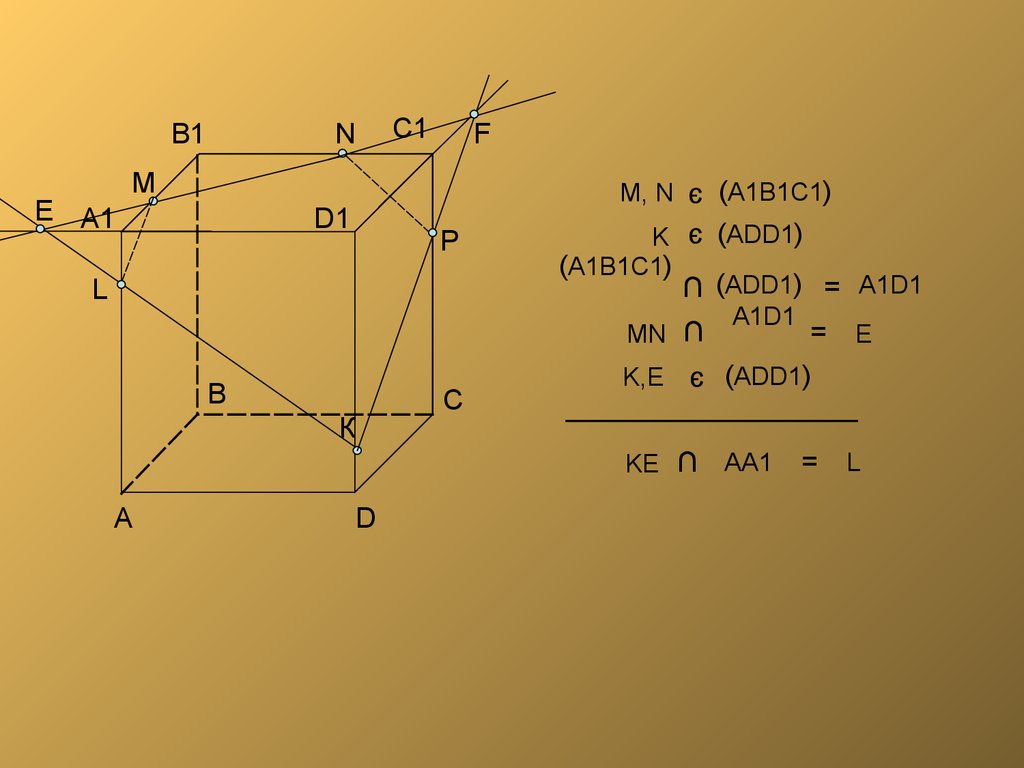
9.
В1E А1
N
С1
F
М
M, N є (A1B1C1)
D1
P
L
В
К
С
K є (ADD1)
(A1B1C1)
∩ (ADD1) = A1D1
A1D1
= E
MN ∩
K,E є (ADD1)
KE ∩
А
D
AA1
=
L
10.
(α-плоскость сечения)N С1
В1
М
А1
F
P
D1
α ∩ (CDD1) = KP
α ∩ (ABB1) = ML
L
В
С
К
А
(CDD1) ║ (ABB1)
D
KP ║ ML
11.
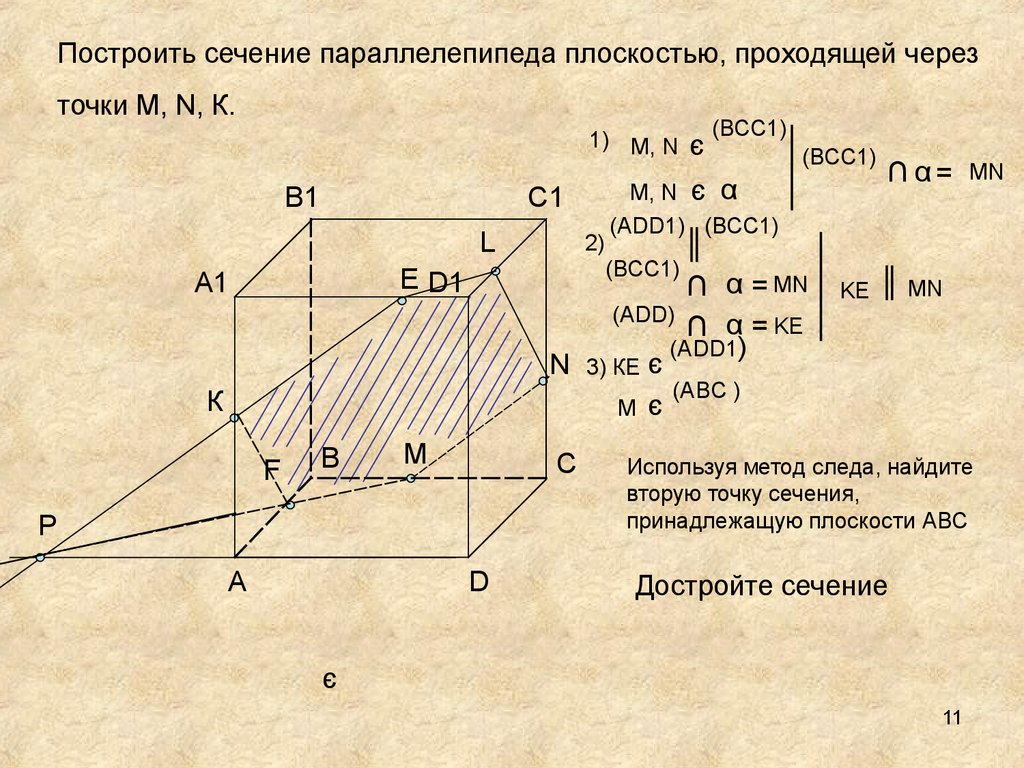
Построить сечение параллелепипеда плоскостью, проходящей черезточки М, N, К.
1) М, N
В1
С1
L
E D1
А1
К
F
В
М
А
D
(ВСС1)
М, N є α
(ADD1) (ВСС1)
║
(ВСС1)
∩ α = MN
(ADD)
∩ α = KE
(ADD1)
N 3) КЕ є
(ABC )
є
M
2)
С
P
є
(ВСС1)
KE
∩ α=
МN
║ MN
Используя метод следа, найдите
вторую точку сечения,
принадлежащую плоскости АВС
Достройте сечение
є
11
12.
Построить сечение тетраэдра плоскостью α , проходящей черезточки М, N, К.
1)
D
M
2)
N
А
В
K
С
(ABD)
є
M, N
(ABD)
M, N
є
M,K
є
(АСD)
M,K
є
α
3) K,N
K,N
є
є
α
(АСD)
∩ α = MN
∩ α = MK
(BCD)
(BCD)
α
∩ α = KN
4) (MNK) – плоскость сечения α
12
13.
Построить сечение тетраэдра плоскостью α , проходящей через точкиМ, N, К.
1)
D
є
є
М
N
2) М
K
M
є
є
(ABD)
( АСD)
( АСD)
K
(ABD)
MK
є
( АСD)
3) М, N є (ABD)
K є (ABC)
(ABD) ∩ (ABC) = AB
МN ∩ AB = L
R
С
K, L
N
є
L
В
R
MN
N
А
4)
(ABD)
є
є
(BCD)
(BCD)
RN
є
(BCD)
5)
є
KL ∩ BC = R
(ABC)
(MNRK) – искомая плоскость α
13




 mathematics
mathematics








