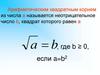Иррациональные уравнения

1.

2.

Равносильны ли следующие уравнения?
5х+10=0 и х+2=0,
Х2 =25 и х=5
Установить, какое из двух уравнений является
следствием другого?
х=-3 и х2=9
Х-5=0 и х(х-5)=0

3. Возведите во вторую степень данные выражения:

• (3х+7)
(2х-5)
9 х 42 х 49
2
4 х 20 х 25
2

4.

Что общего в этих уравнениях?
у+
у 9 =2
2
х 1= х-1
5 х 4 =2 + х

5. Иррациональное уравнения- это уравнения, в которых неизвестное находится под знаком корня.

Иррациональное
уравненияэто уравнения, в
которых неизвестное
находится под
знаком корня.

6. Свойство: При возведении обеих частей уравнения в натуральную степень получается уравнение-следствие данного.

7.

Повторим, что такое уравнение-следствие?
Если при переходе от одного уравнения к
другому потери корней не происходит, то
второе уравнение называют следствием
первого уравнения.
При решении иррациональных
уравнений возведением его в
натуральную степень необходимо
делать проверку

8.

Пример. 1)Решить уравнение:
x 2 5
Решение:
Х+2=52, т.е. х=25-2.
Ответ : х=23

9. II. Решение уравнений вида

f ( x) g ( x )
x 5 2х 3
Решать это уравнение будем
возведением обеих частей во вторую
степень, как уже было сказано выше, после
обязательно нужно сделать проверку.

10.

Приравниваем выражения, стоящие под
корнем:
Х-5=2х-3,
Х=-2
Проверка:
2 5 7
Ответ: нет решений.
При х=-2 оба
выражения, стоящие под
знаками корней будут
отрицательными, что не
соответствует определению
арифметического корня.

11.

Решите уравнение
х 6 x 1 2x 5
x 6 2 ( x 6)( x 1) x 1 2 x 5
x x 6 x 6 6 x 7 x 30 0
2
x1 3, x2 10
Сделайте проверку:
Ответ: х=3
2

12.

Решите уравнение
3
Решение:
2х 3 1
Проверка:
2( 1) 3 1
2х+3=1,
3
2х=-2,
1=1, х=-1 –
корень
уравнения.
х=-1.
Ответ: х=-1.

13.

Иногда иррациональные уравнения можно
решать так называемым графическим методом.
На стр. 62, задача№4.
ВАЖНО! Этот способ дает лишь
возможность высказать
предположение о количестве
корней, и, как правило, найти их
приближенные значения.

14.

• Решаем в классе и у доски №153(3),
№154(1,3), №155(1,3)

15.

Домашнее
задание:
§9,№152,
№153-155(чётные)