Иррациональные уравнения

1.

Иррациональными называются
уравнения, в которых переменная
содержится под знаком корня

2.

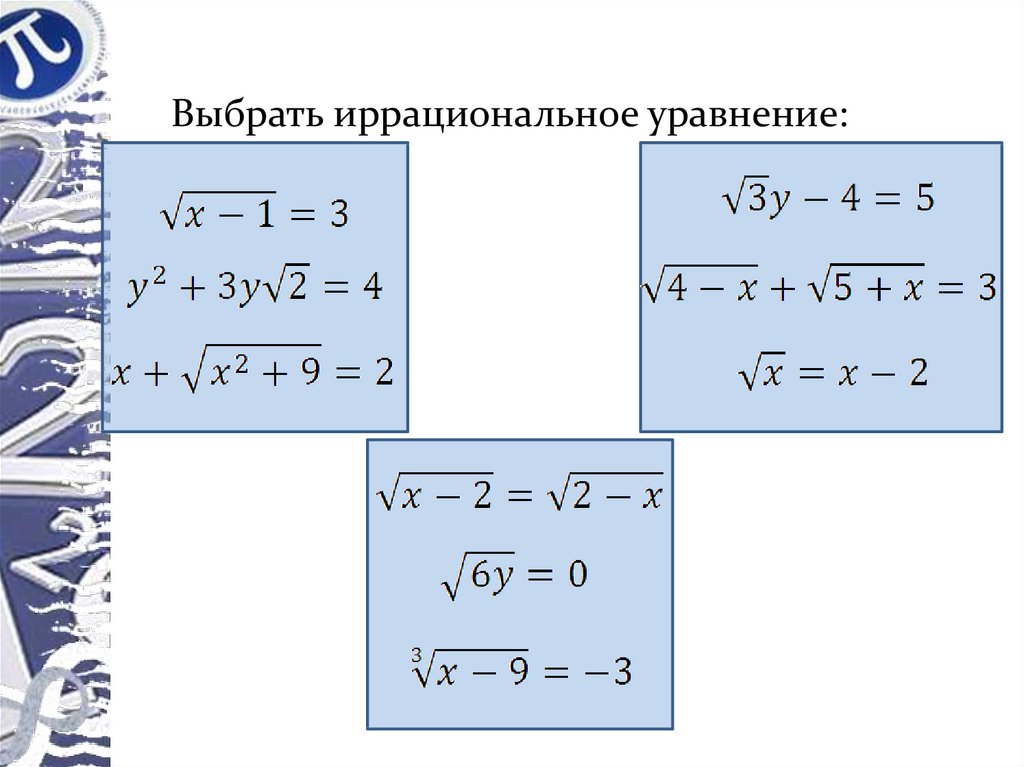
Выбрать иррациональное уравнение:

3.

Иррациональные уравнения содержат
радикалы. Чтобы избавиться от радикалов,
необходимо возвести обе части уравнения в
одну и ту же степень с натуральным
показателем.
если:
Возводим в нечетную степень, то
получаем равносильное уравнение;
Возводим в четную степень, то можем
получить посторонние корни. В этом
случае делаем проверку.

4. Алгоритм решения простейшего иррационального уравнения

1. Возвести обе части уравнения в нужную
степень.
2. Решить полученное рациональное
уравнение.
3. При необходимости проверить
полученные корни подстановкой в
исходное уравнение.
4. Выписать ответ.

5. Решить иррациональное уравнение

х х 2 2
2
( х х 2 ) (2)
2
2
х
2
2
–х-2=4
2
х –х
- 6=0
х1=3
Проверка
3 3 2 2
2
Ответ: 3; -2
х2 = 2
( 2) 2 2 2 2

6.

I
III
II
IV

7. Устная работа

• Можно ли, не решая уравнений, сделать
вывод о неразрешимости предложенных
уравнений:
7 x 8 x;
x 3 x 1
2
3 х 5 х 9
5х 7 3 4 х х 2 2 0

8. Методы решения иррациональных уравнений

• Введение новой переменной
• Исследование ОДЗ
• Умножение обеих частей уравнения на
сопряженный множитель.
• Сведение уравнения к системе
рациональных уравнений с помощью
введения переменной.
• Выделение полного квадрата

9. Методы решения иррациональных уравнений

• Использование ограниченности
выражений, входящих в уравнение
• Использование свойств монотонности
функций
• Функционально - графический метод
• Метод равносильных преобразований
• Метод возведения обеих частей уравнения
в одну и ту же степень

10. Пример. Решите уравнение:

2х х 3 0
1 способ.
х 3 2х
х
2
3 2 х
2
х 9 12 х 4 х 2
4 х 2 13 х 9 0
1
х1 2 ;
х 2 1.
4
1
Проверка : х1 2
4
9
9
2
3 0
4
4
3 0( неверно)
х2 1
2 1 1 3 0
0 0(верно)
Ответ : х 1.
2 способ.
2х х 3 0
Замена : х а
2а 2 а 3 0
3
а1 1;
а2 .
2
3
х
х 1 или
2
х 1
к.нет

11. Этот метод называется методом введения новой переменной. Примеры:

1) х х 30;
После замены
1)а 2 а 30;
20
2) а
1;
а
20
2) х
1;
х
2
3)(5 х 1) 5 х 1 12. 3)а а 12.

12. Введение новой переменной

Решение.
• Решить уравнение.
x 2 3x 18 4 x 2 3x 6 0
Пусть
x2 3x 6 t , t – неотрицательное число,
тогда имеем t 2 12 4t 0.
Отсюда, t1=2, t2=-6.
t=-6 – посторонний корень.
Выполняем обратную подстановку, получим
х2+3х-6=4
Отсюда, х1= - 5, х2=2.

13.

Исследование ОДЗ
• Решить уравнение
3 3х 1 4 3 х 7 х 1 2 1 х
Решение.
1
x 3
3 x 1 0
x 1 0 x 1
1 x 0
x 1
Замечаем, что ОДЗ
уравнения состоит
точки х=1.
Проверкой убеждаемся, что
х=1 – решение уравнения.
из одной

14. Умножение обеих частей уравнения на сопряженный множитель

x 3 x 8 5.
• Решить уравнение
Решение.
Получим,
Умножим обе части уравнения на
x 3 x 8 5
x 3 x 8
x 3 x 8 .
x 3 x 8 1,
Имеем,
x 3 x 8 5.
Отсюда,
2 х 3 4, х 1.
Проверкой убеждаемся, что х = 1 является корнем
данного уравнения.

15. Сведение уравнения к системе рациональных уравнений с помощью введения переменной

• Решить уравнение
3
х 2 х 1 3.
Решение. Положим u 3 x 2, v x 1.
Тогда u+v=3. Так как u3=x-2, v2=x+1, то v2 – u3 =3. Итак, в
новых переменных имеем
v u 3,
2 3
v u 3
Значит, х=3.
v 3 u,
3 2
u u 6u 6 0
v 2,
u 1.

16. Выделение полного квадрата

Решение.
• Решить уравнение
x 2 2 x 1 x 2 2 x 1 2.
Заметим, что
x 1
x 2 2 x 1
x 2 2
x 1 1 .
x 1 1
2
2
Следовательно,
имеем
уравнение
Данное
уравнение
равносильно
совокупности двух
2
2
систем:
xx 1 11 x x 11 1 22.,
x 1 1 0,
Ответ:
или
2 x 1 12 x 0.
x 1 1 0,
x 1 1 1 x 1 2.
Решением первой системы будет х=0, решением второй
системы – все числа, удовлетворяющие неравенству
1 х 0.

17. Использование ограниченности выражений, входящих в уравнение

• РешитьРешение.
уравнение
Так как
x2 1 1
и
x2 1 4 x4 1 2 x2 .
4
х 4 1 1 для любых значений х,
то левая часть уравнения не меньше двух для
2
Правая часть 2 х 2 для х R.
х R
Поэтому уравнение может иметь корнями только те
значения х, при которых
х 2 1 4 х 4 1 2,
2 х 2 2.
Решая второе уравнение системы, найдем х=0.
Это значение удовлетворяет и первому уравнению
системы. Итак, х=0 – корень уравнения.

18. Использование свойств монотонности функций

РешитьРешение.
уравнение
5
x 1 x 2 3 29 x.
Если функция u(x) монотонна, то уравнение и(х) = А
либо не имеет решений, либо имеет единственное
решение.
Отсюда следует, что уравнение и(х) = v(x),
где и(х) - возрастающая, a v(x) – убывающая функции,
либо не имеет решений, либо имеет единственное
решение.
Подбором находим, что х=2 и оно единственно.

19. Домашнее задание

4x2+5x
=44(x+5).
Домашнее задание
1.
x 2 14 x 47 1 x 7 1,
2. x 2
4. 3
2 х 1 х 1,
5
x 1 x 2 3,
x 2 x 20 6 x 12,
5.
3.3
5 x 3 5 x 6 25 x 2 .
7.
x x 6 x x 6 4
8.
2x 1
x 1
2
1
x 1
2x 1
9.
x x 4 x 4 0
3
10. 4 x 2
11.
3
2
6. 6
x x 7 25 4 x x 54.
x 2 x 2
x
x 2 x 2 2
12.
13.
5 x x 5 44( x 5)
2 x 1 3 x 4 17 x
14.
3
x 3 2x 3 3 12( x 1)
x 2 2 x 1 x 5 x 1 4