Similar presentations:
Свойства логарифмов
1. Свойства логарифмов
Разработала:Гусакова А.А. – преподаватель математики II квалификационной категории
ГБОУНПОПУ № 58 КК
2. Проверка домашнего задания
№ 544 (а, д, з)Найдите логарифм по основанию а, представленного
в виде степени с основанием а.
а)
3 9
2
log 3 9 2
1
д) 2
8
1
log 2 3
8
3
з)
1
2
9 3
1
log 9 3
2
3. №545 (а, в, ж)
Найдите логарифм по основанию а,представленного в виде степени с
основанием а.
а)
4
16 2
1
4
в)
49 7
1
2
16 2
49 7
1
log 16 2
4
1
log 49 7
2
ж) 81
3
4
27
3
log 81 27
4
4. Работа с карточками
Ответы на карточки:Вариант 1
Вариант 3
1. г)
2. Рис. 1
1.б)
2. Рис. 2
Вариант 2
Вариант 4
1. в)
2. Рис. 1
1.г)
2. Рис.1
5. Тема: «Свойства логарифмов».
Цель: изучить свойствалогарифмов, научиться
применять свойства
логарифмов на практике.
6. Свойства логарифмов
1.Если основание иподлогарифмическое выражения
равны, то логарифм равен единице.
log a a 1
Пример:
log 2 2 1 т.к. 2 2
1
7. 2. Логарифм по основанию «а» числа 1 равен нулю.
log a 1 0Пример:
log 3 1 0
т.к.
3 1
0
8. 3. Логарифм произведения равен сумме логарифмов.
log a x y log a x log a yПример:
log 2 4 8 log 2 4 log 2 8 2 3 5
т.к.
2 4
2
и
2 8
3
9. 4. Логарифм частного равен разности логарифмов.
xlog a log a x log a y
y
Пример:
27
log 3
log 3 27 log 3 9 3 2 1
9
т.к.
3 27
3
и
3 9
2
10. 5. Степень подлогарифмического выражения можно представить как множитель перед логарифмом.
log a x p log a xp
Пример:
log 2 4 3 log 2 4 3 2 6
3
т.к.
2 4
2
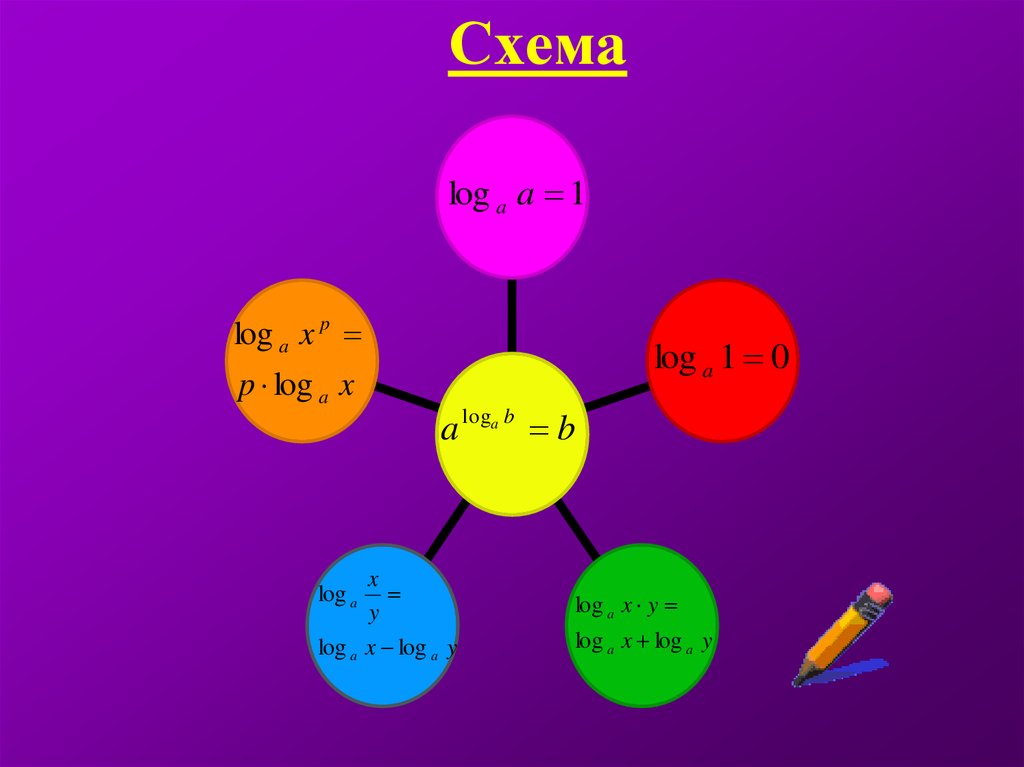
11. Схема
log a a 1log a x p
p log a x
log a 1 0
a loga b b
x
y
log a x log a y
log a
log a x y
log a x log a y
12. Самостоятельная работа. Ответы на карточки
Вариант №11. log 6 3 log 6 12
log 6 3 12
log 6 36 2
2. log 7 x log 7 12 log 7 4
12
log 7 x log 7
4
log 7 x log 7 3
х 3
Вариант №2
1.
log 3 45 log 3 5
45
5
log 3 9 2
log 3
2. log x log 15 log 5
4
4
4
15
5
log 4 x log 4 3
log 4 x log 4
х 3
13. Запишите ваше домашнее задание!!!
Повторить конспект,Прочесть учебник на странице 193-197,
Выполнить номера 562 (б, в), 563 (б, в).












 mathematics
mathematics








