Определение квадратного уравнения. Неполные квадратные уравнения

1.

«Определение квадратного уравнения. Неполные
квадратные уравнения»

2. ax+b=0

Задание:
ax+b=0
1) (2х-3)2-2х(4+2х)=49,
2) y2+80=81,
3) -z+4=47,
4) 2x2+3х+1=0,
5) 4k/3+4=k/2+1,
6) 12s-4s2=0,
7) 10+p2-4p=2(5-3p),
8) 6(t-1)=9,4-1,7t,
9) 3y+y2-8=y2+y+6,
10) 5х2-6х+1=0.
1) -20х-40=0
3) -z-43=0
5) 5k+18=0
8) 7,7t-15,4=0
9) 2y-14=0
Ответы:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
x= - 2
y= - 1; 1
z= - 43
?
k= - 3,6
s=0; 3
p=0; - 2
t=2
y=7
?

3.

Цели
урока:
1. Выучить определение квадратного
уравнения.
2. Научиться определять по виду уравнения
является ли оно квадратным или нет.
3. Научиться определять вид квадратного
уравнения - полное оно или неполное.
4. Научиться выбирать нужный алгоритм
решения неполного квадратного уравнения.

4.

a b c
2xx2 + 3хх -+9 = 0,
a b c
5х
х2 2+- 6х
х+1=0
2
1. Есть x .
2. Есть х.
3. Есть число.
4. Есть нуль в правой части.

5.

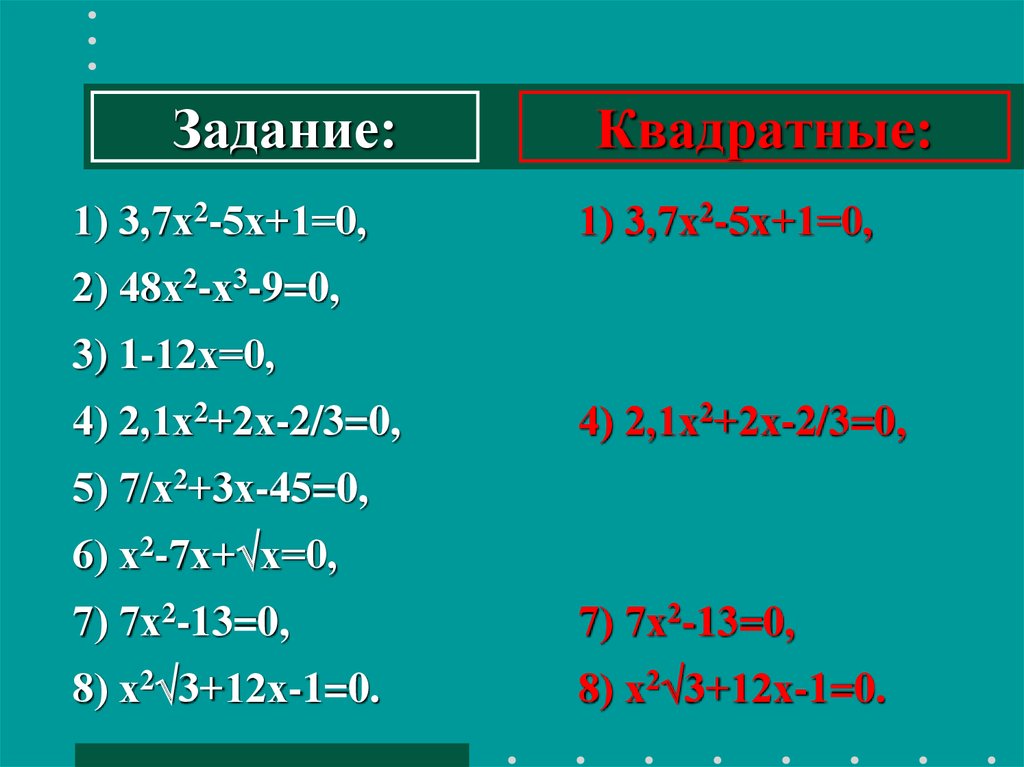
Задание:
1) 3,7х2-5х+1=0,
Квадратные:
1) 3,7х2-5х+1=0,
2) 48х2-х3-9=0,
3) 1-12х=0,
4) 2,1х2+2х-2/3=0,
4) 2,1х2+2х-2/3=0,
5) 7/х2+3х-45=0,
6) х2-7х+ х=0,
7) 7х2-13=0,
7) 7х2-13=0,
8) х2 3+12х-1=0.
8) х2 3+12х-1=0.

6.

Задание:
1) 3,7х
1)
3,7х2-5х+1=0,
2) -х2=0
3) 2,1х
3)
2,1х2-2/3+2х=0,
4) 7х
4)
7х2-13=0
5) х2 3+12х-1=0,
6) -10+3х+х2=0.
7) х2/7-3х=0.
Ответы:
1)
2)
3)
4)
a=3,7
a= -1
a=2,1
a=7
b= -5
b=0
b=2
b=0
c=1
c=0
c= -2/3
c= -13
5) a= 3 b=12 c= -1
6) a=1 b=3 c= -10
7) a=1/7 b= -3 c=0

7.

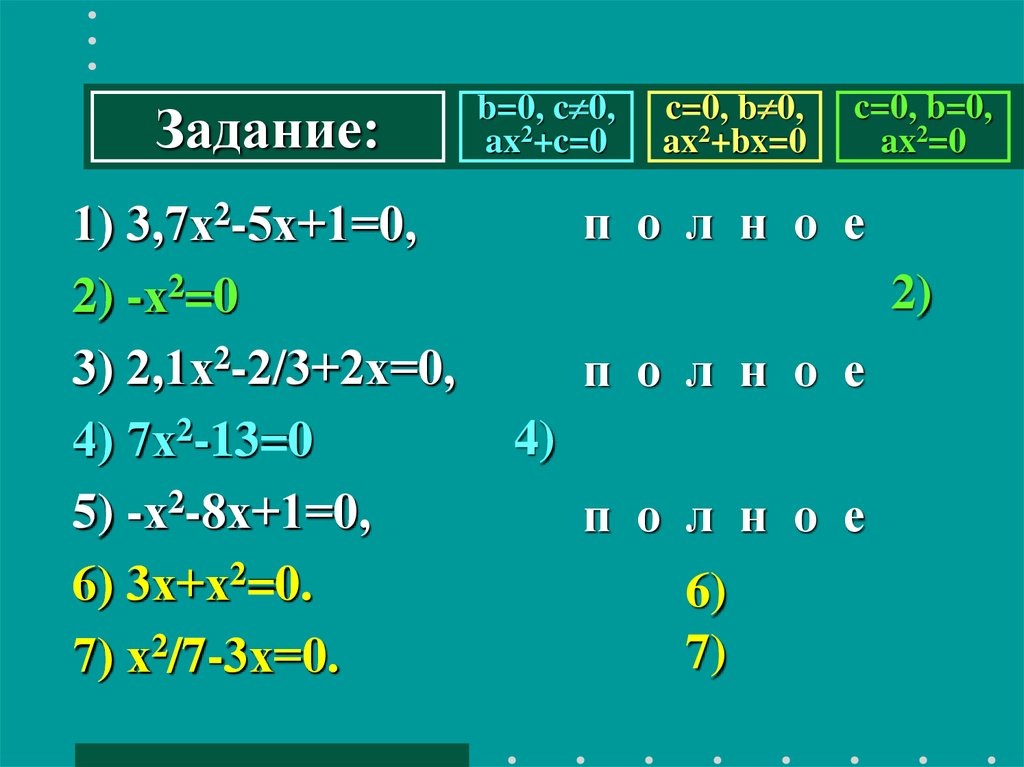
Задание:
1) 3,7х2-5х+1=0,
1)
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) -х2-8х+1=0,
6) 3х+х2=0.
7) х2/7-3х=0.
b=0, c 0,
ax2+c=0
c=0, b 0,
ax2+bx=0
c=0, b=0,
ax2=0
п о л н о е
2)
п о л н о е
4)
п о л н о е
6)
7)

8. 4x2-9=0

b=0, c 0, ax2+c=0
1) перенести
свободный член в
правую часть,
2) разделить обе
части уравнения на
а 0,
3) если -с/а>0, то два
корня:
х1= -с/а и х2= - -с/а;
если -с/а<0, то корней
нет.
4) записывается ответ
4x2-9=0
6v2+24=0
1) 4x2=9,
1) 6v2=-24,
2) x2=9:4,
2) v2=-24:6,
x2=2,25,
v2=-4,
3) корней
3) х1= 2,25,
нет, т.к. х2= - 2,25,
4<0
х1=1,5,
х2=-1,5,
4) Ответ: х1=1,5, 4) Ответ:
корней нет
х2=-1,5,

9. 3x2-4x=0

c=0, b 0, ax2+bx=0
3x2-4x=0
-5х2+6х=0
1) х(3х-4)=0,
1) х(-5х+6)=0,
1) разложить левую
часть на множители,
2) x=0 или
2) каждый множитель 2) x=0 или
приравнивается к
3х-4=0
-5х+6=0
нулю,
3) решается каждое
3) х=0 или
3) х=0 или
уравнение,
3х=4,
-5х=-6,
х=4:3,
х= -6:(-5),
х=11/3,
х=1,2
4) записывается ответ 4) Ответ: х1=0, 4) Ответ: х1=0,
х2=11/3.
х2=1,2.

10. -x2=0

c=0, b=0, ax2=0
-x2=0
9х2=0
1) разделим обе
части на а 0,
х2=0,
2) х=0,
1) x2=0,
1) x2=0,
2) x=0
2) x=0
3) записывается
ответ.
3) Ответ:
х=0.
3) Ответ:
х=0.

11.

Задание:
Алгоритмы:
1) 7х2-13=0,
первый
2) 7k-14k2=0,
второй
3) 12g2=0,
третий
4) 5y2-4y=0,
второй
5) 2h+h2=0,
второй
6) 35-х2=0,
первый

12.

Домашнее задание:
Легче:
Сложнее:
п.19,
п.19,
№ 505,
№ 505,
№ 509(б, в, г, е),
№ 509(г, е),
№ 511.
№ 511(а, г, д),
№ 513(а, б).