Similar presentations:
Тригонометрические формулы. 10 класс
1. Тригонометрические формулы
2. Цель урока
• Повторение изученного материала• Подготовка к контрольной работе
3. Задачи урока
• Повторить определение синуса, косинуса, тангенса,котангенса числа α;
• Повторить формулы приведения, формулы двойного угла,
формулы сложения;
• Повторить основное тригонометрическое тождество и
формулы, выражающие связь между тангенсом и
косинусом, между котангенсом и синусом.
• Научить применять полученные знания при решении
задач.
4. Ход урока
1.2.
3.
4.
5.
6.
7.
Блиц-опрос
Закрепление знаний и умений
Самостоятельная работа (тест)
Проверка самостоятельной работы
Это интересно
Итог урока
Домашнее задание
5.
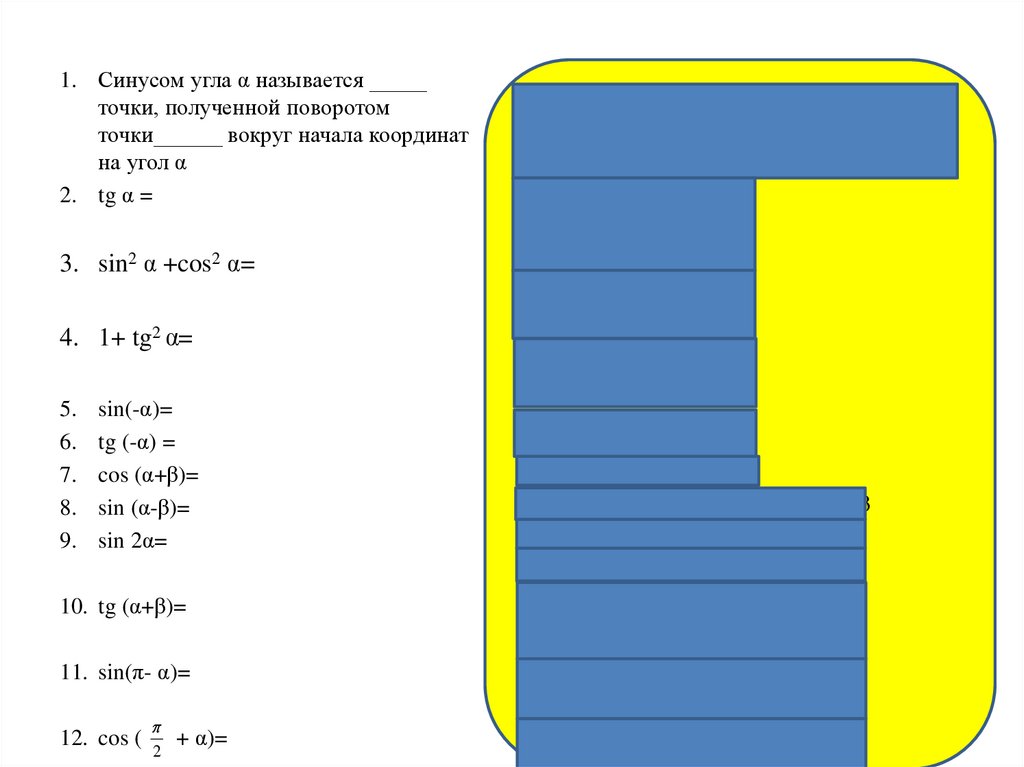
1. Синусом угла α называется _____точки, полученной поворотом
точки______ вокруг начала координат
на угол α
2. tg α =
1. Синусом угла α называется ордината
точки, полученной поворотом точки
(1;0) вокруг начала координат на угол α
2. tg α =
3. sin2 α +cos2 α=
sin
cos
3. sin2 α +cos2 α = 1
4. 1+ tg2 α=
4. 1+ tg2 α =
5.
6.
7.
8.
9.
sin(-α)=
tg (-α) =
cos (α+β)=
sin (α-β)=
sin 2α=
5.
6.
7.
8.
9.
1
cos 2 α
sin(-α) = - sin α
tg (-α) = -tg α
cos (α+β) = cosα cosβ – sinα sinβ
sin (α-β) = sinα cosβ - cosα sinβ
sin 2α = 2sin αcos α
10. tg (α+β)=
10. tg (α+β) =
tg tg
1 - tg tg
11. sin(π- α)=
12. cos (
2
+ α)=
11. sin(π- α) =sin α
12. cos ( + α) = -sinα
2
6.
1. Косинусом угла α называется _____точки, полученной поворотом
точки______ вокруг начала координат
на угол α
2. ctg α=
3. tg α∙ ctg α=
4. 1+ ctg2 α=
5.
6.
7.
8.
9.
cos (-α)=
ctg (-α) =
cos (α-β)=
sin (α+β)=
cos 2α=
11. cos(π- α)=
12. sin (
2
cos
2. сtg α= sin
3. tg α∙ ctg α = 1
4. 1+ ctg2 α=
5.
6.
7.
8.
9.
1
sin 2 α
cos (-α) = cos α
ctg (-α) = -ctg α
cos (α-β)=cosα cosβ +sinα sinβ
sin (α+β)= sinα cosβ + cosα sinβ
cos 2α=cos2 α-sin2 α
2tg
1 - tg 2
10. tg 2α=
1. Косинусом угла α называется абсцисса
точки, полученной поворотом точки
(1;0) вокруг начала координат на угол α
+ α)=
10. tg 2α=
11. cos(π- α)= - cos α
12. sin (
2
+ α)=-cos α
7. Закрепление знаний и умений
1) Дано:sin
3
;
3 2
Найти: cos
ОТВЕТ:
2
cos
3
8.
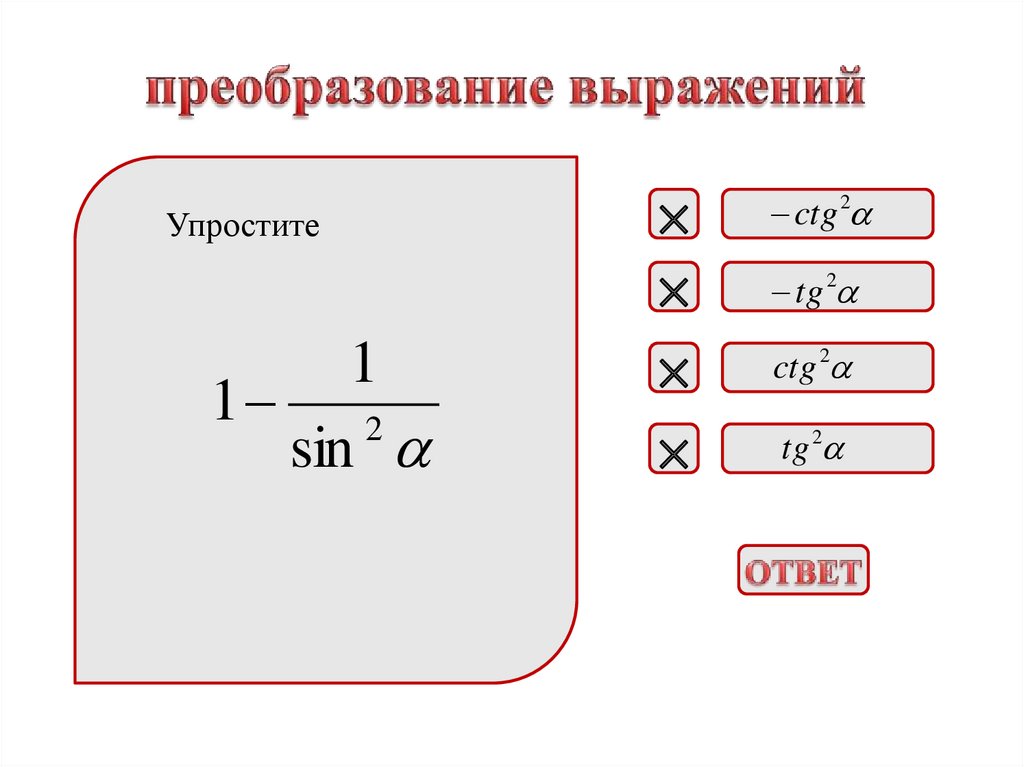
Упростите1 cos
2
cos
2
1 / sin 2
1 / cos 2
ctg 2
tg 2
9.
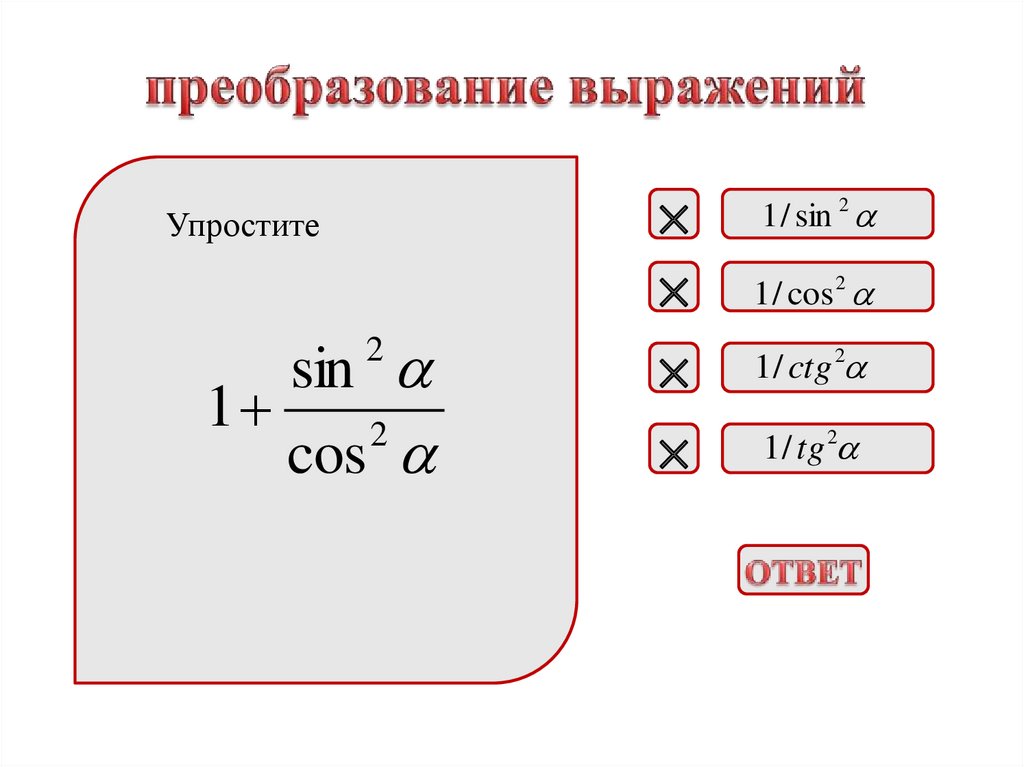
Упроститеsin
1
2
cos
2
1 / sin 2
1 / cos 2
1 / ctg 2
1 / tg 2
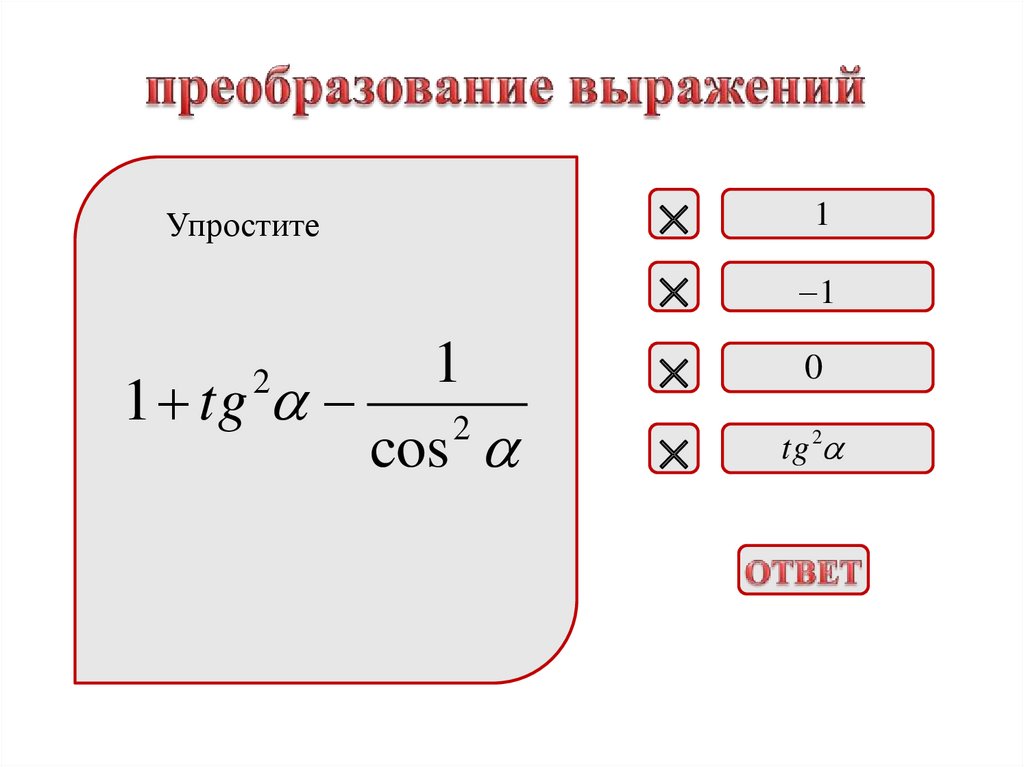
10.
Упростите1
1 tg
2
cos
2
1
1
0
tg 2
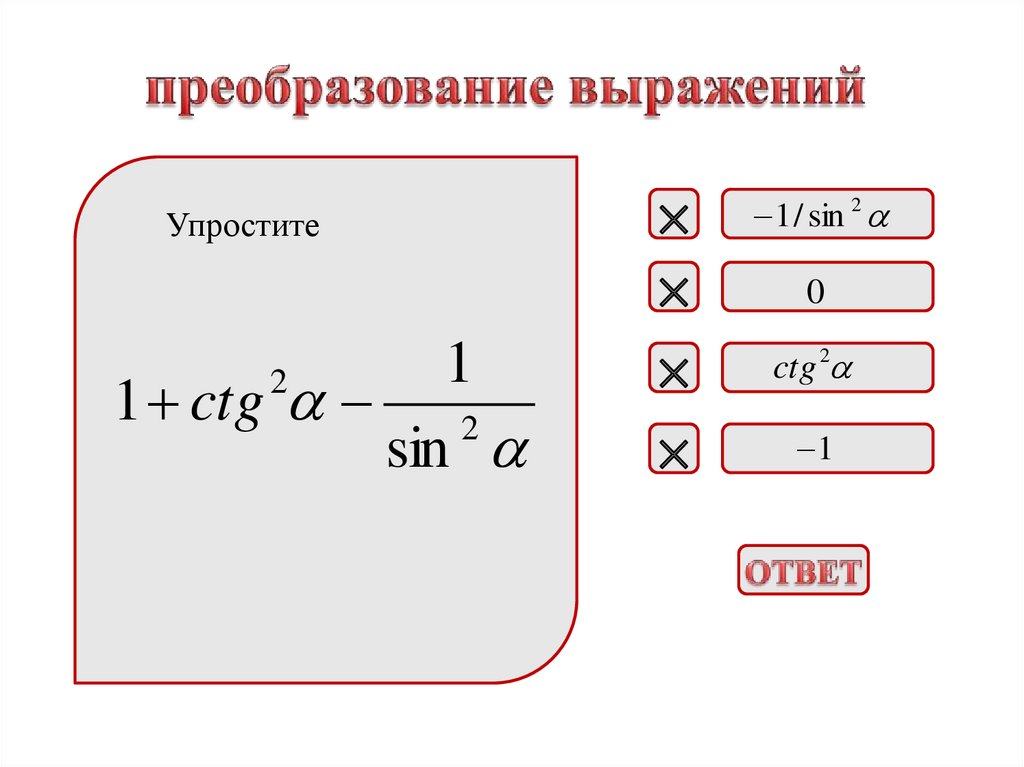
11.
Упростите1
1 ctg 2
sin
2
1 / sin 2
0
ctg 2
1
12.
Упростите1
1 2
sin
ctg 2
tg 2
ctg 2
tg 2
13.
2) Вычислить:Дано:
Найти:
ОТВЕТ:
tg 2 2 ;0
sin
2 2
sin
3
2
14.
Упростить выражение3) 2 sin( ) cos 2 cos( ) sin( )
2
2
Ответ: -2
4)
(1 tg( )) (1 tg( )) cos
Ответ:
2
cos 2
15.
5) Доказать:2
6) Доказать:
2
2 sin 2 sin 4
tg
2 sin 2 sin 4
16.
вариан 11)
а) -2,5;
2)
вариант 2
Найдите значение
1) Найдите значение
2
3 sin 120 4 cos180 3tg135
2 cos 2 150 3 sin( 90 ) 5ctg135
б) 5,5;
Дано:
в) -4,75;
3
sin ;
5 2
Найдите значение:
а)
3)
31
20
б)
г) 3,25.
1
20
в)
а) -3,5;
2)
cos tg
1
20
г)
sin 2 в) cos г) sin
3)
г) 6,5.
4 3
cos ;
2
5 2
Дано:
а)
Упростите выражение:
а) cos б)
в) -0,5;
Найдите значение:
31
20
1 (1 sin ) (1 sin )
tg cos
б) 9,5;
11
15
б)
1
sin ctg
11
г)
15
14
в)
15
1
14
15
Упростите выражение:
ctg sin
1 (sin cos ) 2
а) 2 cos
б)
1
2 cos
в)
2 sin
г)
1
2 sin
17. Проверка
1 вариант1. г)
2. б)
3. г)
2 вариант
1. б)
2. в)
3. г)
18. Это интересно
19. Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее
«измерение треугольников».Одним из основоположников
тригонометрии считается
древнегреческий астроном Гиппарх,
живший во 2 веке до нашей эры.
Гиппарх является автором первых
тригонометрических таблиц и
одним
из
основоположников
астрономии.
20.
Тригонометрия и ее применение вразличных сферах науки и жизни
,
k=1, a=1
В архитектуре
Детская школа Гауди в Барселоне
21.
Сантьяго КалатраваВинодельня «Бодегас Исиос»
22.
Феликс КанделаРесторан в Лос-Манантиалесе
23. Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону),
Тригонометрия в физикеКолебания, при которых изменения физических
величин происходят по закону косинуса или синуса
(гармоническому закону), называются
гармоническими колебаниями.
Выражение, стоящее под знаком косинуса или синуса,
называется фазой колебания:
24. Теория радуги
n1sin α
=
sin β
n2
n1 - показатель преломления первой среды
n2 - показатель преломления второй среды
α-угол падения, β-угол преломления света
Северное сияние
F q B q B sin
25. Тригонометрия в биологии
26.
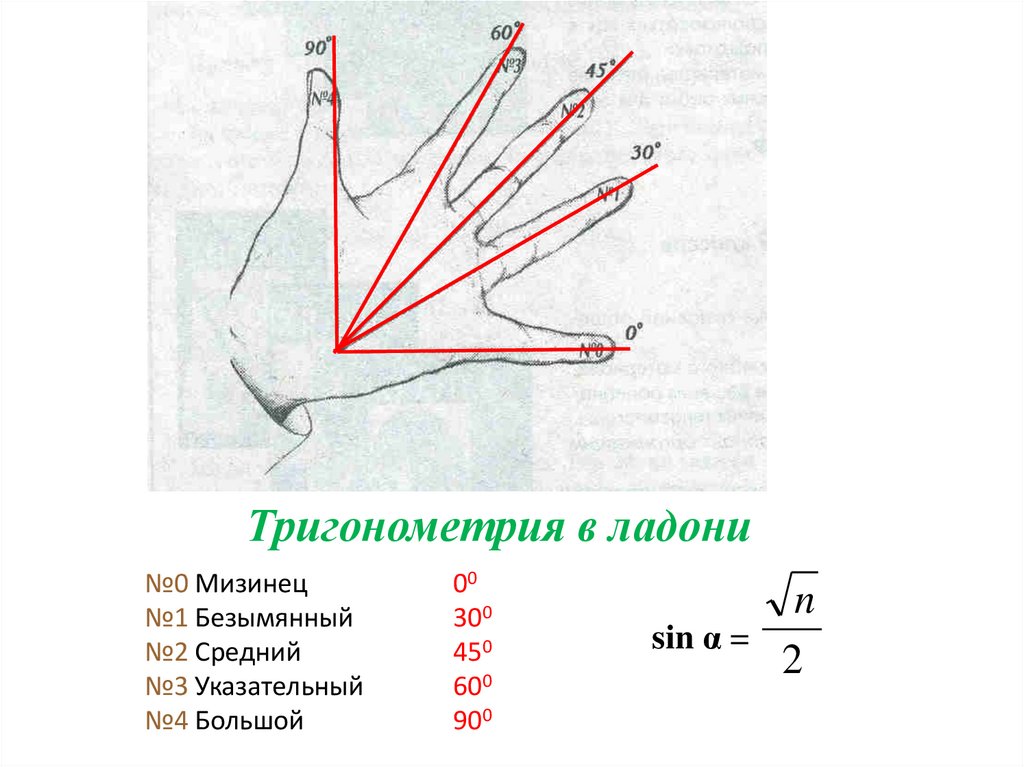
Тригонометрия в ладони№0 Мизинец
№1 Безымянный
№2 Средний
№3 Указательный
№4 Большой
00
300
450
600
900
n
sin α =
2
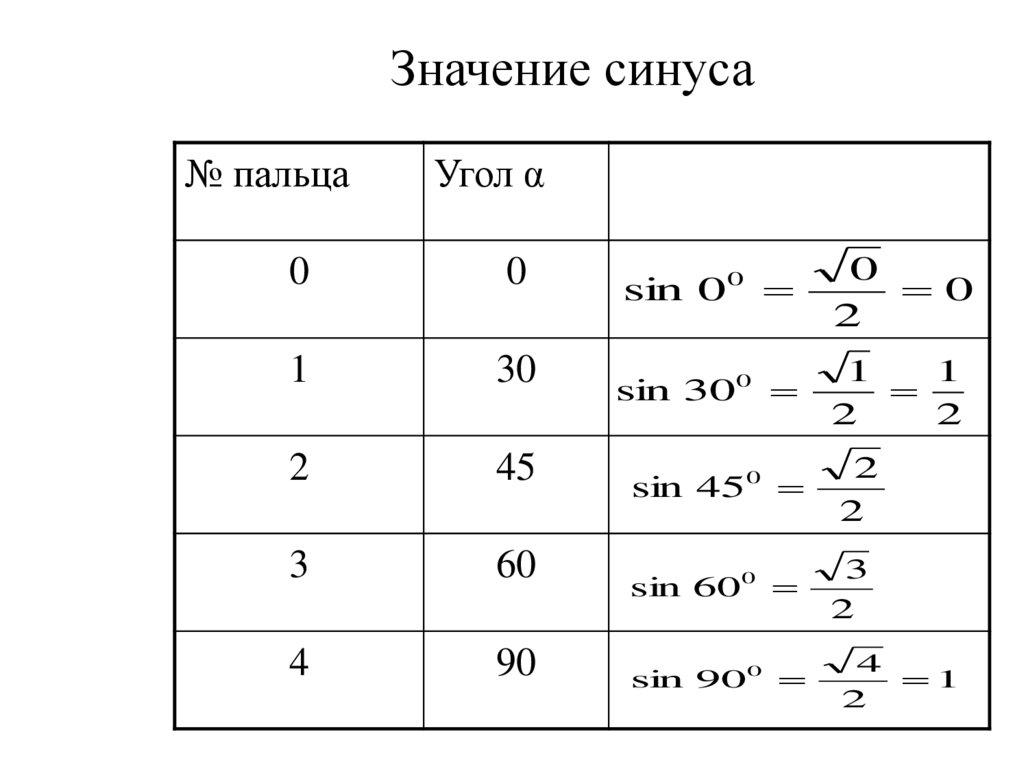
27.
Значение синуса№ пальца
Угол α
0
0
sin 0 0
0
0
2
1
30
sin 30 0
1
1
2
2
2
45
sin 450
3
60
4
90
sin 60 0
sin 90 0
2
2
3
2
4
1
2
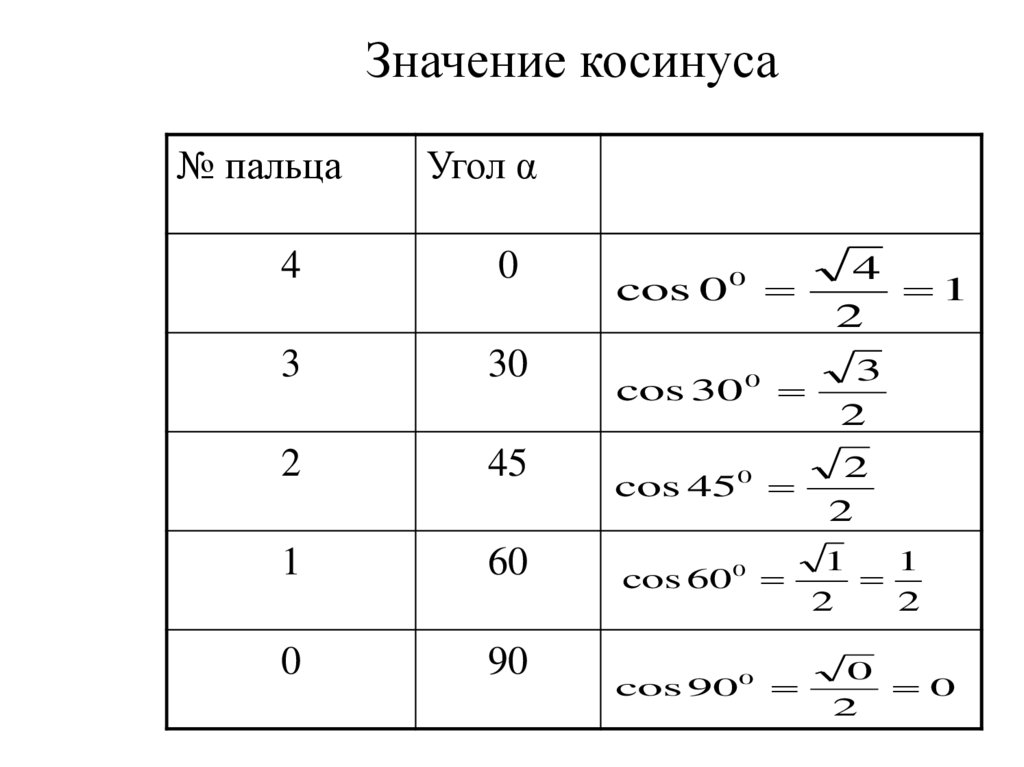
28.
Значение косинуса№ пальца
Угол α
4
0
3
30
2
45
1
60
0
90
cos 0 0
4
1
2
cos 30 0
3
2
cos 45
0
cos 60 0
cos 90 0
2
2
1
1
2
2
0
0
2
29.
БиоритмыЭкологические ритмы : суточные, сезонные (годовые), приливные и лунные циклы
Физиологические ритмы: ритмы давления, биения сердца, артериальное давление.
30. Домашнее задание
стр. 12 № 14,15а),б)Стр.20 № 31
o Стр.21 № 38,39 а),б)
Доказать:
2
2 sin 2 sin 4
tg
2 sin 2 sin 4
31.
МАТЕРИАЛ К УРОКУ ПОДОБРАНИЗ РАЗЛИЧНЫХ САЙТОВ
ИНТЕРНЕТА























 mathematics
mathematics








