Similar presentations:
Решение неполных квадратных уравнений
1. Тема нашего урока: Решение неполных квадратных уравнений
Цели: Сформировать умения решатьнеполные квадратные уравнения различных
видов.
Развивать грамотную математическую речь,
умения анализировать свою деятельность.
развивать внимание, сообразительность,
быстроту реакции, логики, мышления;
воспитывать чувства ответственности.
2. Повторим:
Какое уравнение называетсяквадратным?
Как называются коэффициенты
квадратного уравнения?
Может ли коэффициент а равняться
нулю?
Какое квадратное уравнение
называется неполным?
Как преобразовать неприведенное
квадратное уравнение в приведенное?
3. Установите соответствие между видом уравнения в левой колонке с его названием в правой колонке.
Установите соответствие междувидом уравнения в левой
колонке с его названием в
правой колонке.
ах²+вх+с=0
ах²+с=0
х²+вх+с=0
неполное
приведенное
квадратное
4. Выберите уравнения, являющееся квадратным.
а) х² - 4 = ( х – 2)²;б) х² - х = 0;
в) 17х + 4 = 0;
г) 0х² + 15х + 2 = 0;
д) – 8х³ + 2 = 0.
5. Какое из уравнений имеет корни?
А) (х + 2)² = -1;Б) х² - 2х + 2 = 0;
В) х² + 1 = 0;
Г) х² - 3х = 0;
Д) (х – 3)² + 4 = 0.
6. Выберите верное утверждение.
А) уравнение вида ах² + вх + с = 0, гдеа,в,с – заданные числа и в≠0, хнеизвестное, называется квадратным;
Б) уравнение х² = а имеет корни при а‹0;
В) х = 3 является корнем уравнения
(х² - 9):(х – 3) = 0;
Г) х² - 2х + 3 = (х – 2) ² - 1;
Д) квадратное уравнение ах² + вх + с = 0
называется неполным, если один из
коэффициентов в или с равен 0.
7. Решите уравнения:
Х² =16Х² = -100
А² = 5
У² = 0
В² = 1/49 С² +1 = 50
2М²= 98 2Х² = - 8
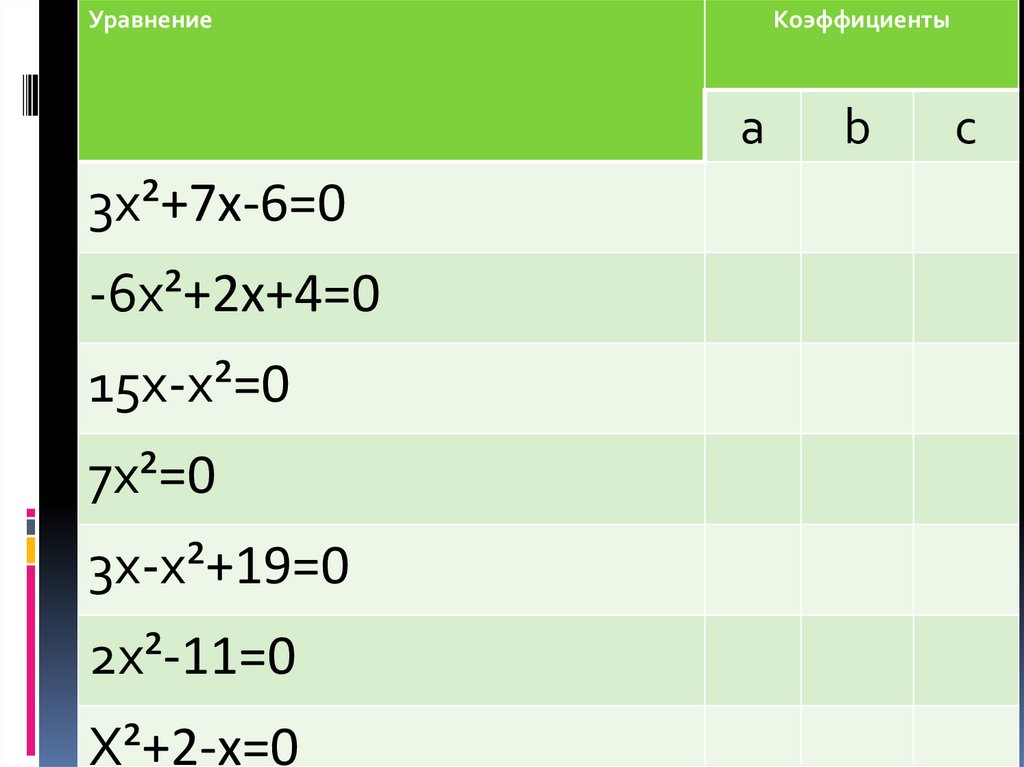
8.
УравнениеКоэффициенты
а
3х²+7х-6=0
-6х²+2х+4=0
15х-х²=0
7х²=0
3х-х²+19=0
2х²-11=0
Х²+2-х=0
b
с
9. Немного из истории решения квадратных уравнений.
Найденные древние вавилонские глиняные таблички,датированные где-то между 1800 и 1600 годами до н.э.,
являются самыми ранними свидетельствами об изучении
квадратных уравнений. На этих же табличках изложены
методы решения некоторых типов квадратных уравнений.
Древнеиндийский математик Баудхаяма в VIII столетии до
н.э. впервые использовал квадратные уравнения в форме
ax2 = c и ax2 + bx = c и привел методы их решения.
Вавилонские математики примерно с IV века до н.э. и
китайские математики примерно со II века до н.э.
использовали метод дополнения квадрата для решения
уравнений с положительными корнями. Около 300 года до
н.э. Эвклид придумал более общий геометрический метод
решения.
Первым математиком, который нашел решения уравнения
с отрицательными корнями в виде алгебраической
формулы, был Брахмагупта (Индия, VII столетие нашей
10. Пример №1: 3,8х²=0
Разделим обе части уравнения на 3,8.Что получим?
Решим уравнение Х²=0
Вывод:
Уравнение вида ах²=0 имеет
единственный корень
равный 0
11. -3Х²+21=0
Решение:1.Перенесем свободный член в
правую часть.
2.Разделим обе части
уравнения на -3
3.Решим уравнение х² = 7
12. Решите самостоятельно:
4х²+6=013.
Решение: 4х²+6=04х²=-6
х²=-6:4
х²= - 1,5
х= корней нет
14. Вывод:
Уравнения видаах²+с=0 может иметь
либо два корня , либо
ни одного.
15. Решите вместе:
5х²+7х=016.
Решение: 5х²+7х=0х(5х+7)=0
х=0 5х+7=0
5х=-7
х=-7:5
х=-1,4
17. Вывод:
Уравнения видаах²+вх=0 имеет два
корня: х=0
постоянный корень и
х = -в/а
18. Формирование ЗУН:
№515 (д,е)№517 (1 строку)
№518( любые два на
выбор) –
самостоятельно.
№521 любое на выбор
19. Итог урока:
Какое квадратное уравнениеназывается неполным?
Какие существуют виды
неполных квадратных
уравнений?
Как решается уравнение в
котором коэффициенты в=0,
с=0? Сколько корней имеет
такое уравнение?
20. Заключение.
Математика, как и любая другая наука нестоит на месте, вместе с развитием общества
меняются и взгляды людей, возникают новые
мысли и идеи. И XX век не стал в этом смысле
исключением. Появление компьютеров
внесло свои корректировки в способы
решения уравнений и значительно их
облегчило. Но компьютер не всегда может
быть под рукой (экзамен, контрольная),
поэтому знание хотя бы самых главных
способов решения уравнений необходимо
знать. Использование уравнений в
повседневной жизни – редкость. Они нашли
свое применение во многих отраслях
хозяйства и практически во всех новейших
технологиях.
21. Домашнее задание:
Примеры в параграфе№21
№517 (2 строка)
519-устно
№523 по желанию и
возможности.
22. Рефлексия:
Понял, знаюхорошо
Не понял, не
знаю














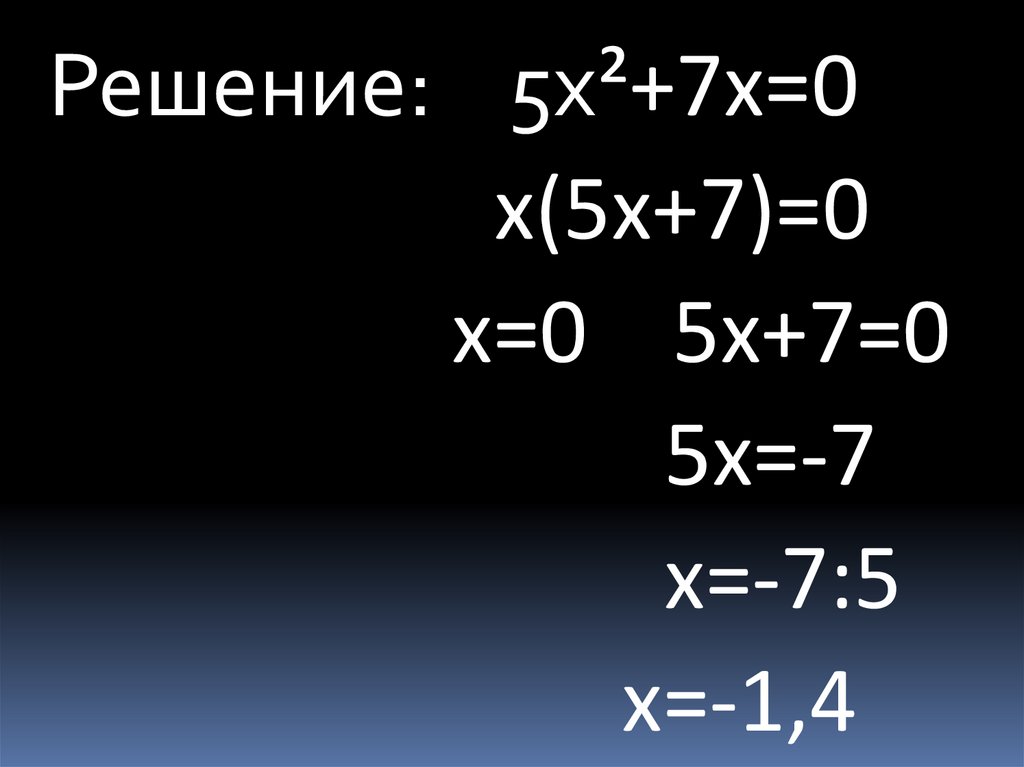






 mathematics
mathematics








