Тригонометрические функции

1.

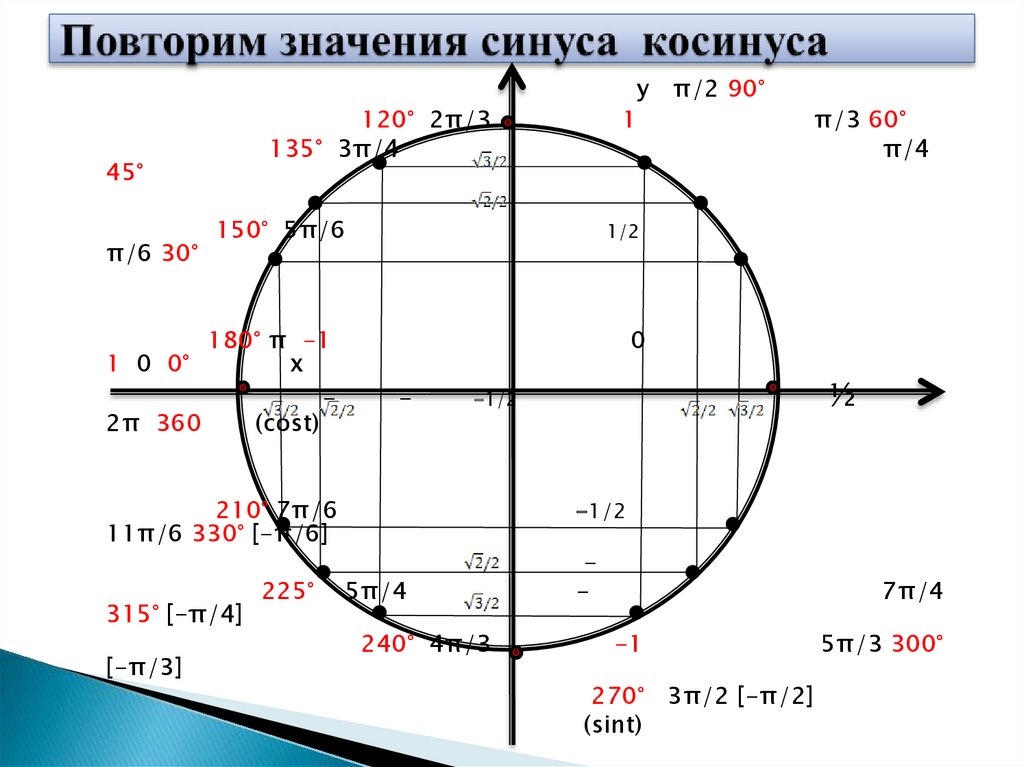
2. Повторим значения синуса косинуса

120° 2π/3
135° 3π/4
45°
π/6 30°
150° 5π/6
180° π -1
1 0 0°
x
2π 360
(cost)
315° [-π/4]
225°
π/3 60°
π/4
1/2
0
-
½
-1/2
210° 7π/6
11π/6 330° [-π/6]
[-π/3]
у π/2 90°
1
-1/2
5π/4
240° 4π/3
-
7π/4
-1
270° 3π/2 [-π/2]
(sint)
5π/3 300°

3. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

4. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

5.

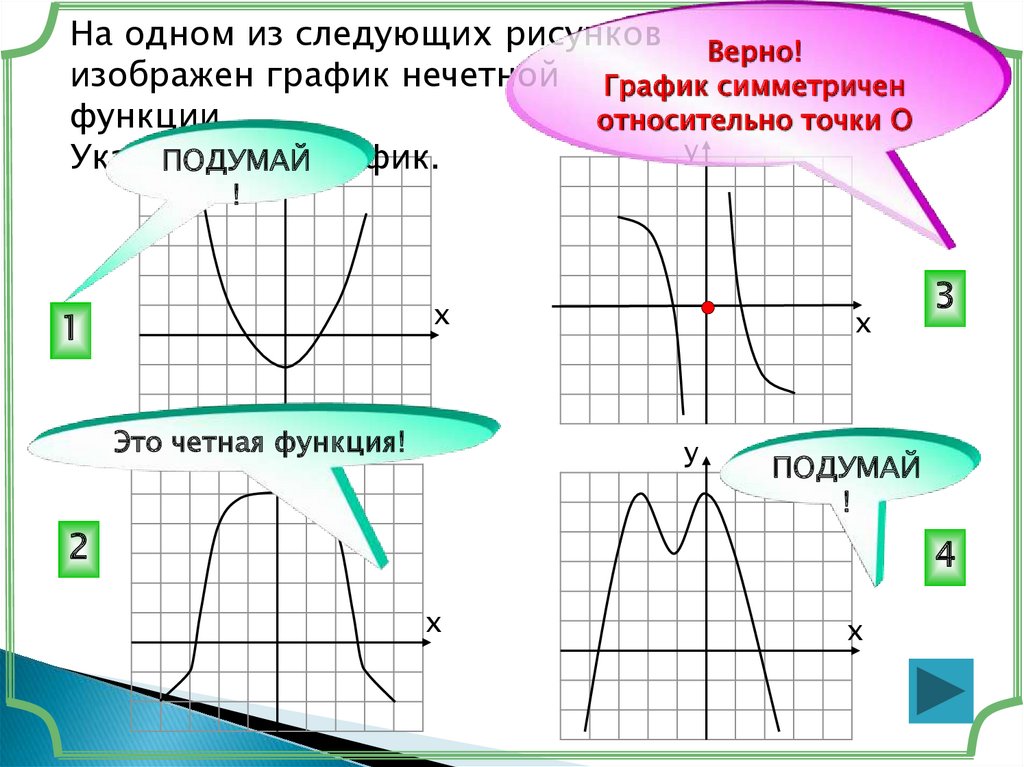
На одном из следующих рисунков Верно!
изображен график нечетной График симметричен
функции.
относительно точки О
у
Укажите
этот уграфик.
ПОДУМАЙ
!
х
1
Это четная функция!
у
х
у
3
ПОДУМАЙ
!
2
4
х
х

6.

Математический диктант
Функция задана графиком.
Укажите область определения
этой функции.
ПОДУМАЙ
!
1
[-2; 4]
2
[-5; 5)
3
[-5; 5]
4
(-2; 4]
ВЕРНО!
7
6
5
4
3
2
1
ПОДУМАЙ
-7 -6 -5 -4 -3 -2 -1
-1 1 2 3 4 5 6 7
!
Это множество
значений!
-2
-3
-4
-5
-6
-7

7.

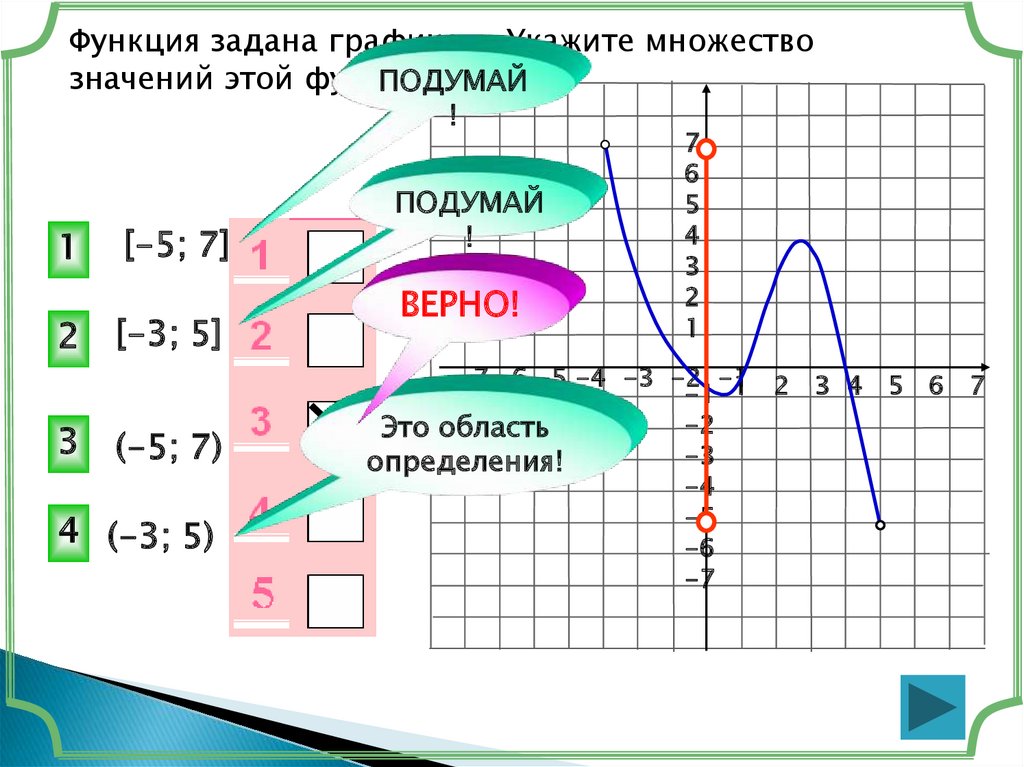
Функция задана графиком. Укажите множество
значений этой функции.
ПОДУМАЙ
!
1
2
3
[-5; 7]
[-3; 5]
(-5; 7)
4 (-3; 5)
ПОДУМАЙ
!
ВЕРНО!
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1 1 2 3 4 5 6 7
-2
Это область
-3
определения!
-4
-5
-6
-7

8.

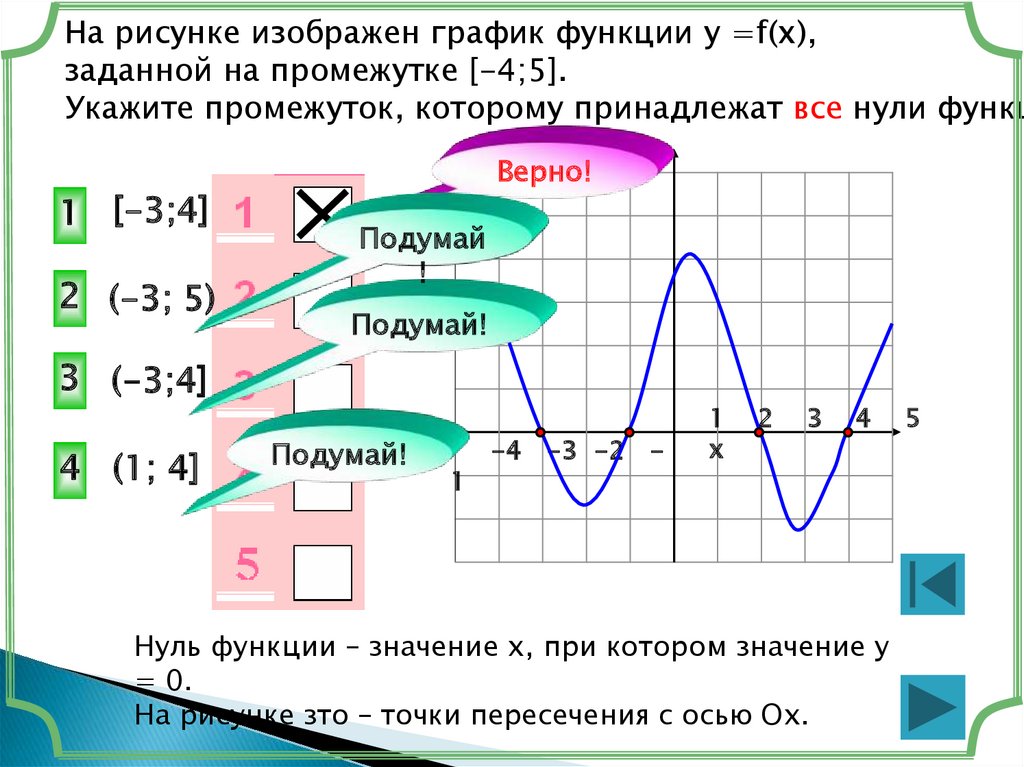
На рисунке изображен график функции у =f(x),
заданной на промежутке [-4;5].
Укажите промежуток, которому принадлежат все нули функц
1 [-3;4]
2 (-3; 5)
Верно!
Подумай
!
Подумай!
3 (-3;4]
4 (1; 4]
Подумай!
1
-4 -3 -2 -
1
х
2
3
4
Нуль функции – значение х, при котором значение у
= 0.
На рисунке зто – точки пересечения с осью Ох.
5

9.

Функция у =f (x), имеющая период Т = 4 задана
графиком на промежутке [-1; 3].
Найдите значение этой функции при х = 10.
1 способ
y
4
3
2
1
–5
15
–1 –1 1 2 2 23 3
Не верно!
1
4
Не верно!
2 1
x
7 10
Не верно!
3 3
x
11
Верно!
4 2
2 способ
f(x+Т) = f(x) = f(x-T)
Проверка (2)
f(10) = f(6) = f(2) =
…

10.

y = sin(x )
y
2
2
т
3
2
1
-1
2
x
3
2
2
1

11.

y
y = cos x + 2
2
2
т
3
2
1
-1
2
x
3
2
2
2

12.

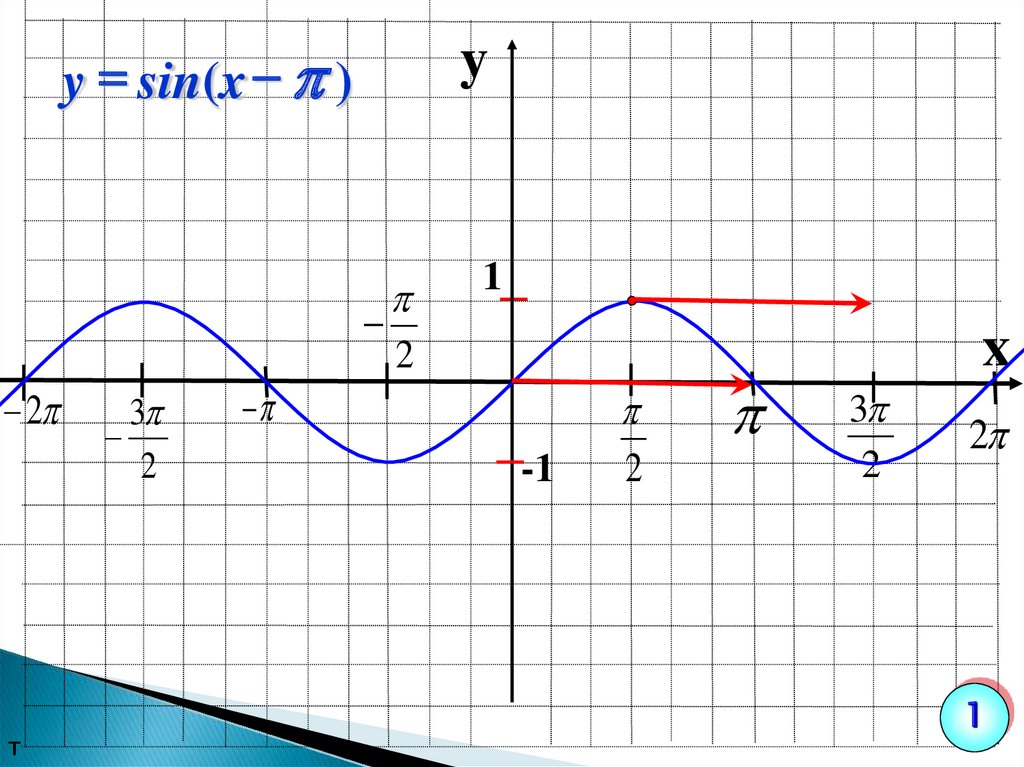
y
y = sin(x )
3
2
2
т
3
2
1
-1
2
x
3
2
2
3

13.

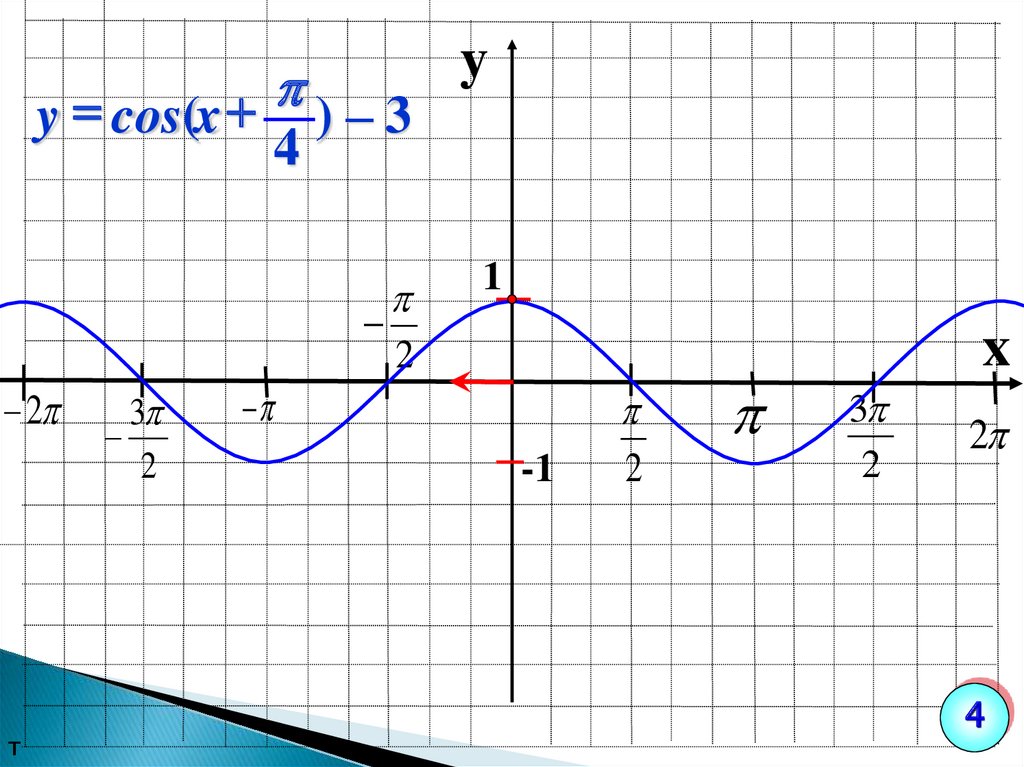
y = cos(x ) – 3
y
4
2
2
т
3
2
1
-1
2
x
3
2
2
4

14.

I
y
I
3
2
I
2
OI
Найти область значений функции
1
-1
2
I
3
2
2
I
7
2
5
2
3
I
x
3
y = sin(x ) + 2
2
E( y ) : y [1;3]
5

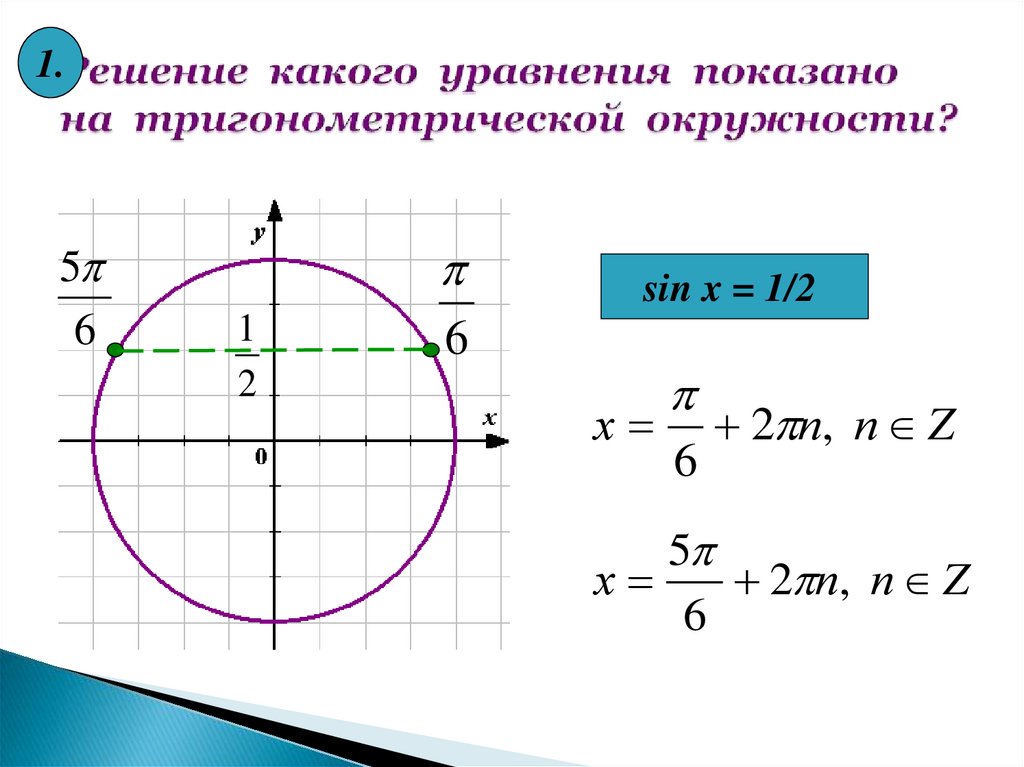
15. Решение какого уравнения показано на тригонометрической окружности?

1.
5
6
1
2
6
sin x = 1/2
х=
6
2 п, п Z
5
х=
2 п, п Z
6

16. Решение какого уравнения показано на тригонометрической окружности?

2.
4
cos x = √2/2
х=
2
2
4
х=
4
4
2 п, п Z
2 п, п Z

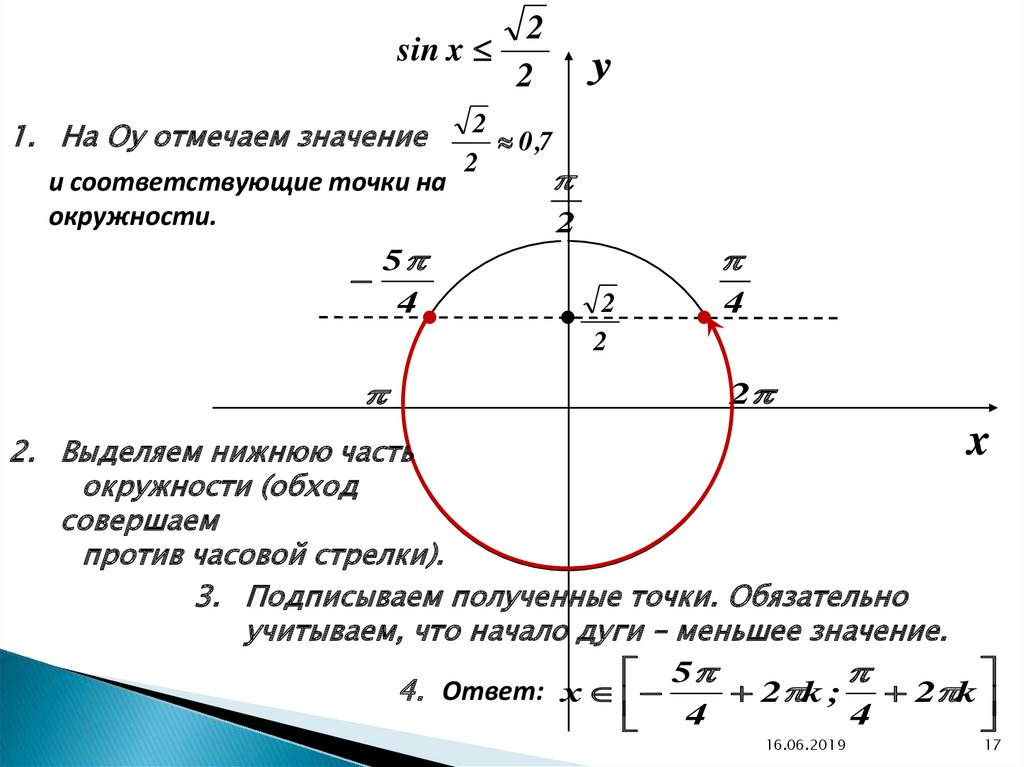
17.

sin x
1. На Оу отмечаем значение
и соответствующие точки на
окружности.
5
4
2
2
y
2
0 ,7
2
2
2
2
4
2
x
2. Выделяем нижнюю часть
окружности (обход
совершаем
против часовой стрелки).
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
4. Ответ: х
2 k ; 2 k
4
4
16.06.2019
17

18.

sin x
3
2
y
1. На Оу отмечаем значение 3 0 ,8
2
и соответствующие точки на
окружности.
2
2. Выделяем верхнюю часть
окружности (обход
совершаем
против часовой стрелки).
2
x
3
2
4
3
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4
4. Ответ: х
2 k ;
2 k
3
3
16.06.2019
18

19.

1
cos x
2
y
1. На Оx отмечаем значение 1
и соответствующие точки на
окружности.
2
2
3
1
2
2
x
2. Выделяем левую часть
окружности (обход
совершаем
5
против часовой стрелки).
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
4. Ответ: х 2 k ;
2 k
3
3
16.06.2019
19

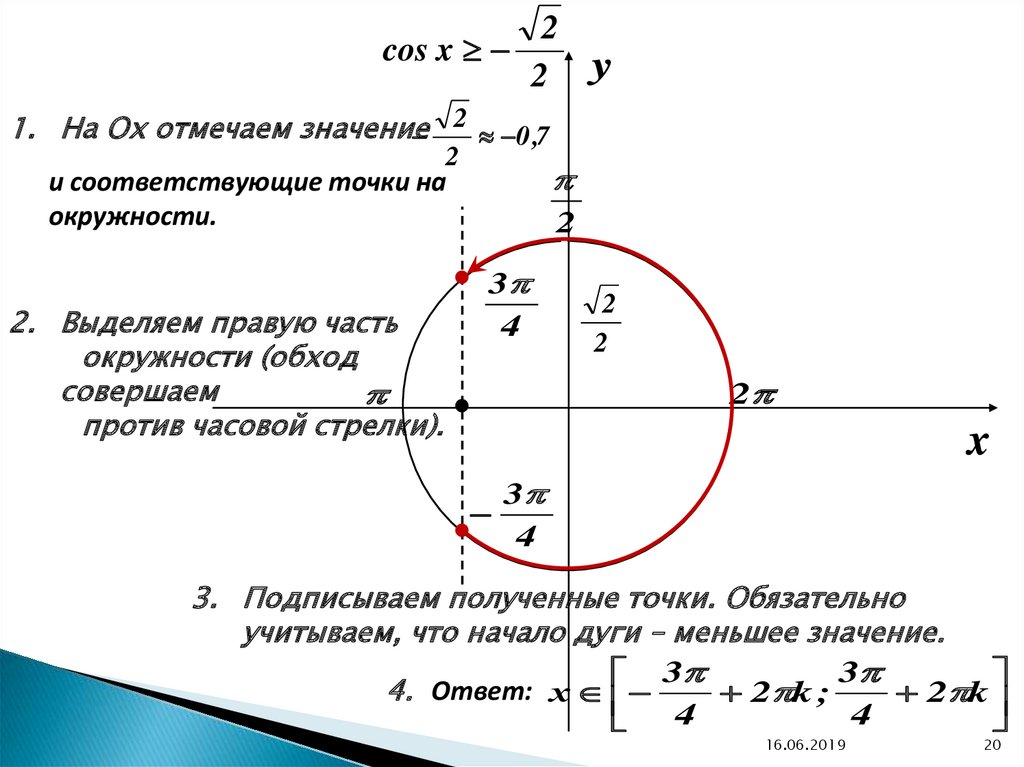
20.

cos x
2
2 y
2
1. На Ох отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2. Выделяем правую часть
окружности (обход
совершаем
против часовой стрелки).
2
3
4
2
2
2
x
3
4
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
3
3
4. Ответ: х
2 k ;
2 k
4
4
16.06.2019
20

21.

1. Перед контрольной работой я ещё
затрудняюсь при …
2. Я не очень уверенно выполняю задание на
нахождение …
3. Лучше всего у меня получается решение …
4. Мне нравится, что …

22. Домашнее задание: готовимся к контрольной работе

№16.32, №16.11(б),
№16.13(б),№16.18(б,в).