Моделирование сейшевых колебаний

1. Моделирование сейшевых колебаний

Выполнил: Швец П.А.
Научный руководитель: Павлова А.В.

2. Цель работы

– исследование
свободных линейных колебаний
однородной невязкой жидкости
в частично замкнутом бассейне,
имеющем одну открытую
границу.

3. Система уравнений длинных волн

u
w
g
x
t
v
w
g
y
t
w
hu hv
x
y
t

4. Решение краевой задачи в виде периодических по времени функций

u x, y,t u1 x, y e
i t
v x, y,t v1 x, y e
i t
w x, y,t w1 x, y e
i t

5. Задача

X X 0
X X 0
X 0 0
X 0 0
X a 0
X a 0
X X 0
X 0 0
X
a
0
Y Y 0
Y (0) 0
Y (b) 0

6. Собственные значения

( 2 n)
n
, n 1, 2,3...
2
4a
2
vn
n
2
b
2
2
, n Z

7. Собственные функции

2 n
X n Cn cos
x , n 1, 2,3...
2a
Yn cos
n
b
y, n Z

8. Частное решение

(1 2n) x
k y
wnk ( x, y ) Cnk cos
cos
2a
b

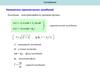
9. Формула для вычисления собственных чисел

(1 2k )
m
2a
b
2
km
/ gh
2
2
квадрат волнового числа

10. Итог

В работе поставлена задача о линейных колебаниях однородной невязкой жидкости в
частично замкнутом бассейне, имеющем одну открытую границу.
Уравнения эллиптического типа второго порядка с постоянными коэффициентами с
однородными граничными условиями решены, методом разделения переменных
(метод Фурье).
Построено аналитическое решение для бассейна прямоугольной формы,
имеющего постоянную глубину.