Similar presentations:
Построение графика функции
1.
Методическая разработка к урокуПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
y f x l ,
ЕСЛИ ИЗВЕСТЕН ГРАФИК ФУНКЦИИ
Дорошина Мария Викторовна
учитель математики и
информатики
МБОУ «Деминская основная
общеобразовательная школа»
2012 г.
y f x
2.
• Цель: Организовать деятельность учащихся поизучению и первичному закреплению знаний о
построении графиков функций y = f(x + l).
• Задачи:
• а) обеспечить восприятие, осознание, осмысление
учащимися того, какие преобразования позволят
построить графики функций y = f(x + l);
• б) способствовать развитию математической
компетентности у учащихся.
• в) воспитание рефлексивной культуры учащихся,
готовности к пересмотру своих суждений в свете
убедительных аргументов;
3.
График какой функцииизображен на рисунке?
4.
Уy = х2
1
0
1
Х
5.
У1
0
Х
1
y = – х2
6.
У1
у
х
1
0
1
Х
7.
У1
у
х
1
0
1
Х
8.
Уу
х
1
0
1
Х
9.
2yyy xxx
1
2
22
y
9
xx
-1
-4
0
-3
1
-2
2
-1
03
14
25
yy
9
4
1
0
4
1
4
2
9
-3 -2
-1 0
1
2
3
x
10.
Функцияy
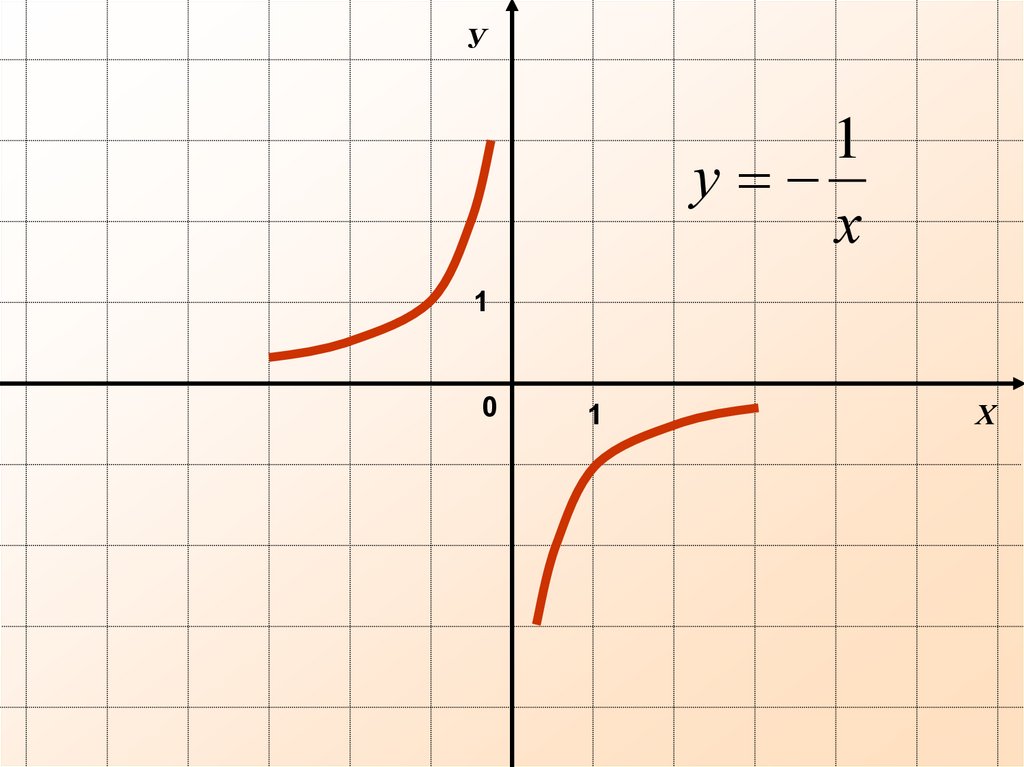
11
y
xx
32
8
4
-8
-4
2
1
-2 -1
0
x
1
-1 2
-2
-4
-8
4
8
11.
y=х2,
y = (х +
1)2
У
y = (х + 1)2
y = х2
0
Х
12.
y=х2,
y = (х –
1)2
У
y = (х – 1)2
y = х2
0
Х
13.
Первый способпостроения
сдвиг графика
14.
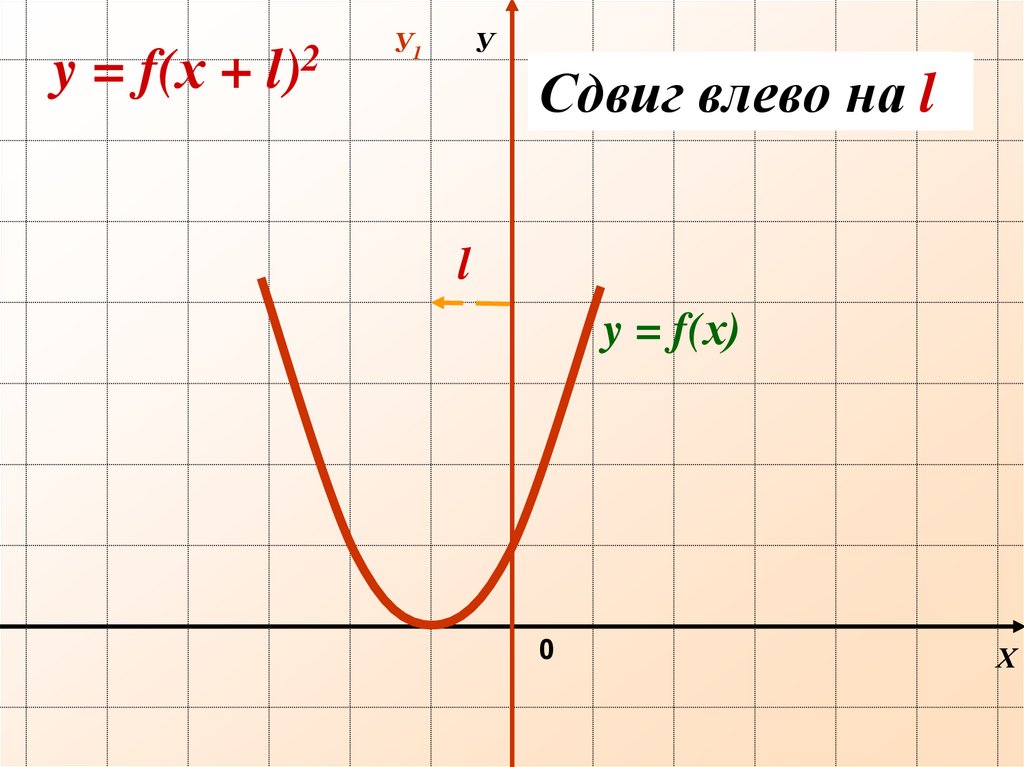
Уy = f(х + l)2
Сдвиг влево на l
l
l
l
y = f(х)
l
l
0
Х
15.
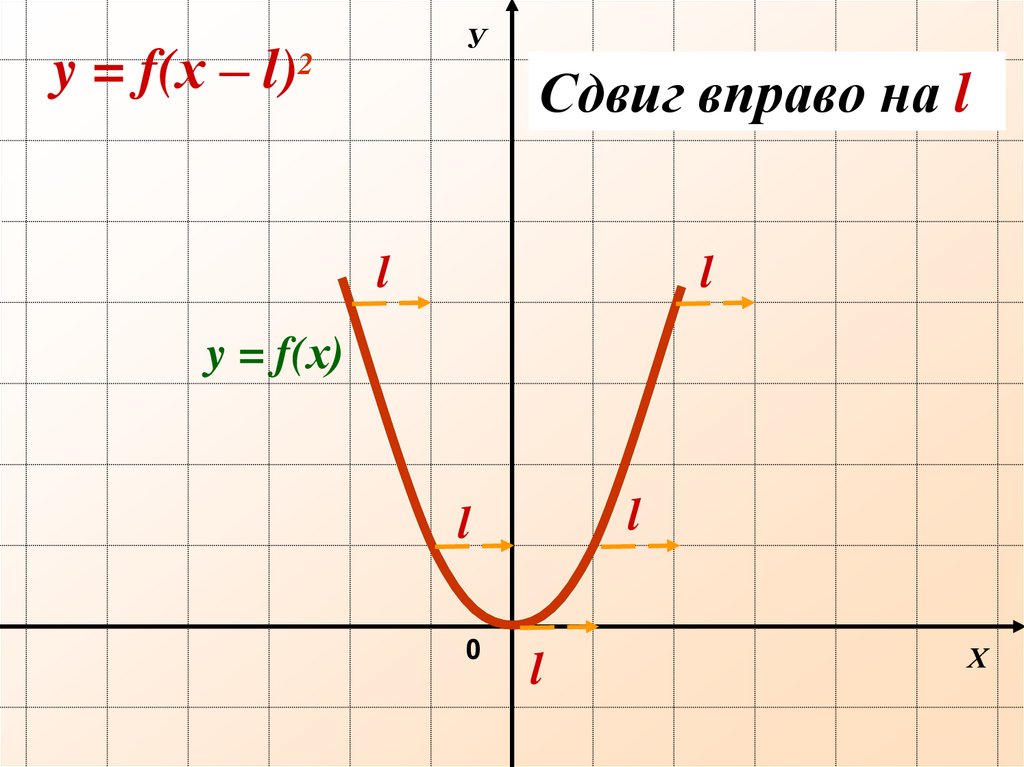
Уy = f(х – l)2
Сдвиг вправо на l
l
l
y = f(х)
l
l
0
l
Х
16.
Второй способпостроения
сдвиг оси координат
17.
y = f(х +l)2
У1
У
Сдвиг влево на l
l
y = f(х)
0
Х
18.
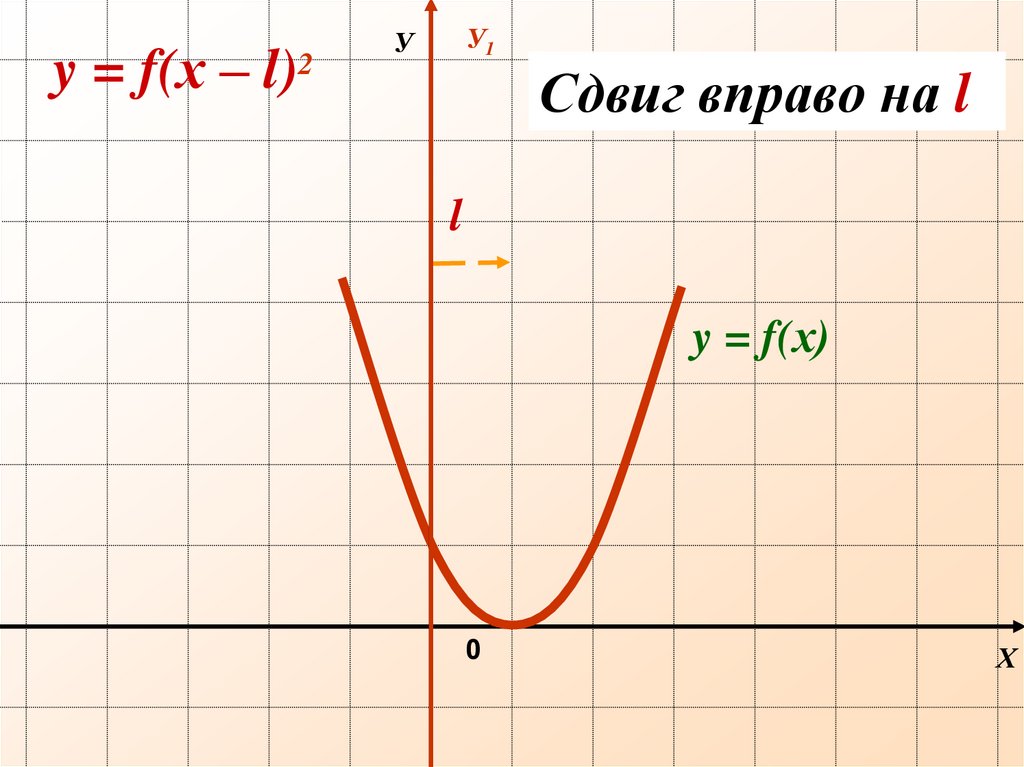
y = f(х – l)2У1
У
Сдвиг вправо на l
l
y = f(х)
0
Х
19. Преобразование:
y f (x l)Сдвиг по оси Оx.
l>0
y
y f (x l)
y f ( x)
x
l
Сдвиг по оси x влево
20. Преобразование:
Сдвиг по оси Оx.y f (x l)
l>0
y
y f ( x)
y f (x l)
x
l
Сдвиг по оси x вправо
21. Домашнее задание
• Учебник: § 19 стр. 107 – 110;• Задачник № 19.6, 19.7 – 19.10 (в,г), 19.22
стр. 116 – 119.
















 mathematics
mathematics








