Similar presentations:
Электротехника и электроника. Спектральный метод анализа электрических цепей. (Лекция 9)
1.
Кубанский государственный технологический университетИнститут информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 9
Спектральный метод анализа
электрических цепей
2.
Учебные вопросы:1.
Несинусоидальные колебания в электрических
цепях. Методы анализа.
2. Спектры типовых сигналов
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 234 – 249
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 103 –
117.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 37 –83.
4. Радиотехнические цепи и сигналы: Учебник для вузов, Под ред.
Самойло К.А.- М.: Высшая школа, 2002 г, с. 41 – 65.
3.
1. Несинусоидальные воздействия в электрических цепях. Методыанализа
В основе методов анализа и синтеза электрических цепей, находящихся
под воздействием периодических несинусоидальных и непериодических
токов и напряжений лежит спектральное представление
несинусоидальных воздействий, базирующееся на разложении в ряд
или интеграл Фурье.
1.1 Периодические воздействия
Из курса математического анализа известно, что всякая периодическая
функция f(t), удовлетворяющая условиям Дирихле (если функция f(t) на
периоде Т имеет конечное число разрывов первого рода и конечное число
максимумов и минимумов, что для реальных электрических сигналов обычно
выполняется сигналов), то она может быть разложена в ряд Фурье:
a0
2
f (t ) ak cos(k t ) bk sin( k t )
2 k 1
T
2
ak
T
T
f (t ) cos(k t )dt
0
Коэффициенты
разложения
2
bk
T
T
f (t ) sin(k t )dt
0
4.
TПредставляет собой среднее за период значение f(t)
f (t ) dt (функция f(t) может иметь смысл как тока, так и
0
напряжения) и называется постоянной составляющей.
составляющей
Таким образом, ряд Фурье показывает, что любая периодическая функция
f(t) может быть разложена на постоянную составляющую а0/2 и
совокупность гармонических колебаний составляющих гармоник Аmk с
кратными частотами:
a
a0
1
2
T
f (t )
Amk a b
2
k
2
k
0
2
Amk cos(k t k ),
k 1
Амплитуда k-й
гармоники
k arctg
bk
ak
ak Amk cos k
bk Amk sin k
Начальная фаза k-й
гармоники
В задачах анализа цепей при периодических воздействиях удобно
пользоваться комплексным рядом Фурье. Такой ряд
получится, если временную функцию
n-й гармоники записать,
используя формулу Эйлера, в виде суммы показательных функций:
(t ) ak cos(k t ) bk sin( k t )
5.
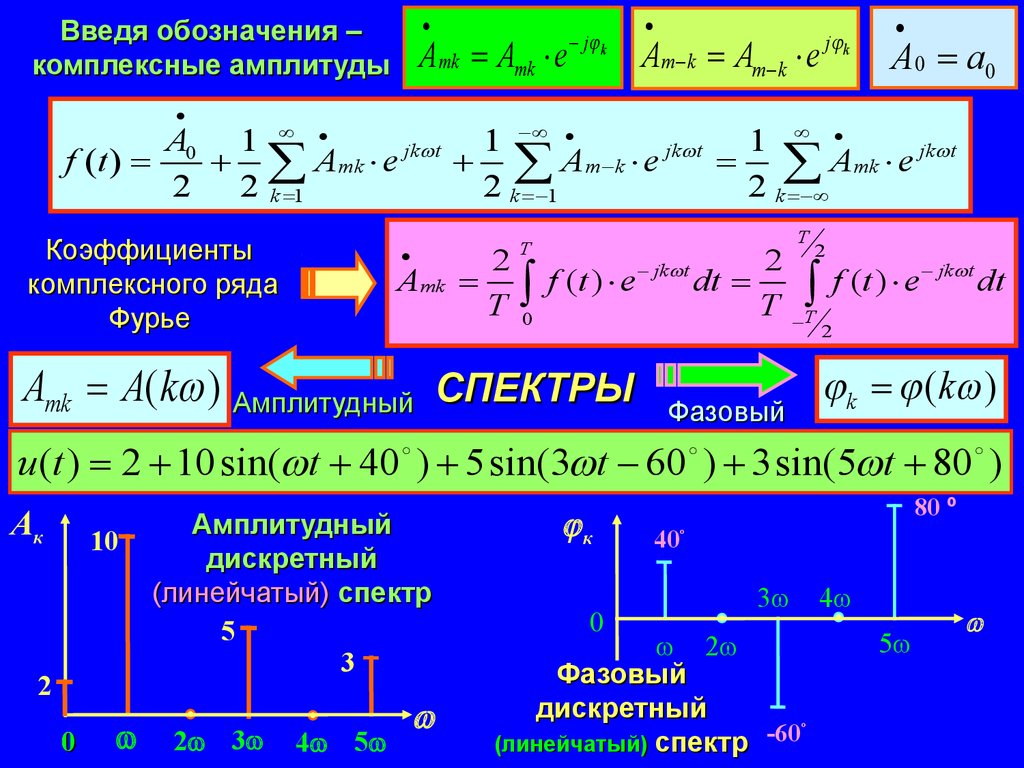
Введя обозначения –комплексные амплитуды
Amk Amk e
j k
j k
Am k Am k e
А 0 а0
A0 1
1
1
jk t
jk t
f (t )
Amk e
Am k e
Amk e jk t
2
2 k 1
2 k 1
2 k
Коэффициенты
комплексного ряда
Фурье
Amk
2
T
T
f (t ) e
jk t
0
Amk A(k ) Амплитудный СПЕКТРЫ
2
dt
T
T
2
T
Фазовый
f (t ) e jk t dt
2
k (k )
u (t ) 2 10 sin( t 40 ) 5 sin(3 t 60 ) 3 sin(5 t 80 )
Ак
10
2
0
Амплитудный
дискретный
(линейчатый) спектр
5
3
2 3 4 5
к
0
80 º
40º
3 4
2
Фазовый
дискретный
º
-60
(линейчатый) спектр
5
6.
1.2 Непериодические воздействияДля
непериодических
сигналов
используются
спектральные
представления, базирующееся на паре преобразований Фурье.
Фурье
f(t)
f (t )
f (t ) dt
Т
t1
0
t2
Т
1
2
f1 (t ) Amk e jk t , Amk
2 k
T
1
f1 (t )
2
T
Т
T
2
T
t
Т
f (t ) e jk t dt ; T
2
2
1
T
2
1 d
1
jk t
jk t
j t
e
1 f (t ) e
dt
f (t ) lim f1 (t )
e d f (t ) e jk t dt
T
2 T
k 1
k
T
2
F ( j )
2
1
1
2
f (t ) e
j t
dt
Преобразование Фурье
Прямое
Обратное
1
f (t )
2
j t
F
(
j
)
e
d
7.
Прямое и обратное преобразования Фурьесоставляют основу спектрального анализа сигналов
Спектральную плотность можно представить в показательной форме
F ( j ) F ( j ) e
j ( )
Модуль спектральной плотности
определяет
амплитудный спектр сигнала
F ( ) A2 ( ) B 2 ( )
A( )
f (t ) cos tdt
B( )
f (t ) sin tdt
F ( ) e
j ( )
Аргумент
спектральной
плотности определяет
фазовый спектр
( ) arctg
B( )
A( )
Вид модуля F( )=|F(j | позволяет судить о распределении энергии в
спектре непериодического сигнала, определяемом равенством
Парсеваля (теоремой Рэлея)
1
f (t )dt
2
2
2
F ( j ) d
1
2
F ( j ) d
0
В отличии от линейчатого (дискретного) спектра периодических сигналов
спектр непериодического сигнала носит сплошной характер (т.к. разность
между соседними частотными составляющими равная d бесконечно мала)
8.
Um2U m
U
2U m
2U m
k
u (t )
sin(
) cos k C t m
cos C t
cos 3 Ct
q
2
2
3
k 1 k
u(t)
T
T
U
q
m
-T/2
0
-T/2
0
-T/2
T/2
Перваягармоника
гармоника
u(t) Первая
0
u(t)
T/2
T/2
t
Третьягармоника
гармоника
Третья
t
t
9.
Свойства сигналов и их спектровДля сигналов f(t) и их спектров F(j ) справедлив ряд свойств:
n
a
k 1
n
k
f k (t ) ak Fk ( j )
свойство линейности
k 1
d
f (t ) j F ( j )
dt
дифференцирования сигнала
1
f (t ) dt
F ( j )
j
интегрирование сигнала
смещение сигнала по
времени на
f (t ) F ( j ) e j
Умножение спектров (теорема свертки)
F1 ( j ) F2 ( j ) f1 ( ) f 2 (t )dt f1 (t ) f 2 ( )dt
Ширина спектра сигнала увеличивается
1
j
при сжатии сигнала во времени
f (at ) F (
)
a
a
Изменение
масштаба
(уменьшении длительности сигнала) и наоборот,
уменьшается при растяжении
сигнала во времени.
10.
2. Спектры типовых сигналовДля теоретических и экспериментальных исследований характеристик
электрических цепей и передачи сообщений по каналам связи
используются различные типы сигналов: гармонические колебания,
уровни постоянных напряжений, последовательности прямоугольных
импульсов и т.п. Особо важную роль в теоретических исследованиях
играют испытательные сигналы в форме единичной функции 1(t) и
единичной импульсной функции (t) – функции Дирака
u(t)
Единичная функция
1
1(t) =
t
Обобщенное
преобразование
Фурье
Спектр
единичной
функции
u(t)
1, при t 0
1/
0, при t 0
F ( j , c) 1(t ) e
ct
e
j t
dt 1(t ) e
( c j ) t
t
1
dt
c j
1
1
1 j2
F ( j ) lim F ( j , c) lim
e
c
c 0 c j
j
11.
F(j )Фазовый
спектр
(j )
Амплитудный
спектр
0
- /2
Единичная импульсная функция
Эта
функция
является
нереализуемой
математической
абстракцией,
однако
обладает рядом интересных свойств и играет
важную роль в теоретических исследованиях.
0, при t 0
(t)= , при t 0
0, при t 0
Фильтрующее свойство (t) функции
Спектр
дельта
функции
f (t ) (t t )dt f (t )
0
0
F ( j ) (t ) e
j t
dt (t ) cos tdt j (t ) sin tdt 1e j 0 1
(t) функция имеет равномерный амплитудный и нулевой
фазовый спектры
12.
Спектр постоянной составляющейu(t)
2 ( )U
U
0
Обратное
преобразование
Фурье
t
1
(t )
2
e
j t
F(j )
0
d
1
( )
2
t
j t
e
dt
Спектр гармонического F ( j ) U m cos 0t e j t dt ,
колебания
U
F ( j ) m
2
u (t ) U m cos 0t
U
e j ( 0 t )t dt m
2
U m ( 0 ) ( 0 )
u(t)
Um
0
t
e j ( 0 t )t dt
F(j ) U
m
U m
- 0
0
0
13.
Спектр последовательности прямоугольных импульсовu(t)
Т
Um
И
И/2
И/2
Комплексная амплитуда k-й гармоники будет равна
И /2
T /2
2
2
2U m
jk t
jk t
jk t И / 2
u
(
t
)
e
dt
U
e
dt
e
/ И / 2
m
T T / 2
T И / 2
T j k
0
Am k
2U m
И
2
e
jk И
2
e
jk И
2
jk И
jk 2И
2
2U m И e
e
Т
2j
t
1
И
k
2
И
T j k
2
И
sin( k )
2U m
2U m sin x 2U m И sin x
И
2
, где x k
q
q
x
T
x
2
k И
2
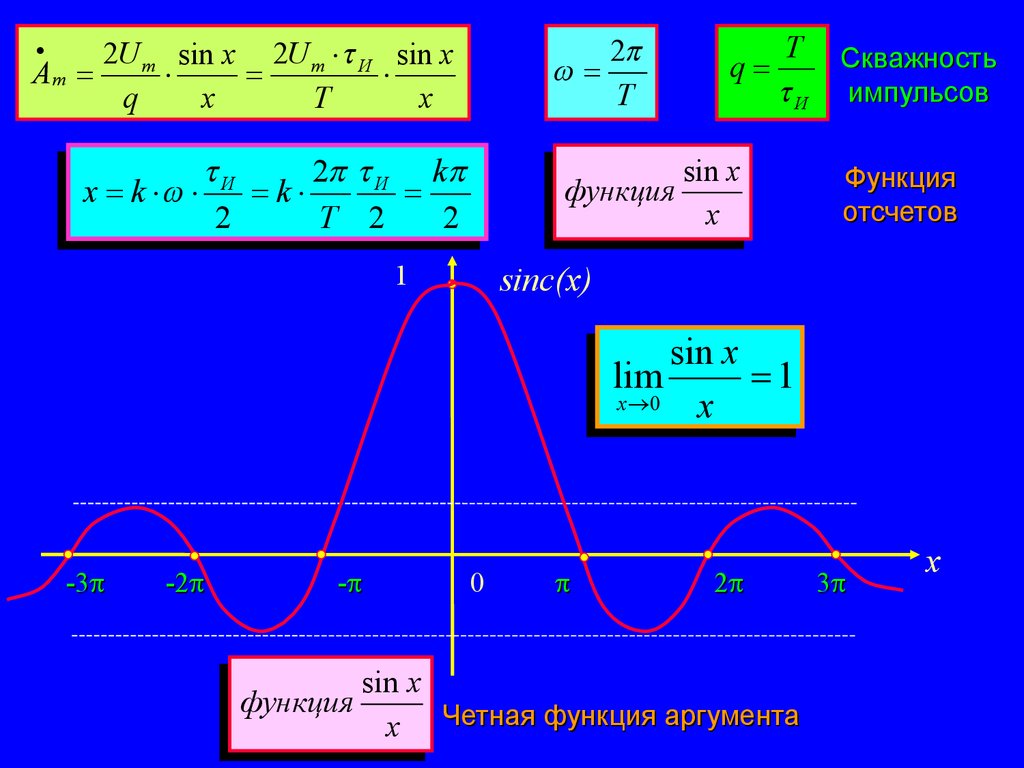
14.
2T
2U m sin x 2U m И sin x
Am
q
x
T
x
И
2 И k
x k
k
2
T 2
2
q
Т
И
sin x
функция
x
1
Скважность
импульсов
Функция
отсчетов
sinc(x)
sin x
lim
1
x 0
x
-3
-2
-
0
2
sin x
функция
x Четная функция аргумента
3
x
15.
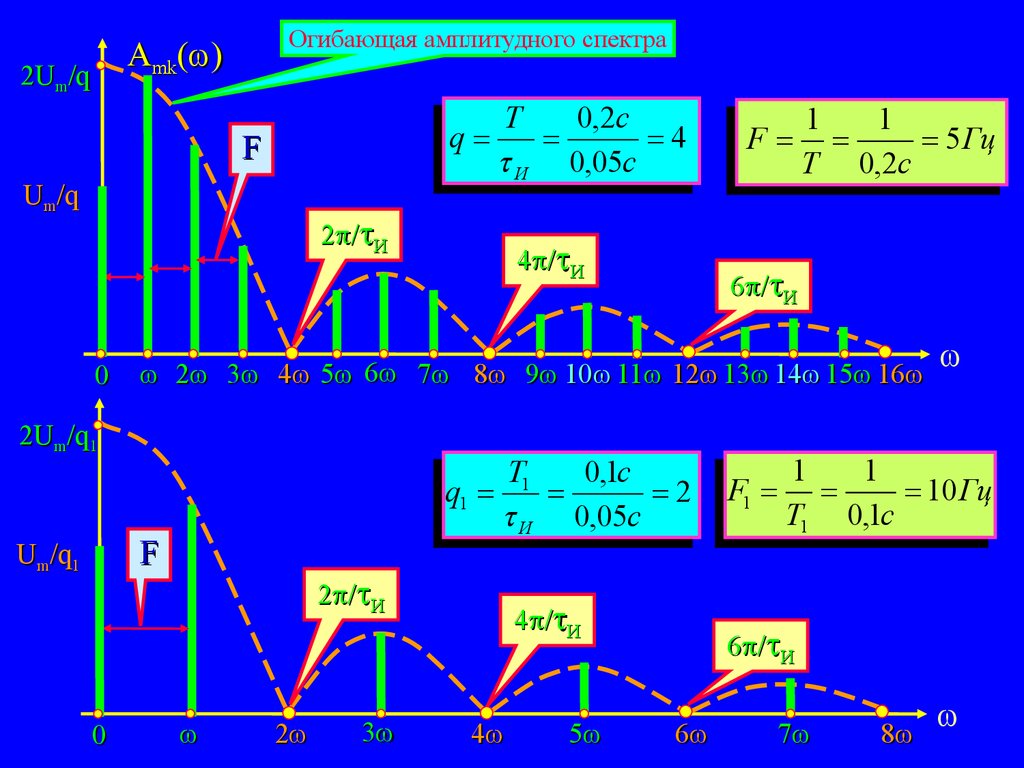
Огибающая амплитудного спектраAmk( )
2Um/q
q
F
Um/q
T
0,2с
4
И 0,05с
2 / И
0
T1
0,1с
q1
2
И 0,05с
F
0
6 / И
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2Um/q1
Um/q1
4 / И
1
1
F
5 Гц
T 0,2c
2 / И
2
3
4 / И
4
5
F1
1
1
10 Гц
T1 0,1c
6 / И
6
7
8
16.
Амплитудно-частотный спектр такой последовательности импульсовAmk
2 U m
q
sin( k
k
И
)
2
Огибающая
амплитудного
спектра
имеет много лепестков: первый из
которых занимает интервал частот от 0 до
(2 И), второй от (2 И) до 2·(2 И) и т.д.
И
2
Ширина каждого лепестка равна (2 И) и определяется только
длительностью импульса. Расстояние между спектральными линиями
равно F = 1/Т – частоте повторения импульсов, т.е. определяется периодом
импульсной последовательности.
Вид спектра периодической последовательности существенно зависит
от скважности импульсной последовательности – q = Т/ И
Узлы (нули) амплитудного спектра – значения частот k· , в которых Amk( ) =
0 и происходит смена знака сомножителей спектра, т.е. фаза скачком изменяется
2 И
на 180°.
sin( k И ) sin( k
) 0; sin( k ) 0; k n
2
T
2
q
Вывод:
Амплитудно-частотный
спектр
периодической
последовательности
прямоугольных импульсов является дискретным. Вид (огибающая) спектра
определяются формой импульса, структура спектра (количество спектральных
составляющих) - скважностью импульсной последовательности. На частотах
кратных скважности – спектральные составляющие отсутствуют,т.е. равны нулю.
17.
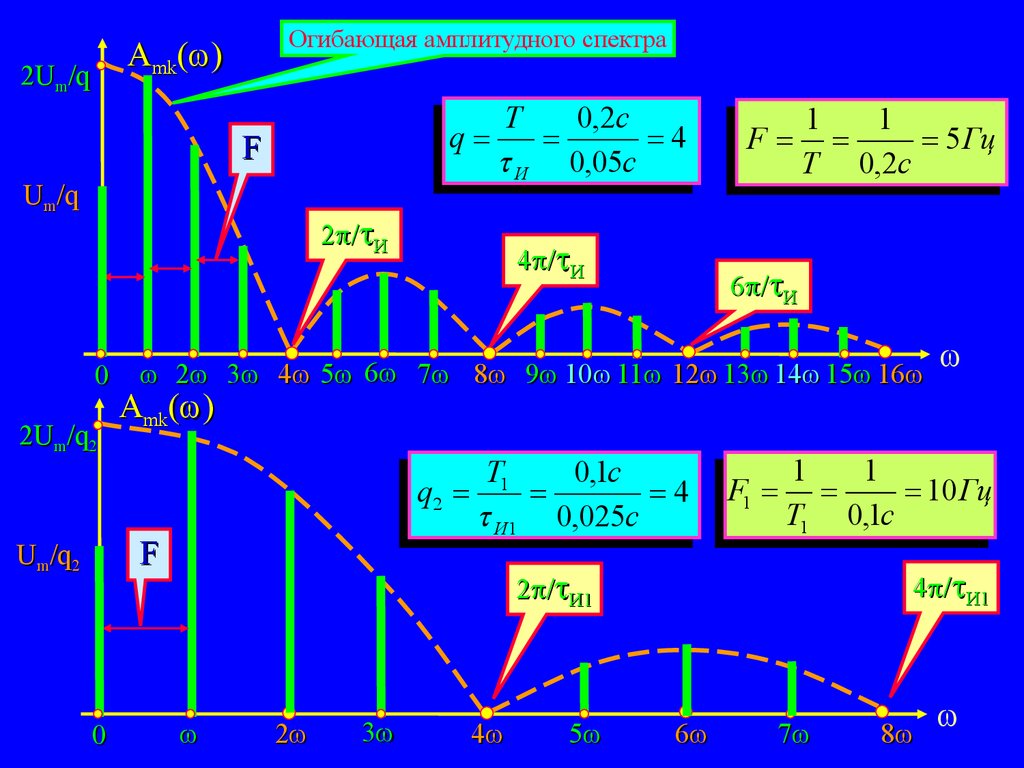
Огибающая амплитудного спектраAmk( )
2Um/q
q
F
Um/q
T
0,2с
4
И 0,05с
2 / И
0
2Um/q2
0
6 / И
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Amk( )
T1
0,1с
q2
4
И 1 0,025с
F
Um/q2
4 / И
1
1
F
5 Гц
T 0,2c
1
1
F1
10 Гц
T1 0,1c
4 / И1
2 / И1
2
3
4
5
6
7
8
18.
Спектр одиночного прямоугольного импульсаОпределим спектр (спектральную плотность)
u(t)
И
2
И
Um
И/2 0 И/2
t
j И
j И
U
F ( j ) U m e j t dt m (e 2 e 2 )
j
И
Um e
2
(
Um· И
2
j
И
2
e
2j
j
F(j )
F(j
2 / И
0
И
sin
sin x
2
) U m И
U m И
И
x
2
Огибающая cпектральной плотности
0,21SИМ
0,1F(0)
И
2
4 / И
0, 13SИМ
0, 09SИМ
6 / И
19.
Вид графика спектральной плотностиИ
sin( )
2
F ( j ) U m И
И
2
F ( 0)
Функция спектральной плотности обращается в
нуль при значениях аргумента · И /2 = n· .
Спектральная
плотность
импульса
произвольной формы при = 0 численно
равна его площади
j t
s
(
t
)
e
dt
j0
s
(
t
)
e
dt
s(t )dt S
ИМП
Вывод: Спектр (спектральная плотность) непериодических сигналов
является сплошным. Огибающая спектральной плотности
определяется формой импульса. Значение спектральной плотности
на нулевой частоте численно равно площади импульса. При
увеличении длительности импульса происходит сжатие спектра и
наоборот.
Распределение энергии в спектре
Распределение энергии в спектре
периодических сигналов
непериодических сигналов
2
0
N
A 1
PA
Amk ; 0,95
4 2 k 1
2 f
2
И
1
PA
2 f
2
F
( )d ; 0,95
0
20.
Задание на самостоятельную работуЛитература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 234 – 249
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 103 –
117.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 37 –83.
4. Радиотехнические цепи и сигналы: Учебник для вузов, Под ред.
Самойло К.А.- М.: Высшая школа, 2002 г, с. 41 – 65.
















 physics
physics electronics
electronics








