Similar presentations:
Электротехника и электроника. Электрические цепи при импульсном воздействии. (Лекция 12)
1.
Кубанский государственный технологический университетИнститут информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 12
Электрические цепи при
импульсном воздействии
2.
Учебные вопросы:1. Методы анализа ЭЦ, основанные на принципе суперпозиции. Связь
реакции и характеристики электрической цепи.
2. Дифференцирующие цепи
3. Интегрирующие цепи
4. Разделительные цепи
Литература:
Литература
1. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 103 –
112.
2. Гусев В.Г., Гусев Ю.М. Электроника и микропроцессорная техника:
Учебник для вузов, - М.: Высшая школа, 2004 г, с. 450 – 468.
3. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. Основы теории
электрических цепей: Учебник для вузов, - СПб.: Издательство «Лань» 2002 г,
с. 194 –202.
3.
1. Методы анализа ЭЦ, основанные на принципе суперпозиции.Связь реакции и характеристики электрической цепи.
Суть всех методов заключается в том, что
воздействие
разлагается на множество элементарных
воздействий;
затем отыскиваются реакции цепи на выбранные
элементарные воздействия;
полученные реакции суммируются.
Конкретные методы различаются между собой формой элементарных
воздействий, суммой которых представляется заданное воздействие
Воздействие
Х = ХК
ЭЦ
(Характеристики
ЭЦ)
Частотные
Временные
Операторные
Реакция
Y = YК
4.
Частотные методы анализа ЭЦЧастотные методы анализа ЭЦ чаще всего используются тогда, когда
нет необходимости искать функцию времени реакции ЭЦ, а
достаточно найти ее спектр (спектральное представление).
Воздействие s1(t) разлагается на бесконечное множество
гармонических составляющих. Распределение комплексных амплитуд
этих колебаний – спектральную плотность S1(j ) находят с помощью
прямого преобразования Фурье.
S 2 ( j ) S1 ( j ) K ( j )
S1 ( j ) s1 (t ) e j t dt
K ( j )
U ВЫХ ( j )
U ВХ ( j )
Комплексная частотная
характеристика цепи
Реакцию цепи определяют с помощью обратного
преобразования Фурье, осуществляющего
суммирование гармонических колебаний с s1 (t )
бесконечно малыми амплитудами
1
2
j t
S
(
j
)
e
d
1
5.
Частотные методы анализа чаще всего применяются при исследованиипрохождения звуковых сигналов через линейные цепи, когда об искажениях
сигнала судят по их спектральному представлению (спектру).
Условие неискаженной передачи сигналов через ЭЦ
Неискаженным сигналом на выходе ЭЦ считают такой сигнал, который
отличается от входного только амплитудой (масштабом) и сдвигом по
времени (форма сигнала остается неизменной)
s2 (t ) k s1 (t t0 )
s2(t)
s1(t)
ЭЦ
(t)
t0
задержка
S 2 ( j ) k S1 ( j ) e j t0
К( ) k
АЧХ- const
ФЧХ- линейна
S 2 ( j )
j t 0
K ( j )
k e
S1 ( j )
K ( ) e
j ( )
(t)
- t0
( ) t0
d
d
6.
Частотные характеристики реальных ЭЦ могут лишь приближаться кэтим идеальным характеристикам лишь в ограниченной полосе частот
(полосе пропускания)
АЧХцепи
цепи
АЧХ
S( ),K( )
1
0,707
АЧХцепи
цепи
АЧХ
Спектрвходного
входного
Спектр
сигнала
сигнала
S( ),K( )
1
0,707
1
2
Линейные(частотные)
(частотные)
Линейные
искаженияминимальны
минимальны
искажения
илиотсутствуют
отсутствуют
или
1
2
Линейные
Линейные(частотные)
(частотные)
искажения
искаженияочень
оченьбольшие
большие
(весьма
(весьмасущественные)
существенные)
7.
Временные методы анализа ЭЦВоздействие при этом представляется суммой сдвинутых по времени скачков
t
s1 (t ) s1 (0) 1(t ) 1(t x) s1/ ( x) dx
0
где s1/(x) - производная функции s(x) – величина скачка в момент времени t
= x равна s1/(x)·dx
Анализируемая цепь описывается временными характеристиками:
переходной
характеристикой,
импульсной
Определение №1. Переходной
характеристикой
h(t) ЭЦ называется
характеристикой
.
реакция цепи на единичный скачок 1(t) воздействия.
Определение №2. Импульсной характеристикой g(t) ЭЦ
называется реакция цепи на единичный импульс (дельта –
импульс) (t) воздействия.
1
d
g (t ) lim h(t ) h(t t И ) h(t ) h(0 ) (t )
t И 0 t
dt
И
t
h(t ) g (t )dt
0
8.
Для вычисления реакции ЭЦ пользуются интегралами Дюамеляtt
ss22((tt)) ss11((00)) hh((tt)) hh((tt xx)) ss1/1/((xx)) dx
dx
При известной
переходной
характеристике
цепи
00
tt
ss22((tt)) ss11((00)) hh((tt)) hh((xx)) ss1/1/((tt xx)) dx
dx
00
tt
ss2 ((tt)) ss1 ((tt)) hh((00)) gg((tt xx)) ss1 ((xx)) dx
dx
2
1
1
00
tt
ss2 ((tt)) ss1 ((tt)) hh((00)) gg((xx)) ss1 ((tt xx)) dx
dx
2
1
1
При известной
импульсной
характеристике цепи
00
Связь между частотной и импульсной характеристиками ЭЦ
КК((jj )) gg((tt)) ee
j t t
j
dt
dt
p = j
dt
КК((рр)) gg((tt)) ee dt
00
рtрt
9.
2. Дифференцирующие цепиiC(t)
E
UВХ(t)
C
R
dU C (t )
iC (t ) C
dt
Выходное напряжение
снимается с резистора
UВЫХ(t)
E
0,95E
0,63E
UC, U R
UC(t)
0,37E
UR(t)
2
3
t
dU C (t )
dU C (t )
u ВЫХ (t ) i R RC
dt
dt
С учетом того, что UC(t)=UВХ – UВЫХ , имеем
dUCC((tt))
dUВХВХ((tt)) dU
dUВЫХ
dU
dU
ВЫХ((tt))
uuВЫХ
ВЫХ((tt))
dt
dt
dt
dt
dt
dt
Ошибка
Полезный
Ошибка
Полезныйэффект
эффект
При правильном подборе величины ЭЦ осуществляет безошибочное
дифференцирование только в том случае, если на ее входе действует
напряжение, изменяющееся с постоянной скоростью (включая и нулевую).
10.
1Условие дифференцирования сигналов
0,1
Реакция цепи на прямоугольный импульс
C
iC(t)
E
UВХ(t)
R
tИ
UВЫХ(t)
Переходная характеристика
дифференцирующей цепи
tt
hhДЦ
(t ) exp( )
ДЦ (t ) exp( )
ttИИ/ / ==11
Эффект
Эффектдифференцирования
дифференцирования
ttИ/ / ==10
10(постоянная
(постояннаявремени
времени
И
ЭЦ
ЭЦдолжна
должнабыть
бытьмного
многоменьше
меньше
длительности
длительностиимпульса)
импульса)
Е
t
ttИИ/ / ==0,1
0,1
Е
t
Е
t
Е
t
-Е
11.
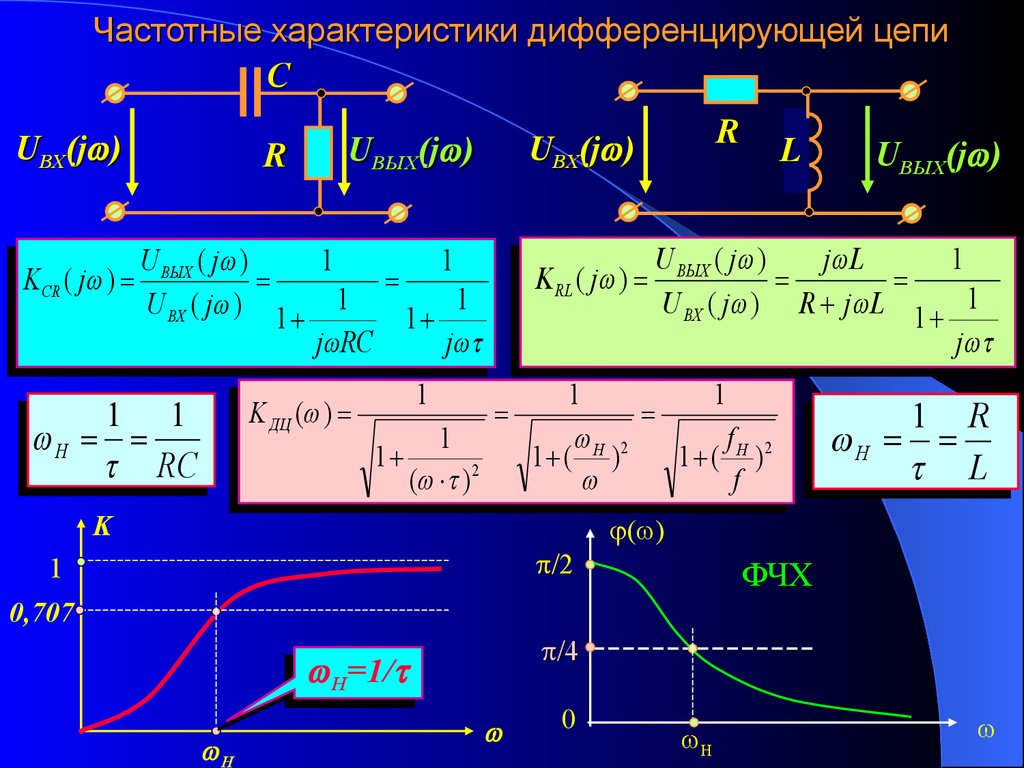
Частотные характеристики дифференцирующей цепиC
UВХ(j )
K СR ( j )
R
U ВЫХ ( j )
1
1
1
U ВХ ( j ) 1 1
1
j RC
j
K ДЦ ( )
1 1
Н
RC
1
1
1
( ) 2
R
UВХ(j )
UВЫХ(j )
K RL ( j )
/2
UВЫХ(j )
U ВЫХ ( j )
j L
1
U ВХ ( j ) R j L 1 1
j
1
1
Н 2
fH 2
1 ( )
1 ( )
f
K
1
L
1 R
Н
L
( )
ФЧХ
0,707
/4
=1/
НН=1/
Н
0
Н
12.
3. Интегрирующие цепиiC(t)
E
UВХ(t)
R
E
0,95E
UC, UR
UC(t)
0,63E
C
UВЫХ(t)
0,37E
UR(t)
t
1
uC (t ) iC (t )dt
C0
2
3
t
t
uC (t ) E (1 exp( ), при t 0
Если время интегрирования t много меньше постоянной времени цепи =
RC, то за время t напряжение uC(t) не успевает заметно измениться, и ток
iC(t) приблизительно пропорционален uВХ(t), а выходное напряжение
1
u ВЫХ (t ) uC (t )
C
t
t
t
1
1
i
(
t
)
dt
u
(
t
)
dt
uC (t ) dt
ВХ
0 C
RC 0
RC 0
Полезнаясоставляющая
составляющая
Полезная
интегрирования
интегрирования
Погрешность
Погрешность
интегрирования
интегрирования
t
13.
tt 11 tt 22
t
t
uuCC((tt))
E
E((11
exp(
exp(
))
E
E
(( ))
uuВЫХ
ВЫХ ((tt))
22
Условие интегрирования сигналов
1 10
E
Реакция цепи на прямоугольный импульс
iC(t) R
tИ
Е
UВХ(t)
C
UВЫХ(t)
ВЫХ
Эффект
Эффектинтегрирования
интегрирования
ttИ/ / ==0,1
0,1(постоянная
(постояннаявремени
времени
И
ЭЦ
ЭЦдолжна
должнабыть
бытьмного
многобольше
больше
длительности
длительностиимпульса)
импульса)
Переходная характеристика
интегрирующей цепи
t
t
11 exp(
exp( ))
hhИЦ
ИЦ((tt))
t
Е
Е
ttИИ/ / ==11
t
t
Е
ttИИ/ / ==10
10
t
14.
Интегрирование импульсной последовательностиУровень постоянной составляющей U0
UВХ(t)
tИ
Е
Т
t
UВХ(t)
Заряд «С»
Разряд «С»
u1mС (t ) U mВХ (1 exp(
tИ
t
) U mВХ
u1CОСТ (t ) U1C exp(
u 2 mС (t ) U 1ОСТ (U mВХ U 1ОСТ )(1 exp(
ttИИ 11
UU00 UUmmВХ UUmmВХ
ВХ Т
Т qq ВХ
tИ
tИ
)
)
Таким образом, напряжение на выходе интегрирующей
цепи равно среднему значению входного напряжения,
т.е его постоянной составляющей.
15.
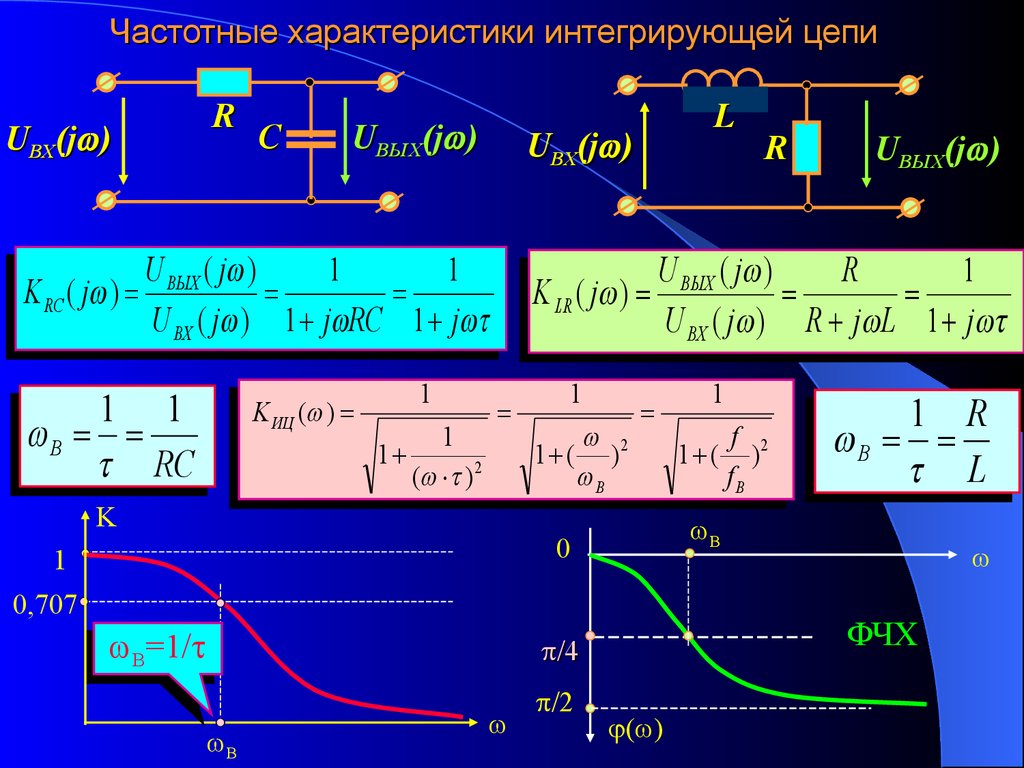
Частотные характеристики интегрирующей цепиUВХ(j )
R
C
UВЫХ(j )
UВХ(j )
1 1
В
RC
K ИЦ ( )
1
1
( ) 2
1
1 (
K
2
)
В
UВЫХ(j )
0,707
=1/
ВВ=1/
/2
1 (
f 2
)
fВ
1 R
В
L
ФЧХ
/4
1
В
0
1
В
R
U ВЫХ ( j )
R
1
K LR ( j )
U ВХ ( j ) R j L 1 j
U ВЫХ ( j )
1
1
K RС ( j )
U ВХ ( j ) 1 j RC 1 j
1
L
( )
16.
EC
U0
UВХ(t)
UВХ(t)
tИ
UC(t)
Е-U0
-U0
UR(t)
4. Разделительные цепи
Рассмотрим цепь по внешнему виду
как дифференцирующую, у которой
UВЫХ(t)
R
З Р RC
Е
t И
10
tИ
Уровень постоянной составляющей U0
Т
t
t
t
За счет разделительного конденсатора входное напряжение теряет
постоянную составляющую: напряжение на выходе цепи не содержит ее.
17.
Задание на самостоятельную работуЛитература:
Литература
1. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 103 –
112.
2. Гусев В.Г., Гусев Ю.М. Электроника и микропроцессорная техника:
Учебник для вузов, - М.: Высшая школа, 2004 г, с. 450 – 468.
3. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. Основы теории
электрических цепей: Учебник для вузов, - СПб.: Издательство «Лань» 2002 г,
с. 194 –202.















 physics
physics electronics
electronics








