Электротехника и электроника. Резонанс. Лекция № 7

1.

Кубанский государственный технологический университет
Институт информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 7
Резонанс
в электрических цепях

2.

Учебные вопросы:
1.
Резонанс напряжений. Параметры и частотные
характеристики колебательного контура.
2. Резонанс токов. Параметры и частотные характеристики
колебательного контура.
контура
3. Полоса пропускания колебательного контура.
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 105 – 113
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 54 – 66.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 37 –83.

3.

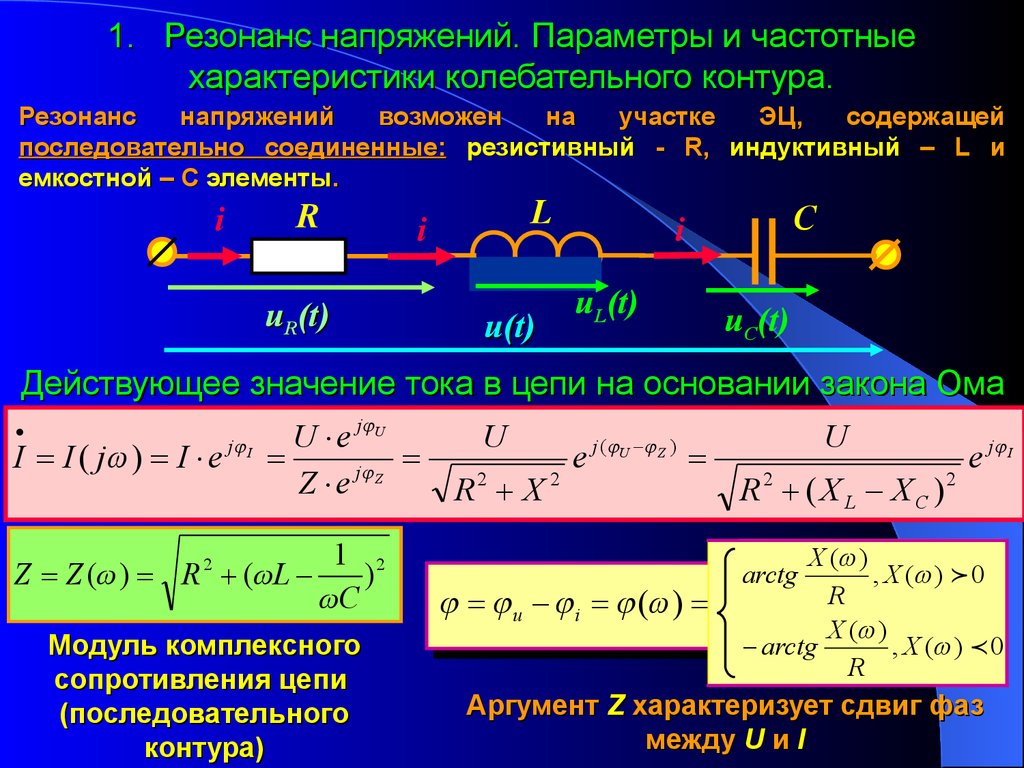
1. Резонанс напряжений. Параметры и частотные
характеристики колебательного контура.
Резонанс
напряжений
возможен
на
участке
ЭЦ,
содержащей
последовательно соединенные: резистивный - R, индуктивный – L и
емкостной – С элементы.
i
R
uR(t)
i
L
u(t)
С
i
uL(t)
uС(t)
Действующее значение тока в цепи на основании закона Ома
j U
U
e
U
U
j ( U Z )
j I
j I
I I ( j ) I e
e
e
Z e j Z
R2 X 2
R 2 ( X L X C )2
Z Z ( ) R 2 ( L
1 2
)
C
Модуль комплексного
сопротивления цепи
(последовательного
контура)
u i ( )
X ( )
, X ( ) 0
R
X ( )
arctg
, X ( ) 0
R
arctg
Аргумент Z характеризует сдвиг фаз
между U и I

4.

Режим
работы
неразветвленного
участка
цепи,
содержащей
последовательно соединенные резистивный - R, индуктивный – L и
емкостной – С элементы, при котором ее ток и напряжение
совпадают по фазе называется резонансом напряжений
I I ( )
U
Z ( )
U
R (X L XC )
2
2
U
R 2 ( L
1 2
)
C
max?
=0
= L –1/ C = 0, что может
быть выполнено лишь для некоторой частоты = 0. В этом случае
1
U
0 L
02 LC 1
I 0 I ( 0 ) I max var L, C или
0C
R
При резонансе = 0, если Х = ХL – XC
В последовательном контуре из токов с различными частотами выделяется ток,
только одной определенной частоты
Частота
входного
напряжения
при
которой
наступает
резонанс,
обозначается 0 и называется резонансной или собственной
частотой последовательного колебательного контура.
1
1
0
или f 0
L C
2 LC

5.

Реактивные сопротивления контура на частоте 0 равны друг другу.
Характеристическое
1
L
X L ( 0 ) X C ( 0 ) 0 L
Ом (волновое) сопротивление
0C
C
контура
Резонансные свойства
(избирательность) контура
Q
R
или
d
1
Q
Пример: Пусть U= 12 В, XL( 0) = XC( 0) = 500 Ом, R = 6 Ом.
Значение тока на
U C 0 I 0 X C ( 0 ) U L 0 I 0 X L ( 0 )
U 12
2A
резонансной частоте I 0
R 6
2 500 1000 B
U R 0 I 0 R 2 6 12 B, т.е. U C 0 U L 0 U R 0
Физический смысл
добротности
U L 0 U C 0 I 0 0 L
I0
U
U
U
U 0C
L
Q
C R R
Добротность показывает, во сколько раз резонансные
напряжения на реактивных элементах превышают приложенное
напряжение (напряжение источника входного сигнала) термин
«резонанс напряжений»

6.

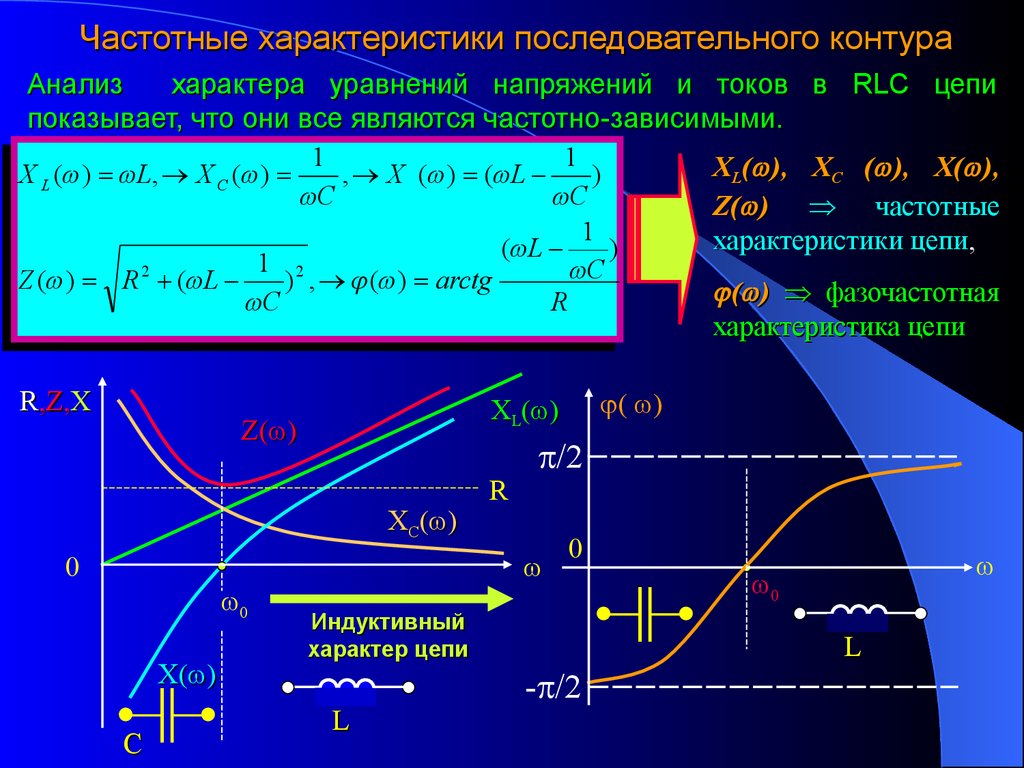
Частотные характеристики последовательного контура
Анализ
характера уравнений напряжений и токов в RLC цепи
показывает, что они все являются частотно-зависимыми.
1
1
XL( ), XC ( ), X( ),
X L ( ) L, X C ( )
, X ( ) ( L
)
C
C
Z( ) частотные
1
характеристики цепи,
цепи
( L
)
1 2
C
Z ( ) R 2 ( L
) , ( ) arctg
( ) фазочастотная
C
R
характеристика цепи
R,Z,X
Z( )
XС( )
0
0
X( )
С
( )
XL( )
R
/2
0
Индуктивный
характер цепи
L
0
L
- /2

7.

Рассмотрим частотные зависимости действующих значений тока в цепи и
напряжений на реактивных элементах контура.
U
I ( )
Z
U
;
R 2 ( L
U L ( ) I ( ) X L ( )
1 2
)
C
U L
R 2 ( L
U L ( ) I ( ) X C ( )
I 0 I max
max
U
, при 0
R
Экстремумы на частоте
1 2
)
C
;
U
1 2
C R 2 ( L
)
C
max
;
max
L0 0
1
0
1
1
2Q 2
С 0 0 1 1
2Q 2
0
Зависимости I( ), UL ( ), UC ( ) – называются амплитудно-частотными
характеристиками (АЧХ)
относительно тока и напряжений, или
резонансными характеристиками.
Для нахождения экстремумов UL ( ), UC ( ) необходимо:
U L ( )
0
U C ( )
0

8.

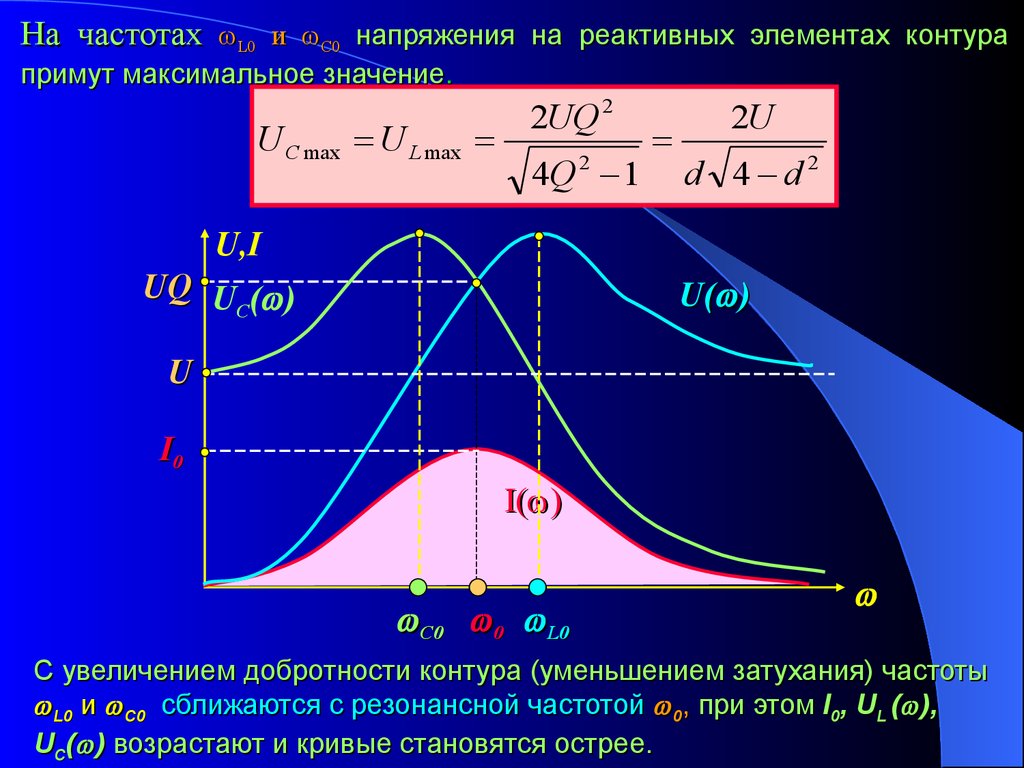
На частотах L0 и С0 напряжения на реактивных элементах контура
примут максимальное значение.
U C max U L max
2UQ 2
4Q 1
2
2U
d 4 d2
U,I
UQ U ( )
C
U( )
U
I0
I( )
C0 0 L0
С увеличением добротности контура (уменьшением затухания) частоты
L0 и С0 сближаются с резонансной частотой 0, при этом I0, UL ( ),
UC( ) возрастают и кривые становятся острее.

9.

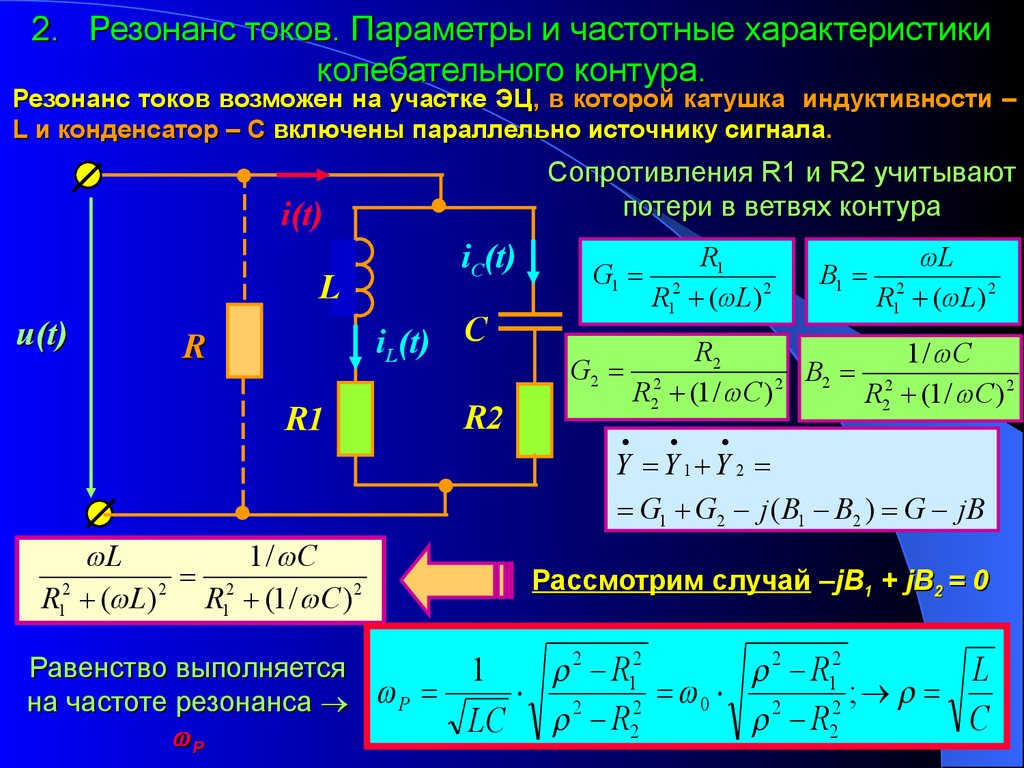
2. Резонанс токов. Параметры и частотные характеристики
колебательного контура.
Резонанс токов возможен на участке ЭЦ, в которой катушка индуктивности –
L и конденсатор – С включены параллельно источнику сигнала.
Сопротивления R1 и R2 учитывают
потери в ветвях контура
i(t)
L
u(t)
iC(t)
iL(t) С
R
R1
R2
G1
G2
R1
R12 ( L) 2
В1
L
R12 ( L) 2
R2
1 / С
В
R22 (1 / С ) 2 2 R22 (1 / С ) 2
Y Y 1 Y 2
G1 G2 j ( B1 B2 ) G jB
L
1 / C
R12 ( L) 2 R12 (1 / C ) 2
Равенство выполняется
на частоте резонанса
Р
Рассмотрим случай –jB1 + jB2 = 0
1
2 R12
2 R12
L
P
2 2 0 2 2 ;
R2
C
LC R2

10.

P
1
2 R12
2 R12
L
;
0
2 R22
2 R22
C
LC
Условие резонанса
R1 < , R2 < или R1 > , R2 >
Реактивные составляющие токов при резонансе равны друг другу
I P1 U B1 I P 2
L
1 / C
U B2 U 2
U 2
2
R1 ( L)
R1 (1 / C ) 2
R0Э – эквивалентное
I 0 U G0 Э
резонансное
сопротивление контура
Режим работы участка цепи с параллельными ветвями, при котором ток в
неразветвленной части и напряжение на выводах контура
совпадают по фазе называется резонансом токов
При этом эквивалентное резонансное сопротивление параллельного контура
U
R0 Э
Ток в неразветвленной
части цепи
R0 Э
2 R1 R2
R1 R2
Наибольший теоретический и практический интерес представляют резонанс
токов в контурах без потерь (R1 = R2 = 0) и с малыми потерями (R1 << , R2 << )

11.

Контур без потерь (R1 = R2 = 0)
Р 0
Уравнение резонансной частоты
1
LC
Эквивалентное сопротивление контура без потерь R0Э = и входной ток
равен нулю, а добротность обращается в бесконечность.
Комплексные действующие значения токов в ветвях контура:
U
U j 2
I1
e
j 0 L
U j 2
I 2 Uj 0C e
Контур с малыми потерями (R1 << , R2 << )
Р 0
Токи в
контуре
1
LC
при
условии
U
U
I0
2
R0 Э Q R
U
U
I1 I 2
QR
R1 R2
2
2
2
R0 Э
Q 2 R
R1 R2 R
U
U j 2
I1
e
j 0 L
I1 I 2 U /(Q 2 R )
Q
I 0 I 0 U /(Q R )
U j2
I 2 Uj 0C e
Отсюда и название
резонанс токов

12.

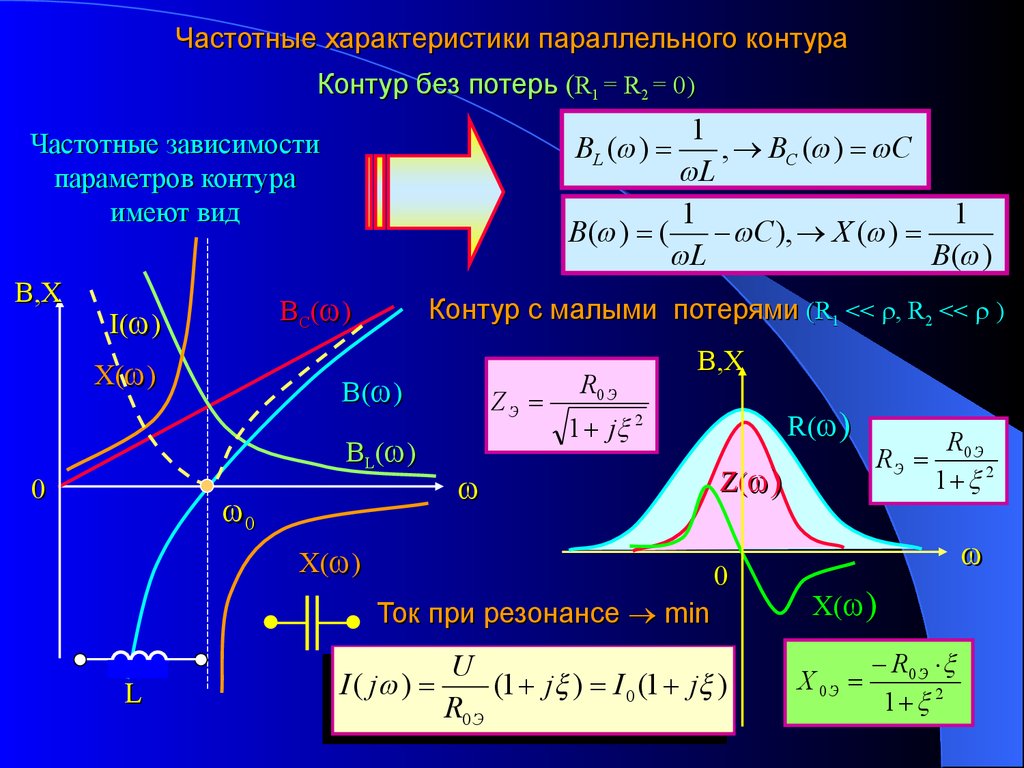
Частотные характеристики параллельного контура
Контур без потерь (R1 = R2 = 0)
1
, BC ( ) C
L
1
1
B ( ) (
C ), Х ( )
L
B( )
BL ( )
Частотные зависимости
параметров контура
имеют вид
В,Х
ВС( )
I( )
X( )
Контур с малыми потерями (R1 << , R2 << )
В( )
ВL( )
0
0
ZЭ
R0 Э
В,Х
R( )
1 j 2
X( )
Z( )
0
Ток при резонансе min
L
U
I ( j )
(1 j ) I 0 (1 j )
R0 Э
RЭ
R0 Э
1 2
Х( )
Х 0Э
R0 Э
1 2

13.

В реальном параллельном колебательном контуре резонансные
избирательные характеристики зависят от соотношения сопротивления
контура ZВХ(ω) и внутреннего сопротивления RИ источника
входного сигнала
Сопротивление контура ZВХ(ω)
RИ i(t)
совместно с внутренним
I(ω)
iC(t)
сопротивлением источника RИ
L
еИ
образуют делитель напряжения
ω i (t)
С
L
1) При RИ > ZВХ(ω)
Е(ω)
Z (ω)
R ВХ
UK(ω)
ω
I ( )
eИ
e
И const
RИ Z ВХ ( ) RИ
eИ
Z ВХ ( )
мал
U K ( )
Z ВХ ( ) var K ДН ( )
RИ
RИ
ω0
ω
Необходимо
усиление UK(ω)

14.

2) При RИ ZВХ(ω)
RИ
I(ω)
i(t)
L
еИ
ω0
Е(ω)
iC(t)
UK(ω)
UK(ω)
ω i (t)
С
L
ZВХ(ω)
UK(ω) =EИ =const
R
ω
eИ
eИ
I ( )
var
RИ Z ВХ ( ) Z ВХ ( )
eИ
U K ( )
Z ВХ ( ) eИ const
Z ВХ ( )
Избирательности
входного сигнала нет
ω
Параллельный
колебательный
контур включают в
цепи, обладающие
RИ Z ВХ ( )

15.

3. Полоса пропускания колебательного контура.
Избирательностью называется способность колебательного контура выделять
сигналы заданной частоты и уменьшать (подавлять) сигналы всех других частот .
Контур с лучшей избирательностью обладает большей добротностью
Избирательность характеризуется формой амплитудночастотной характеристики (АЧХ) контура
Полосой пропускания называется область частот, вблизи резонансной
частоты, в пределах которой напряжение (ток, модуль коэффициента
передачи) уменьшается в заданное число раз (чаше всего в 2 раз).
Последовательный колебательный контур
Нормированная АЧХ (UВЫХ = UC)
K( f )
1
1
KU
K ( f0 )
1 (2Q f / f 0 ) 2
1 2
Полоса
пропускания
1
K
Q1 > Q2 > Q3
0,707
Q2
f0 f0 R
2 f
Гц
Q
f 0 f 0 ( R RН )
f 0 ( R Ri )
2 f
Q
Q1 Q3
2 f3
f0
f

16.

Параллельный колебательный контур
1
X L C 0 L 0
( ) Q( 0 )
R
R
R 0
0
Обобщенная расстройка
Полоса пропускания параллельного контура определяется выражением :
fР
fР
2 f
QЭ QЭ
f 0 (1
R0 Э
Ri
)
Q
Q
, Q ; QЭ
R
R
1 0Э
R
i
1
K(f)
QЭ2
0,707
K( f )
UK
1
1
0,707
2
2
U KP
2
1 QЭ ( 0 )
Граничные частоты
QЭ1>QЭ2
f1, 2
QЭ1
f1
f0
f2
f
f0
( 1 4QЭ2 1)
2QЭ
2 f f 2 f1

17.

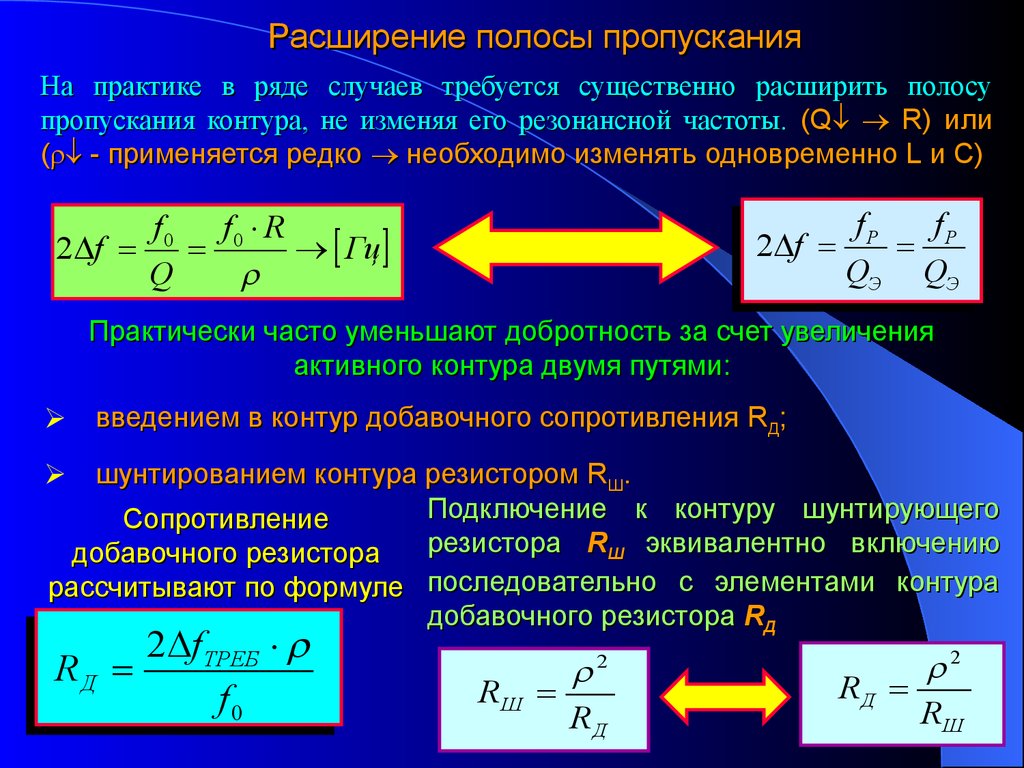
Расширение полосы пропускания
На практике в ряде случаев требуется существенно расширить полосу
пропускания контура, не изменяя его резонансной частоты. (Q R) или
( - применяется редко необходимо изменять одновременно L и С)
f0 f0 R
2 f
Гц
Q
fР
fР
2 f
QЭ QЭ
Практически часто уменьшают добротность за счет увеличения
активного контура двумя путями:
введением в контур добавочного сопротивления RД;
шунтированием контура резистором RШ.
Подключение к контуру шунтирующего
Сопротивление
резистора RШ эквивалентно включению
добавочного резистора
рассчитывают по формуле последовательно с элементами контура
добавочного резистора RД
2 f ТРЕБ
RД
f0
RШ
2
RД
2
RД
RШ

18.

Задание
на самостоятельную работу
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы
теории цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г,
с. 105 – 113
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории
электрических цепей и электроники: Учебник для вузов, - М.:
Радио и связь, 1999 г, с. 54 – 66.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для
вузов, - М.: Высшая школа, 2003 г, с. 37 –83.