Similar presentations:
Колебательные процессы
1. Колебательные процессы.
Свободные гармонические колебания. Дифференциальноеуравнение гармонических колебаний.
2. Основные понятия Колебательные процессы широко известны в природе и технике. Природа колебаний и сам колеблющийся объект могут
быть различны:температура, атомы твердого тела, центр тяжести маятника,
электрическое и магнитное поля и т.д. Среди них особое место занимают
механические колебания. К данному виду колебаний можно отнести
движение маятников, струн, мембран телефонов, поршней двигателей
внутреннего сгорания, мостов и других сооружений, подвергнутых
действию переменной силы.
Механическим колебанием называется процесс, при котором
характеристики движения принимают одни и те же значения через
некоторые промежутки времени. Колебания, при которых значения
физических величин, описывающих данный процесс, повторяются через
равные промежутки времени называются периодическими.
Минимальное значение этого промежутка времени
называется периодом колебаний.(T)
.
3.
• Гармонические колебания. Гармоническими называютколебания, при которых какая-либо физическая величина,
описывающая процесс, изменяется со временем по закону
косинуса или синуса:
(t) = Acos( 0t + ).
(1)
Константа A называется амплитудой колебания. Амплитуда это
наибольшее значение, которое может принимать колеблющаяся
величина. Согласно определению, она всегда положительна. Выражение
t + , стоящее под знаком косинуса, называют фазой колебания.
Она позволяет рассчитать значение колеблющейся величины в любой
момент времени. Постоянная величина представляет собой
значение фазы в момент времени t = 0 и поэтому называется
начальной фазой колебания. Значение начальной фазы зависит от
выбора начала отсчёта времени. Величина получила название
циклической частоты, физический смысл которой связан с
понятиями периода и частоты колебаний.
Периодом незатухающих колебаний называется наименьший
промежуток времени, по истечении которого процессы повторяются,
или время одного полного колебания. Число колебаний, совершаемых в
единицу времени, называют частотой колебаний. Частота n связана с
периодом T колебаний соотношением
n =1/T.
= 2 /T = 2 n.
Из этого соотношения следует физический смысл циклической
частоты. Она показывает, сколько колебаний совершается за 2 секунд.
4.
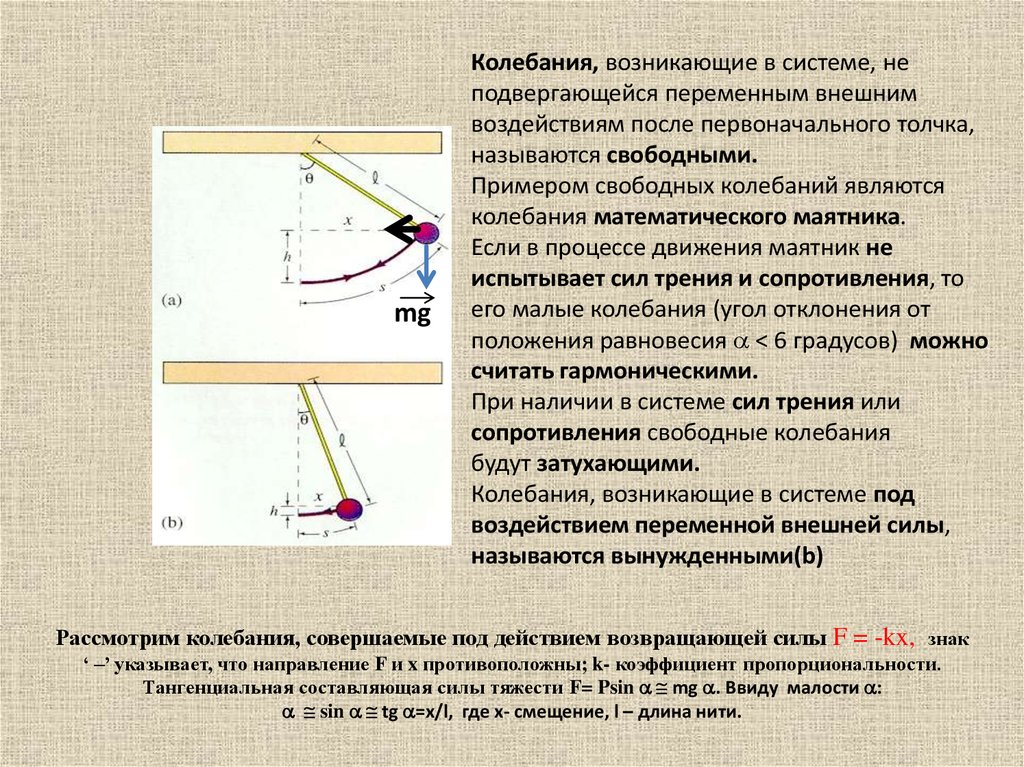
mgКолебания, возникающие в системе, не
подвергающейся переменным внешним
воздействиям после первоначального толчка,
называются свободными.
Примером свободных колебаний являются
колебания математического маятника.
Если в процессе движения маятник не
испытывает сил трения и сопротивления, то
его малые колебания (угол отклонения от
положения равновесия < 6 градусов) можно
считать гармоническими.
При наличии в системе сил трения или
сопротивления свободные колебания
будут затухающими.
Колебания, возникающие в системе под
воздействием переменной внешней силы,
называются вынужденными(b)
Рассмотрим колебания, совершаемые под действием возвращающей силы F = -kx, знак
‘ –’ указывает, что направление F и x противоположны; k- коэффициент пропорциональности.
Тангенциальная составляющая силы тяжести F= Psin mg . Ввиду малости :
sin tg =x/l, где x- смещение, l – длина нити.
5.
F=mУравнение второго закона Ньютона
для возвращающей силы F:
a
(2),aгде m – масса колеблющейся точки,
– ускорение.
d2x
a= 2 ,
dt
d 2 x k x = 0,
dt 2 m
d2x
m 2 = kx ,
dt
Введем обозначения
2
0
k
= ,
m
(3)
(*),
2
получим
d x 2
x
=
0
,
0
2
dt
(3*)
Получили дифференциальное уравнение свободных гармонических
колебаний , совершаемых под действием упругой или квазиупругой силы
при отсутствии сил сопротивления.
6.
Рассмотрим свободные незатухающиеэлектрические колебания в цепи.
Электрическую цепь, состоящую из индуктивности и ёмкости,
называют колебательным контуром (рис. 2). Электрическим
сопротивлением контура пренебрегаем (R = 0). Для установления
характера процессов, возникающих в контуре после зарядки
конденсатора,
надо
составить
дифференциальное
уравнение,
используя второе правило Кирхгофа. Согласно этому правилу, запишем
s = uс ( s — э. д. с. самоиндукции, uc — напряжение на конденсаторе).
Но
uс = q/C, где q и C заряд и ёмкость конденсатора, а
Здесь L - индуктивность соленоида, i - сила тока в контуре. С учётом этого
L
C
R
Рис. 2
di
s = L .
dt
di
L = q/C
dt
7.
di = d dq = d 2q .dt dt dt dt 2
i = dq
dt
L di q / C = 0.
dt
Учитывая это и разделив обе части последнего уравнения на L(индуктивность), получаем
d 2q 1 q = 0.
LC
dt 2
Отсюда
(4)
d 2q 2q = 0.
0
dt 2
Введем обозначения
02 = 1 / ( LC).
(4*)
С точки зрения математики уравнения (3) и (4) одинаковые. Их можно записать в виде:
d 2ξ ω2ξ = 0,
0
dt 2
(5)
где в случае маятника = x
и для эл. колебательного контура = q
2
0
2
0
=k/m
= 1 /( LC).
8.
Из теории дифференциальных уравнений известно, что данноеуравнение представляет собой дифференциальное уравнение
второго порядка с постоянными коэффициентами. Для его
решения надо составить характеристическое уравнение и
решить его: r 2 02 = 0.
Отсюда r = 0 . и
мнимая единица.
2
2
r = 02 = 0 1 = i 0, где -
i = 1,
Решением этого дифференциального уравнения будет выражение:
(t) = Acos( 0t + ).
(1)
8
9.
СКОРОСТЬ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ= dx = d [ Xmcos(ω0t + α)]= ω0 Xmsin(ω0t α),
dt dt
= mcos(ω0t + α ),
2
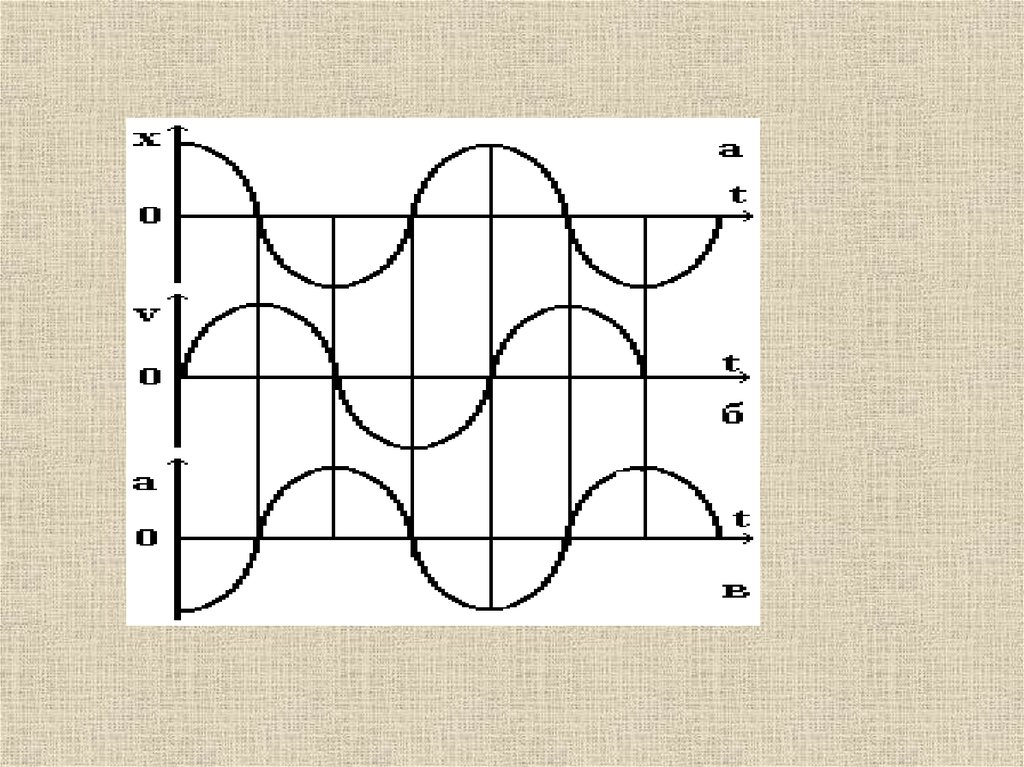
Вывод: Скорость м.т. при колебательных процессах изменяется по
гармоническому закону и является функцией времени.
10.
УСКОРЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙd d 2
a = = [ X mcos(ω0t + α)] = ω2 X mcos(ω0t α ),
0
dt dt
a = amcos(ω0t α ),
Вывод: Ускорение изменяется по гармоническому закону, является функцией
времени и опережает колебания смещения по фазе на и опережает колебание
скорости по фазе на /2.
11.
12.
СИЛА ТОКА И НАПРЯЖЕНИЕ В КОЛЕБАТЕЛЬНОМ КОНТУРЕq = qmcos(ω0t + α),
q
Uc = m cos(ω0t + α) = Umcos(ω0t α),
C
dq
i = = d [qmcos(ω0t + α)]= ω0qmsin(ω0t α),
dt dt
sin(ω0t + α) = cos(ω0t α ),
2
i(t) = imcos(ω0t α ),
2
Воспользовавшись формулой приведения
13.
ЭНЕРГИЯ СВОБОДНЫХ ГАРМОНИЧЕСКИХ МЕХАНИЧЕСКИХКОЛЕБАНИЙ.
1 2 2 2
1 2 2
W = kX cos (ω0t + α) = mω X cos (ω0t α ),
p 2 m
2 0 m
1 2
W = m
k 2
= m sin(ω0t α ), m = ω0 X m ,
1 2 2 2
W = mω X sin (ω0t α ),
k 2
0 m
1
W = mω2 X 2 = const
0 m
2





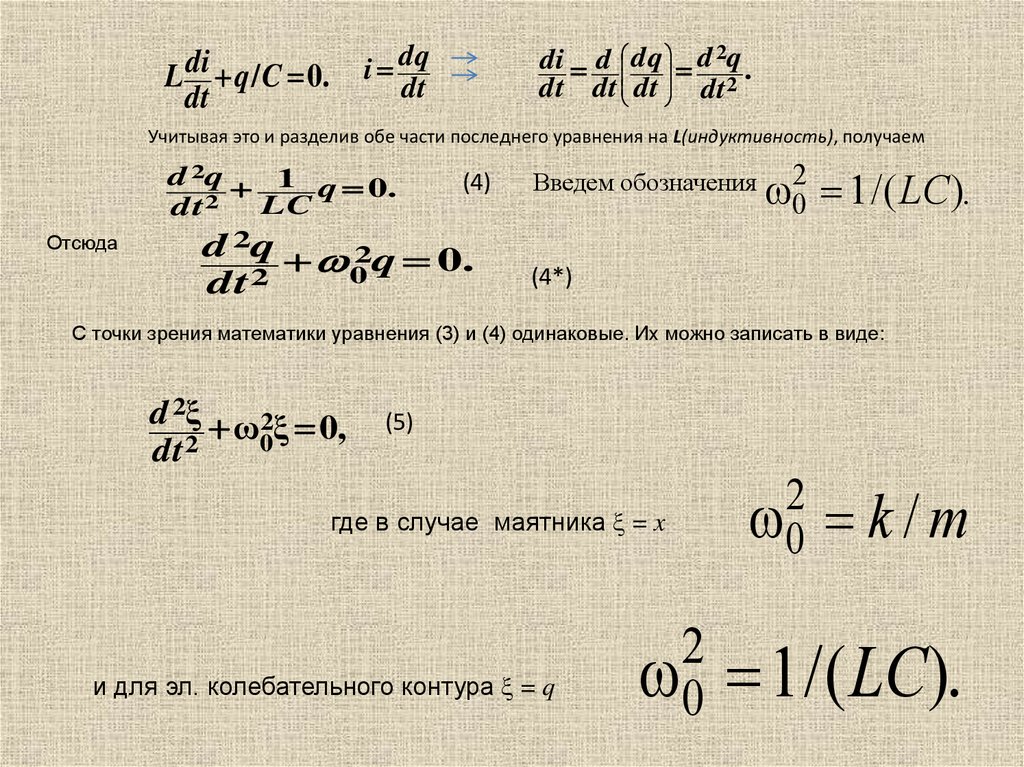






 physics
physics








