Similar presentations:
Динамика твердого тела. Лекция 5: Плоское движение твердого тела
1. ДИНАМИКА ТВЕРДОГО ТЕЛА
ЛЕКЦИЯ 5:ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО
ТЕЛА
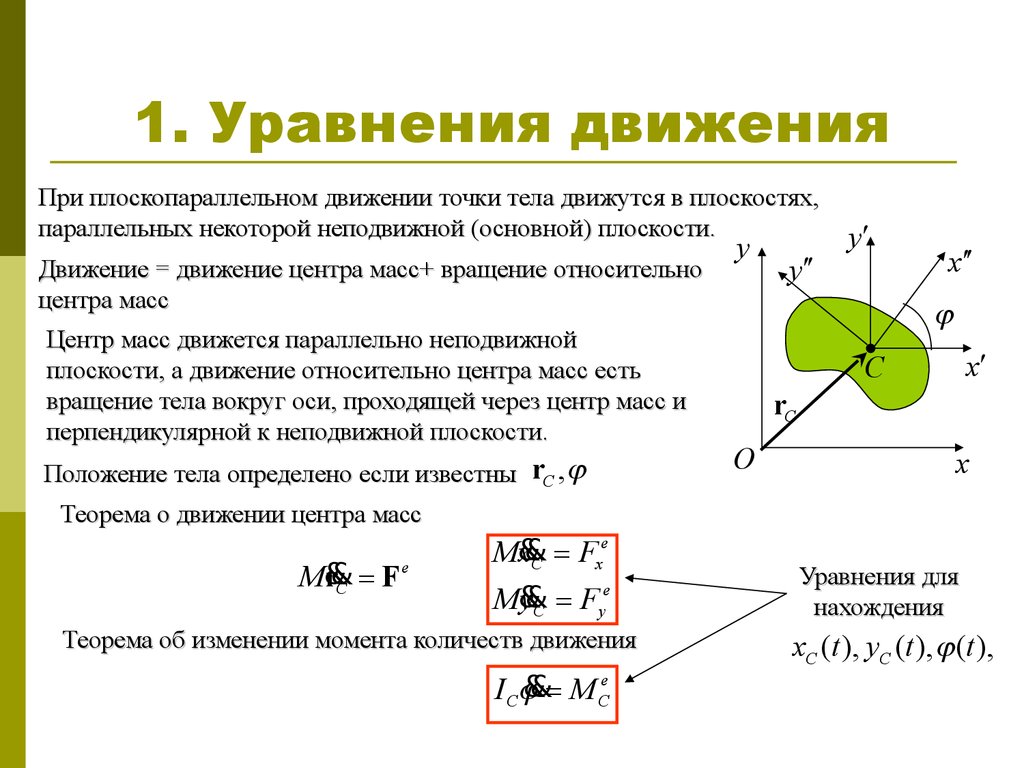
2. 1. Уравнения движения
При плоскопараллельном движении точки тела движутся в плоскостях,параллельных некоторой неподвижной (основной) плоскости.
Движение = движение центра масс+ вращение относительно
центра масс
Центр масс движется параллельно неподвижной
плоскости, а движение относительно центра масс есть
вращение тела вокруг оси, проходящей через центр масс и
перпендикулярной к неподвижной плоскости.
Положение тела определено если известны rC , j
y
y ¢¢
y¢
x¢¢
j
x¢
C
rC
O
x
Теорема о движении центра масс
e
M&
r&
=
F
C
e
&
Mx&
=
F
C
x
&
My&
C = F
e
y
Теорема об изменении момента количеств движения
&= M Ce
I Cj&
Уравнения для
нахождения
xC (t ), yC (t ), j (t ),
3. 2. Использование теоремы об изменении кинетической энергии
При интегрировании системы уравнений движения можно эти уравнения заменятьдругими, получающимися в результате их взаимных комбинаций.
В частности, иногда удобно использовать теорему об изменении кинетической энергии
По теореме Кенига кинетическая энергия равна
M 2
IC 2
2
T=
x&C + y&C ) + j&
(
2
2
По теореме об изменении кинетической энергии
T - T0 = Ae
Изменение кинетической энергии = Работа внешних сил
4. 3. Использование теоремы моментов для оси z неподвижной системы
Кинетический момент относительно неподвижного центра О равен суммекинетического момента центра масс, в котором сосредоточена масса тела,
относительно центра О и кинетического момента тела относительно центра С в его
движении по отношению к системе осей, проходящих через центр масс и
перемещающихся поступательно
KOz
dr ö
æ
K O = ç rC ´ M C ÷ + K ¢C
dt ø
è
dx ö
dj
æ dy
= M ç xC C - yC C ÷ + I C
dt
dt ø
dt
è
d é æ dyC
dxC ö
dj ù
e
e
M
x
y
+
I
=
x
F
y
F
(
å
C
i iy
i ix )
ç C
÷ C
ê
ú
dt ë è
dt
dt ø
dt û 1 4 4 2 4 4 3
Me
Oz
5. 4. Пример 1: скольжение цилиндра по наклонной плоскости
Тяжелый круглый цилиндр движется, касаясьабсолютно гладкой наклонной плоскости, так, что
ось цилиндра остается все время горизонтальной.
Движение происходит параллельно вертикальной
плоскости, перпендикулярной к оси цилиндра.
Найти уравнения движения цилиндра.
Уравнения
движения
Уравнения связи
&
ì Mx&
C = Mg sin a
ï
&
í My&
C = - Mg cos a + N
ï
&= 0
I Cj&
î
yC = R Þ
&
y&
Þ N = Mg cos a
C =0
Цилиндр вращается с постоянной угловой скростью j&= w = const , сообщенной
x&
ему в начальный момент и движется с постоянным ускорением &
C = g sin a
6. 5. Пример 2: качение цилиндра без проскальзывания
Тяжелый круглый цилиндр катится пошероховатой наклонной плоскости без
скольжения. Исследовать движение цилиндра.
Уравнения
движения
&
ì Mx&
C = Mg sin a - F
ï
&
í My&
C = - Mg cos a + N
ï
&= FR
I Cj&
î
Уравнения связи 1
Уравнения связи 2
g sin a
I
1+ C 2
MR
IC &
x&
F = 2C
R
A
yC = R Þ &
y&
Þ N = Mg cos a
C =0
&
&
v A = 0, v A = vC - Rj& Þ x&C = Rj& Þ &
x&
C = Rj
&
x&
C =
Когда возможно такое движение?
2
g sin a
3
1
F = Mg sin a
3
Для однородного
цилиндра
&
x&
C =
MR 2
IC =
2
F £ fN
Û
1
f ³ tg a
3
7. 6. Пример 3: качение цилиндра с проскальзыванием
Тяжелый круглый цилиндр катится по1
шероховатой наклонной плоскости.
f < tg a
3
Исследовать движение цилиндра.
Уравнения
движения
&
ì Mx&
C = Mg sin a - F
ï
&
í My&
C = - Mg cos a + N
ï
&= FR
I Cj&
î
A
yC = R Þ &
y&
Þ N = Mg cos a
C =0
&
F = fN Þ Mx&
C = Mg (sin a - f cos a )
MR 2
&= fMgR cos a
j&
&
x&
=
g
(sin
a
f
cos
a
)
C
2
&= 2 fgR -1 cos a
j&
Уравнения связи 1
Уравнения связи 2
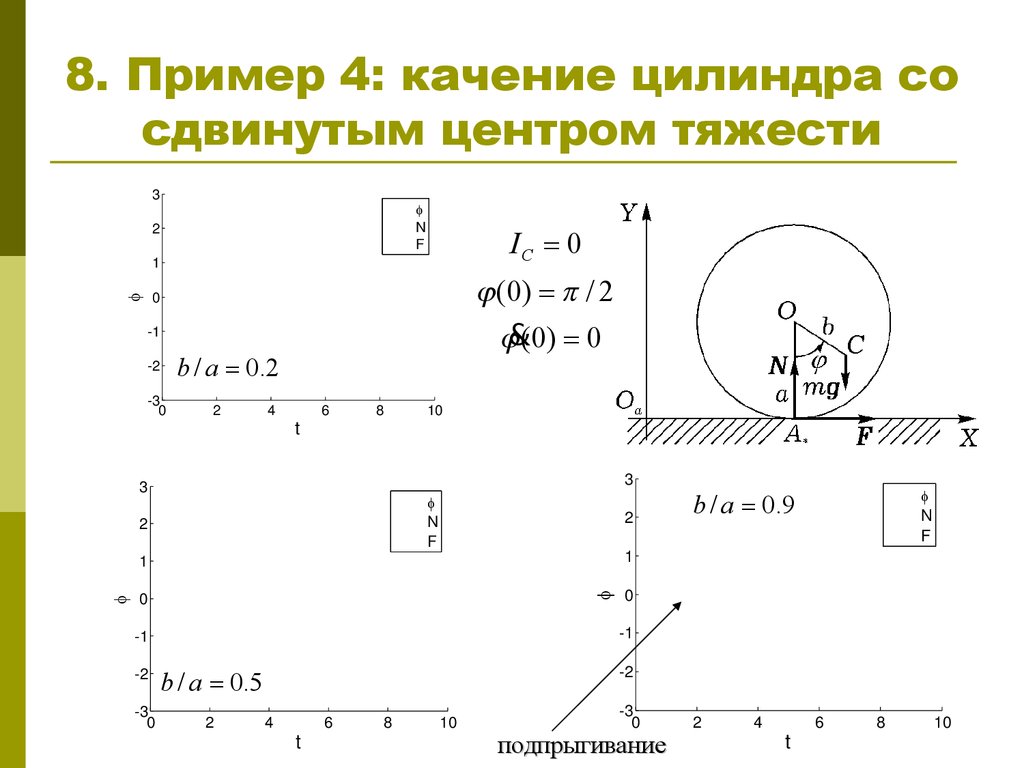
8. 7. Пример 4: качение цилиндра со сдвинутым центром тяжести
Неоднородный диск катится без скольжения понеподвижной горизонтальной плоскости. Масса
диска равна m, радиус a, центр масс С находится
на расстоянии b от геометрического центра,
момент инерции относительно оси,
перпендикулярной плоскости диска и проходящей
через его центр масс, равен Ic . Получить
дифференциальные уравнения движения диска.
&
mx&
ì
C = F
Уравнения ï
&
my&
C = N - mg
движения í
ï I j&
î C &= F ( a - b cos j ) - Nb sin j
vA = 0
vO = - aj&
&+ cos jj&2 )
N = mg + mb ( sin jj&
x&C = vO + b cos jj&= - ( a - b cos j ) j&
y&C = b sin jj&
&+ b sin jj&2 )
F = -m ( ( a - b cos j ) j&
Þ
é I C + m ( a 2 + b2 - 2ab cos j ) ù j&
&+ mab sin jj&2 + mgb sin j = 0
ë
û
9. 8. Пример 4: качение цилиндра со сдвинутым центром тяжести
3N
F
2
IC = 0
1
j (0) = p / 2
j&(0) = 0
0
1
b / a = 0.2
2
3
0
2
4
t
6
8
3
3
N
F
2
2
1
1
0
0
10
N
F
b / a = 0.9
1
1
2
b / a = 0.5
3
0
2
2
4
t
6
8
10
3
0
подпрыгивание
2
4
t
6
8
10
10. 9. Пример 5: падение стержня
Однородный стержень массы m и длины 2lрасположен вертикально. Нижний конец опирается на
гладкую плоскость. После того как ему задали
бесконечно малое смещение от вертикали он начал
падать. Получить ДУ движения.
l
N
1) Горизонтальных сил нет. Центр масс падает вертикально
2) Закон сохранения энергии
1 2 1 æ 1 2 ö &2
my& + ç ml ÷ q + mgy = const
2
2è3
ø
y = l cos q , y&= -l sin qq&
3) Уравнение связи
( 3sin 2 q + 1) lq&2 + 6 g cosq = const=6g
l
mg
q y
x
6 g ( 1 - cos q )
q&2 =
l ( 3sin 2 q + 1)
11. 10. Пример 5: падение стержня
6 gl sin 2 q ( 1 - cos q )y& =
3sin 2 q + 1
l
2
6 gl cos 2 q ( 1 - cos q )
2
x& =
3sin 2 q + 1
N
Горизонтальная скорость имеет максимум
6 glc ( 1 - c )
c = cos q
x& =
2
4 - 3c
dx&2
= 0 Þ 3c 3 - 12c + 8 = 0 Þ q = 37o50¢
dc
l
mg
q y
x
2
x&max = 0.61 gl
12. 11. Пример 6: падение стержня
Тонкий однородный стержень приставлен одним концом кгладкой вертикальной стене, а другим концом опирается на
гладкий пол. Стержень пришел в движение из состояния
покоя, когда он составлял угол a с вертикалью. Вычислить
начальные давления на стену и пол.
&= N A
mx&
&= N B - mg
my&
ma 2
1
1
&
&
j = - N Aa cos j + N B a sin j
12
2
2
x=
1
1
a sin j , y = a cos j
2
2
a
&- sin jj&2 )
cos jj&
(
2a
Þ
&+ cos jj&2 )
&
y&= - ( sin jj&
2
&
x&=
13. 12. Пример 6: падение стержня
ma&- sin jj&2 )
cos jj&
(
2
ma
&+ cos jj&2 )
N B = mg sin jj&
(
2
2
ma
1
1
&= - N Aa cos j + N B a sin j
j&
12
2
2
NA =
&(0) =
j (0) = a , j&(0) = 0, j&
3mg
N A (0) =
sin 2a
8
&=
j&
3g
sin j
2a
3g
sin a
2a
æ 3
ö
N B (0) = mg ç 1 - sin 2 a ÷
è 4
ø











 physics
physics








