Similar presentations:
Площадь треугольника
1. Площадь треугольника
2.
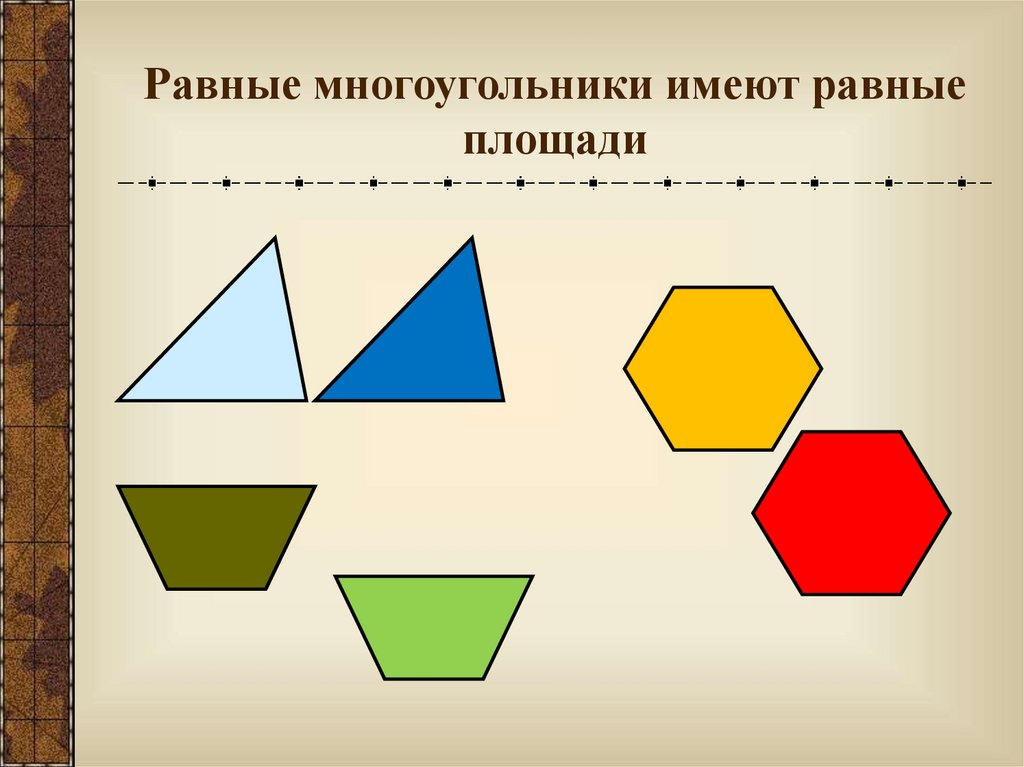
Равные многоугольники имеют равныеплощади
3.
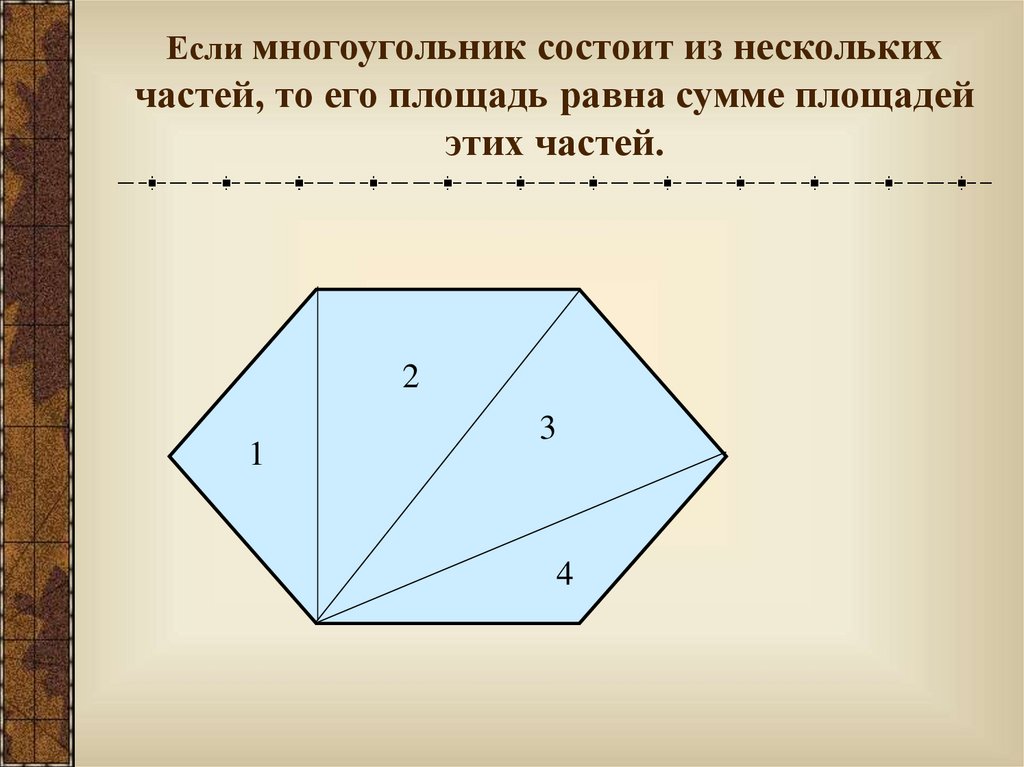
Если многоугольник состоит из несколькихчастей, то его площадь равна сумме площадей
этих частей.
2
1
3
4
4.
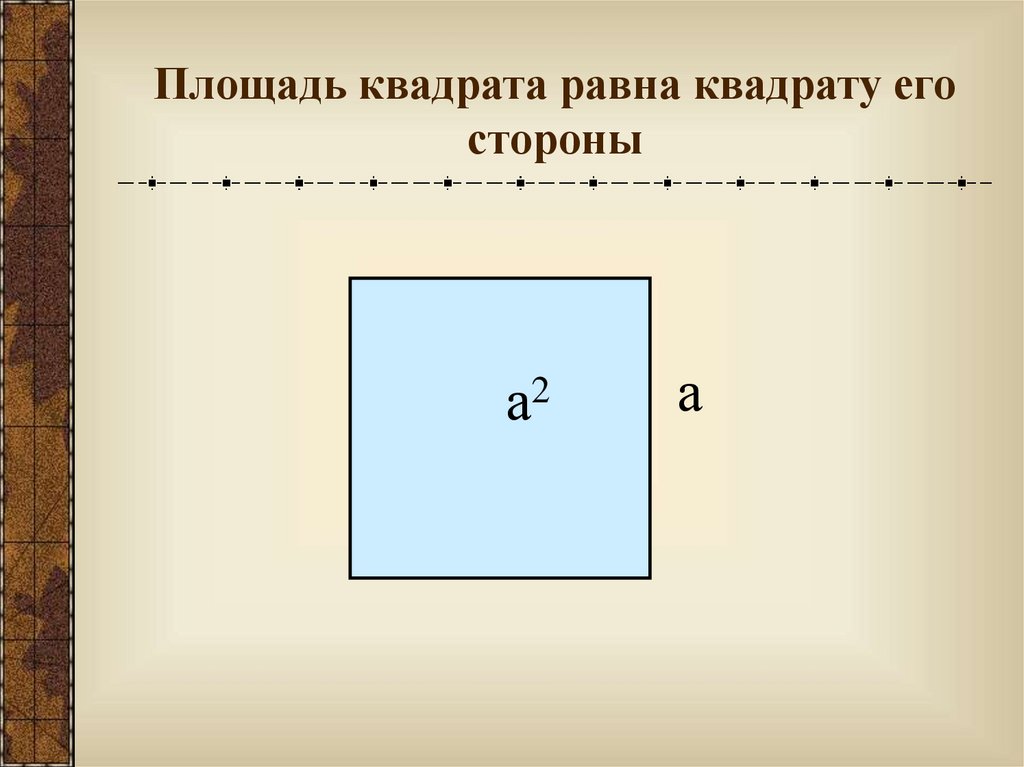
Площадь квадрата равна квадрату егостороны
а2
а
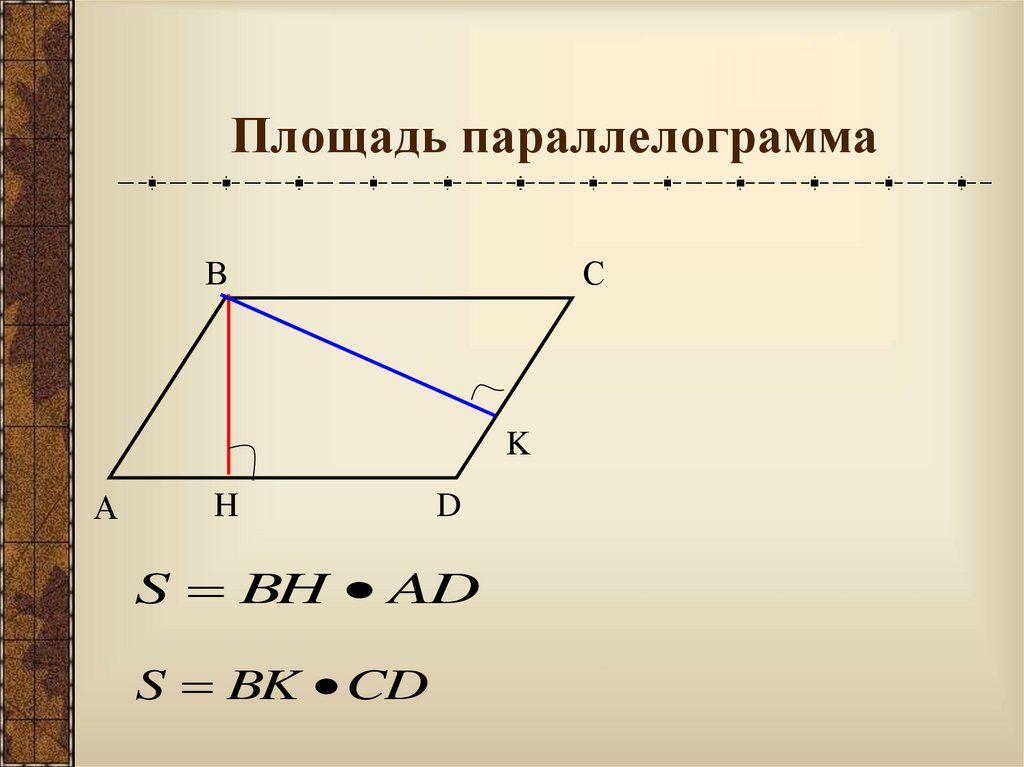
5. Площадь параллелограмма
ВС
K
А
H
D
S BH AD
S BK CD
6.
Задача 460B
C
Дано:
ABCD-параллелограмм,
BD=13см,
D
A
BD AD,
AD=12см.
Найти : S пар-ма
Решение:
BD AD, BD высота
\ АD BD 12 13 156см 2
7.
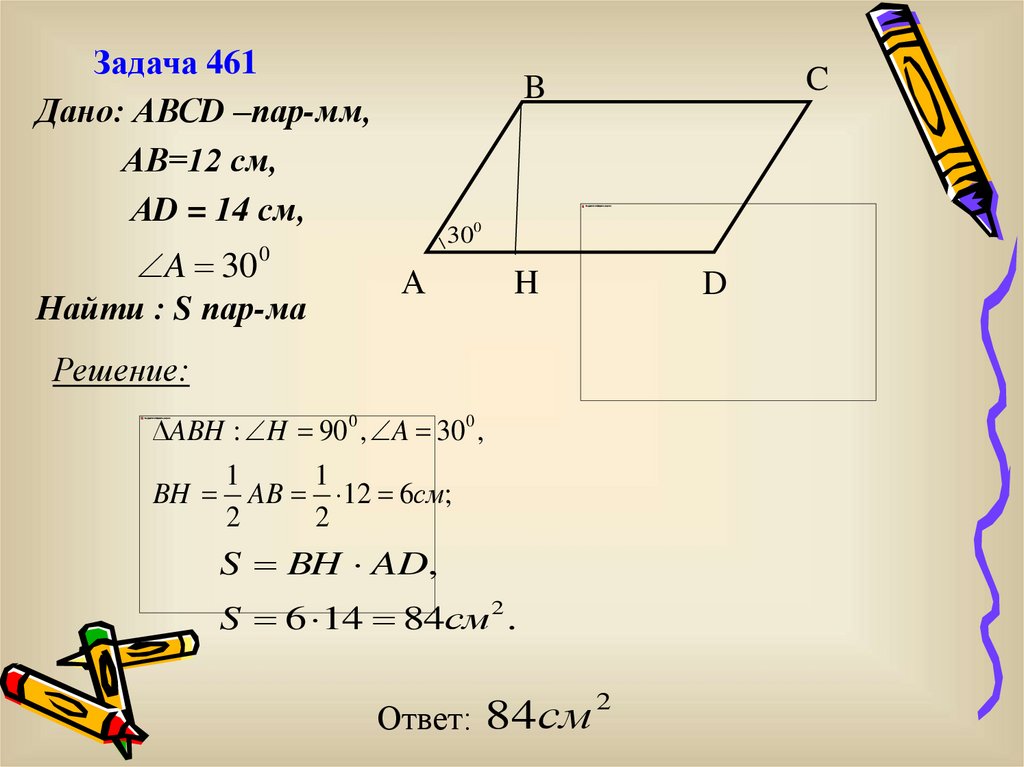
Задача 461Дано: АВСD –пар-мм,
АВ=12 см,
АD = 14 см,
A 300
Найти : S пар-ма
300
А
H
Решение:
ABH : H 90 0 , A 30 0 ,
BH
C
B
1
1
AB 12 6см;
2
2
S BH AD,
S 6 14 84см 2 .
2
84см
Ответ:
D
8.
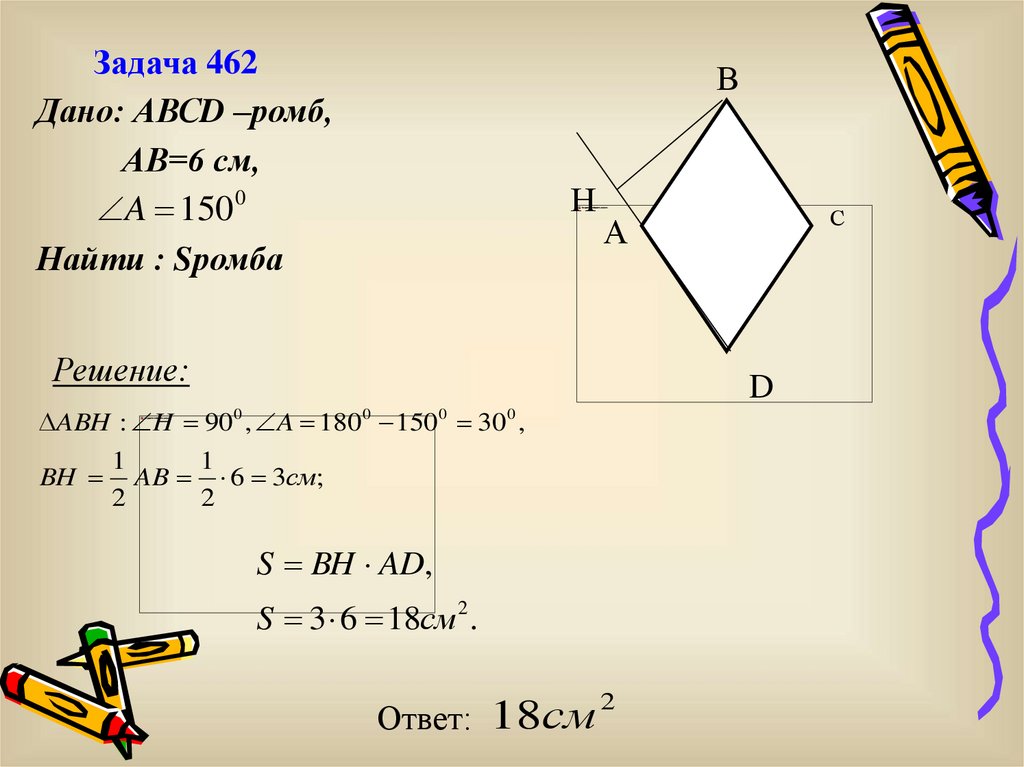
Задача 462Дано: АВСD –ромб,
АВ=6 см,
A 150 0
Найти : Sромба
В
Н
А
Решение:
ABH : H 90 0 , A 180 0 150 0 30 0 ,
BH
С
1
1
AB 6 3см;
2
2
S BH AD,
S 3 6 18см 2 .
2
18см
Ответ:
D
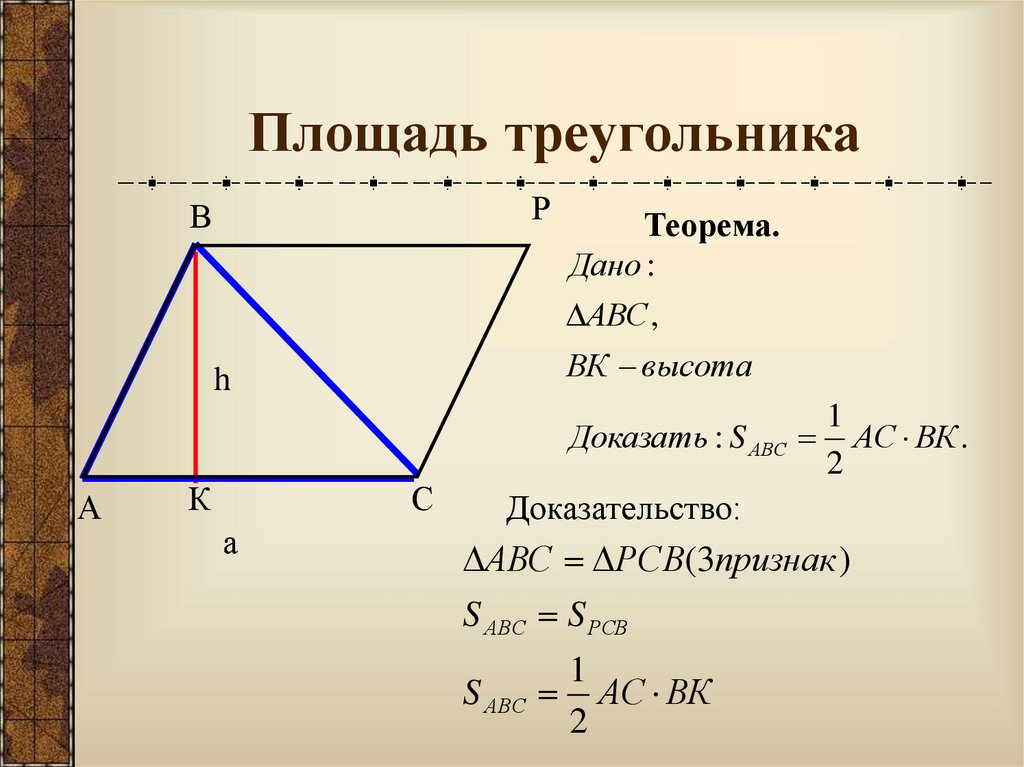
9. Площадь треугольника
РВ
h
Теорема.
Дано :
АВС ,
ВК высота
Доказать : S АВС
А
К
С
а
1
АС ВК .
2
Доказательство:
АВС РСВ(3признак )
S АВС S РСВ
S АВС
1
АС ВК
2
10.
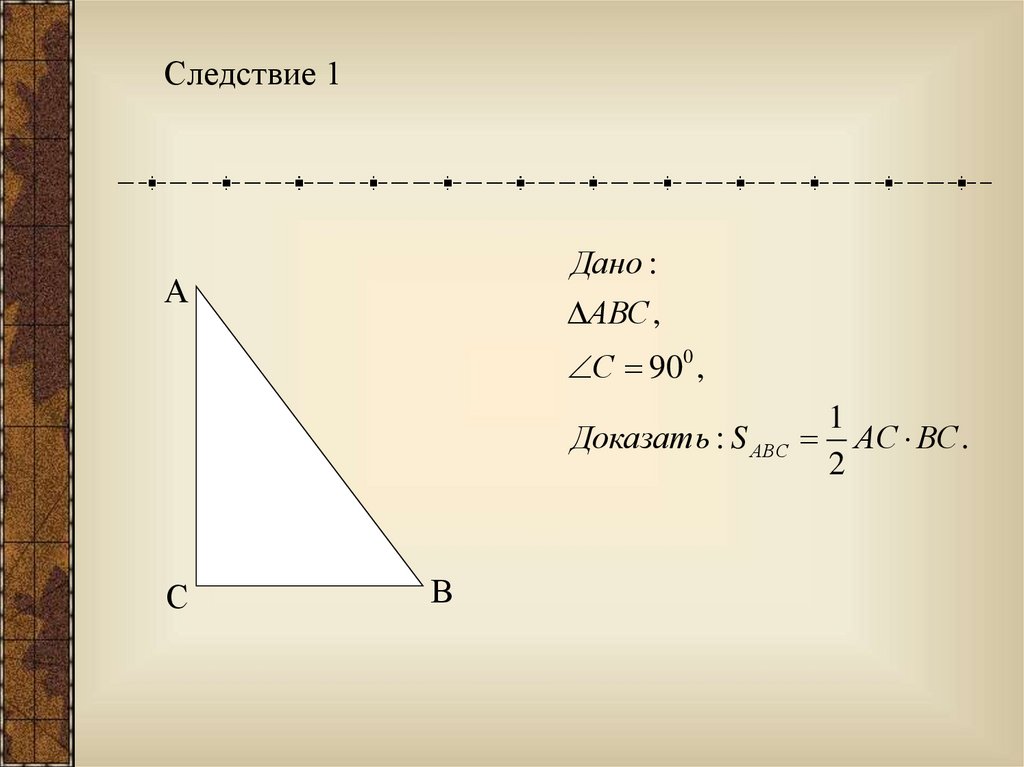
Следствие 1Дано :
А
АВС ,
С 90 0 ,
Доказать : S АВС
С
В
1
АС ВС .
2
11.
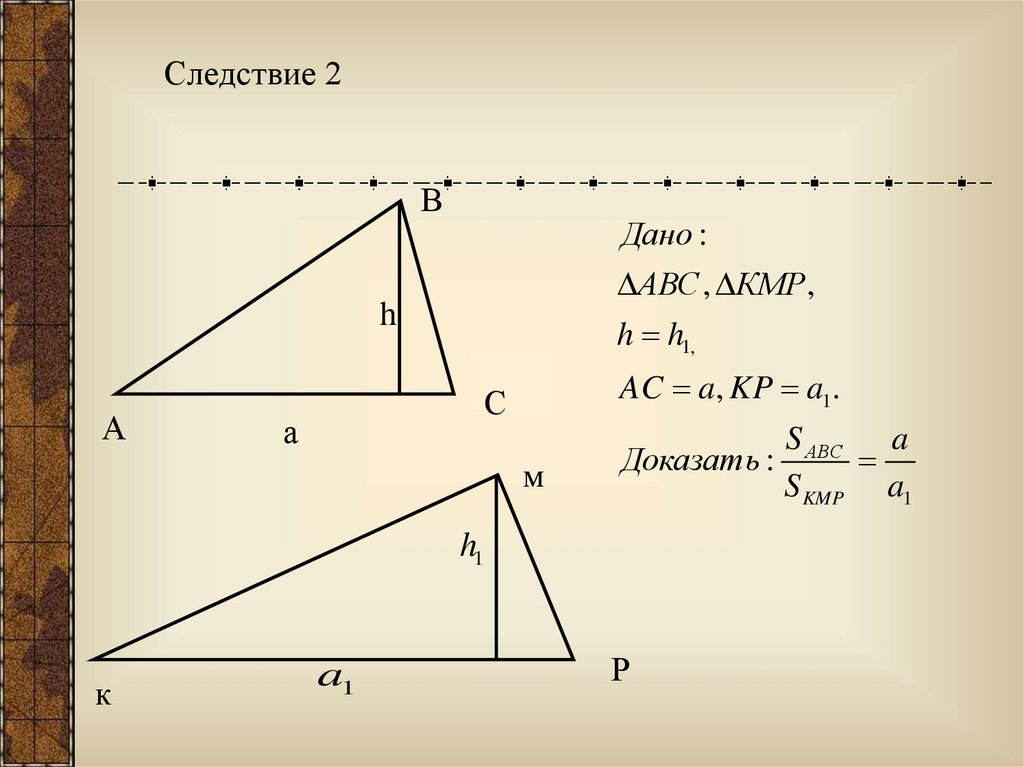
Следствие 2В
Дано :
АВС , КМР,
h
А
h h1,
AC a, KP a1.
С
а
м
Доказать :
h1
к
a1
Р
S АВС a
S KMP a1
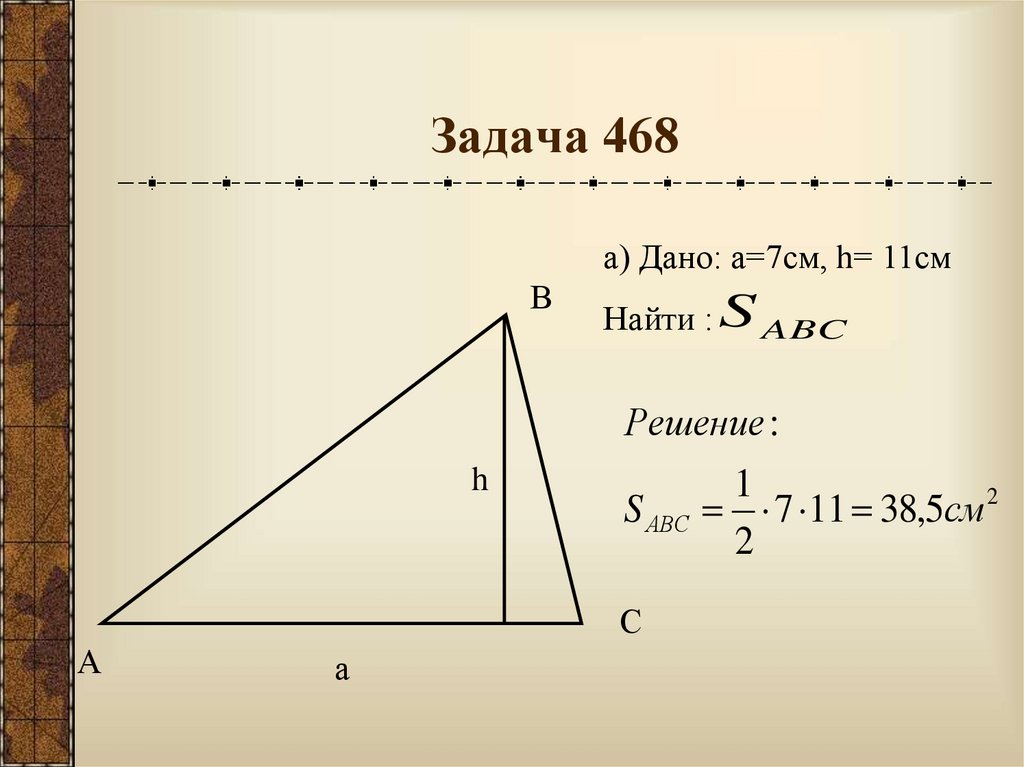
12. Задача 468
а) Дано: а=7см, h= 11смВ
Найти : S ABC
Решение :
h
S АВС
С
А
а
1
7 11 38,5см 2
2
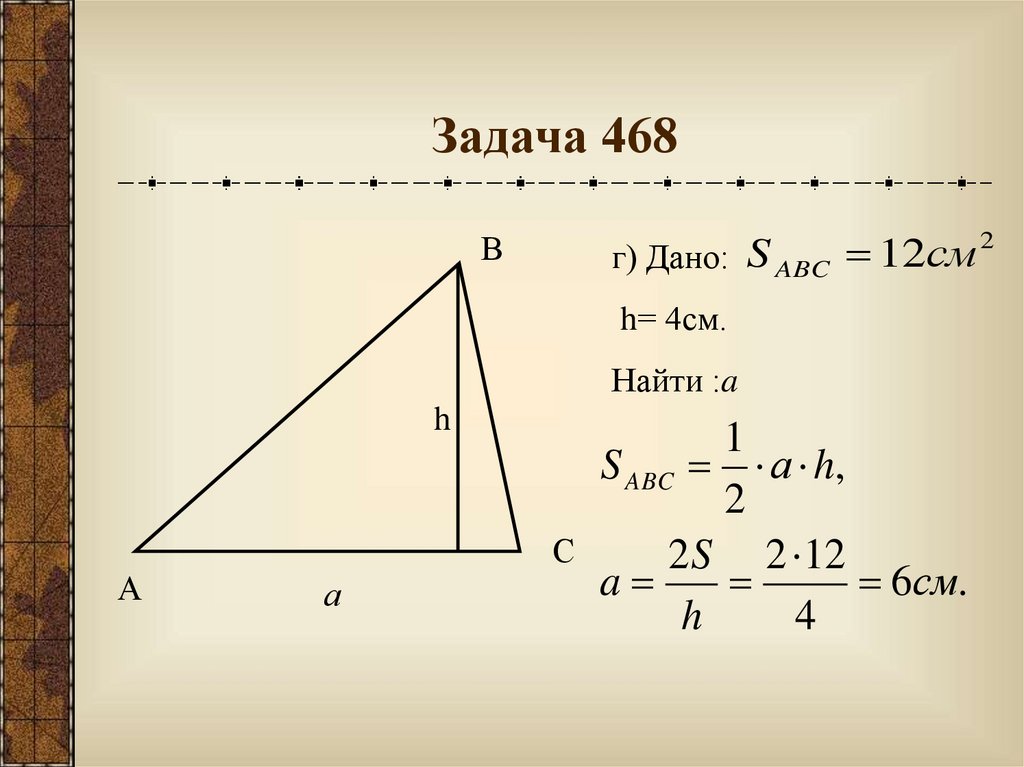
13.
Задача 468В
г) Дано:
S ABC 12см
h= 4см.
Найти :a
h
А
С
а
1
S ABC а h,
2
2 S 2 12
a
6см.
h
4
2
14.
471(а), 475.Домашнее задание:
п.53,
задачи 467,468(б,в),471(б).
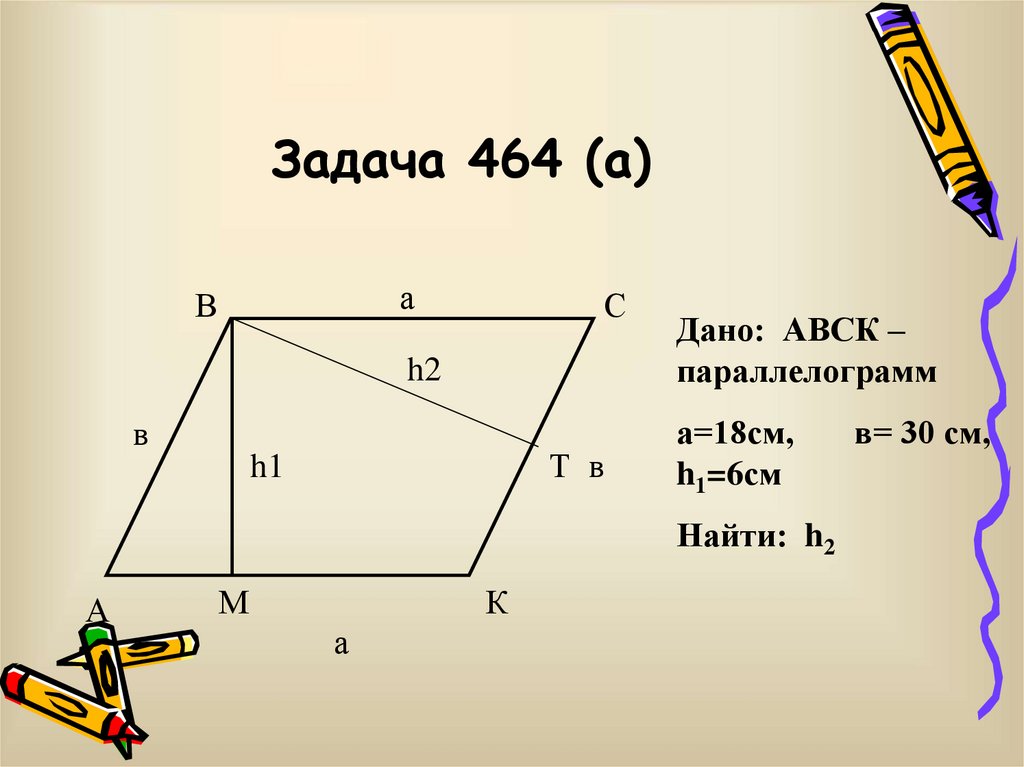
15. Задача 464 (a)
аВ
С
h2
в
Т в
h1
Дано: АВСК –
параллелограмм
а=18см,
h1=6см
Найти: h2
А
М
К
а
в= 30 см,
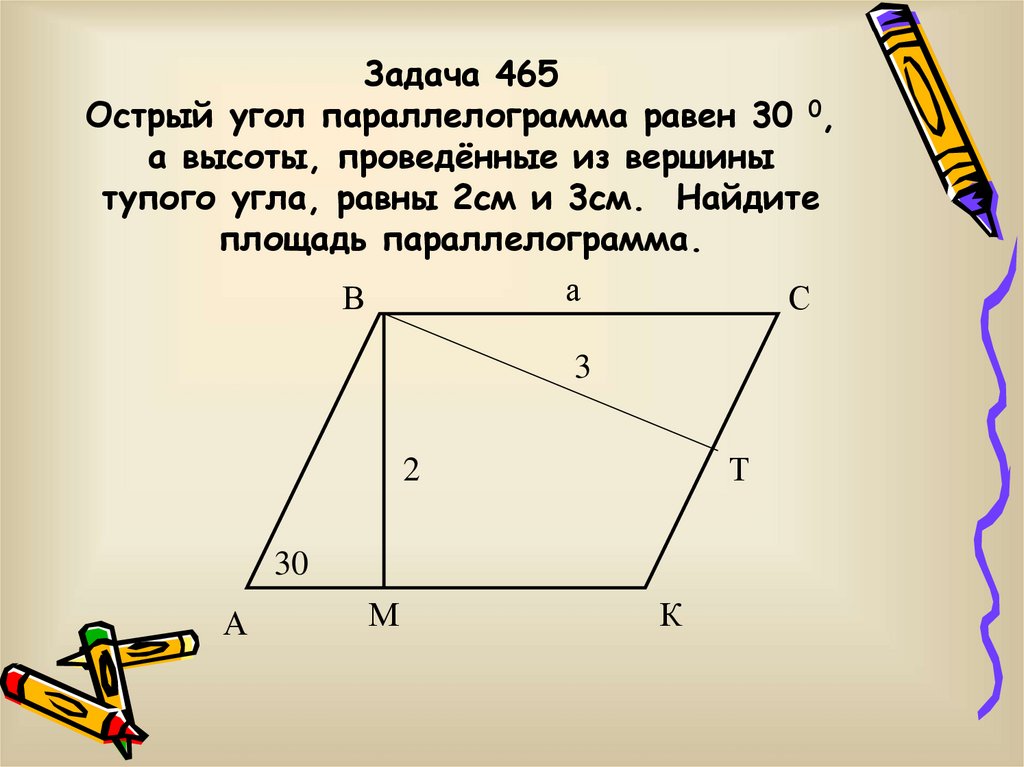
16. Задача 465 Острый угол параллелограмма равен 30 0, а высоты, проведённые из вершины тупого угла, равны 2см и 3см. Найдите
площадь параллелограмма.а
В
С
3
Т
2
30
А
М
К
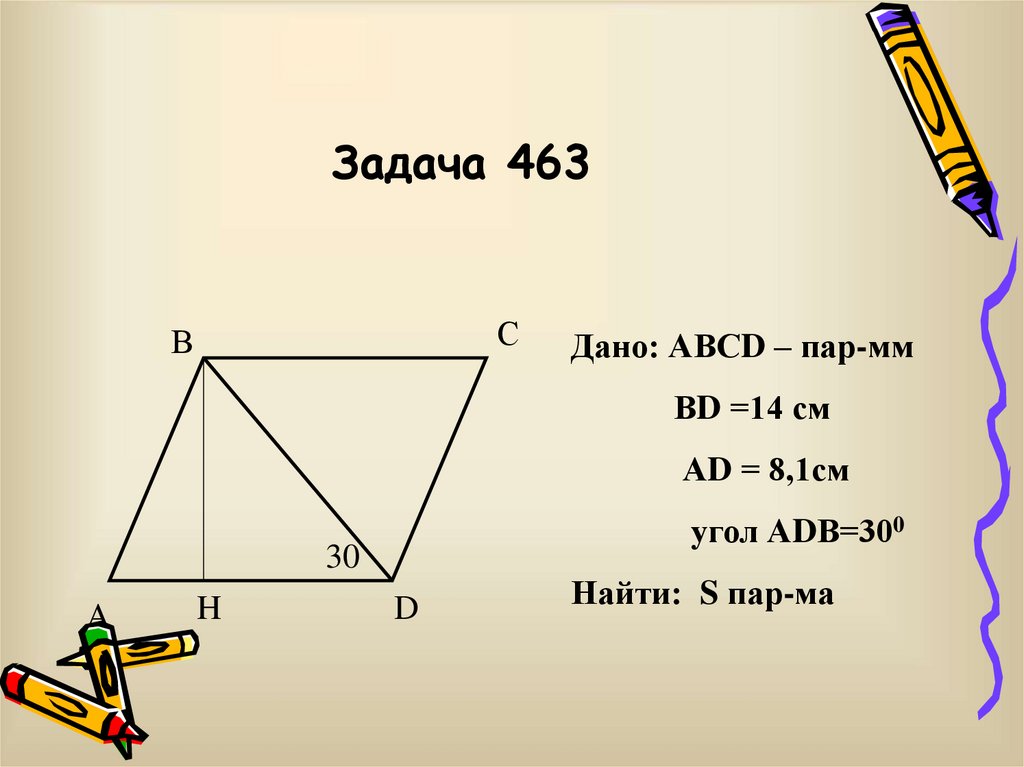
17. Задача 463
СВ
Дано: АВСD – пар-мм
ВD =14 см
АD = 8,1см
угол АDВ=300
30
А
H
D
Найти: S пар-ма


 mathematics
mathematics








