Свойство медианы равнобедренного треугольника

1. Тема урока:

27.01.2009
Тема урока:
«Свойство медианы
равнобедренного треугольника».

2.

3. Определение равнобедренного треугольника

основание

4. Свойство равнобедренного треугольника

1= 2
1
2

5. Определение равностороннего треугольника

6. Первый признак равенства треугольников

=

7. Второй признак равенства треугольников

=

8. Сформулируйте определения!

Биссектриса треугольника – это…
Медиана треугольника – это…
Высота треугольника – это…

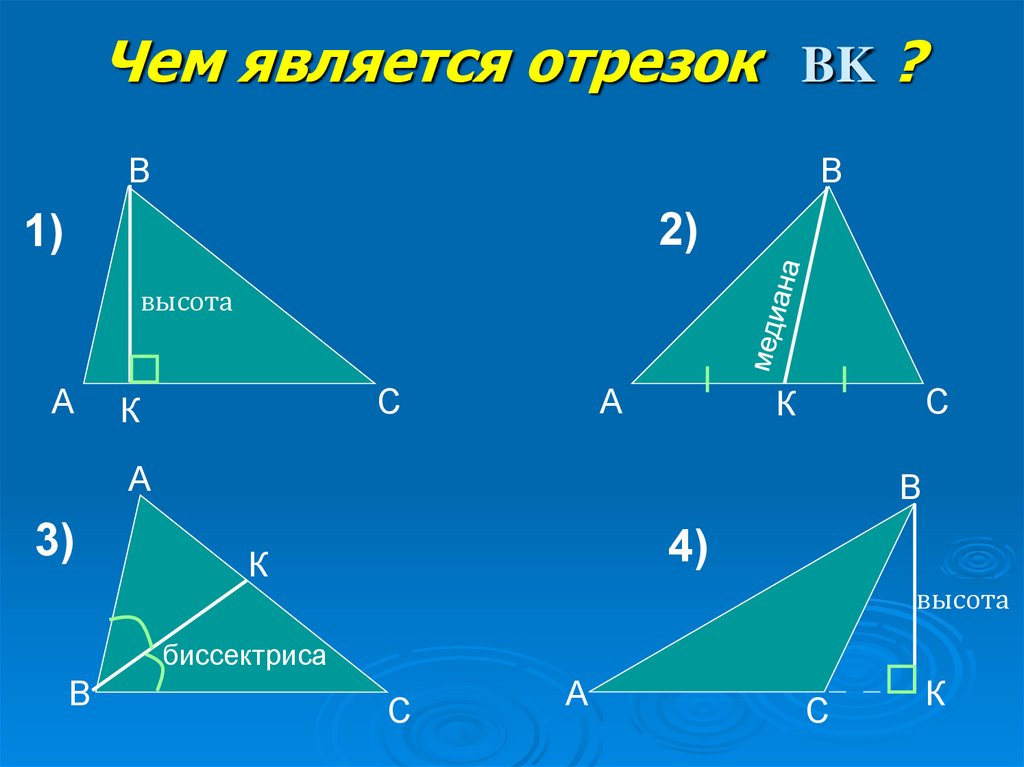
9. Чем является отрезок BK ?

В
В
2)
1)
высота
А
С
К
А
С
К
А
3)
В
4)
К
высота
биссектриса
В
С
А
С
К

10. Решаем устно!

P
Дано: OPK – равносторонний;
OM – медиана; OK = 5 см.
M
MK - ?
?
O
5
K
2,5 см
MK = 2,5

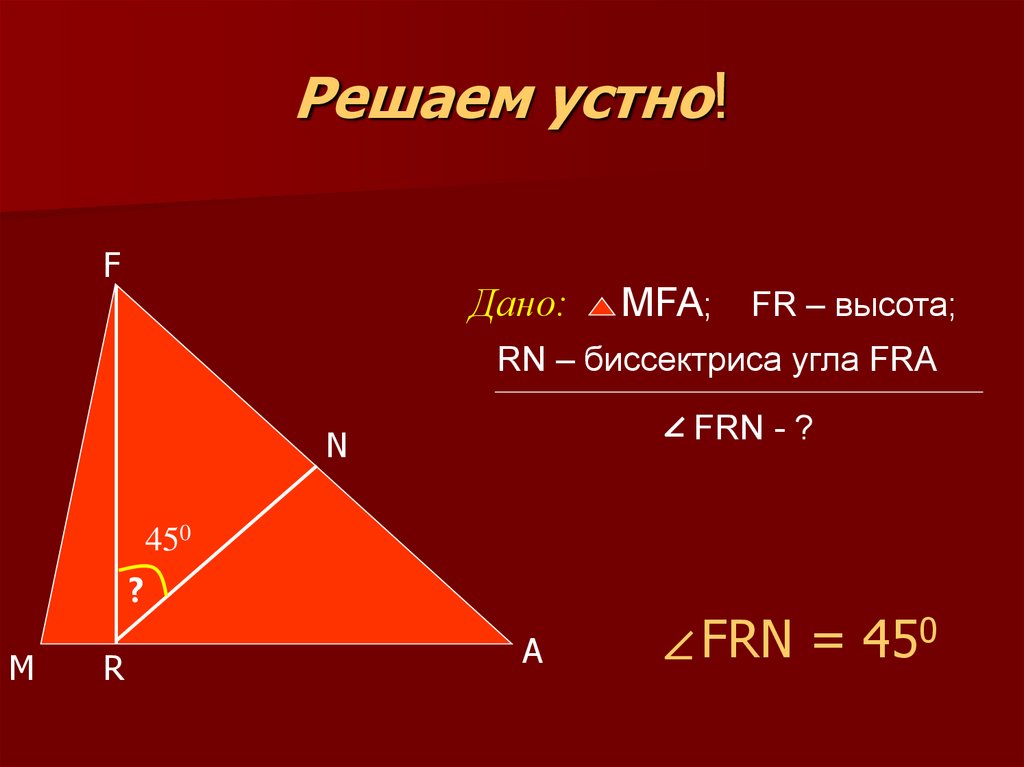
11. Решаем устно!

F
Дано:
MFA; FR – высота;
RN – биссектриса угла FRA
FRN - ?
N
450
?
M
R
A
FRN = 450

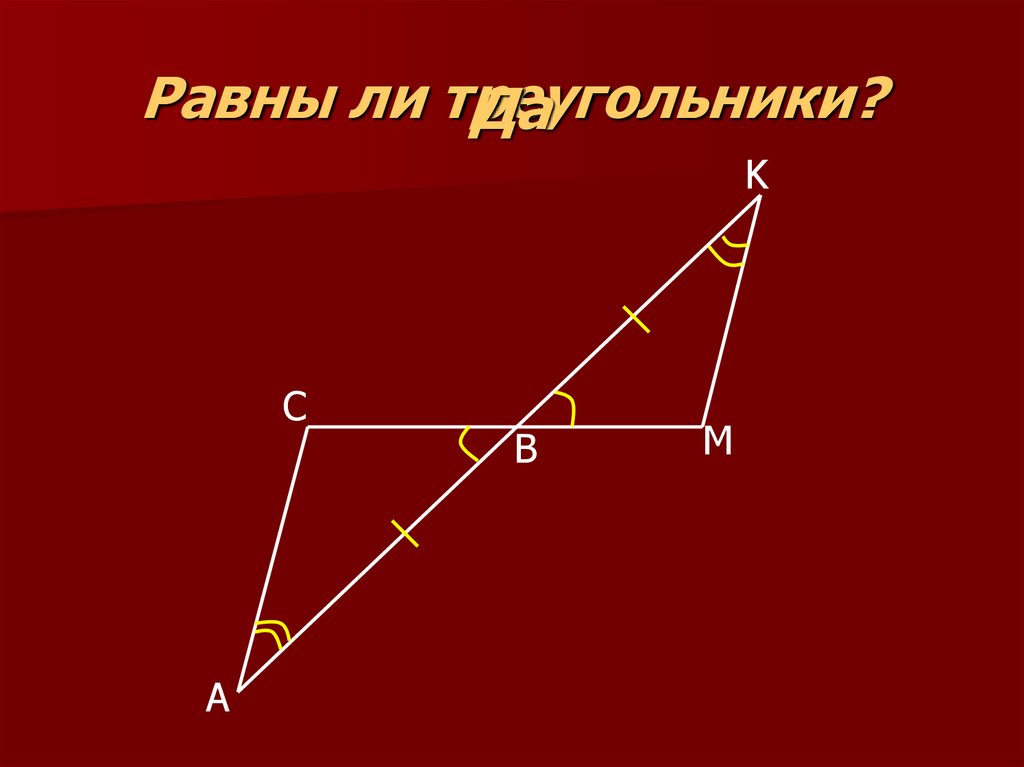
12. Равны ли треугольники?

=

13. Равны ли треугольники?

=

14. Равны ли треугольники?

Да
K
C
A
B
M

15. Изучение нового материала

«Свойство медианы
равнобедренного треугольника»

16. Теорема.

B
Дано: ABC – равнобедренный;
Медиана равнобедренного
треугольника,
BD - медиана
проведённая кBD
основанию,
является
– биссектриса; BD - высота
биссектрисой и высотой.
Доказательство:
A
D
C
1) AB = BC (по определению равноб.треугольника)
2) AD = DC (по определению медианы)
3) A = C (по свойству равноб. треугольника) =
ABD = CBD (по 1 признаку) =
ABD = CBD (т.е.
BD - биссектриса) и смежные углы ADB и CDB тоже
равны = углы ADB и CDB – прямые (т.е. BD - высота).

17.

№ 25(1)

18.

Сформулируйте свойство медианы
равнобедренного треугольника.
Медиана равнобедренного
треугольника,
проведённая к основанию, является
биссектрисой и высотой.

19.

• переписать доказательство и
теорему в тетрадь, выучить их;
• изучить п. 26;
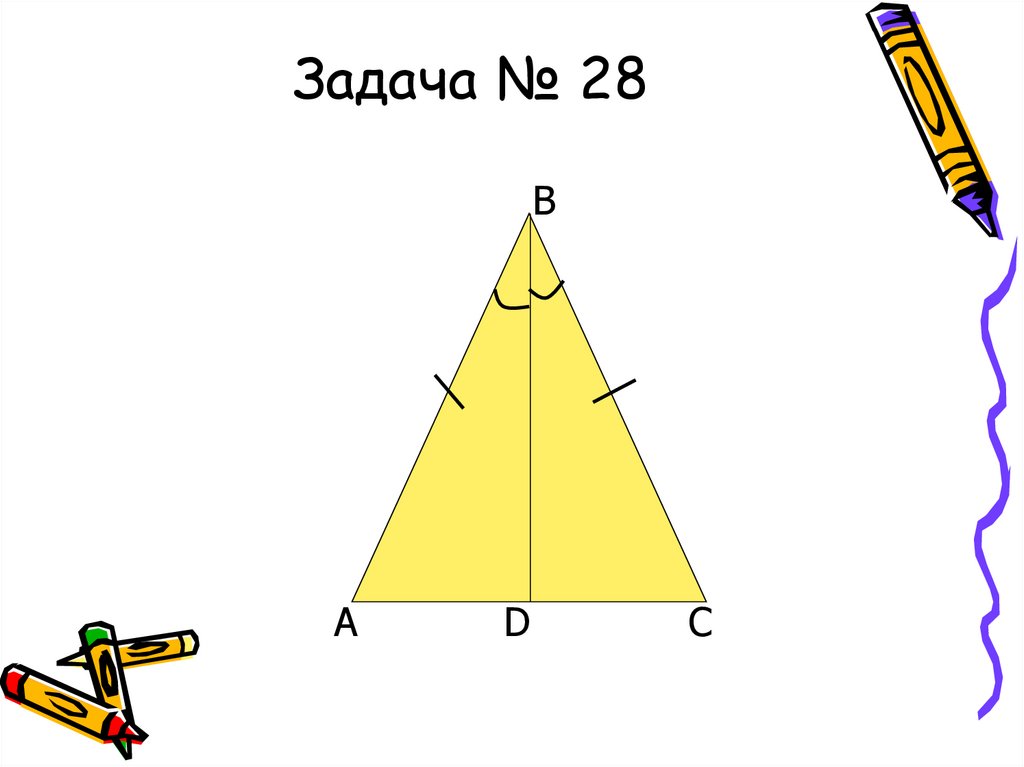
• задача № 28

20. Задача № 28

B
A
D
C

21.

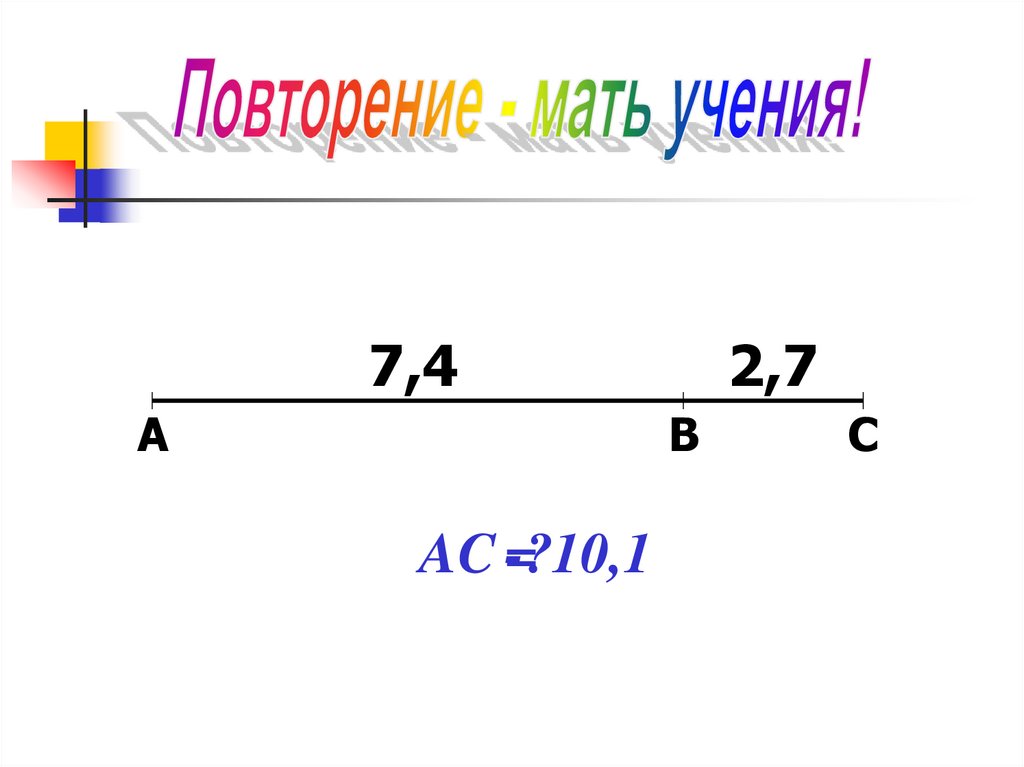
7,4
A
2,7
B
AC -?
= 10,1
C

22.

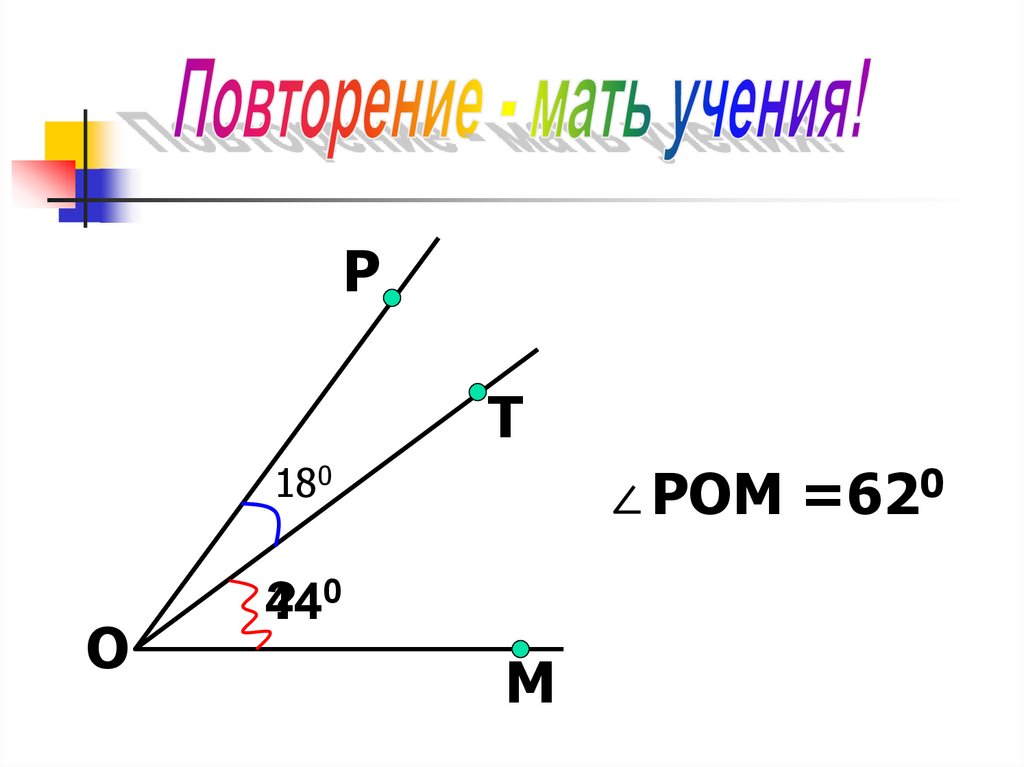
P
T
180
O
POM =620
44 0
?
M

23.

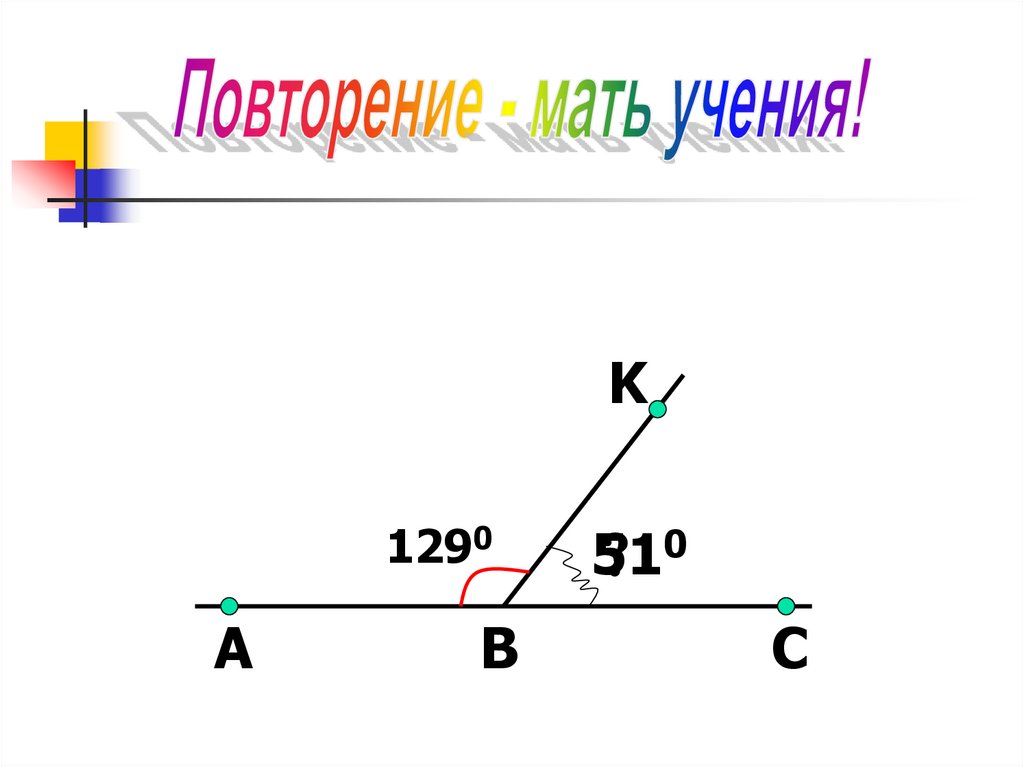
K
1290
A
B
0
51
?
C

24.

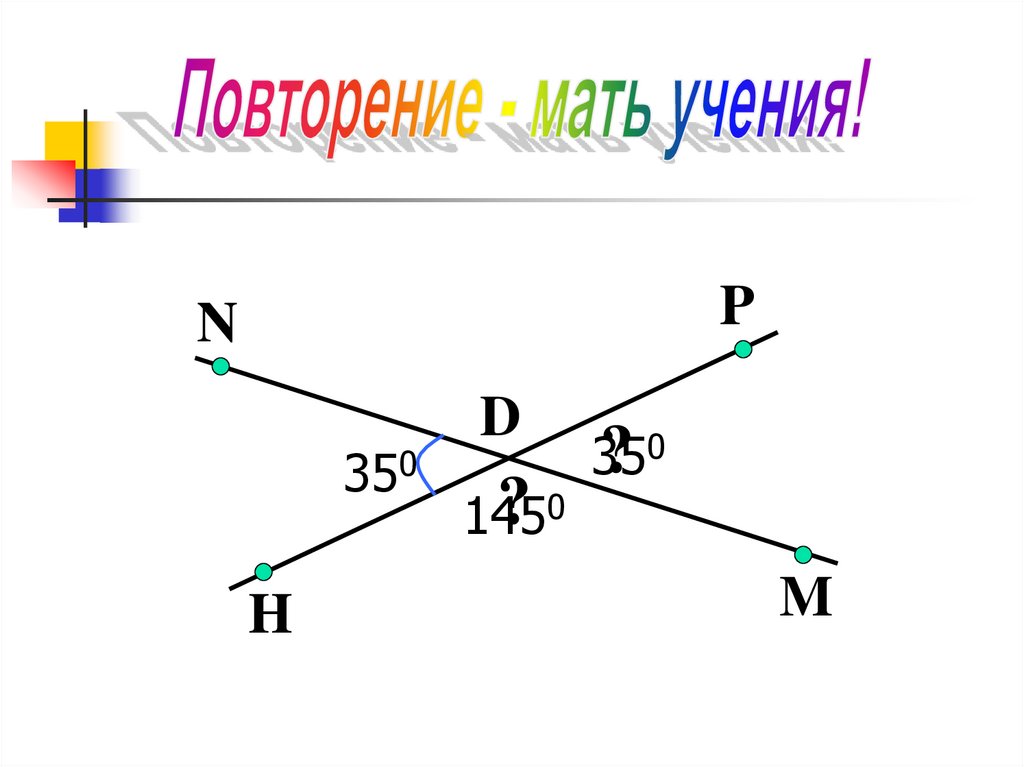
P
N
350
H
D
?0
145
?0
35
M