Равнобедренный треугольник и его свойства

1.

Методическая разработка Кувшиновой О.И. учителя математики
МОУ «СОШ р.п. Духовницкое Духовницкого района Саратовской области»

2. 105. Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и СD к прямой а равны. а) Докажите, что ∆АВD=∆СDВ;

Проверяем домашнее задание.
105.
Точки А и С лежат по одну сторону от прямой а.
Перпендикуляры АВ и СD к прямой а равны. а) Докажите, что
∆АВD=∆СDВ; б)найдите ∟АВС, если ∟АDВ=44°.
А
Дано: АВ ┴ а, СD ┴ а,
С
АВ=СD,
∟АDВ=44°
Доказать: ∆ АВD=∆СDВ;
а
В
D
Найти: ∟АВС
Доказательство:
1. АВ=СD по условию.
2. ∟АВD=∟СВD=90°, т.к. АВ ┴ а, СD ┴ а.
3. ВD – общая.
Следовательно, ∆ АВD=∆СDВ по I признаку
∟АDВ=∟СDВ=44°, ∟АВС=∟АВD -∟СВD= 90°-44°=46°
Ответ: 46°

3.

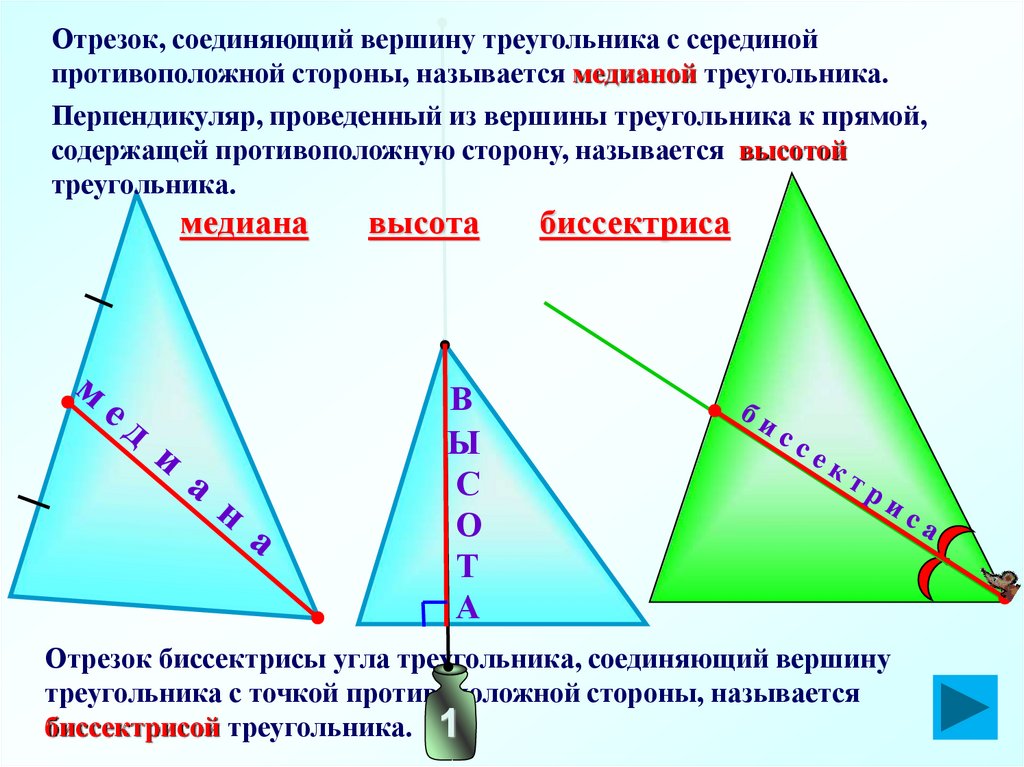
Отрезок, соединяющий вершину треугольника с серединой
противоположной стороны, называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
биссектрисой треугольника. 1

4.

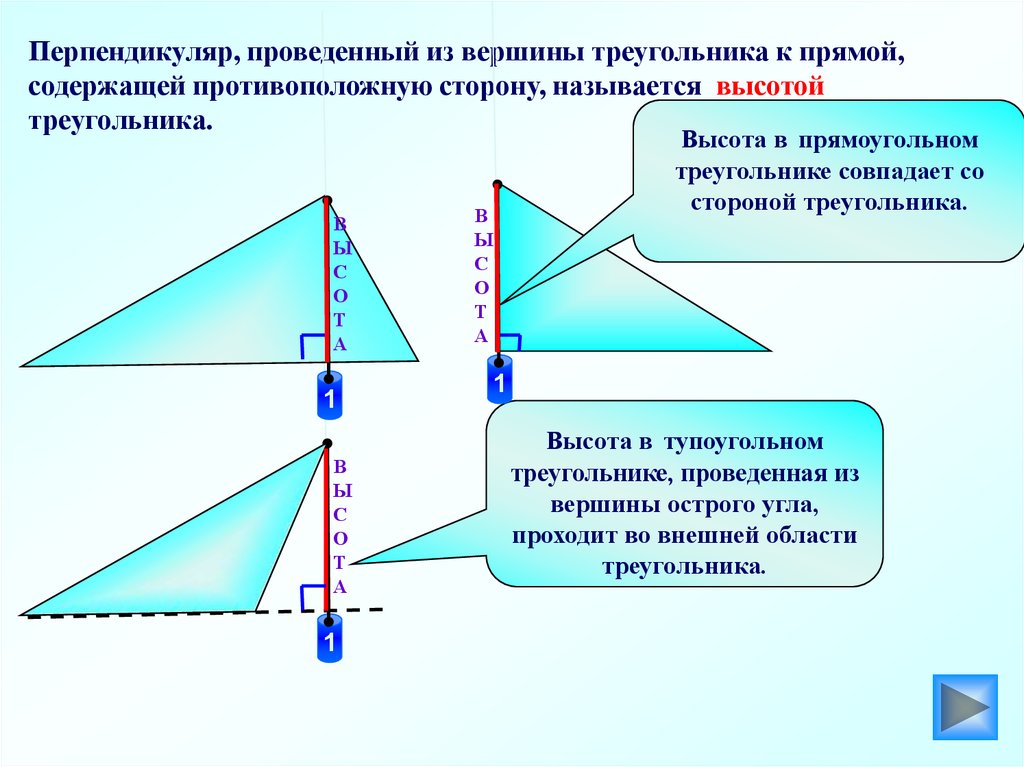
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
Высота в прямоугольном
треугольнике совпадает со
стороной треугольника.
1
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.

5.

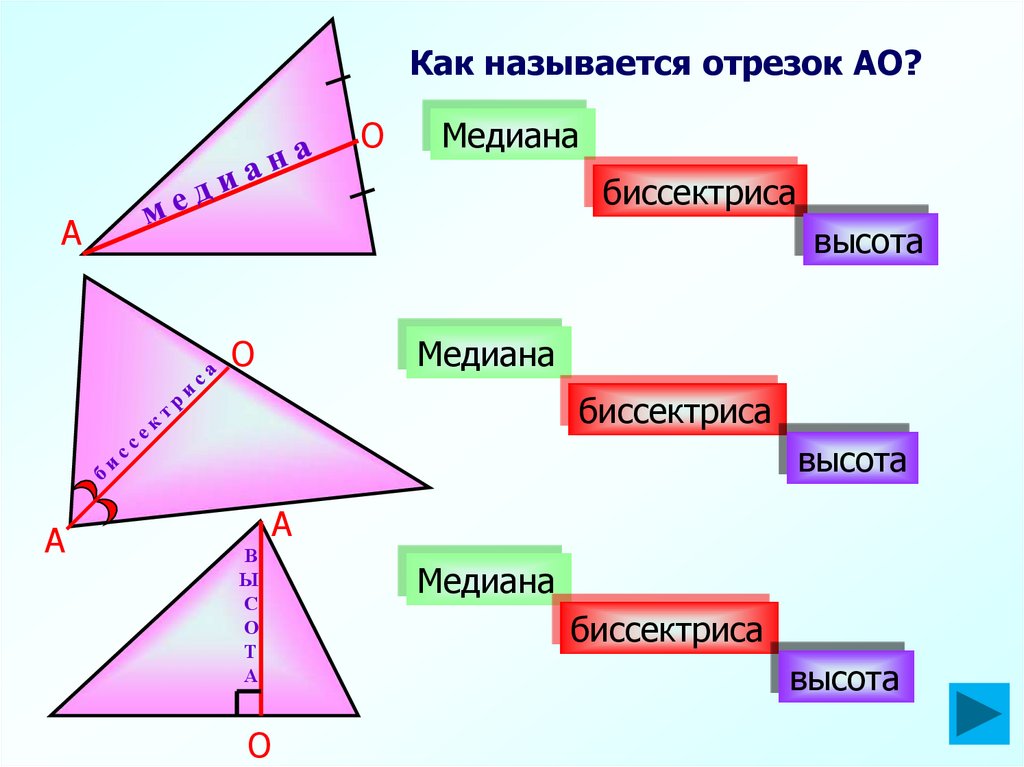
Как называется отрезок АО?
О
Медиана
биссектриса
А
высота
О
Медиана
биссектриса
высота
А
А
В
Ы
С
О
Т
А
О
Медиана
биссектриса
высота

6.

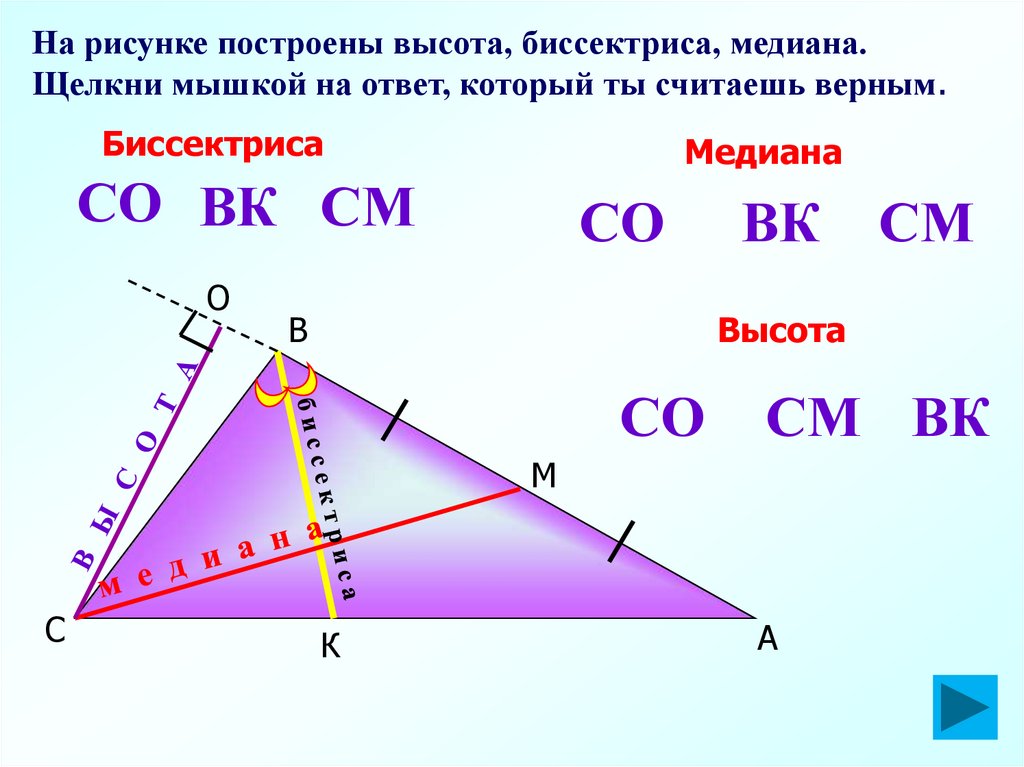
На рисунке построены высота, биссектриса, медиана.
Щелкни мышкой на ответ, который ты считаешь верным.
Биссектриса
Медиана
СО ВК СМ
О
СО
В
ВК
Высота
СО
СМ ВК
М
С
СМ
К
А

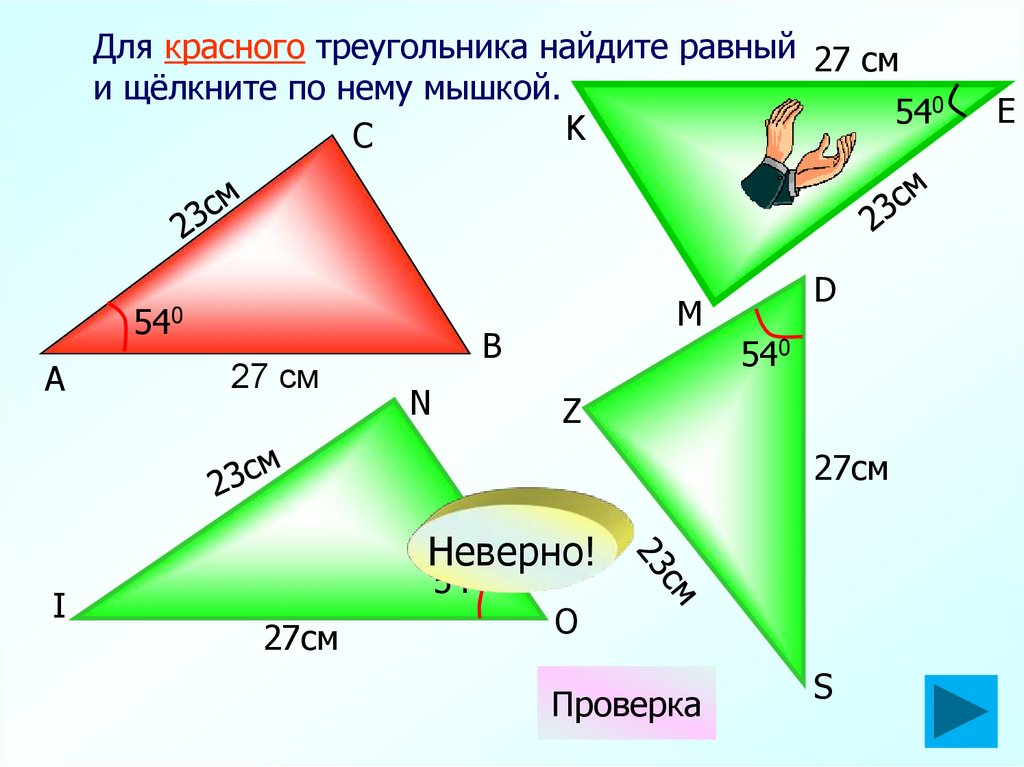
7.

Для красного треугольника найдите равный 27 см
и щёлкните по нему мышкой.
0
54
K
C
540
А
27 см
M
B
N
D
540
Z
27см
I
Неверно!
0
54
27см
O
Проверка
S
E

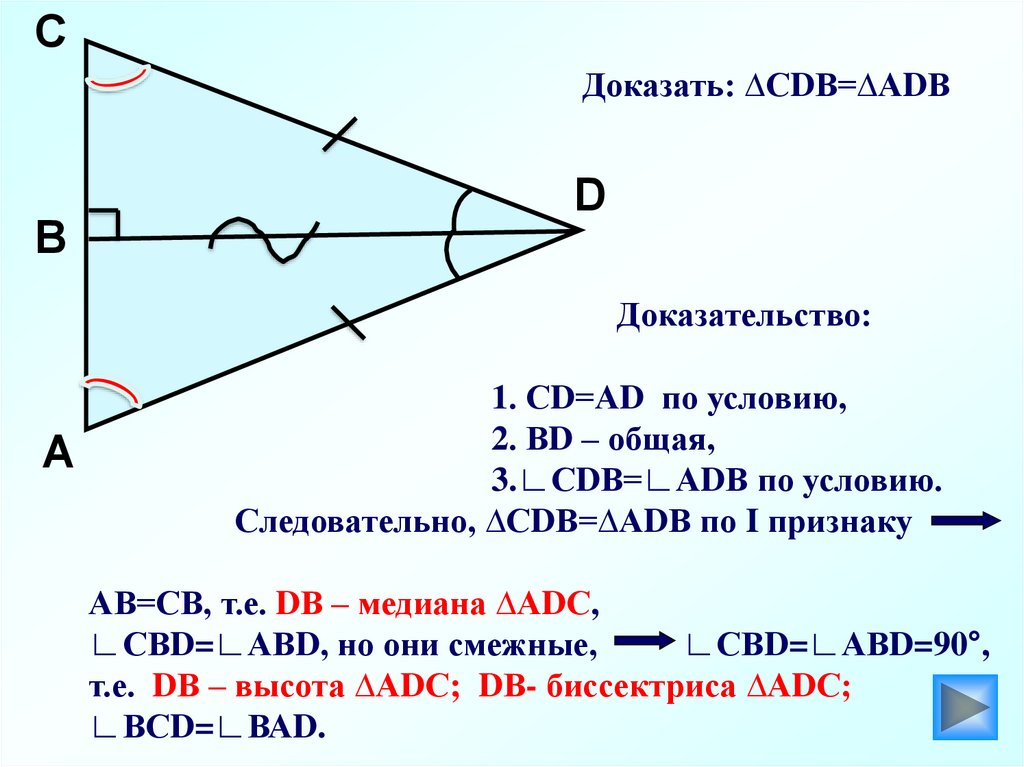
8.

C
Доказать: ∆СDВ=∆АDВ
В
D
Доказательство:
А
1. СD=АD по условию,
2. ВD – общая,
3.∟СDВ=∟АDВ по условию.
Следовательно, ∆СDВ=∆АDВ по I признаку
АВ=СВ, т.е. DВ – медиана ∆АDС,
∟СВD=∟АВD, но они смежные,
∟СВD=∟АВD=90°,
т.е. DВ – высота ∆АDС; DВ- биссектриса ∆АDС;
∟ВСD=∟ВАD.

9.

Равнобедренный треугольник
А
АВС р / б
АВ АС
В
ОснованиеС

10. Равносторонний треугольник

P
∆МNP- р/с
MN=NP =MP
M
N

11.

Начиная игру в бильярд, необходимо расположить шары в
виде треугольника. Для этого используют специальную
треугольную рамку.

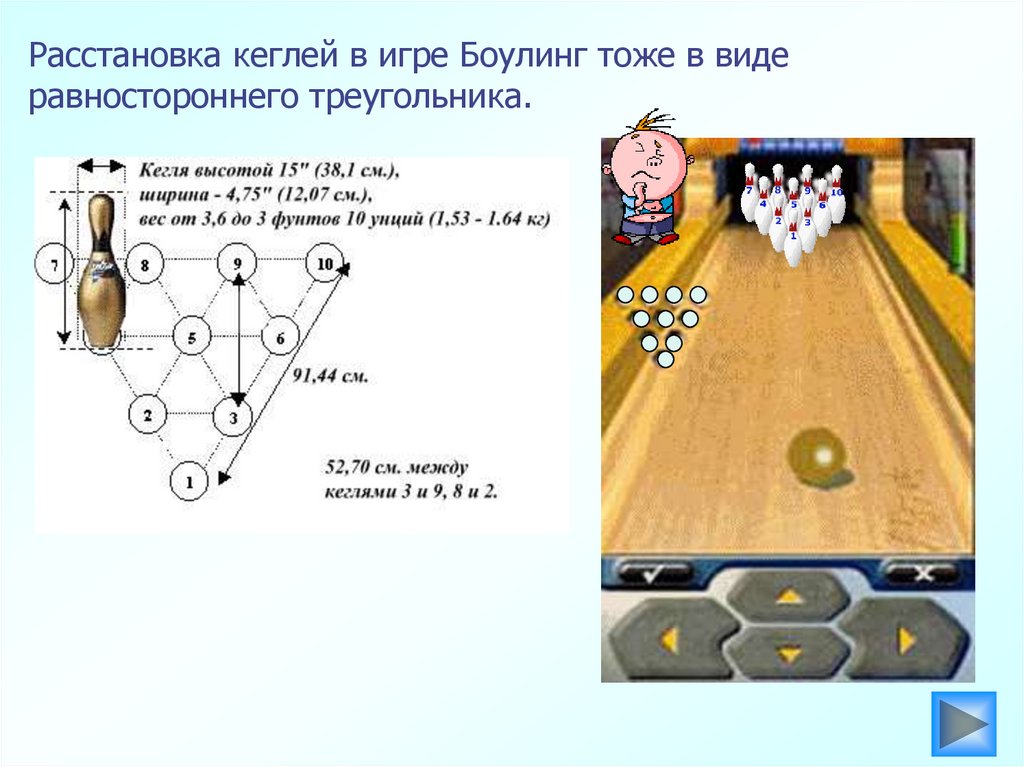
12.

Расстановка кеглей в игре Боулинг тоже в виде
равностороннего треугольника.

13.

Треугольники в конструкции мостов.
Высоковольтные линии
электропередачи.
Треугольники делают
конструкции надежными

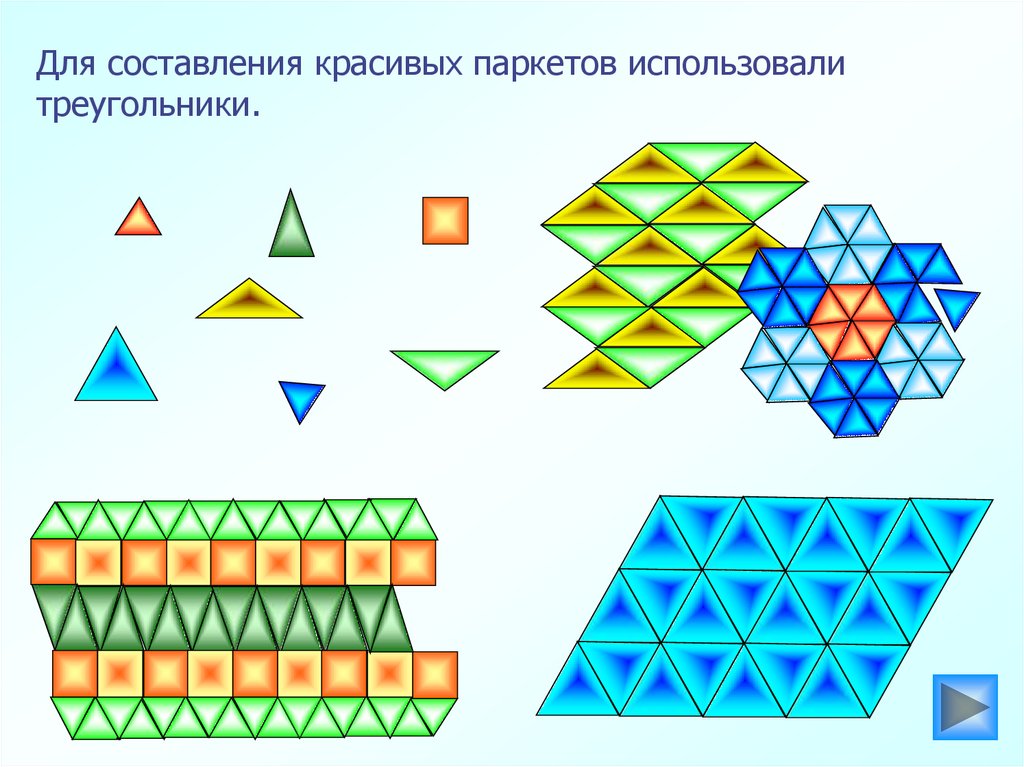
14.

Для составления красивых паркетов использовали
треугольники.

15.

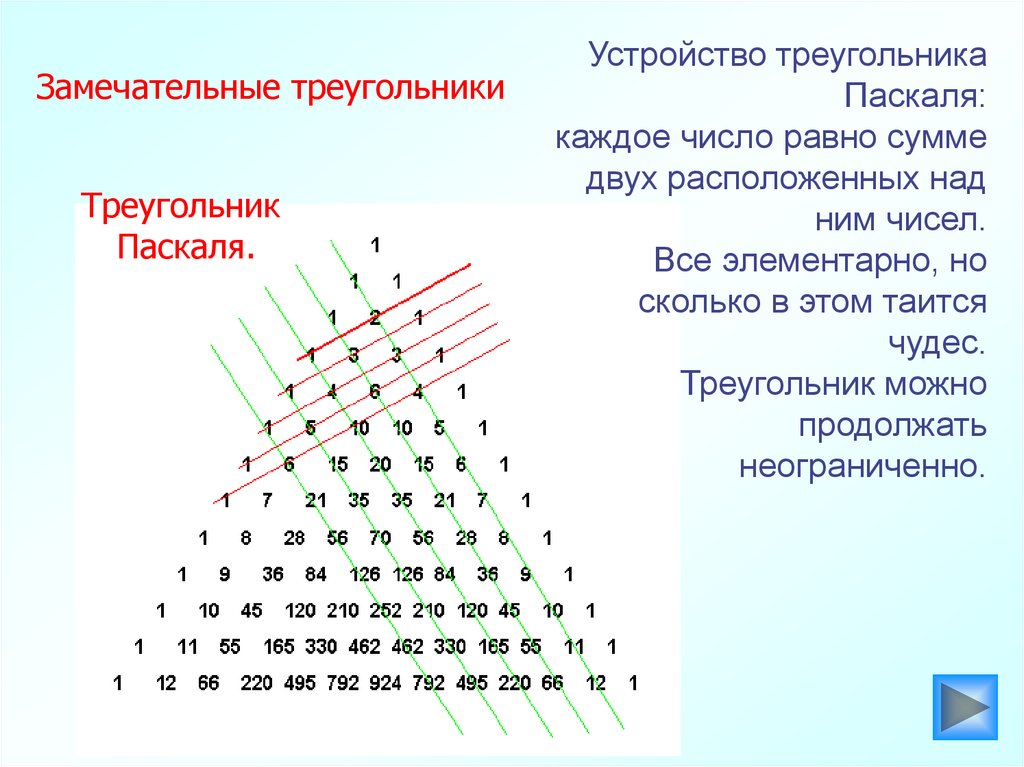
Замечательные треугольники
Треугольник
Паскаля.
Устройство треугольника
Паскаля:
каждое число равно сумме
двух расположенных над
ним чисел.
Все элементарно, но
сколько в этом таится
чудес.
Треугольник можно
продолжать
неограниченно.

16.

Треугольник Паскаля компьютер перевёл на язык цвета.

17.

18.

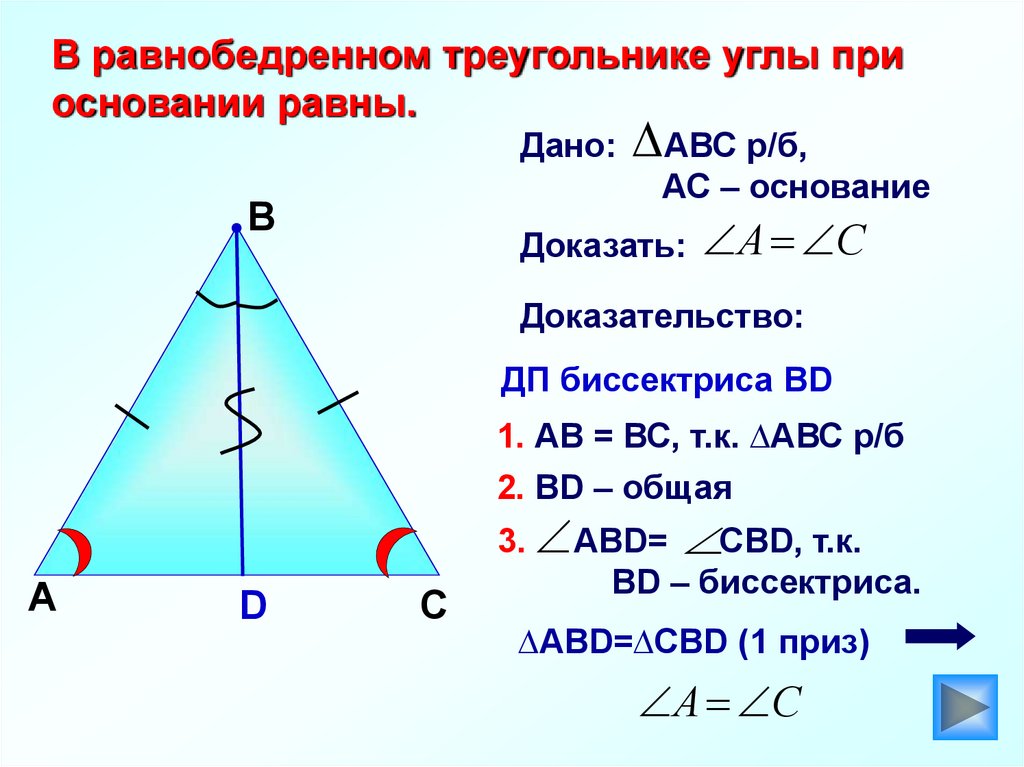
В равнобедренном треугольнике углы при
основании равны.
Дано:
АВС р/б,
АС – основание
В
Доказать:
А С
Доказательство:
ДП биссектриса ВD
1. АВ = ВС, т.к. ∆АВС р/б
2. ВD – общая
А
D
С
3. ABD= СВD, т.к.
ВD – биссектриса.
∆АВD=∆СBD (1 приз)
А С

19.

∆АВС равнобедренный. Для угла В найди
равный и щелкни по нему мышкой!
ВЕРНО!
А
Подумай!
С
В равнобедренном
треугольнике углы при
основании равны.
∠В=∠А
В
Проверка

20.

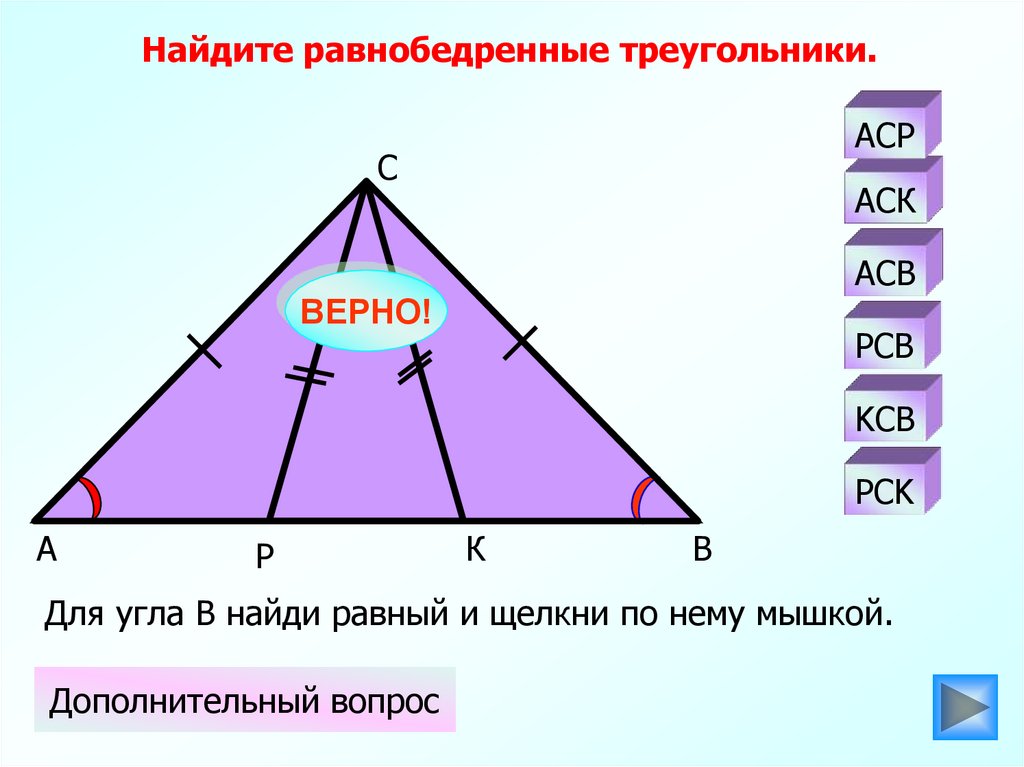
Найдите равнобедренные треугольники.
АСР
С
АСК
АСВ
ВЕРНО!
PCB
KCB
PCK
А
Р
К
В
Для угла В найди равный и щелкни по нему мышкой.
Дополнительный вопрос

21.

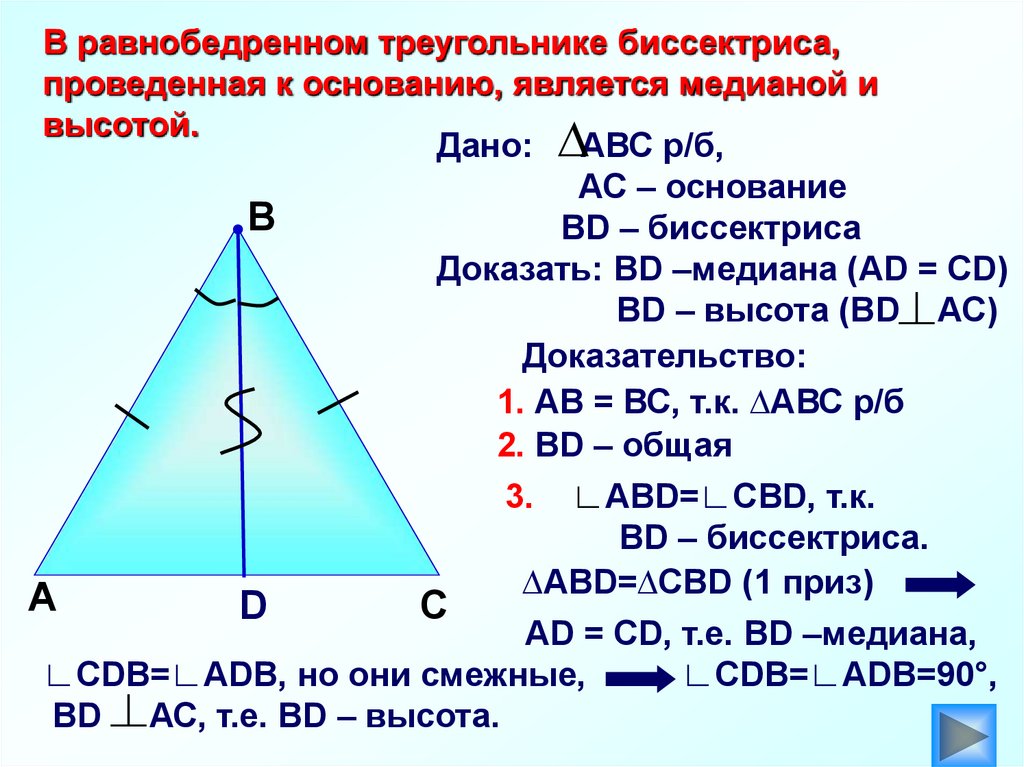
В равнобедренном треугольнике биссектриса,
проведенная к основанию, является медианой и
высотой.
Дано: АВС р/б,
АС – основание
В
ВD – биссектриса
Доказать: ВD –медиана (АD = СD)
ВD – высота (ВD АС)
Доказательство:
1. АВ = ВС, т.к. ∆АВС р/б
2. ВD – общая
3. ∟ABD=∟СВD, т.к.
ВD – биссектриса.
∆АВD=∆СBD (1 приз)
А
D
С
АD = СD, т.е. ВD –медиана,
∟СDВ=∟АDВ, но они смежные,
∟СDВ=∟АDВ=90°,
ВD АС, т.е. ВD – высота.

22.

107. В равнобедренном треугольнике основание в 2 раза
меньше боковой стороны, а периметр равен50см. Найдите
стороны треугольника.
В
Дано: ∆ABC-р/б, АВ=ВС=2АС, Р=50см.
Найти: АВ, ВС, АС.
2х
2х
Решение. ∆ABC –р/б с основанием АС.
Тогда АВ = 2х см,
С
х
ВС =2х см.
Составим уравнение:
Пусть АС = х см.
А
Х+2х+2х=50
5х=50
Х=10 - сторона АС.
АВ=ВС=20см.
Ответ: 20см, 20см,10см.
Р=50см

23.

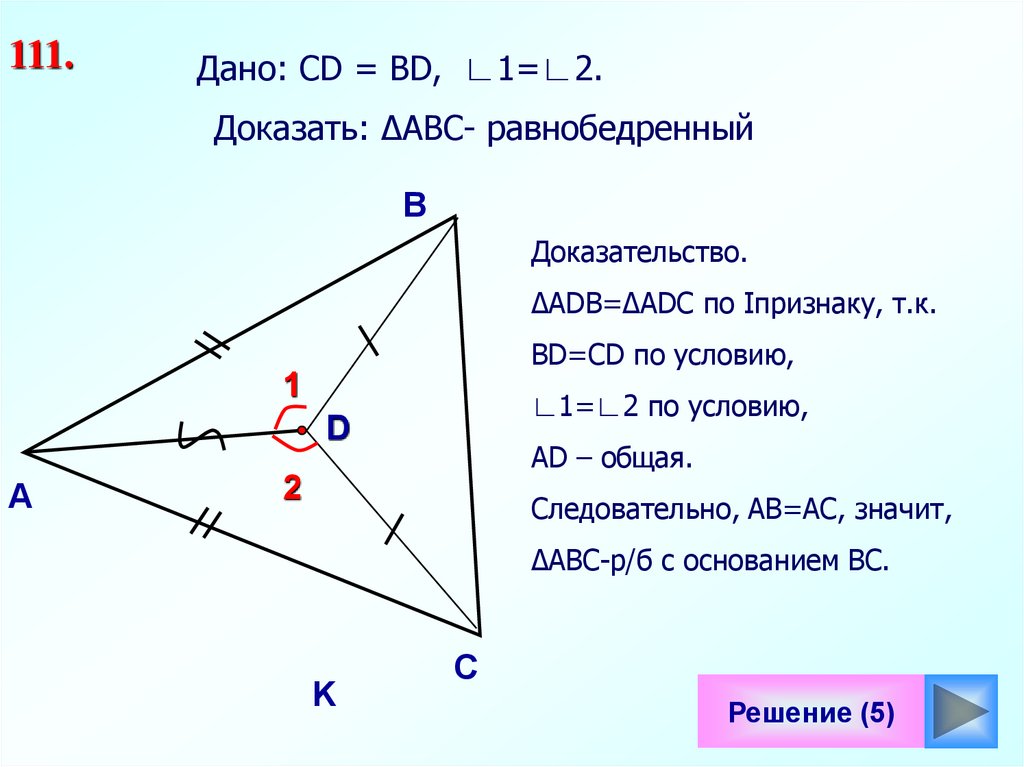
111.
Дано: СD = ВD, ∟1=∟2.
Доказать: ∆АВС- равнобедренный
B
Доказательство.
∆АDВ=∆АDС по Iпризнаку, т.к.
ВD=СD по условию,
1
∟1=∟2 по условию,
D
А
АD – общая.
2
Следовательно, АВ=АС, значит,
∆АВС-р/б с основанием ВС.
K
С
Решение (5)

24.

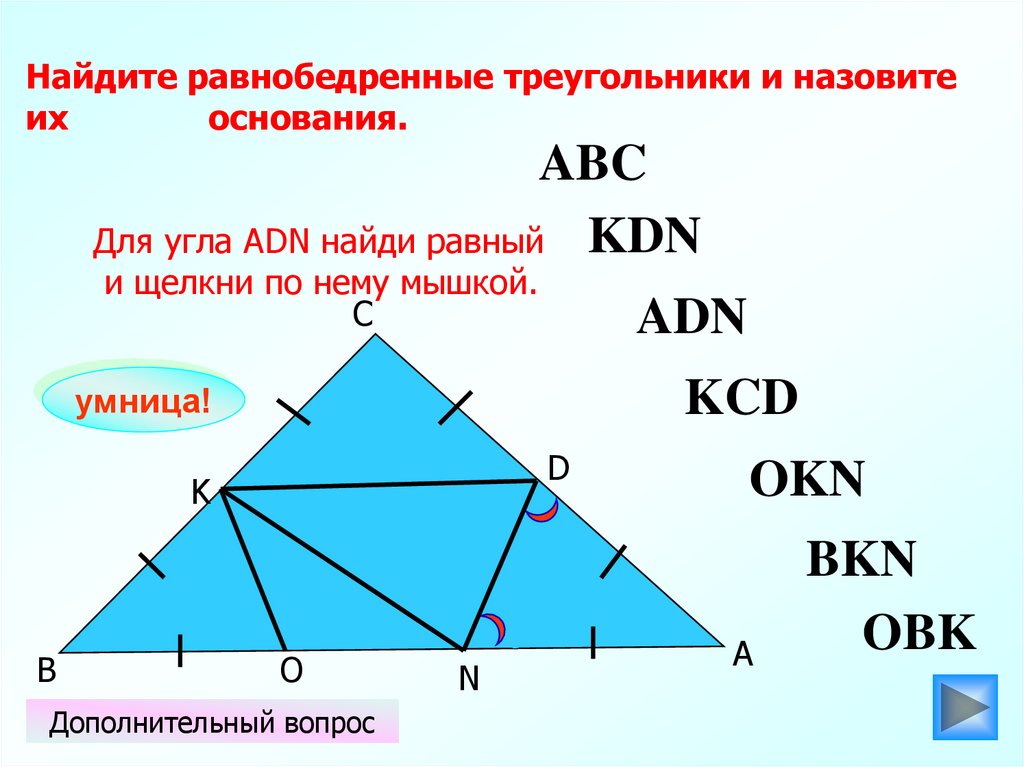
Найдите равнобедренные треугольники и назовите
их
основания.
ABC
Для угла АDN найди равный KDN
и щелкни по нему мышкой.
С
ADN
KCD
умница!
D
K
В
O
Дополнительный вопрос
N
OKN
А
BKN
OBK

25. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

• Углы при основании равны.
• Биссектриса, проведенная к основанию,
является медианой и высотой.
• Медиана, проведенная к основанию. является
биссектрисой и высотой.
• Высота, проведенная к основанию, является
биссектрисой и медианой.

26.

Домашнее задание
П.18, вопросы 10 – 13 стр.50
№№108, 113,117 (свойство
углов р/б ∆)

27. 117. Дано: ∆АВС, АВ=ВС, ∆СЕD, СD=DЕ. Доказать: ∟ВАС=∟СЕD.

Дано: ∆АВС, АВ=ВС,
∆СЕD, СD=DЕ.
Доказать: ∟ВАС=∟СЕD.
117.
В
Доказательство:
1. ∆АВС – р/б
1
А
∟1=∟2.
2 С
3
4
Е 2. ∆CDE- р/б
∟3=∟4,
3. ∟2=∟3 т.к. вертикальные
D
Следовательно, ∟1=∟2=∟3=∟4,
поэтому ∟ВАС=∟СЕD