Similar presentations:
Свойства равнобедренного треугольника
1.
2.
Треугольник называетсяравнобедренным,
В если две его стороны равны
АВС- равнобедренный
АВ, ВС - боковые стороны
АС - основание
А, С – углы при основании
В – угол при вершине
А
С
3.
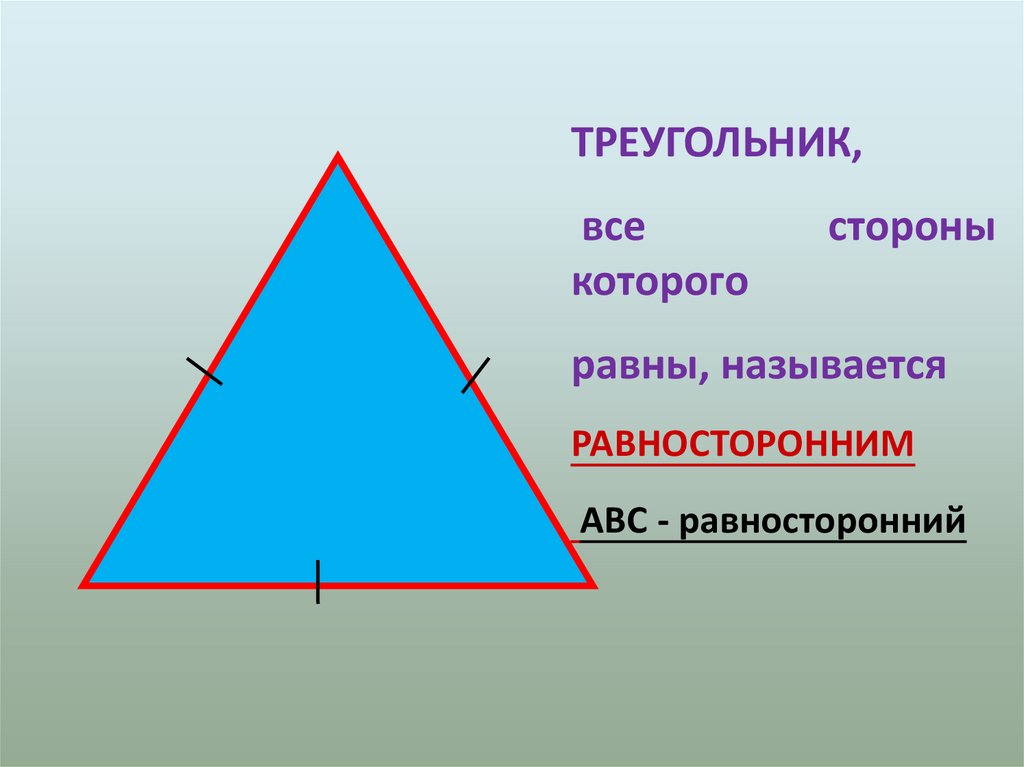
ТРЕУГОЛЬНИК,все
которого
стороны
равны, называется
РАВНОСТОРОННИМ
АВС - равносторонний
4.
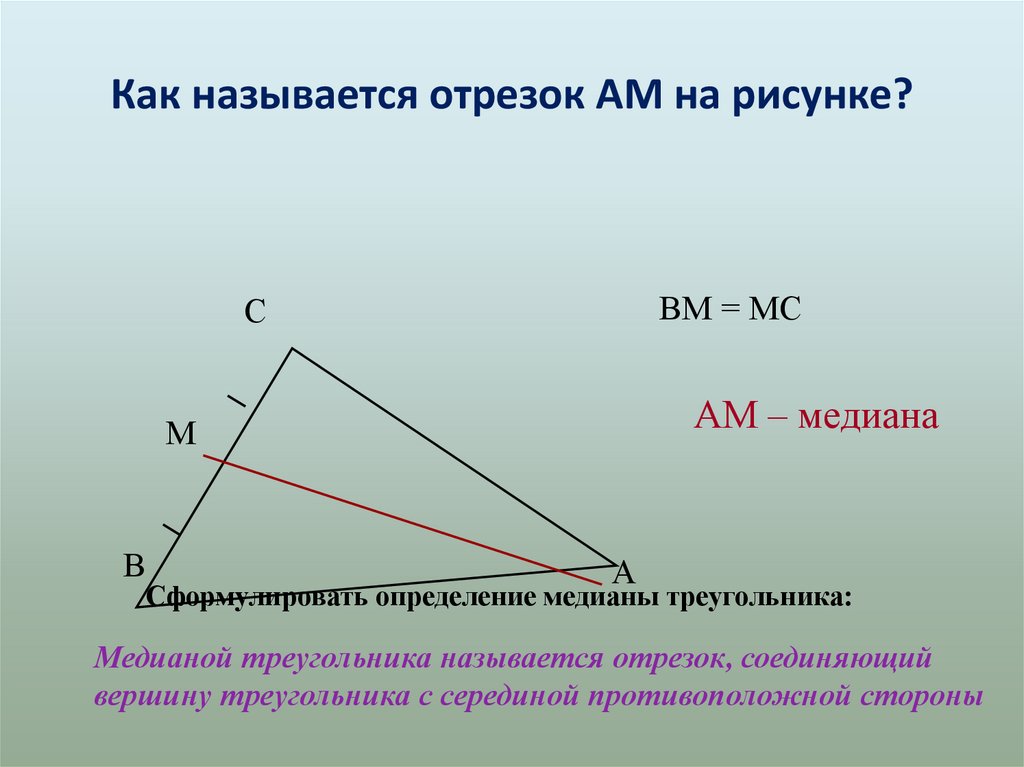
Как называется отрезок АМ на рисунке?ВМ = МС
С
АМ – медиана
М
В
А
Сформулировать определение медианы треугольника:
Медианой треугольника называется отрезок, соединяющий
вершину треугольника с серединой противоположной стороны
5.
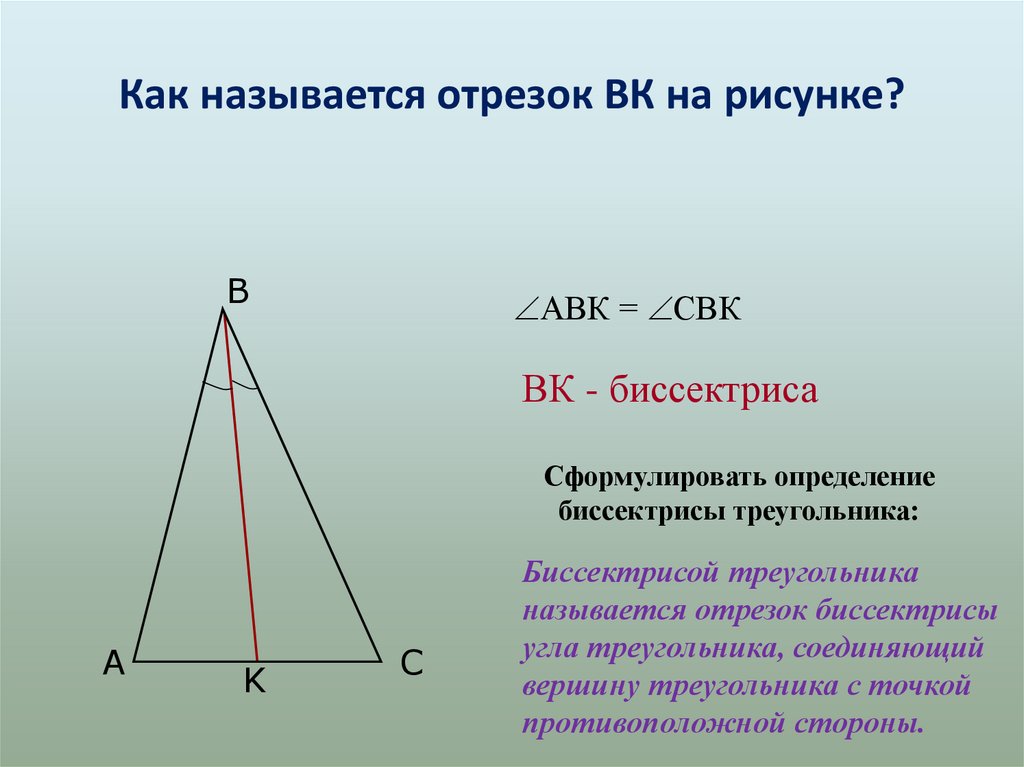
Как называется отрезок ВК на рисунке?B
АВК = СВК
ВК - биссектриса
Сформулировать определение
биссектрисы треугольника:
A
K
C
Биссектрисой треугольника
называется отрезок биссектрисы
угла треугольника, соединяющий
вершину треугольника с точкой
противоположной стороны.
6.
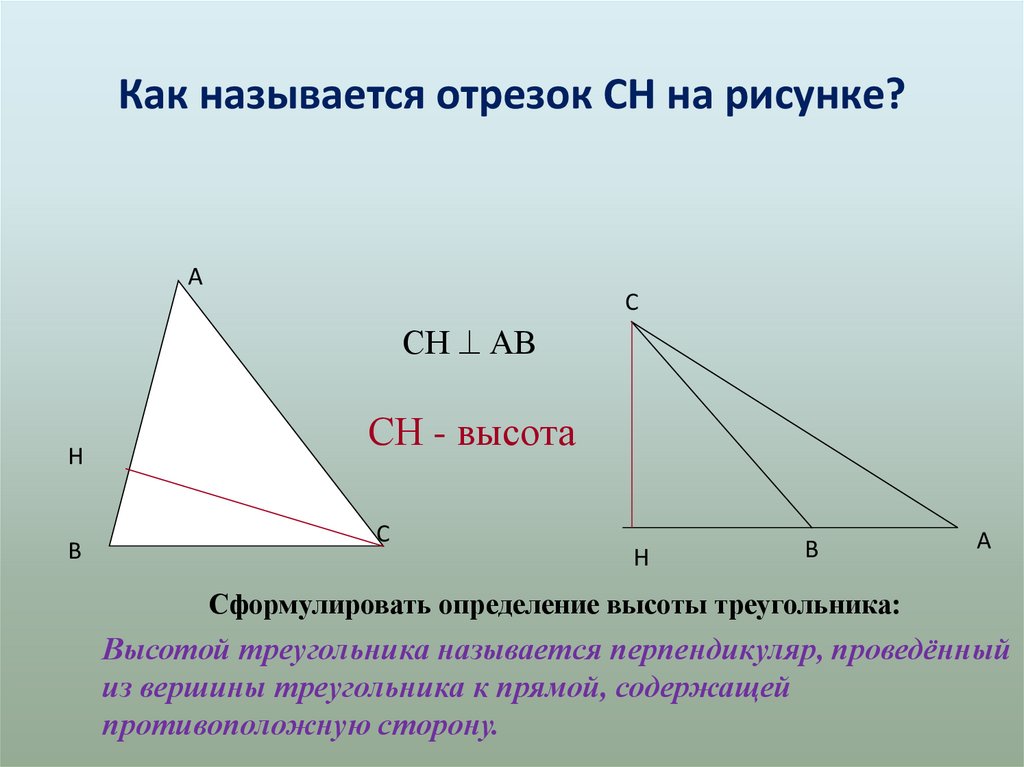
Как называется отрезок СН на рисунке?A
C
СН АВ
H
B
СН - высота
C
H
B
A
Сформулировать определение высоты треугольника:
Высотой треугольника называется перпендикуляр, проведённый
из вершины треугольника к прямой, содержащей
противоположную сторону.
7.
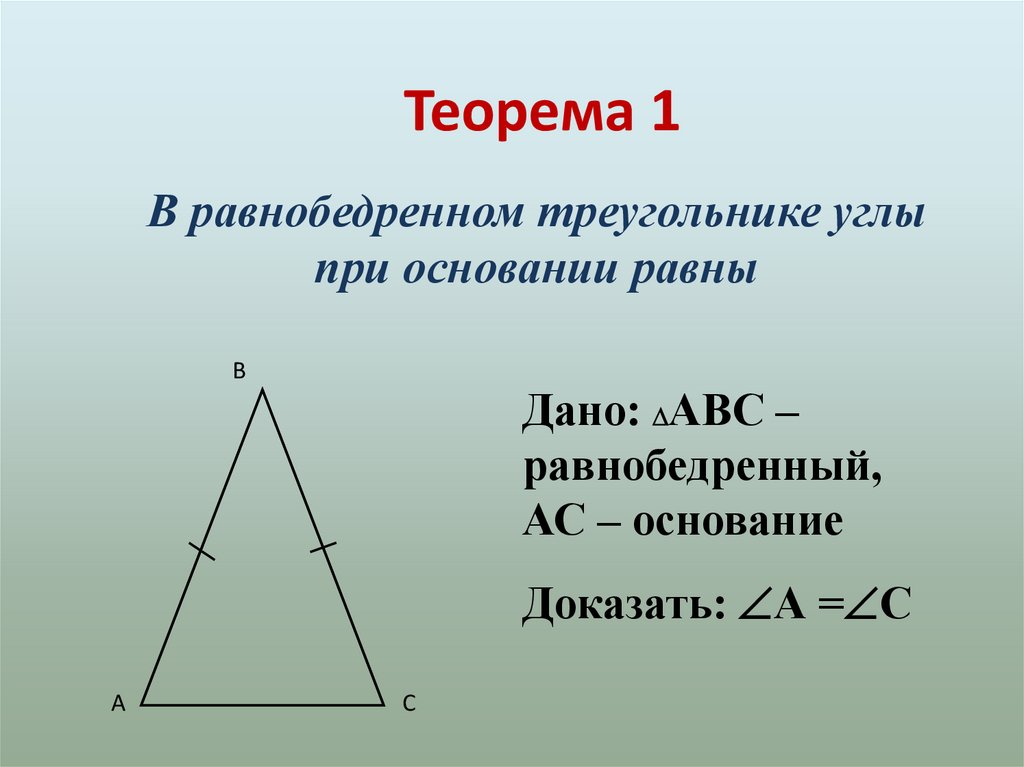
Теорема 1В равнобедренном треугольнике углы
при основании равны
B
Дано: АВС –
равнобедренный,
АС – основание
Доказать: А = С
A
C
8.
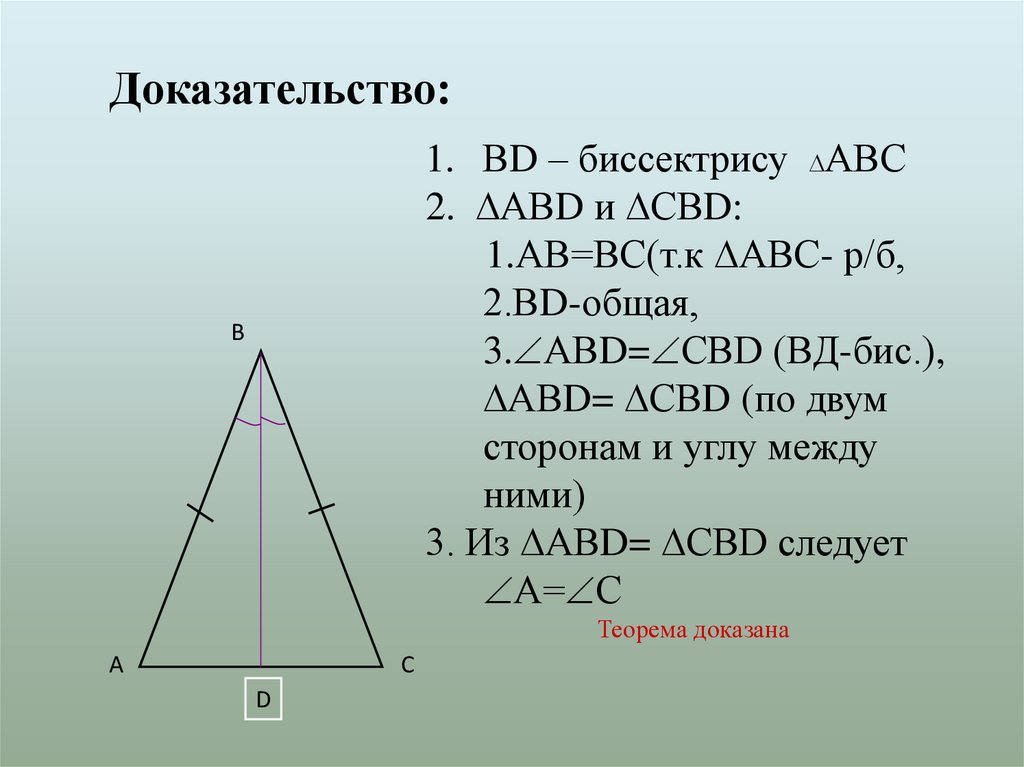
Доказательство:1. ВD – биссектрису АВС
2. АВD и СВD:
1.АВ=ВС(т.к АВС- р/б,
2.ВD-общая,
3. АВD= СВD (ВД-бис.),
АВD= СВD (по двум
сторонам и углу между
ними)
3. Из АВD= СВD следует
А= С
B
Теорема доказана
A
C
D
9.
Теорема 2В равнобедренном треугольнике биссектриса,
проведённая к основанию,
является медианой и высотой
B
Дано: АВС –равнобедренный,
АС – основание,
ВD – биссектриса.
Доказать: 1. ВD – медиана
A
C
D
2. ВD – высота
10.
Доказательство:B
A
3 4
D
C
1. Рассмотрим АВD и СВD:
АВ=ВС, ВD-общая, АВD= СВD,
значит АВD= СВD (по двум
сторонам и углу между ними)
2. Отсюда, АD=DC, значит D –
середина АС, следовательно
ВD – медиана
3. 3= 4 и 3 и 4 – смежные,
значит 3 = 4 = 180:2=90°,
следовательно ВD АС , т.е.
ВD – высота
Теорема доказана
11.
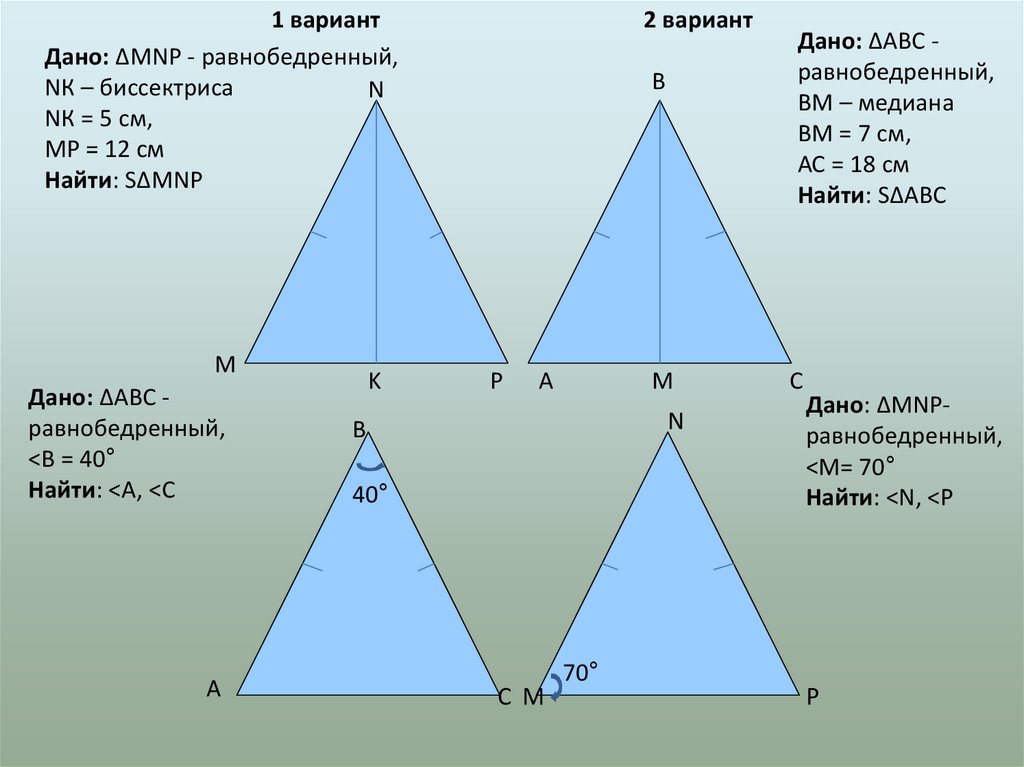
1 вариантДано: ∆MNP - равнобедренный,
NК – биссектриса
N
NК = 5 см,
MP = 12 см
Найти: S∆MNP
М
Дано: ∆АВС равнобедренный,
<B = 40°
Найти: <A, <С
A
K
2 вариант
B
P
A
M
N
B
40°
C М
70°
Дано: ∆АВС равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
C
Дано: ∆MNPравнобедренный,
<М= 70°
Найти: <N, <P
P
12.
1 вариантДано: ∆MNP - равнобедренный,
NК – биссектриса
N
NК = 5 см,
MP = 12 см
Найти: S∆MNP
2 вариант
B
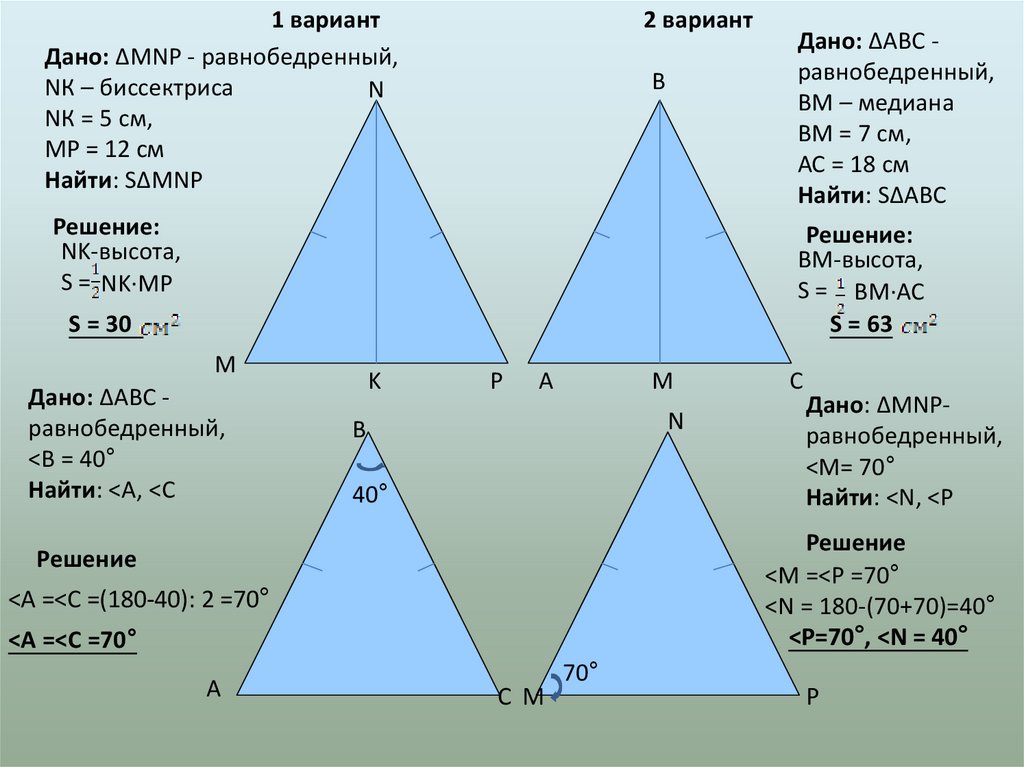
Решение:
NK-высота,
S = NK·MP
Дано: ∆АВС равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
Решение:
ВМ-высота,
S = ВМ·АС
S = 63
S = 30
М
Дано: ∆АВС равнобедренный,
<B = 40°
Найти: <A, <С
K
P
A
M
N
B
40°
Дано: ∆MNPравнобедренный,
<М= 70°
Найти: <N, <P
Решение
<М =<Р =70°
<N = 180-(70+70)=40°
<P=70°, <N = 40°
Решение
<А =<С =(180-40): 2 =70°
<А =<С =70°
A
C
C М
70°
P
13.
П. 18 учить теоремы,№108,110,112 – из учебника
Дополнительная задача:
Доказать, что в равнобедренном
треугольнике медиана,
проведённая к основанию
является биссектрисой и высотой.





 mathematics
mathematics








