Равнобедренный треугольник и его свойства

1. Равнобедренный треугольник и его свойства.

2. Как называется отрезок АМ на рисунке?

ВМ = МС
С
М
В
АМ – медиана
А
Сформулировать определение медианы треугольника:
Медианой треугольника называется отрезок, соединяющий
вершину треугольника с серединой противоположной стороны

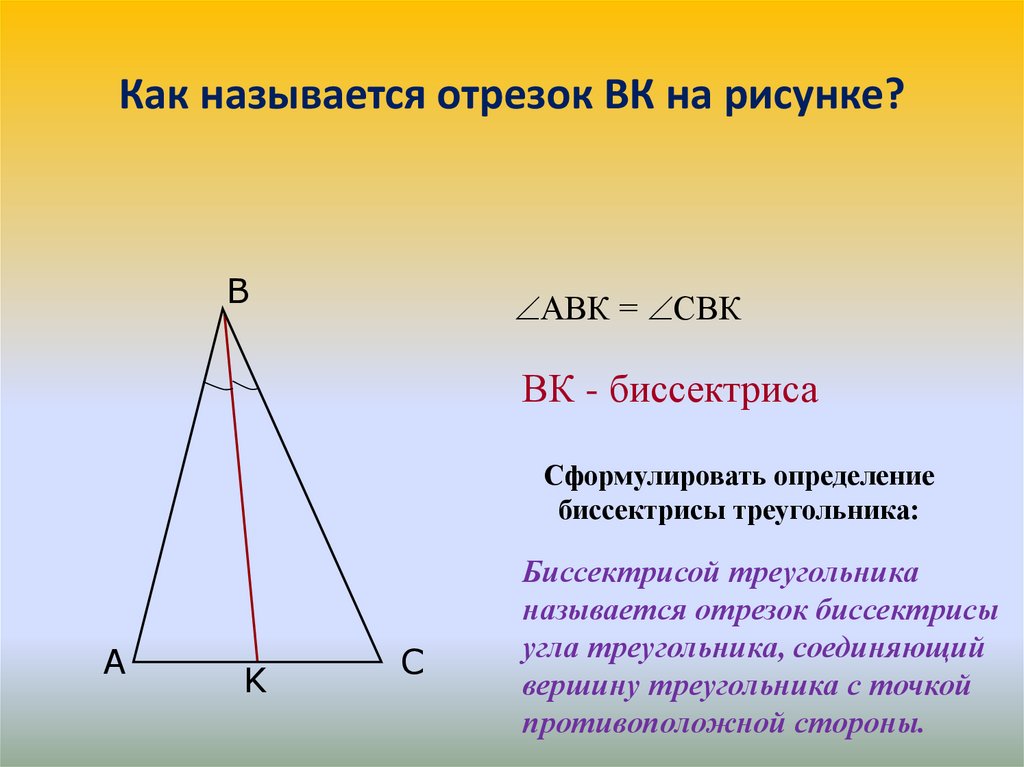
3. Как называется отрезок ВК на рисунке?

B
АВК = СВК
ВК - биссектриса
Сформулировать определение
биссектрисы треугольника:
A
K
C
Биссектрисой треугольника
называется отрезок биссектрисы
угла треугольника, соединяющий
вершину треугольника с точкой
противоположной стороны.

4. Как называется отрезок СН на рисунке?

A
C
СН АВ
H
B
СН - высота
C
H
B
A
Сформулировать определение высоты треугольника:
Высотой треугольника называется перпендикуляр, проведённый
из вершины треугольника к прямой, содержащей
противоположную сторону.

5.

Треугольник называется
равнобедренным,
В если две его стороны равны
АВ, ВС - боковые стороны
равнобедренного треугольника
АС - основание равнобедренного
треугольника
А, С – углы при основании
равнобедренного треугольника
В – угол при вершине
А
С
равнобедренного треугольника

6. Назовите основание и боковые стороны данных треугольников

М
O
D
Р
C
N
E
1)
3)
S
2)
H
L
T
4)
F
K
5)
M
C

7.

ТРЕУГОЛЬНИК,
все стороны
которого
равны, называется
РАВНОСТОРОННИМ

8.

9.

1 вариант
Дано: ∆MNP - равнобедренный,
NК – биссектриса
N
NК = 5 см,
MP = 12 см
Найти: S∆MNP
М
Дано: ∆АВС равнобедренный,
<B = 40°
Найти: <A, <С
A
K
2 вариант
B
P
A
M
N
B
40°
C М
70°
Дано: ∆АВС равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
C
Дано: ∆MNPравнобедренный,
<М= 70°
Найти: <N, <P
P

10.

1 вариант
Дано: ∆MNP - равнобедренный,
NК – биссектриса
N
NК = 5 см,
MP = 12 см
Найти: S∆MNP
2 вариант
B
Решение:
NK-высота,
S = NK·MP
Дано: ∆АВС равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
Решение:
ВМ-высота,
S = ВМ·АС
S = 63
S = 30
М
Дано: ∆АВС равнобедренный,
<B = 40°
Найти: <A, <С
K
P
A
M
N
B
40°
Дано: ∆MNPравнобедренный,
<М= 70°
Найти: <N, <P
Решение
<М =<Р =70°
<N = 180-(70+70)=40°
<P=70°, <N = 40°
Решение
<А =<С =(180-40): 2 =70°
<А =<С =70°
A
C
C М
70°
P