Similar presentations:
Свойства равнобедренного треугольника. Решение задач
1. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА.
2. Теорема. В равнобедренном треугольнике углы при основании равны.
ТЕОРЕМА. В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕУГЛЫ ПРИ ОСНОВАНИИ РАВНЫ.
Дано:∆ABC – равнобедренный,
AC – основание.
B
Доказать: A = C
Доказательство:
1) Проведём биссектрису BD.
2) Рассмотрим ∆ABD и ∆CBD:
AB = BC, так как ∆ ABC – равнобедренный
ABD = CBD , так как BD – биссектриса
А
D
C
BD - общая сторона
∆ABD и ∆CBD по двум сторонам и углу
между ними.
Из равенства треугольников следует,
что A = C
чтд.
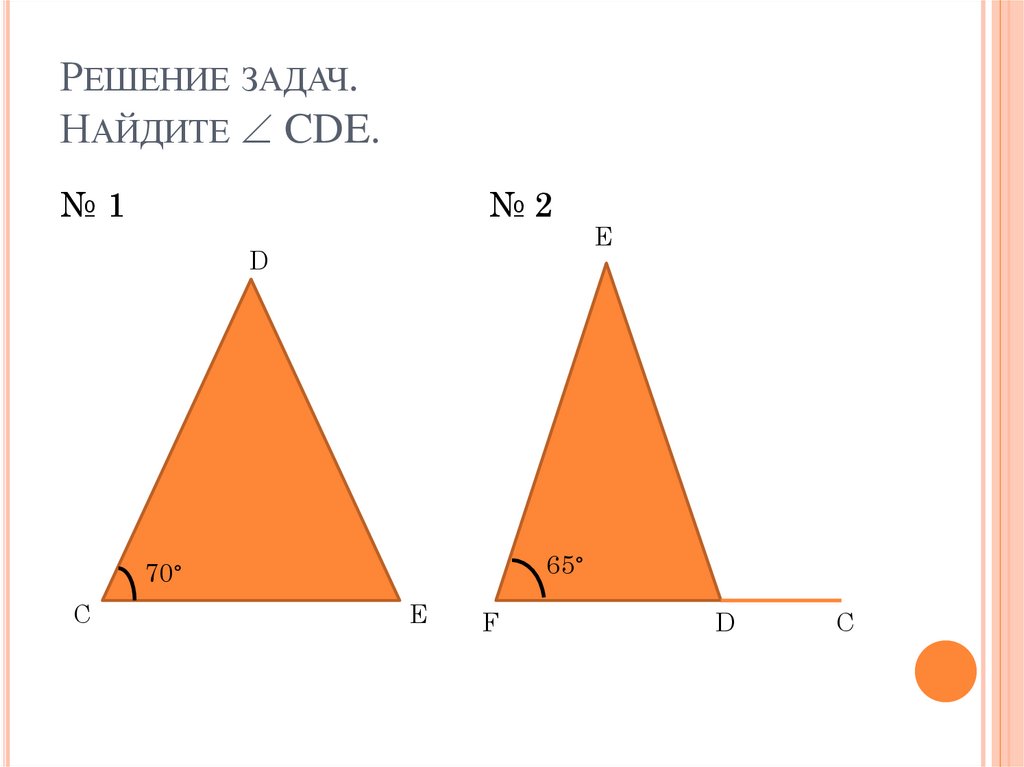
3. Решение задач. Найдите CDE.
РЕШЕНИЕ ЗАДАЧ.НАЙДИТЕ CDE.
№1
№2
D
65°
70°
C
E
E
F
D
C
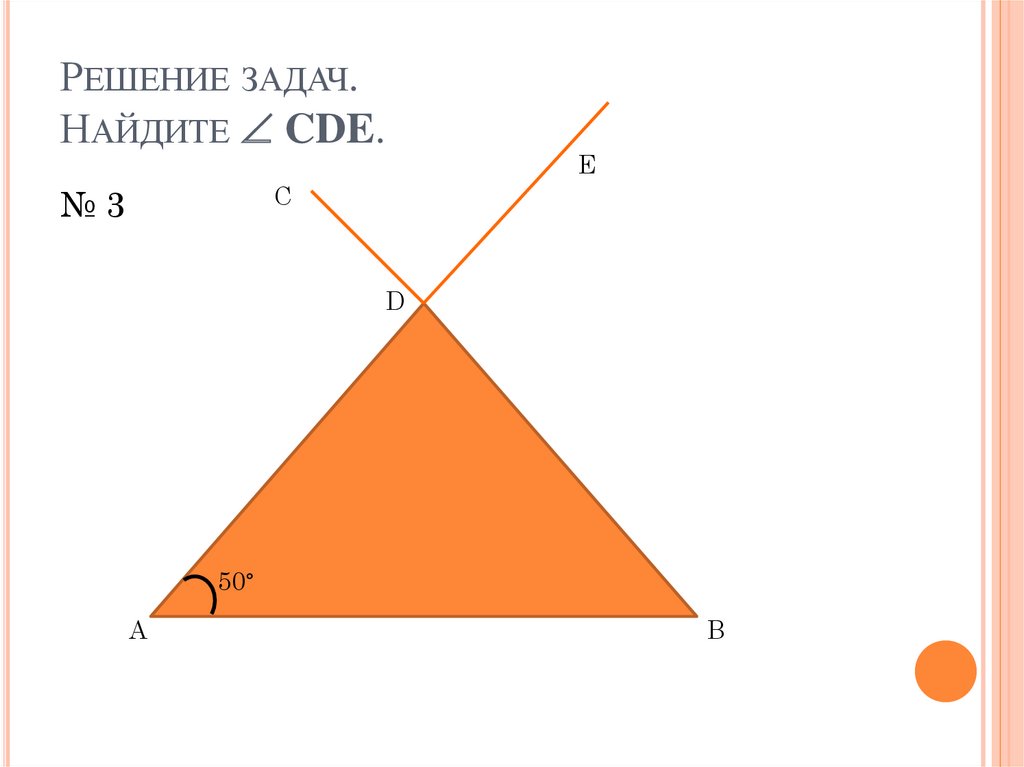
4. Решение задач. Найдите CDE.
РЕШЕНИЕ ЗАДАЧ.НАЙДИТЕ CDE.
E
C
№3
D
50°
A
B
5. Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
ТЕОРЕМА. В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕБИССЕКТРИСА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ,
ЯВЛЯЕТСЯ МЕДИАНОЙ И ВЫСОТОЙ.
Дано:∆ABC – равнобедренный,
BD – биссектриса
Доказать: BD – медиана; BD - высота
Доказательство:
1) Рассмотрим ∆ABD и ∆CBD:
B
A
D
C
∆ABD и ∆CBD по I признаку.
2) Из равенства треугольников следует,
что AD = DC, значит BD –медиана ∆ABC;
ADB = CDB , ADB + CDB = 180° по
свойству смежных углов,
ADB = CDB = 90°, значит BD - высота
∆ABC.
чтд.




 mathematics
mathematics








