Similar presentations:
Параллелепипед
1.
ПАРАЛЛЕЛЕПИПЕД2.
Рассмотрим эти предметыСтроительный
кирпич
Игральный
кубик
Микроволновая
печь
3.
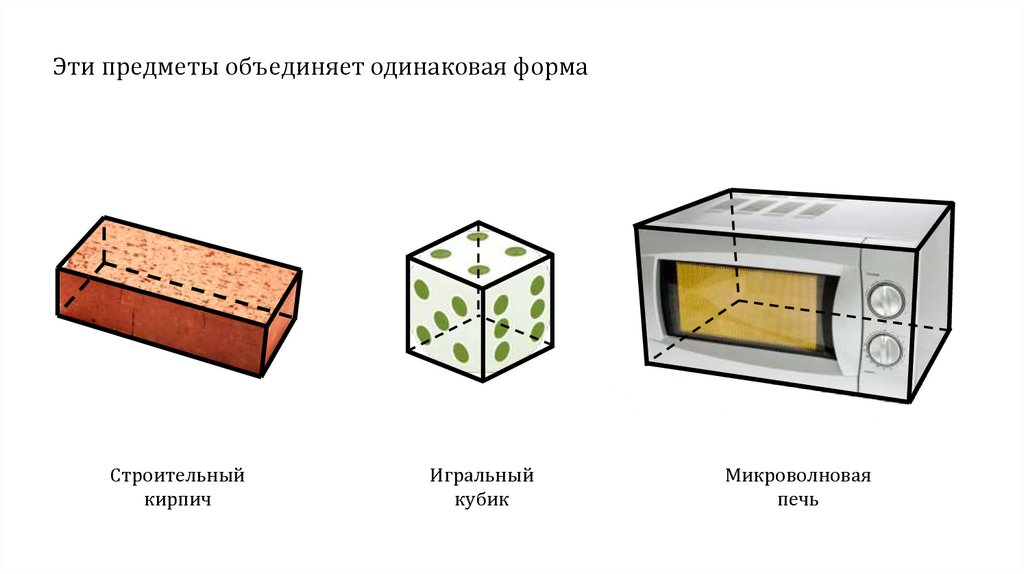
Эти предметы объединяет одинаковая формаСтроительный
кирпич
Игральный
кубик
Микроволновая
печь
4.
D1C1
A1
B1
АВСDА1В1С1D1 —
параллелепипед
D
C
A
B
5.
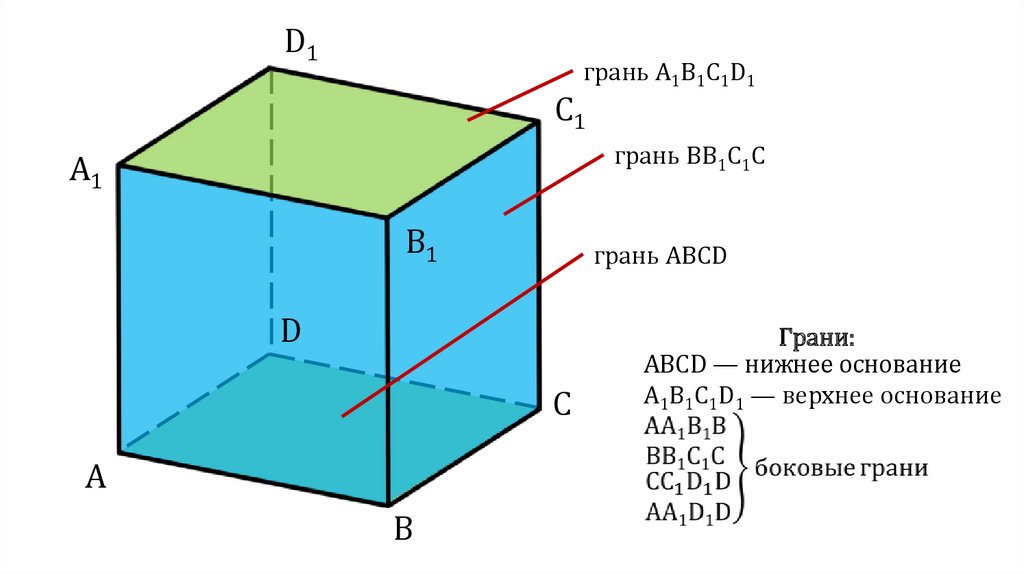
D1грань A1B1C1D1
C1
грань BB1C1C
A1
B1
грань ABCD
D
C
A
B
Грани:
ABCD — нижнее основание
A1B1C1D1 — верхнее основание
6.
D1ребро A1B1
C1
ребро C1C
A1
B1
D
Рёбра:
C
A
ребро AD
B
АВ, ВС, CD, AD, А1В1
В1С1, C1D1, A1D1
АА1, ВВ1, СС1, DD1 —
боковые рёбра
7.
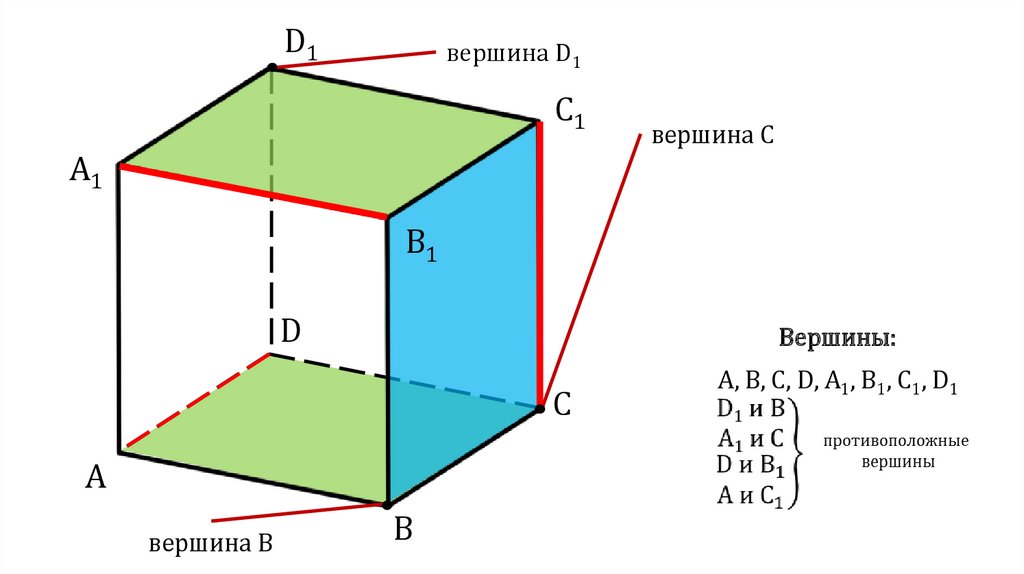
D1вершина D1
C1
вершина С
A1
B1
D
Вершины:
C
A
вершина B
B
А, В, С, D, А1, В1, С1, D1
8.
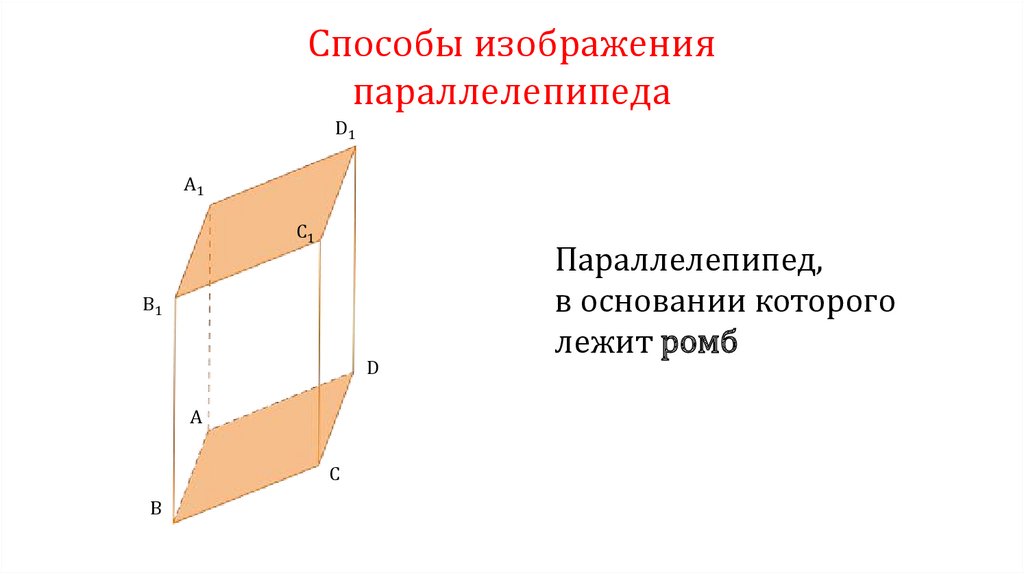
Способы изображенияпараллелепипеда
D1
A1
C1
B1
D
A
C
B
Параллелепипед,
в основании которого
лежит ромб
9.
Способы изображенияпараллелепипеда
D1
A1
C1
B1
A
B
D
C
Параллелепипед,
в основании которого
лежит квадрат
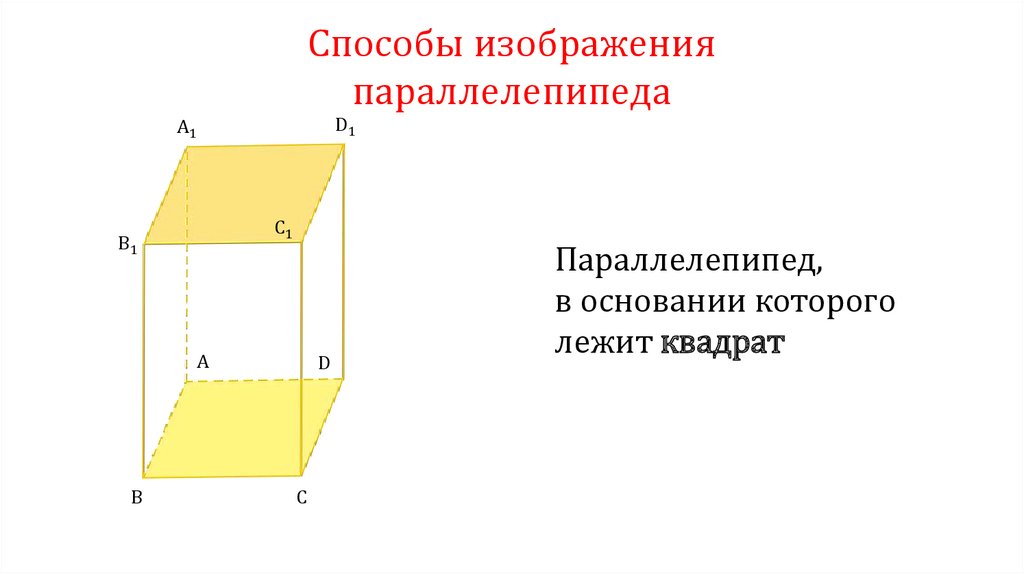
10.
Способы изображенияпараллелепипеда
A1
D1
B1
C1
A
D
B
C
Параллелепипед,
в основании которого
лежит прямоугольник
или параллелограмм
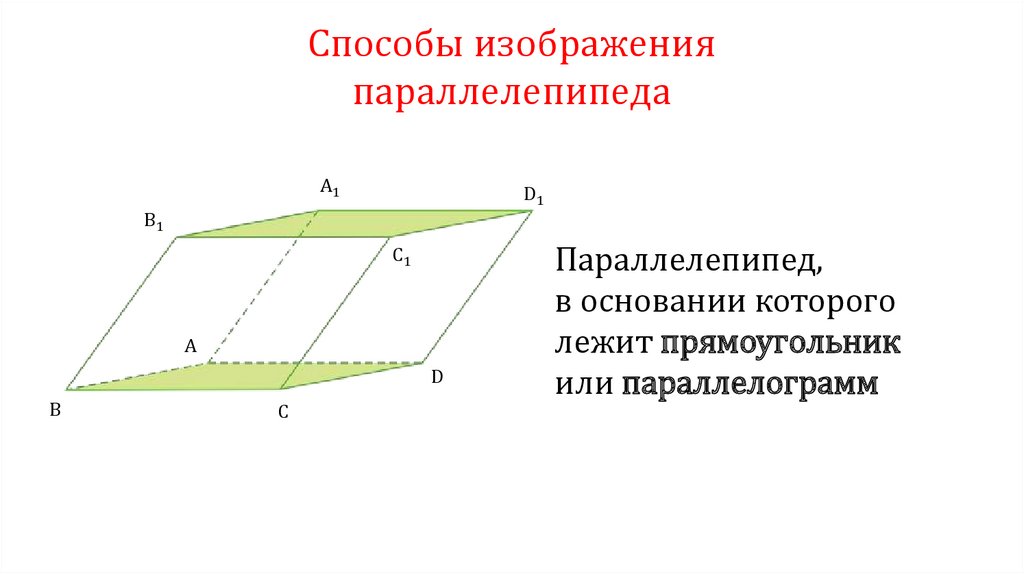
11.
Способы изображенияпараллелепипеда
A1
B1
D1
C1
A
B
Параллелепипед,
у которого все грани —
равные квадраты
D
C
12.
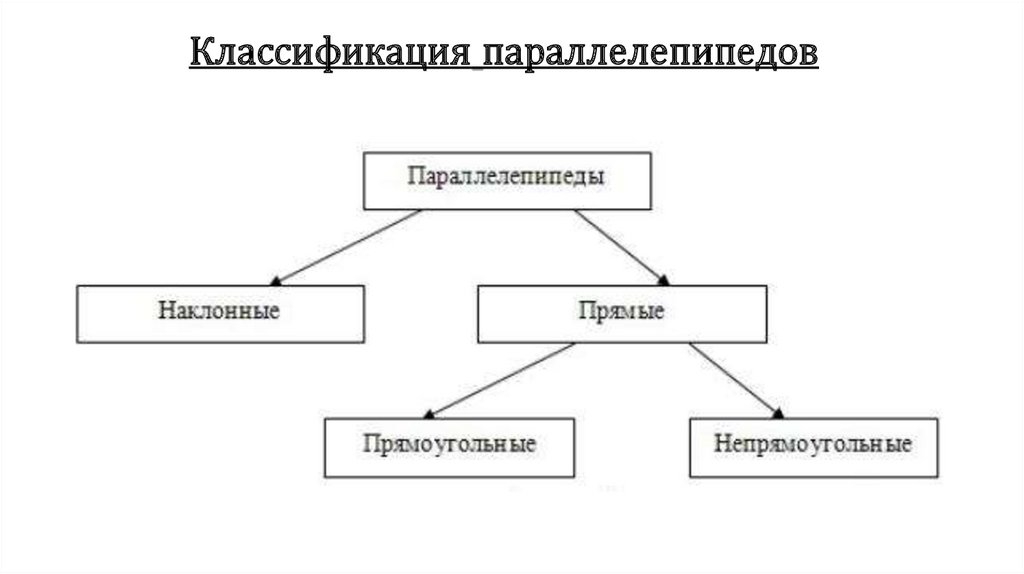
Классификация параллелепипедов13.
Свойство 1Противоположные грани параллелепипеда параллельны
и равны
D1
C1
Дано: АВСDА1В1С1D1 —
B1
параллелепипед
Доказать: свойство 1
A1
Доказательство:
1) АВСD — параллелограмм ⇒ BC ∥ AD
2) АВВ1А1 — параллелограмм ⇒ ВВ1 ∥ AA1
C
D
B
A
4) ВС = АD, ВВ1 = АА1
5) ∠В1ВС = ∠А1АD
Свойство доказано
14.
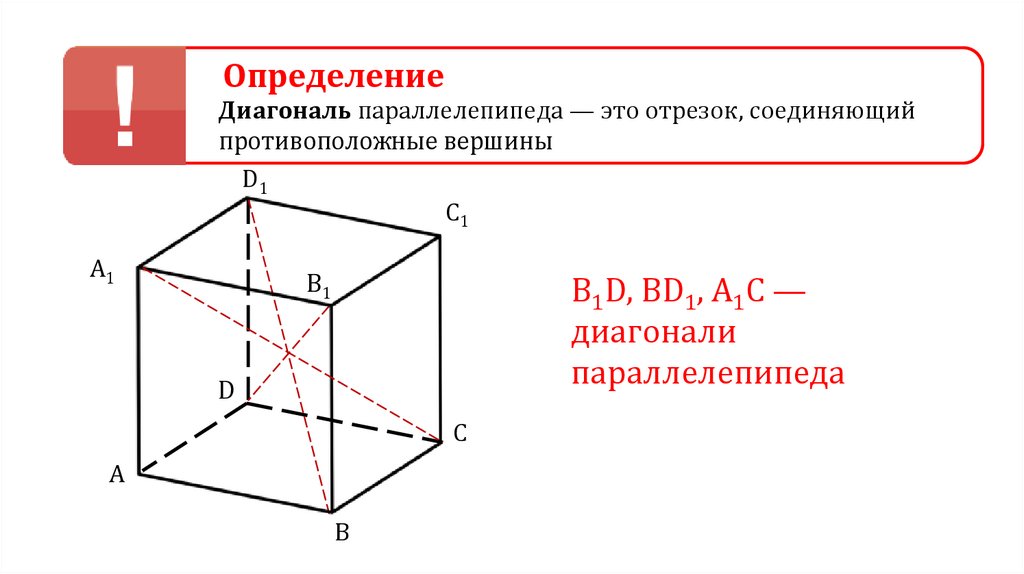
ОпределениеДиагональ параллелепипеда — это отрезок, соединяющий
противоположные вершины
D1
C1
A1
B1
В1D, BD1, А1С —
диагонали
параллелепипеда
D
C
A
B
15.
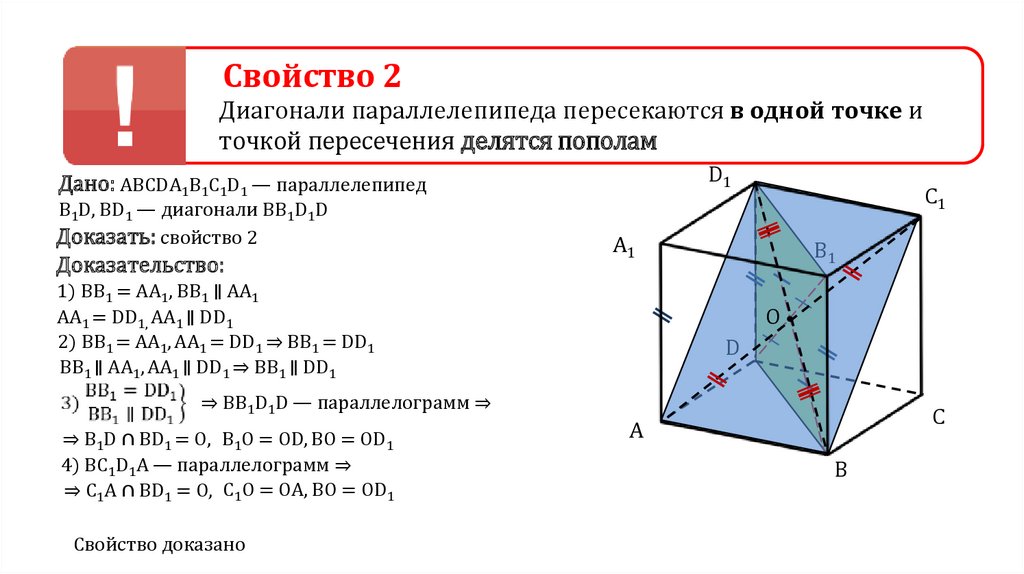
Свойство 2Диагонали параллелепипеда пересекаются в одной точке и
точкой пересечения делятся пополам
D1
Дано: АВСDА1В1С1D1 — параллелепипед
В1D, BD1 — диагонали ВВ1D1D
Доказать: свойство 2
Доказательство:
C1
A1
1) ВB1 = AA1, ВB1 ∥ AA1
АА1 = DD1, АА1 ∥ DD1
2) ВВ1 = АА1, АА1 = DD1 ⇒ ВВ1 = DD1
ВВ1 ∥ АА1, АА1 ∥ DD1 ⇒ ВВ1 ∥ DD1
B1
O
D
⇒ BB1D1D — параллелограмм ⇒
⇒ В1D ∩ BD1 = О, В1О = ОD, BO = OD1
4) BC1D1A — параллелограмм ⇒
⇒ C1A ∩ BD1 = O, C1O = OA, BO = OD1
Свойство доказано
C
A
B
16.
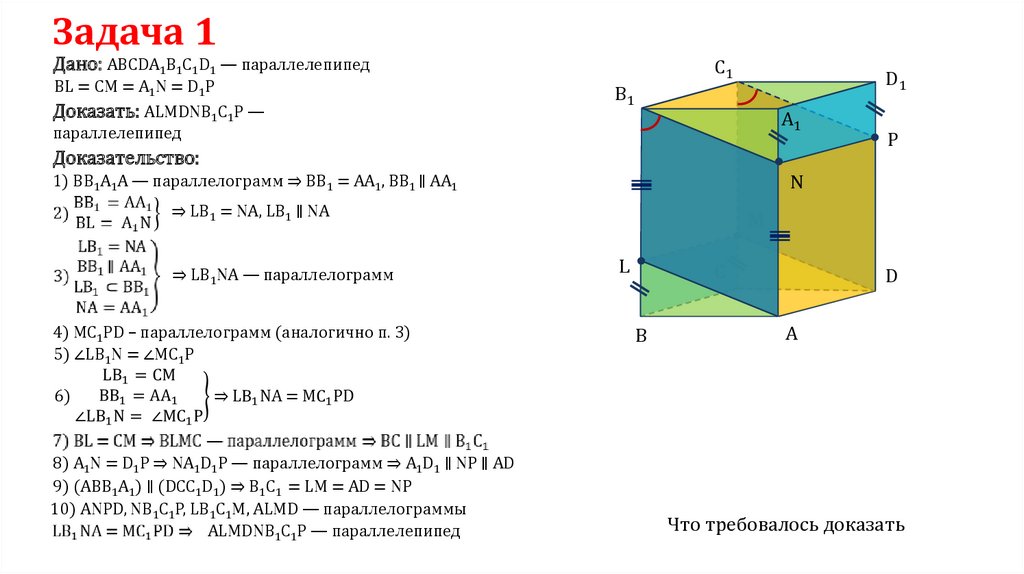
Задача 1Дано: АВСDА1В1С1D1 — параллелепипед
BL = CM = A1N = D1P
Доказать: ALMDNB1C1P —
параллелепипед
C1
D1
B1
A1
Доказательство:
N
1) ВВ1А1А — параллелограмм ⇒ ВВ1 = АА1, ВВ1 ∥ АА1
⇒ LB1 = NA, LB1 ∥ NA
⇒ LB1NA — параллелограмм
4) MC1PD – параллелограмм (аналогично п. 3)
5) ∠LB1N = ∠MC1P
8) A1N = D1P ⇒ NA1D1P — параллелограмм ⇒ A1D1 ∥ NP ∥ AD
9) (ABB1A1) ∥ (DCC1D1) ⇒ B1C1 = LM = AD = NP
10) ANPD, NB1C1P, LB1C1M, ALMD — параллелограммы
ALMDNB1C1P — параллелепипед
P
M
L
C
B
D
A
Что требовалось доказать
17.
Домашнее задание:1. Вопрос 15, №76,78.
2. Творческое задание – создать модель тетраэдра и
параллелепипеда (картон и спицы). На одной из модели
сделать сечение.







 mathematics
mathematics








