Similar presentations:
Сумма углов треугольника
1.
Тема:«Сумма углов
треугольника»
Геометрия 7 класс
учитель Унбаева Г.С.
2. Цель урока: обеспечить усвоение свойства о сумме углов треугольника и умение применять свойство при решении задач
Задачи:1) образовательная: закрепить и проверить знания учащихся по
теме : «Свойство углов образованных при пересечении двух
параллельных прямых третьей и признаки параллельности
прямых»; доказать свойство углов треугольника; формировать
умение применять свойство при решении простейших задач.
2) воспитательная: использовать исторический материал для
развития познавательной активности учащихся.
3) развивающая: развивать внимание и навыки построения
чертежей.
3. План урока:
1. Самостоятельная работа.2. Практическая работа (подготовка к изучения
нового материала).
3. Доказательство теоремы о сумме углов
треугольника (несколько способов).
4. Решение задач (при решении используется
теорема).
4.
Девиз урокаКто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и
скучает.
5.
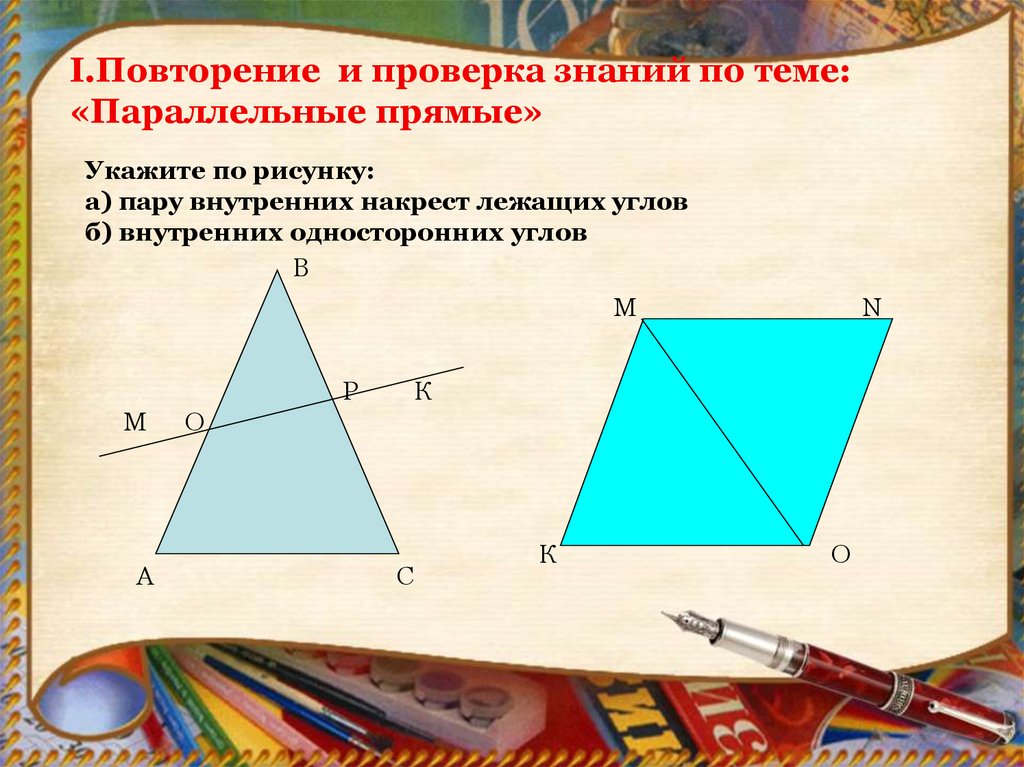
I.Повторение и проверка знаний по теме:«Параллельные прямые»
Укажите по рисунку:
а) пару внутренних накрест лежащих углов
б) внутренних односторонних углов
В
M
Р
М
А
N
К
О
С
К
О
6.
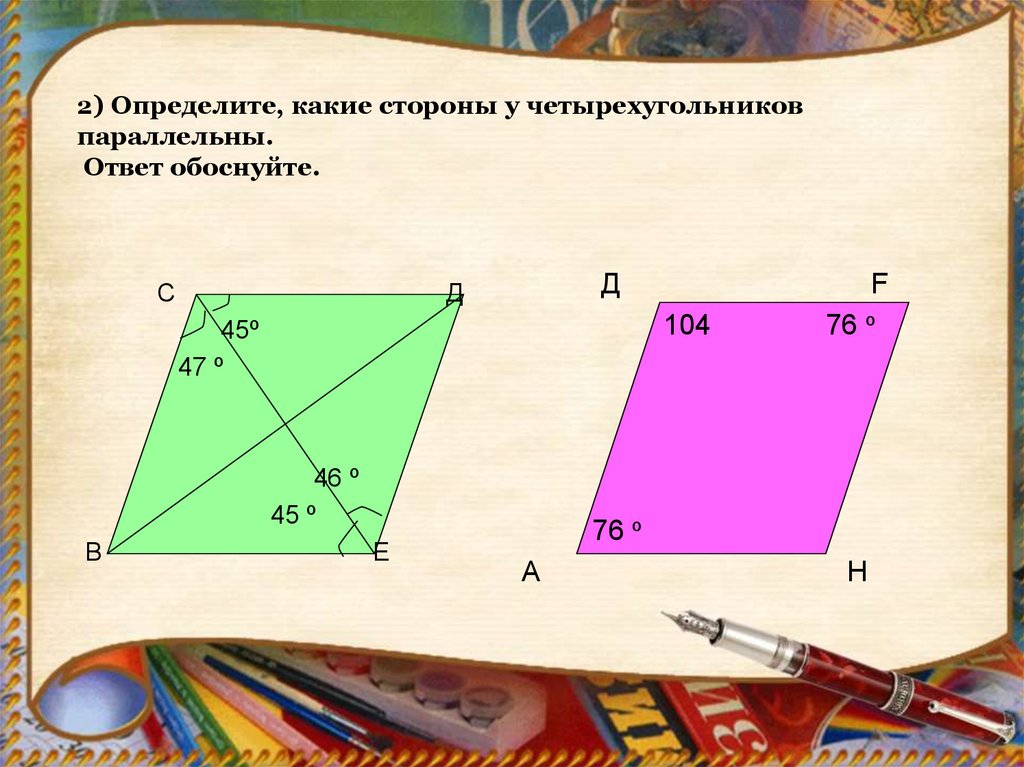
2) Определите, какие стороны у четырехугольниковпараллельны.
Ответ обоснуйте.
С
Д
Д
104
45º
47 º
46 º
45 º
В
F
Е
76 º
76 º
А
Н
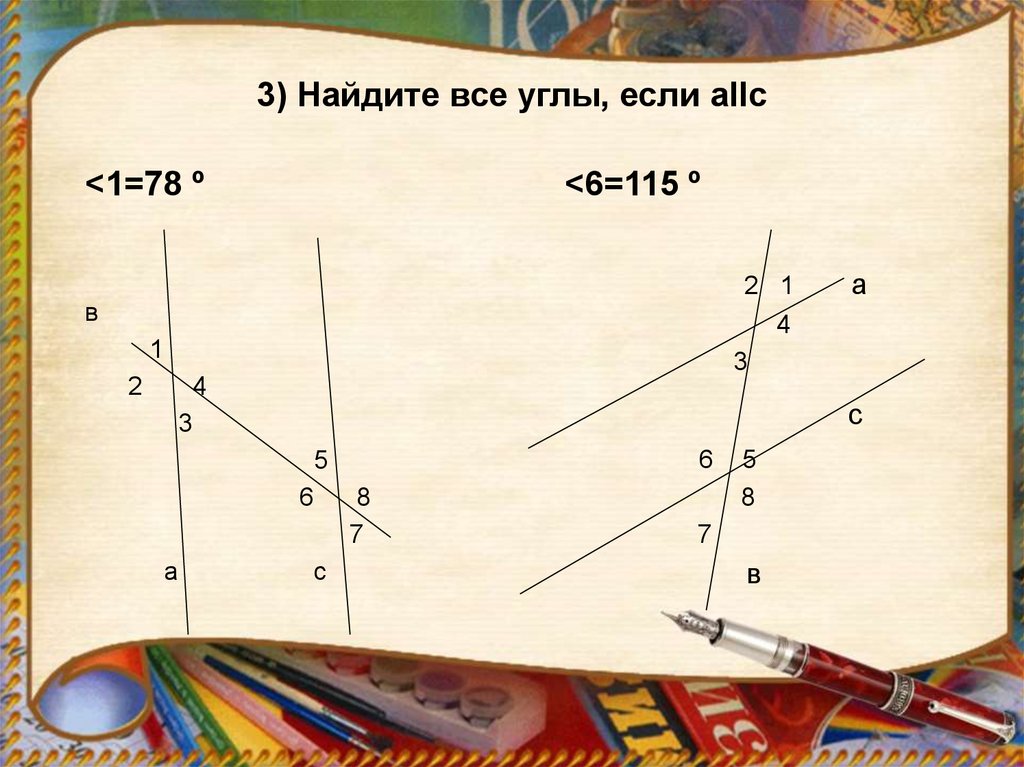
7. 3) Найдите все углы, если аllс
<1=78 º<6=115 º
2 1
в
а
4
1
2
3
4
3
с
5
6
а
с
6
8
7
5
8
7
в
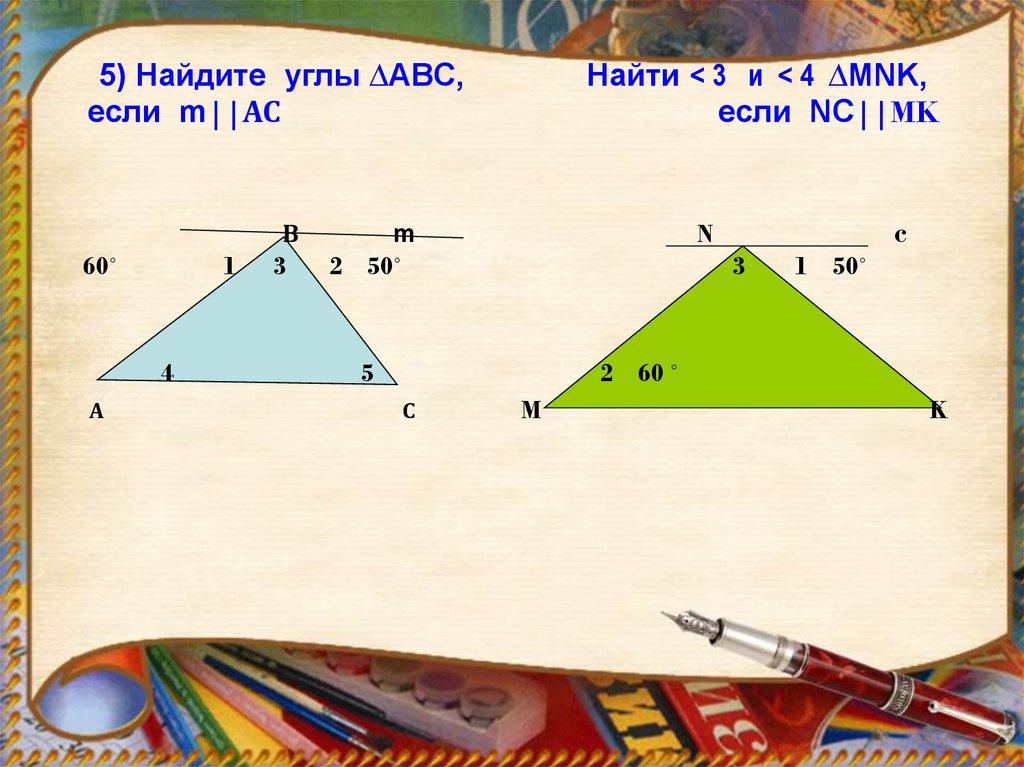
8. 5) Найдите углы ∆АВС, Найти < 3 и < 4 ∆МNK, если m||АС если NC||MK
Найти < 3 и < 4 ∆МNK,если NC||MK
5) Найдите углы ∆АВС,
если m||АС
60˚
1
4
А
В
3
c
N
m
2 50˚
3
5
1 50˚
2 60 ˚
С
M
K
9.
Устная работаВопросы:
1. Сформулируйте определение параллельных прямых.
2. Признаки параллельности прямых.
3. Свойства в.н.углов и в. од. углов при параллельных
прямых и секущей.
4.Решить задачи №5 из самостоятельной работы.
10. Историческая справка
1.Определение параллельных прямых - Евклид (III век дон.э.), в трудах «Начала»
«Параллельные суть прямые, которые находясь в одной
плоскости и будучи продолжены в обе стороны
неограниченно ни с той, ни с другой стороны между собой
не встречаются».
2.Посидоний (I век до н.э.)
«Две прямые, лежащие в одной плоскости,
равноотстоящие друг от друга»
3.Древнегреческий учёный Папп (вторая половина III
века до н.э.) ввёл символ параллельности прямых =.
Впоследствии английский экономист Рикардо (17721823) этот символ использовал как знак равенства.
Только в 18 веке стали использовать символ ||.
11. Открытие свойств углов треугольника.
Древние греки на основе наблюдений и изпрактического опыта делали выводы, высказывали
свои предположения – гипотезы
(Hypotesis – основание, предположение)
а затем на встречах учёных – симпозиумах
(symposium- буквально пиршество, совещание по
какому-либо научному вопросу)
эти гипотезы пытались обосновать и доказать. В то
время сложилось утверждение : «В споре
рождается истина»
12.
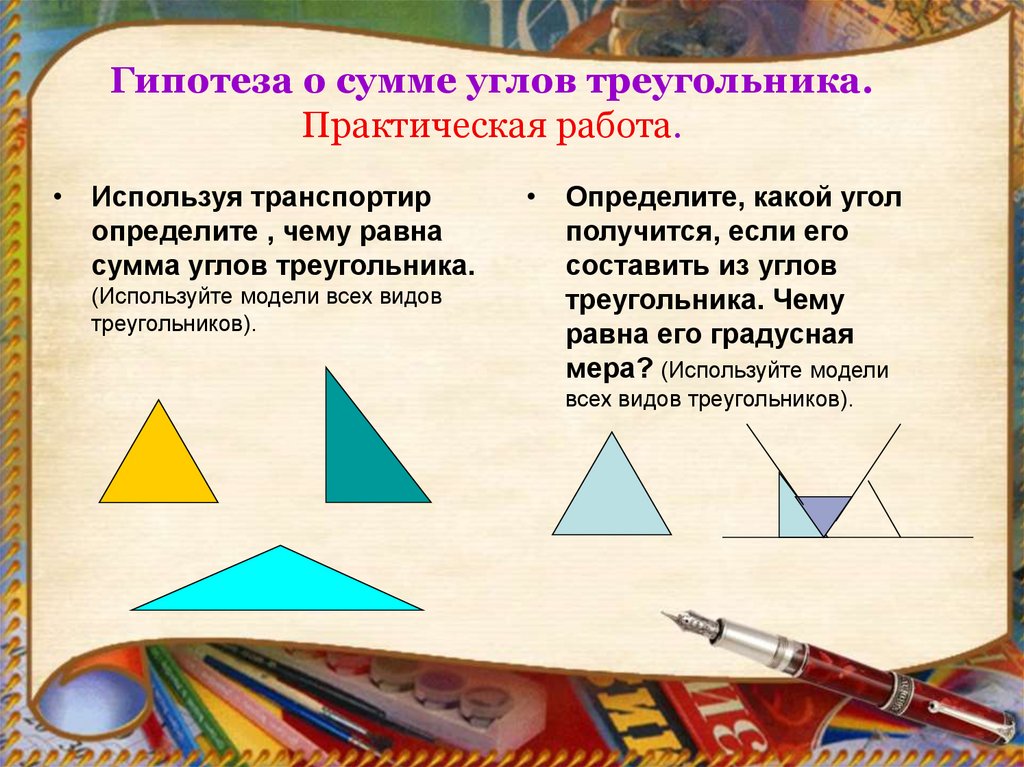
Гипотеза о сумме углов треугольника.Практическая работа.
• Используя транспортир
определите , чему равна
сумма углов треугольника.
(Используйте модели всех видов
треугольников).
• Определите, какой угол
получится, если его
составить из углов
треугольника. Чему
равна его градусная
мера? (Используйте модели
всех видов треугольников).
13. Выводы
I. Сумма углов треугольника равна 180˚.II. Углы треугольника вместе образуют
развернутый угол.
В О П Р О С Ы
Можно ли быть уверенным в том , что в
каждом треугольнике сумма углов равна
180˚?
2. Можно ли измерить углы любого
треугольника?
14. Выдающийся математик Д. Пойа.
«Если вы хотите научитьсяплавать, то смело
входите в воду,
а если хотите научиться
решать задачи,
то решайте их»
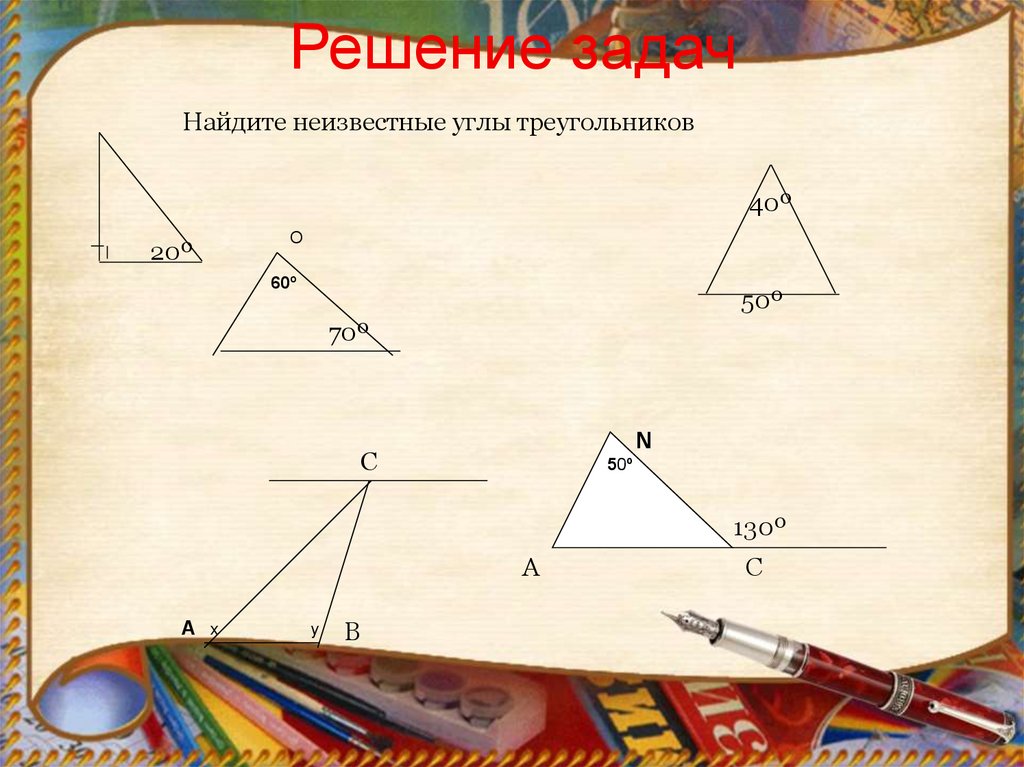
15. Решение задач
Найдите неизвестные углы треугольников40º
20º
О
60º
50º
70º
N
С
50º
130º
А
А х
у
В
С
16. Составьте пятистрочие: «Синквейн» (пятистрочие)
____________________________урок________________________( напишите одно существительное)
_______________________________________________________
(напишите два прилагательных, выражающих ассоциации
относительно понятия, обозначенного существительным)
______________________________________________________
(напишите три глагола)
________________________________________________________
(напишите предложение)
________________________________________________________
(напишите заключительное слово или фразу)
17. Домашнее задание.
• Изучить § 12 , решить № 157• Повторить доказательство теоремы











 mathematics
mathematics








