Аксиомы стереометрии

1.

Ч
ТО
ЗНАЧИТ
ЭТО
«Гео»-земля
СЛОВО?
«метрио»-меряю
Измеряю все что на Земле

2. Из каких разделов состоит геометрия?

• Планиметрия
?
«плано»
плоскость
• Стереометрия
?
«Stereos»
Телесный,
объемный,
пространственный

3. Что изучают эти разделы?

В чем отличие плоскостных
фигур
и пространственных
Что изучают
эти разделы?
тел?
• планиметрия
Плоскостные фигуры
Изучает
на плоскости
лежат вфигуры
одной плоскости
и имеют
два измерения
Какие
плоскостные
фигуры
вы знаете?
• стереометрия
Пространственные тела
Изучаетобъемные
фигуры в пространстве
и Какие
имеютпространственные
три измерения
фигуры
вы знаете?

4. Машиностроении

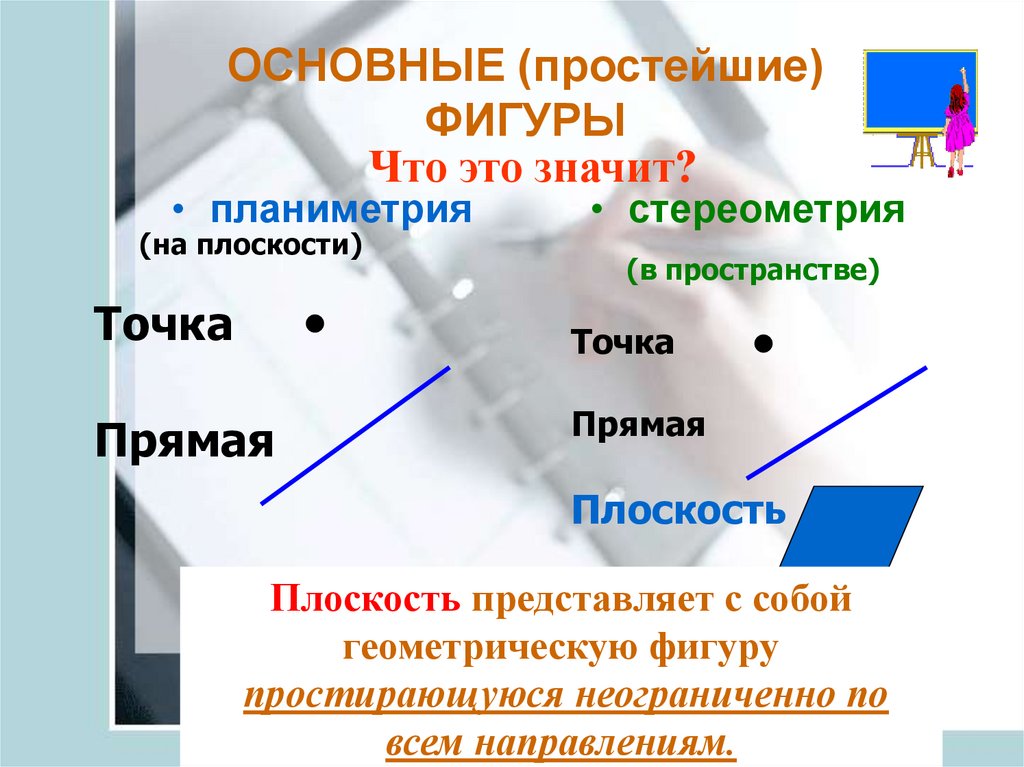
5. ОСНОВНЫЕ (простейшие) ФИГУРЫ

Что это значит?
• планиметрия
(на плоскости)
Точка
• стереометрия
(в пространстве)
Точка
Прямая
Прямая
Плоскость
Плоскость представляет с собой
геометрическую фигуру
простирающуюся неограниченно по
всем направлениям.

6.

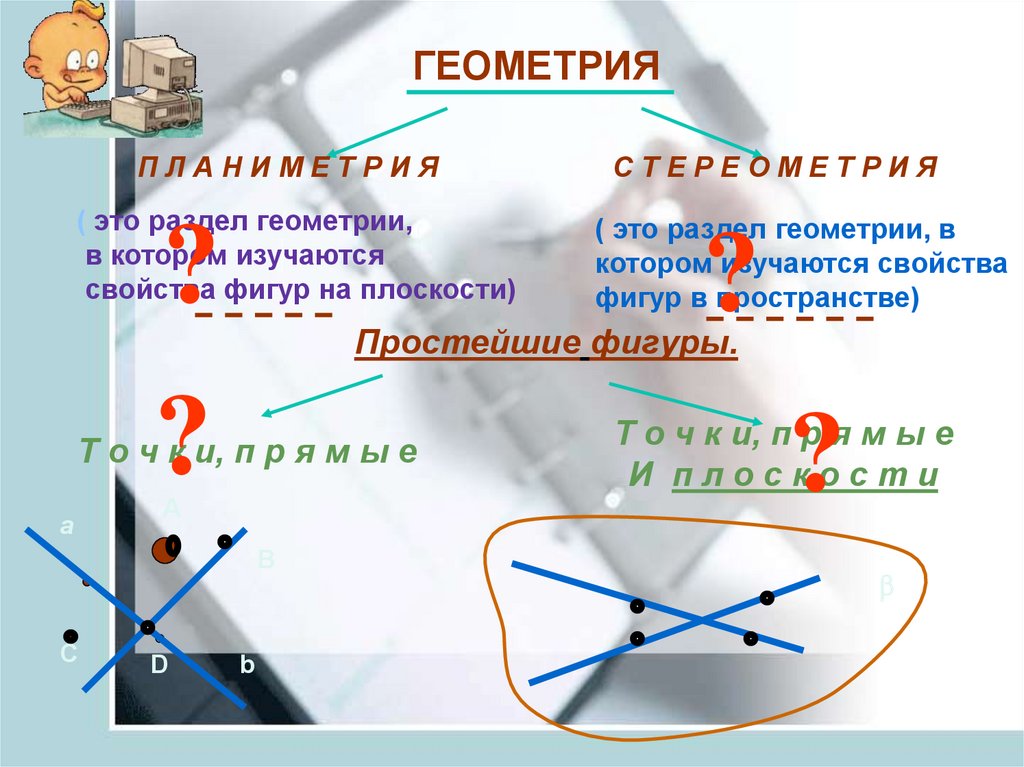
ГЕОМЕТРИЯ
ПЛАНИМЕТРИЯ
( это раздел геометрии,
в котором изучаются
свойства фигур на плоскости)
?
?
А
В
С
D
( это раздел геометрии, в
котором изучаются свойства
фигур в пространстве)
?
Простейшие фигуры.
Т о ч к и, п р я м ы е
a
СТЕРЕОМЕТРИЯ
b
?
Т о ч к и, п р я м ы е
И плоскости
b

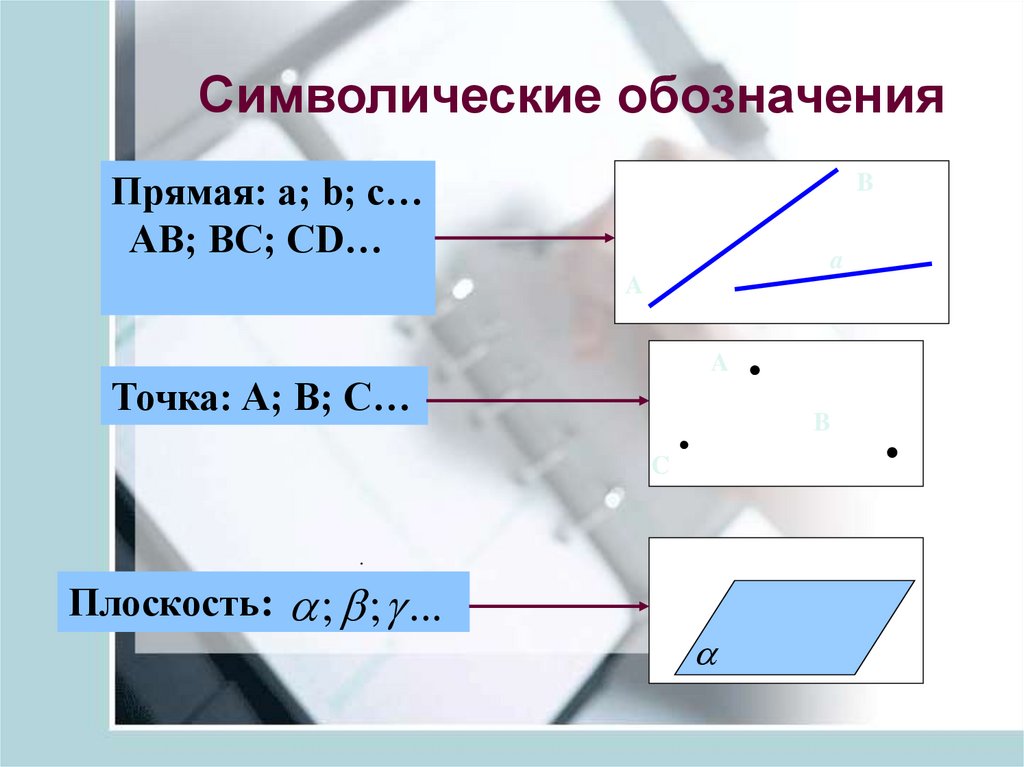
7. Символические обозначения

Прямая: a; b; c…
AB; BC; CD…
B
a
A
A
Точка: A; B; C…
C
B
Плоскость:
; b ; ...

8. Обозначения

Принадлежит, лежит
Не принадлежит, не лежит
пересекается
содержится

9. П р о ч т и ч е р т е ж

Прочти чертеж
С
А
A
C

10. П р о ч т и ч е р т е ж

a
а
b B
Прочти чертеж
С
c
b
B
С

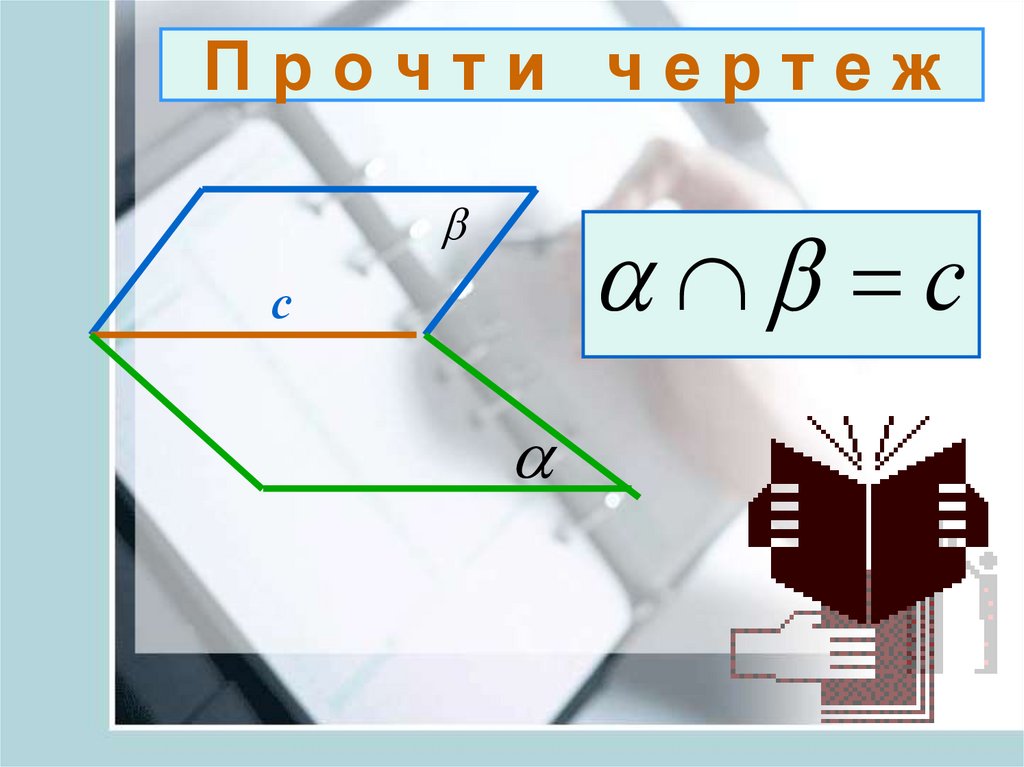
11. П р о ч т и ч е р т е ж

Прочти чертеж
b
b с
с

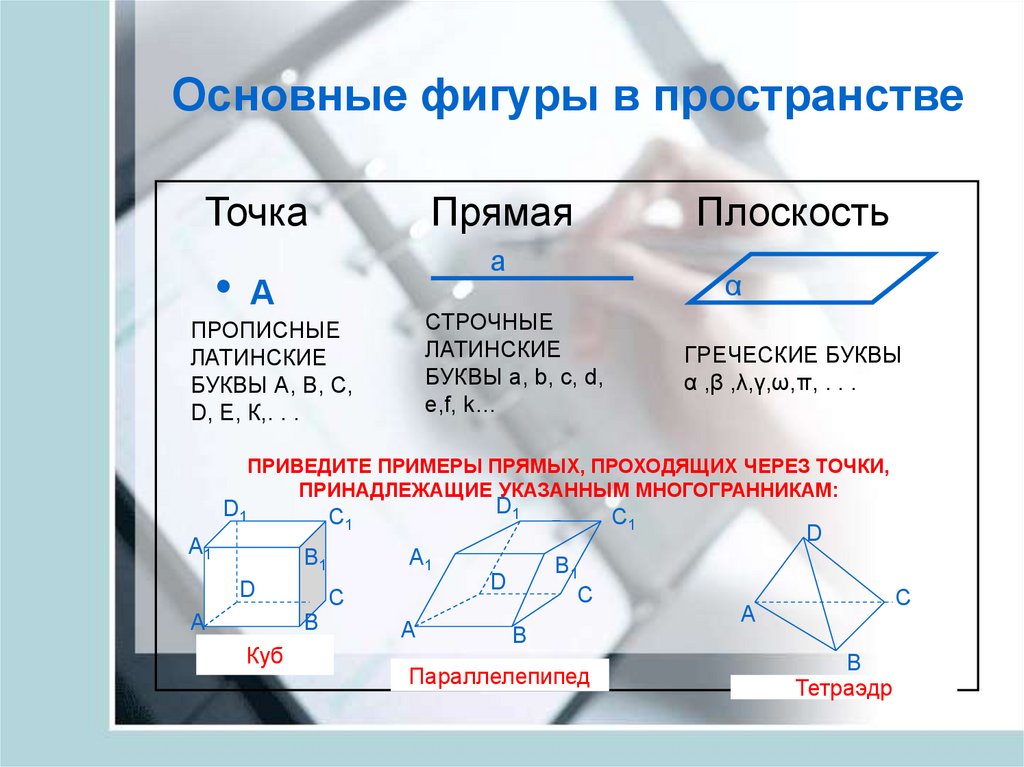
12. Основные фигуры в пространстве

Точка
Прямая
Плоскость
a
А
α
СТРОЧНЫЕ
ЛАТИНСКИЕ
БУКВЫ a, b, c, d,
e,f, k…
ПРОПИСНЫЕ
ЛАТИНСКИЕ
БУКВЫ А, В, С,
D, Е, К,. . .
ГРЕЧЕСКИЕ БУКВЫ
α ,β ,λ,γ,ω,π, . . .
ПРИВЕДИТЕ ПРИМЕРЫ ПРЯМЫХ, ПРОХОДЯЩИХ ЧЕРЕЗ ТОЧКИ,
ПРИНАДЛЕЖАЩИЕ УКАЗАННЫМ МНОГОГРАННИКАМ:
D1
А1
В1
D
А
В
Куб
D1
С1
А1
С
А
С1
В1
С
D
В
Параллелепипед
D
С
А
В
Тетраэдр

13. А к с и о м а

Аксиома
(от греч. “a x i ό m a” принимаемое
без доказательства)
Исходное положение
научной теории
принимаемое без
доказательства

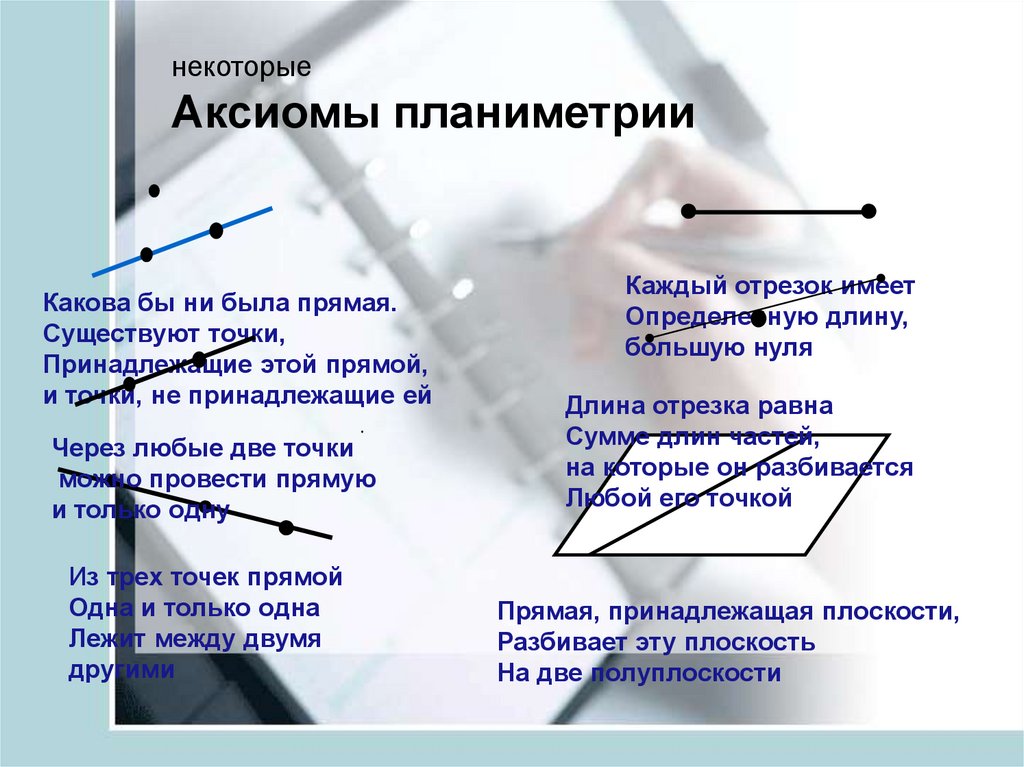
14. некоторые Аксиомы планиметрии

Какова бы ни была прямая.
Существуют точки,
Принадлежащие этой прямой,
и точки, не принадлежащие ей
Через любые две точки
можно провести прямую
и только одну
Из трех точек прямой
Одна и только одна
Лежит между двумя
другими
Каждый отрезок имеет
Определенную длину,
большую нуля
Длина отрезка равна
Сумме длин частей,
на которые он разбивается
Любой его точкой
Прямая, принадлежащая плоскости,
Разбивает эту плоскость
На две полуплоскости

15. Аксиома

С
А
A1
A
C
Какова бы ни была плоскость,
существуют точки,
принадлежащие этой плоскости,
и точки, не принадлежащие ей

16.

А1
А
К
С
И
О
М
А
1
A
C
B
А1. Через любые три точки,
не лежащие на одной прямой,
проходит плоскость,
и притом только одна

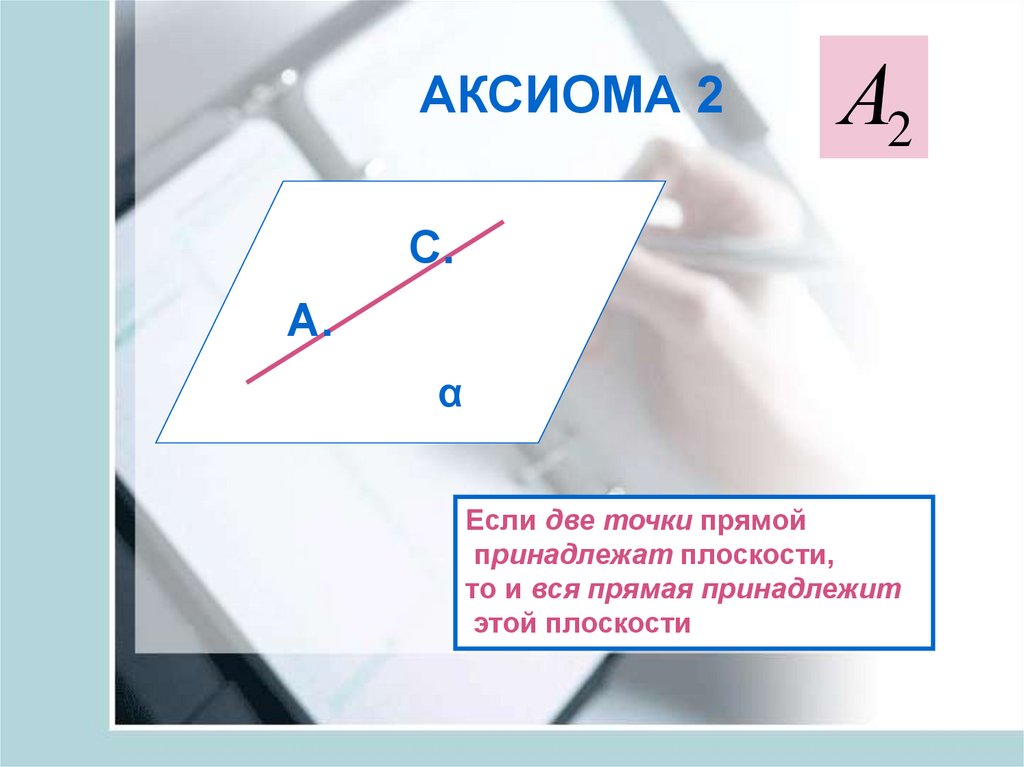
17. АКСИОМА 2

А2
С.
А.
α
Если две точки прямой
принадлежат плоскости,
то и вся прямая принадлежит
этой плоскости

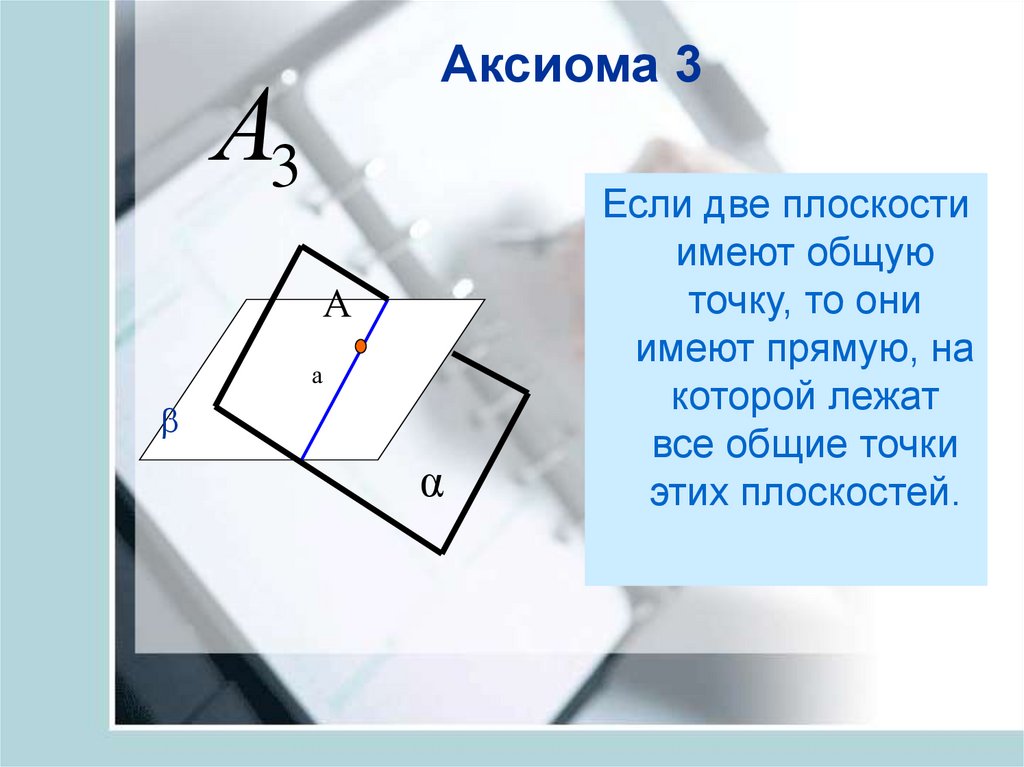
18. Аксиома 3

А3
А
а
b
α
Если две плоскости
имеют общую
точку, то они
имеют прямую, на
которой лежат
все общие точки
этих плоскостей.

19.

А3
А
а
b
α
• Точка, лежащая на линии пересечения
двух плоскостей, лежит на каждой из
этих плоскостей
• Точка, лежащая на двух каких-нибудь
плоскостях, лежит на линии
пересечения этих плоскостей

20. Аксиомы стереометрии Сформулируйте аксиомы А1, А2, А3. Прокомментируйте их с помощью приведенных рисунков.

В.
А.
α
С.
А, В,С – произвольные точки,
не лежащие на одной прямой.
Через точки А, В, С проходит
единственная плоскость α.
А.
В.
С.
α
А , В ,
С АВ
С
β
а
А.
α
А , А b
b а, А а

21.

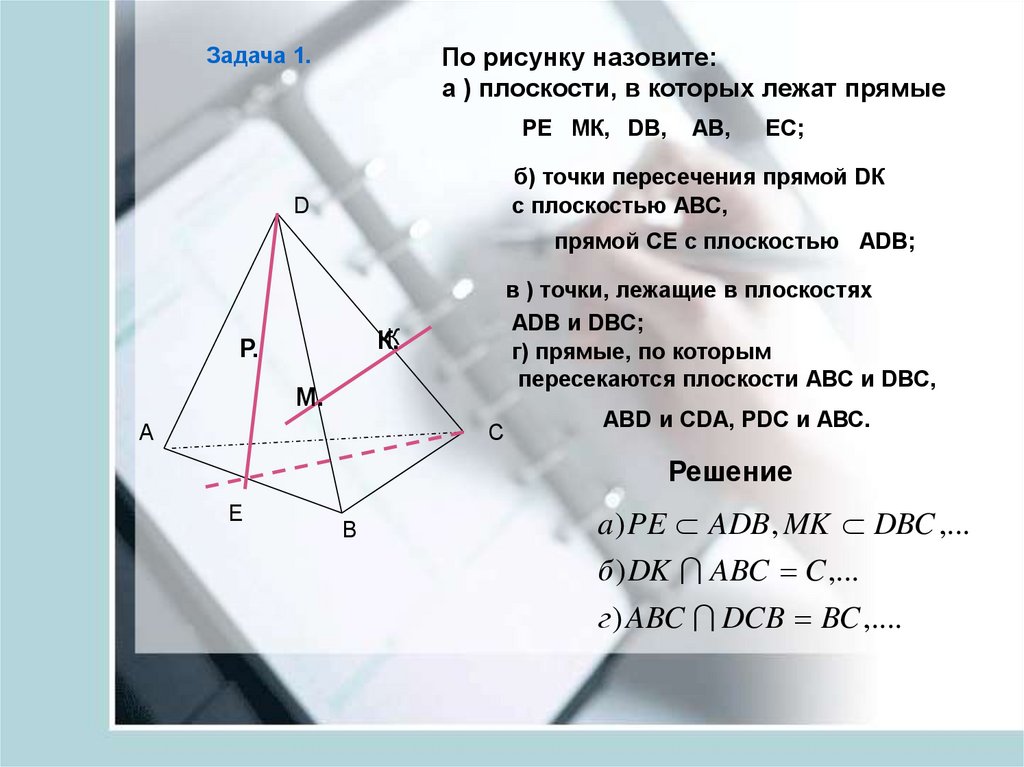
Задача 1.
По рисунку назовите:
a ) плоскости, в которых лежат прямые
РЕ МК, DВ,
АВ,
ЕС;
б) точки пересечения прямой DК
с плоскостью АВС,
D
прямой СЕ с плоскостью АDВ;
в ) точки, лежащие в плоскостях
АDВ и DВС;
г) прямые, по которым
пересекаются плоскости АВС и DВС,
К
К.
Р.
М.
А
С
АВD и СDА, РDС и АВС.
Решение
Е
В
a ) PE ADB , MK DBC ,...
б ) DK ABC C ,...
г ) ABC DCB BC ,....

22. Литература

• http://www.photosight.ru
• http://www.college.ru/mathematics/courses/.html
• Учебник. Геометрия для 10-11 классов
общеобразовательных учреждений. Москва
«Просвещение» 7-е издание 1999 г.Авторы.
Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев,
Л.С.Киселева, Э.Г.Поздняк.
• Книга для учителя. С.М.Саакян, В.Ф.Бутузов.
Изучение геометрии в 10-11 классе.
Методические рекомендации к учебнику.
Москва «Просвещение» 2001г.