Similar presentations:
Аксиомы стереометрии
1.
Аксиомы стереометрии«Старайтесь, прежде чем
приступить к выполнению
любого задания на уроке или
дома, чётко определить
вид своей деятельности»
2
2. Аксиомы стереометрии
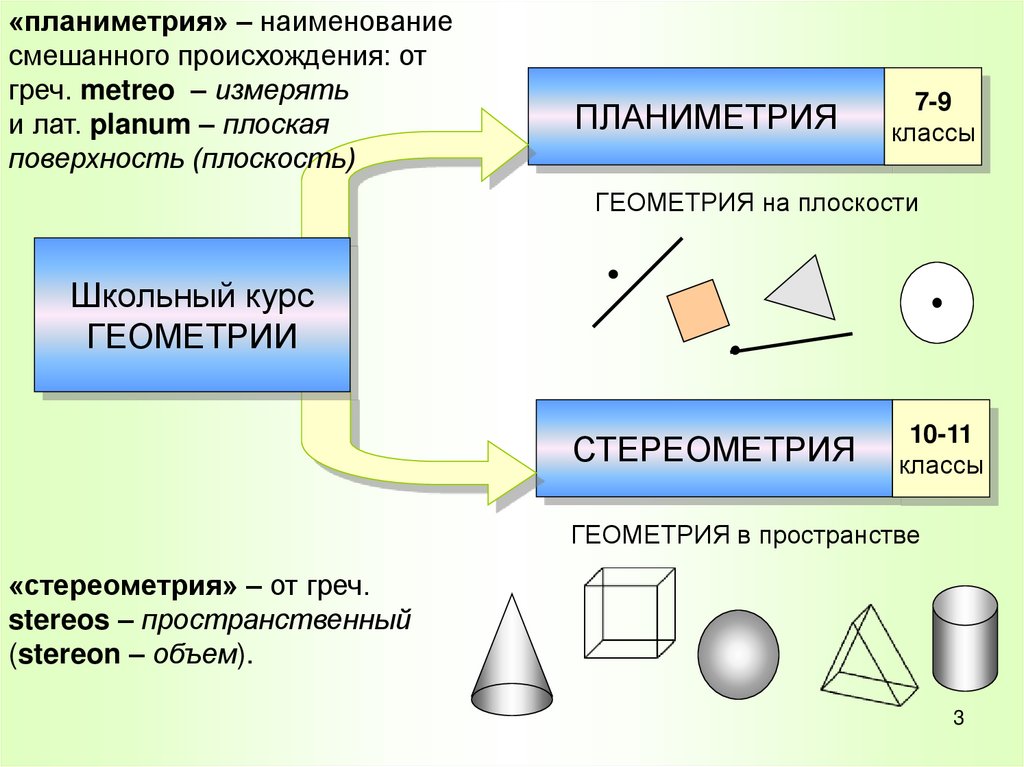
«планиметрия» – наименованиесмешанного происхождения: от
греч. metreo – измерять
и лат. planum – плоская
поверхность (плоскость)
ПЛАНИМЕТРИЯ
7-9
классы
ГЕОМЕТРИЯ на плоскости
Школьный курс
ГЕОМЕТРИИ
СТЕРЕОМЕТРИЯ
10-11
классы
ГЕОМЕТРИЯ в пространстве
«стереометрия» – от греч.
stereos – пространственный
(stereon – объем).
3
3.
Мы знаем,что
Геометрия возникла из
практических задач людей;
Геометрия лежит в основе
всей техники и большинства
изобретений человечества;
Геометрия нужна
- технику
- инженеру
- рабочему
- архитектору
- модельеру …
4
4.
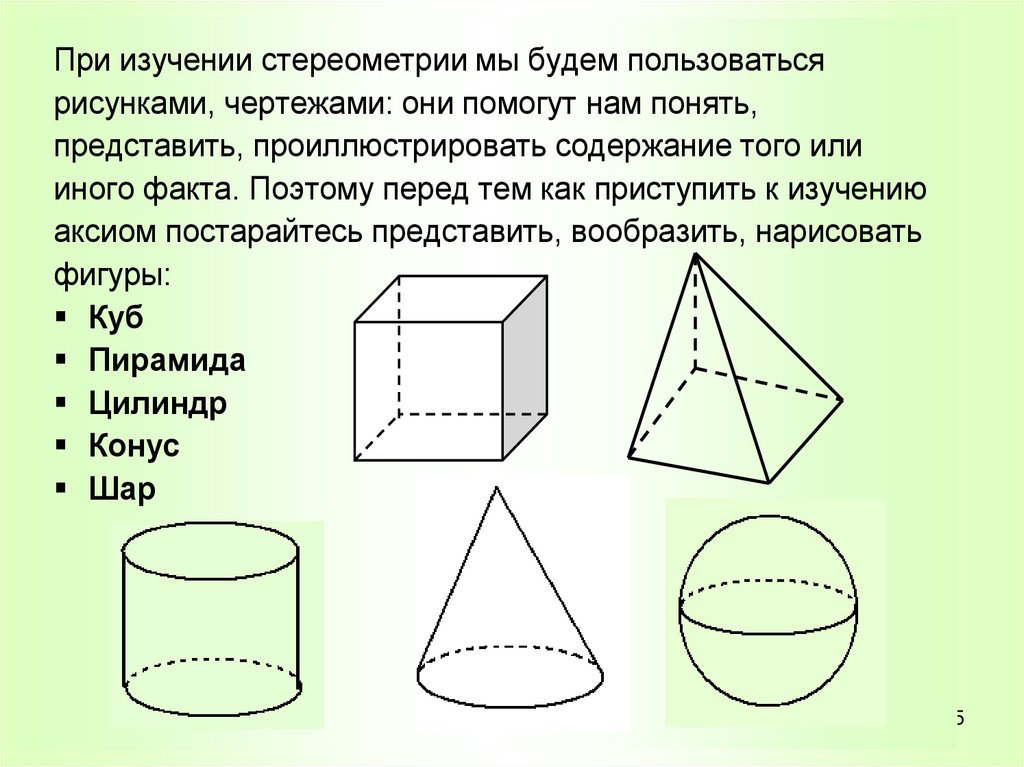
При изучении стереометрии мы будем пользоватьсярисунками, чертежами: они помогут нам понять,
представить, проиллюстрировать содержание того или
иного факта. Поэтому перед тем как приступить к изучению
аксиом постарайтесь представить, вообразить, нарисовать
фигуры:
Куб
Пирамида
Цилиндр
Конус
Шар
5
5.
Логическое строение геометрии:1. Основные геометрические понятия
2. Аксиомы
3. Определения
4. Теоремы
6
6.
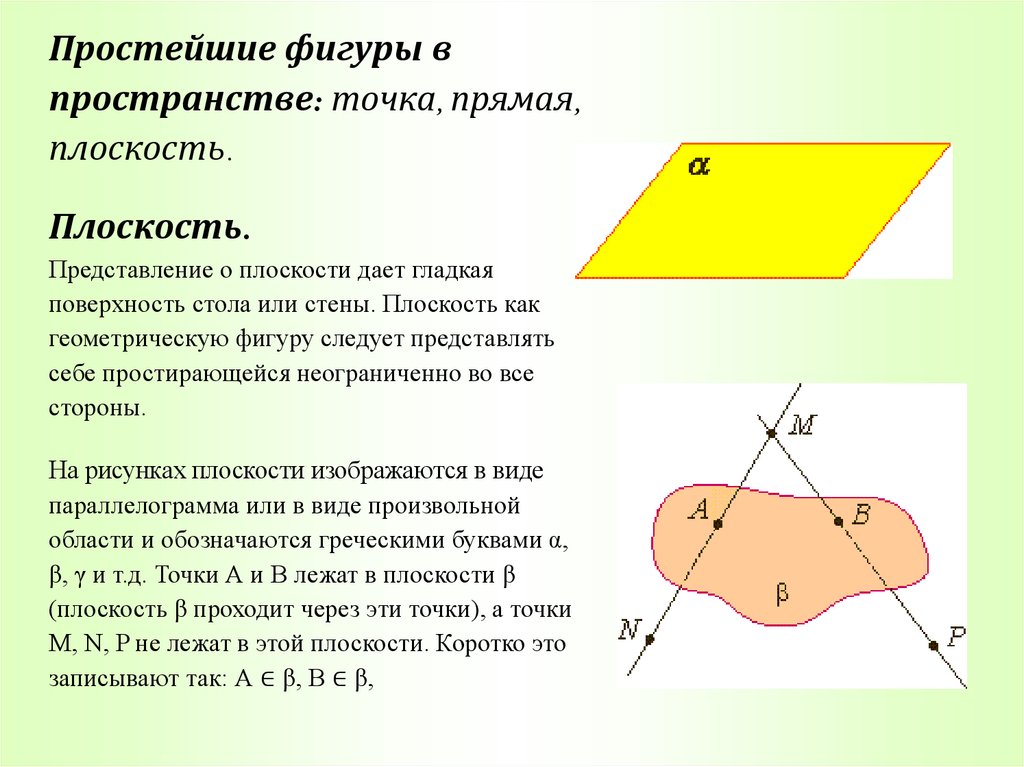
Простейшие фигуры впространстве: точка, прямая,
плоскость.
Плоскость.
Представление о плоскости дает гладкая
поверхность стола или стены. Плоскость как
геометрическую фигуру следует представлять
себе простирающейся неограниченно во все
стороны.
На рисунках плоскости изображаются в виде
параллелограмма или в виде произвольной
области и обозначаются греческими буквами α,
β, γ и т.д. Точки А и В лежат в плоскости β
(плоскость β проходит через эти точки), а точки
M, N, P не лежат в этой плоскости. Коротко это
записывают так: А ∈ β, B ∈ β,
7.
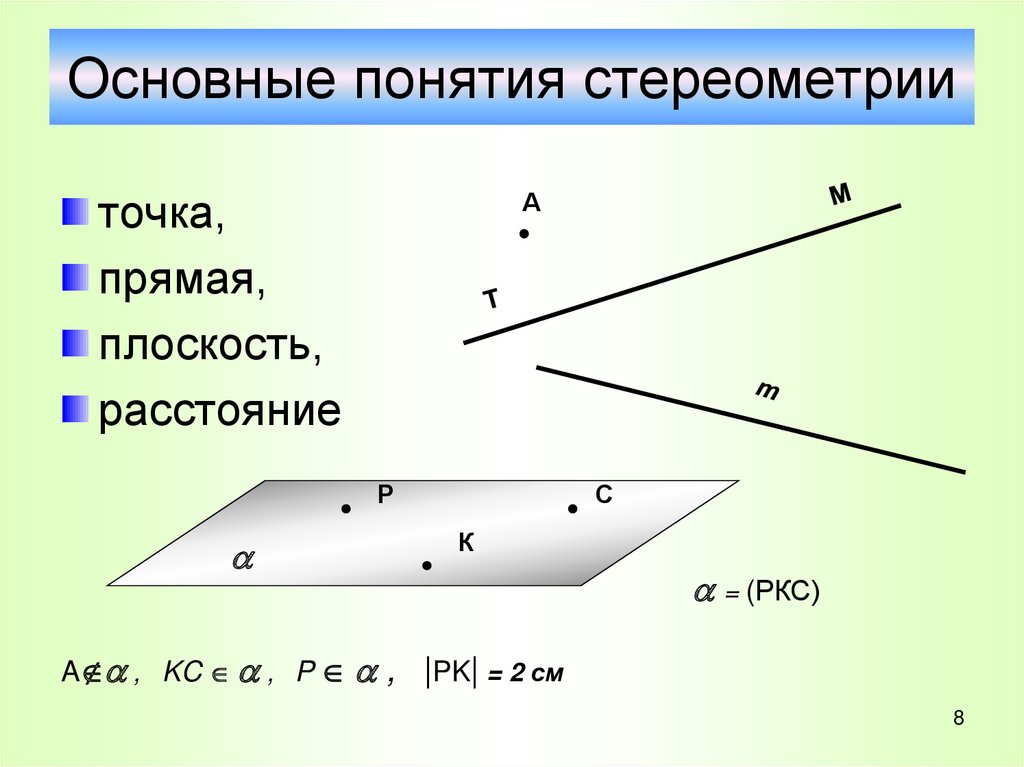
Основные понятия стереометрииточка,
прямая,
плоскость,
расстояние
А
Р
A , KC , P
С
К
= (РКС)
, |PK| = 2 см
8
8. Основные понятия стереометрии
Аксиомы стереометрииСлово «аксиома» греческого происхождения и в переводе означает
истинное, исходное положение теории.
Система аксиом стереометрии дает описание
свойств пространства и основных его элементов
Понятия «точка», «прямая», «плоскость», «расстояние»
принимаются без определений: их описание и свойства содержатся в
аксимах
9
9. Аксиомы стереометрии
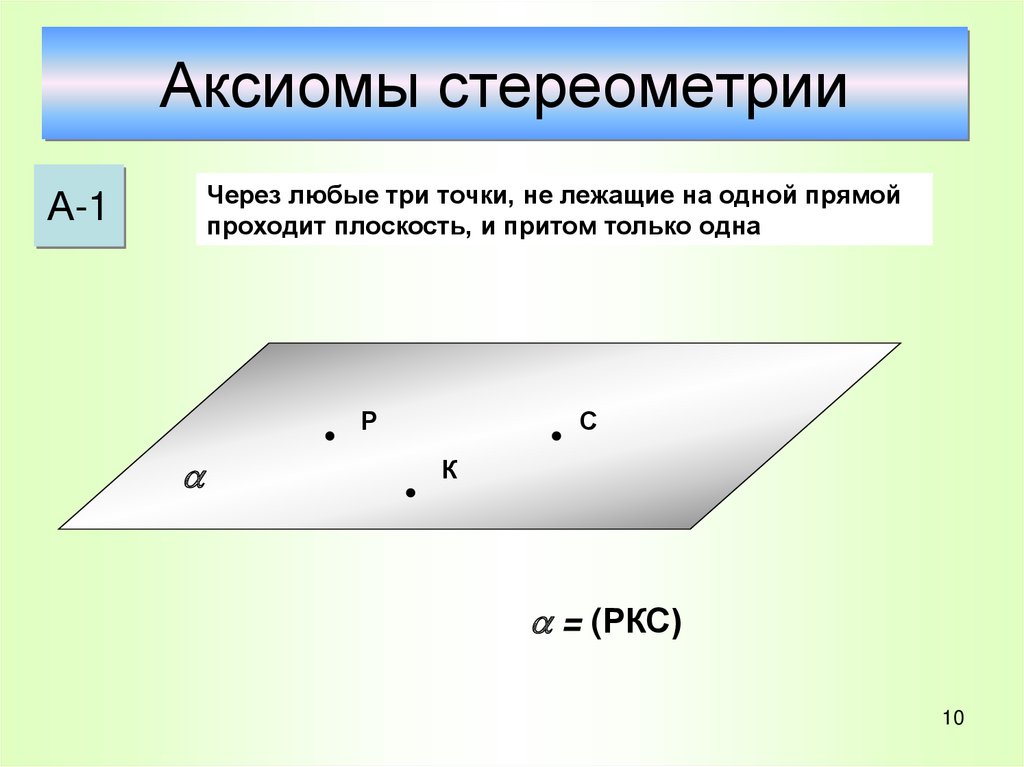
Через любые три точки, не лежащие на одной прямойпроходит плоскость, и притом только одна
А-1
Р
С
К
= (РКС)
10
10. Аксиомы стереометрии
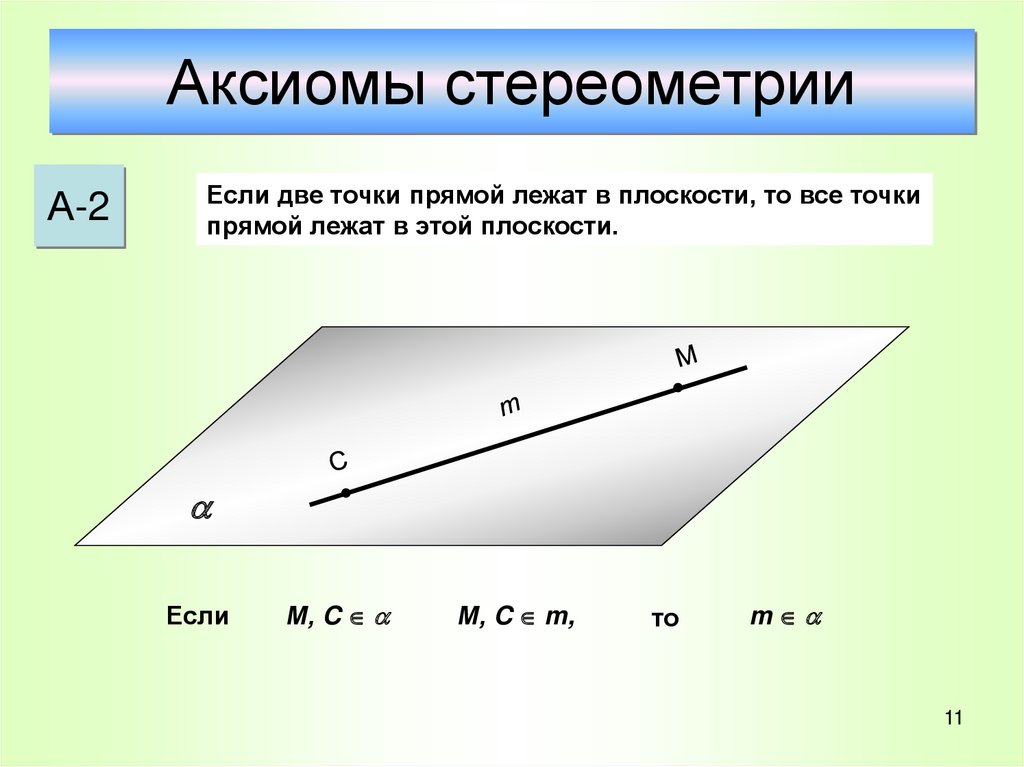
А-2Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Если
М, C
М, C m,
то
m
11
11. Аксиомы стереометрии
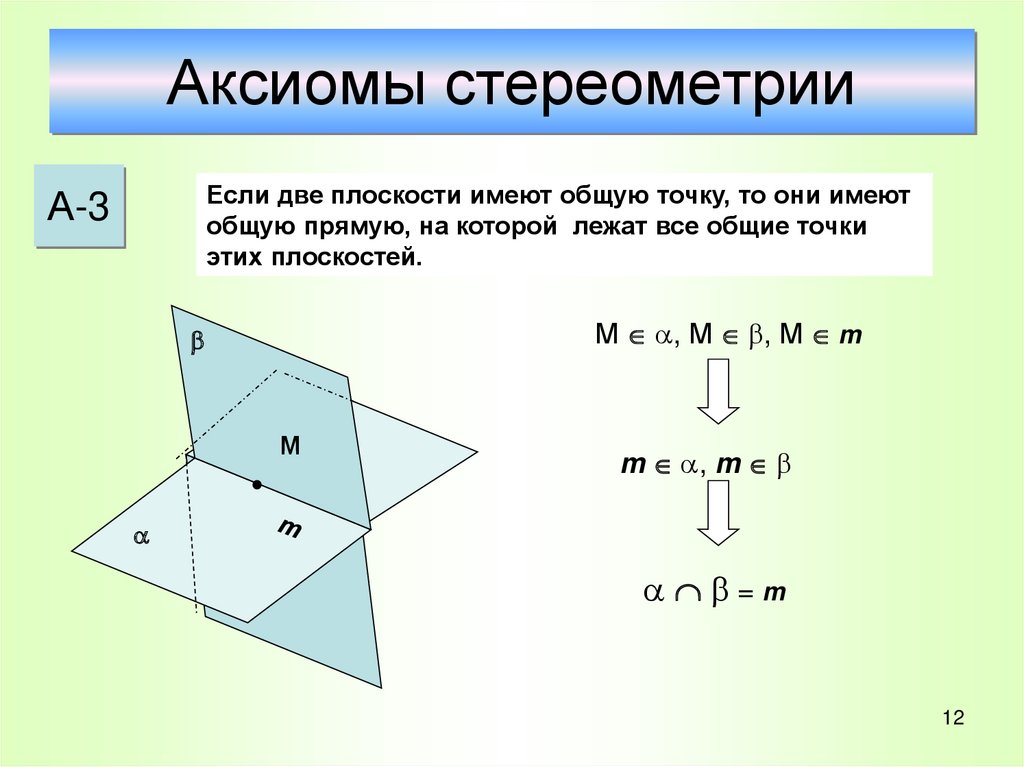
Если две плоскости имеют общую точку, то они имеютобщую прямую, на которой лежат все общие точки
этих плоскостей.
А-3
М , М , М m
М
m , m
=m
12
12. Аксиомы стереометрии
СЛЕДСТВИЯ ИЗ АКСИОМТ-1
Через любую прямую и не
принадлежащую ей точку можно
провести плоскость, и притом
только одну.
м
13
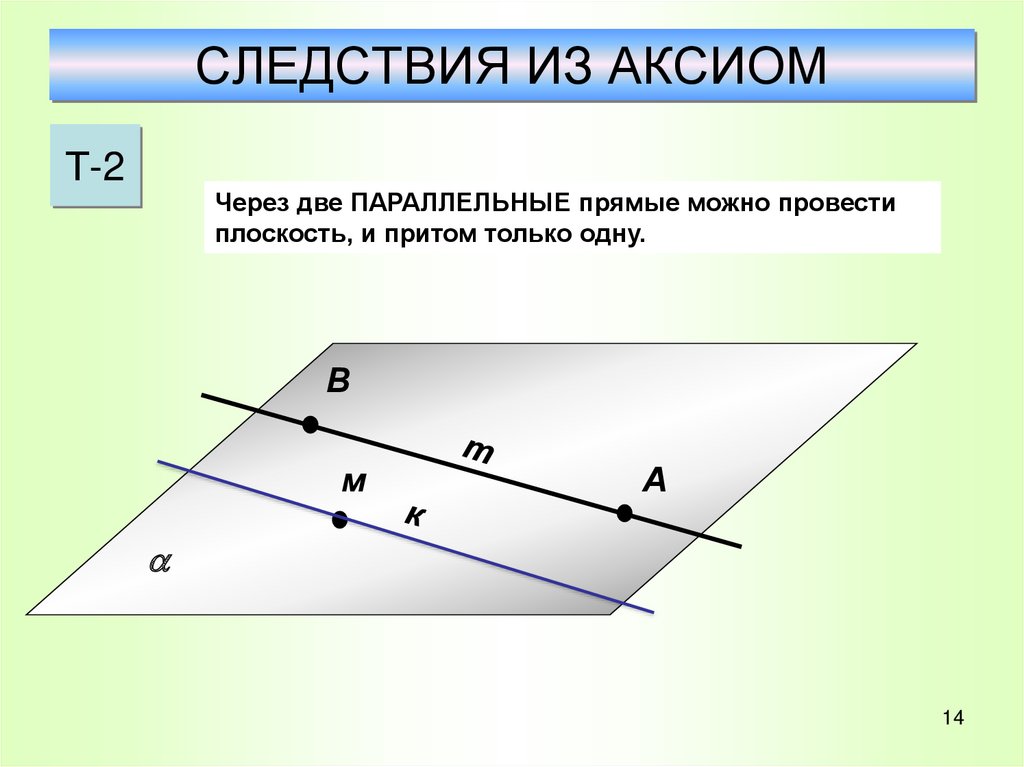
13. СЛЕДСТВИЯ ИЗ АКСИОМ
Т-2Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести
плоскость, и притом только одну.
В
м
А
14
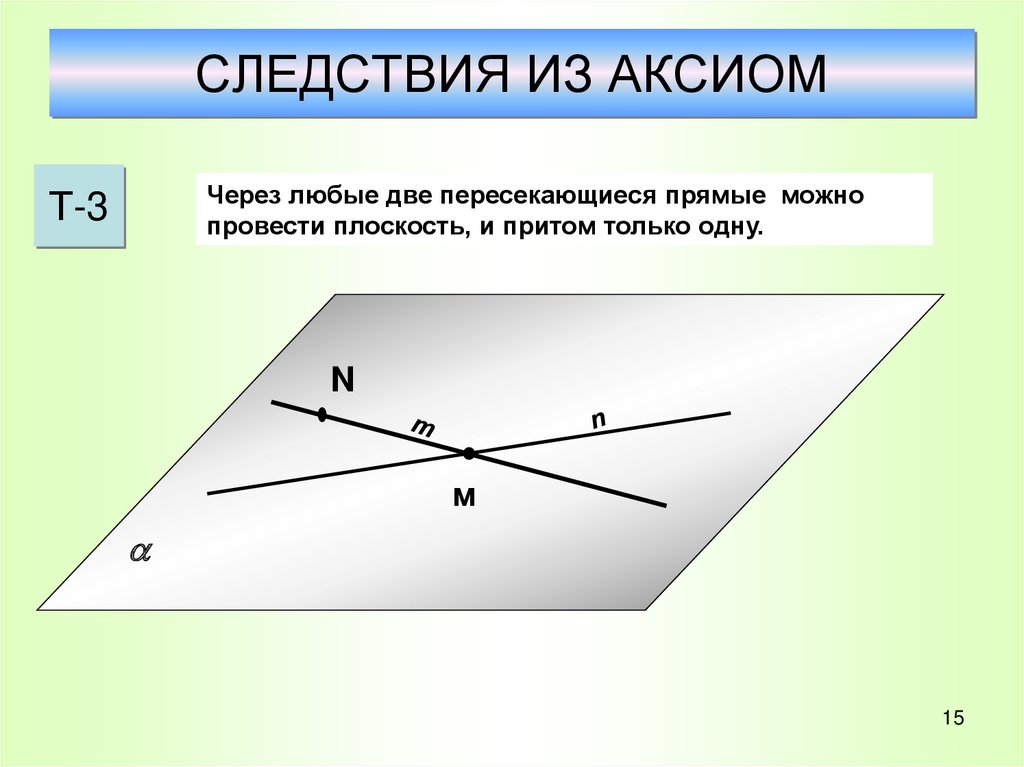
14. СЛЕДСТВИЯ ИЗ АКСИОМ
Через любые две пересекающиеся прямые можнопровести плоскость, и притом только одну.
Т-3
N
м
15
15. СЛЕДСТВИЯ ИЗ АКСИОМ
1616. Опорный конспект
Задание № 1Как в пространстве можно однозначно задать
плоскость?
По трем точкам, не лежащим на одной прямой
По прямой и точке, не лежащей на этой прямой
По двум пересекающимся прямым
По двум параллельным прямым
19
17. Аксиомы стереометрии
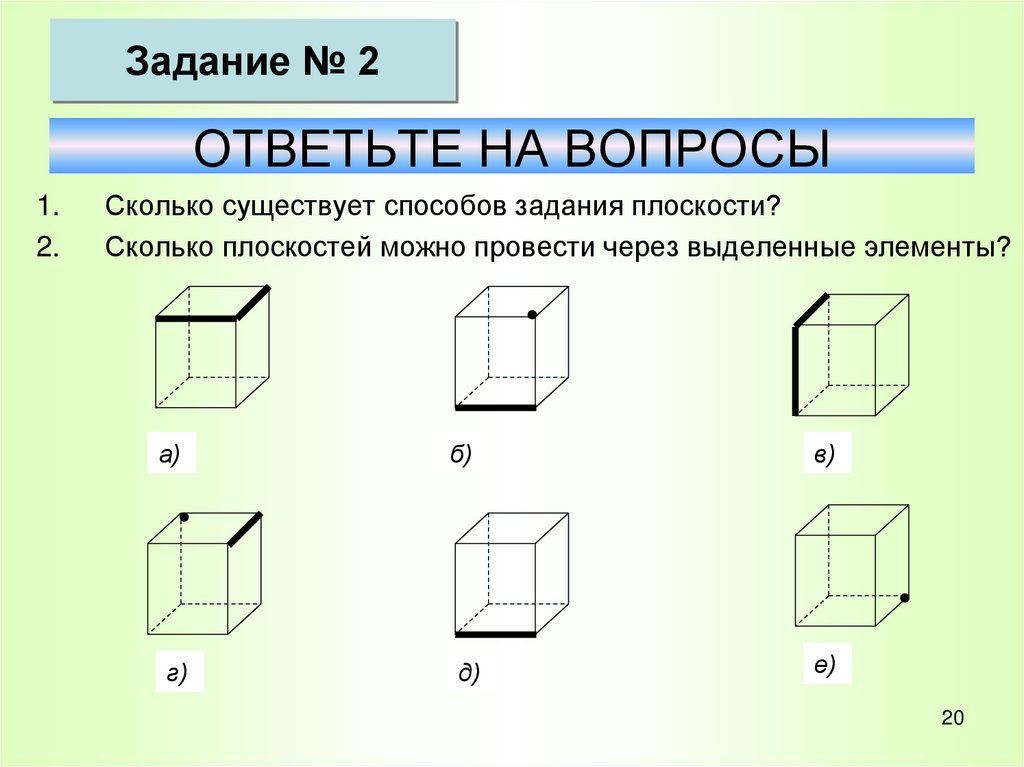
Задание № 2ОТВЕТЬТЕ НА ВОПРОСЫ
1.
2.
Сколько существует способов задания плоскости?
Сколько плоскостей можно провести через выделенные элементы?
а)
г)
б)
д)
в)
е)
20
18. Следствия из аксиом стереометрии
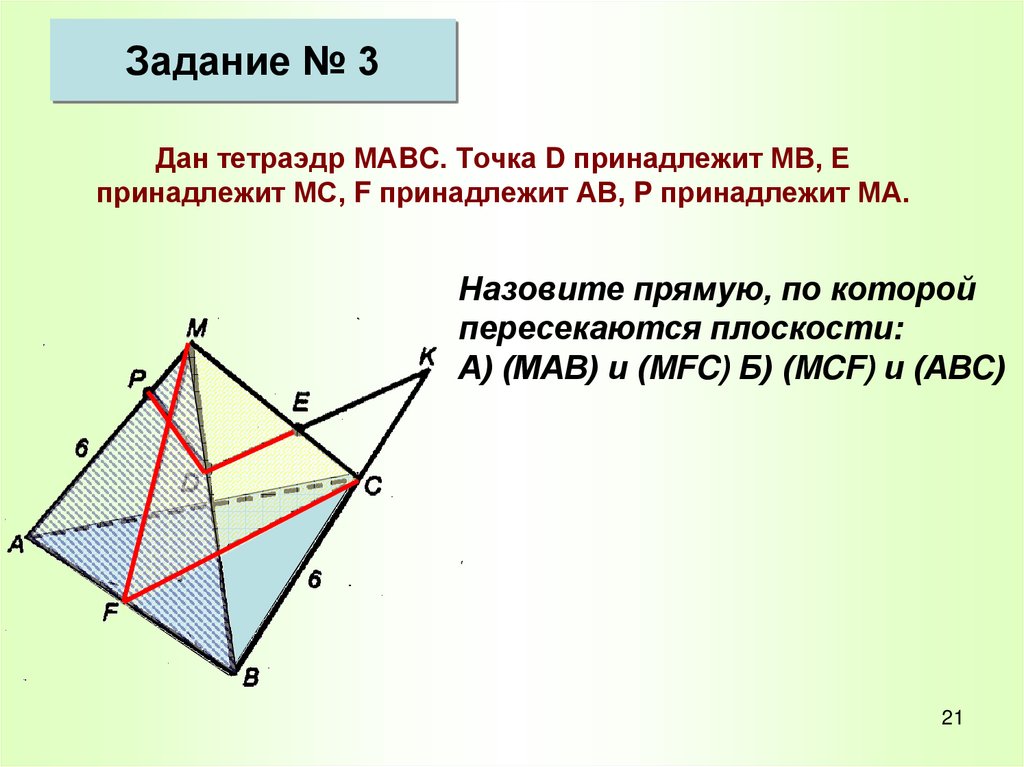
Задание № 3Дан тетраэдр МАBC. Точка D принадлежит МВ, Е
принадлежит МС, F принадлежит АВ, P принадлежит МА.
Назовите прямую, по которой
пересекаются плоскости:
А) (МАВ) и (MFC) Б) (MCF) и (АВС)
21
19. Как в пространстве можно однозначно задать плоскость?
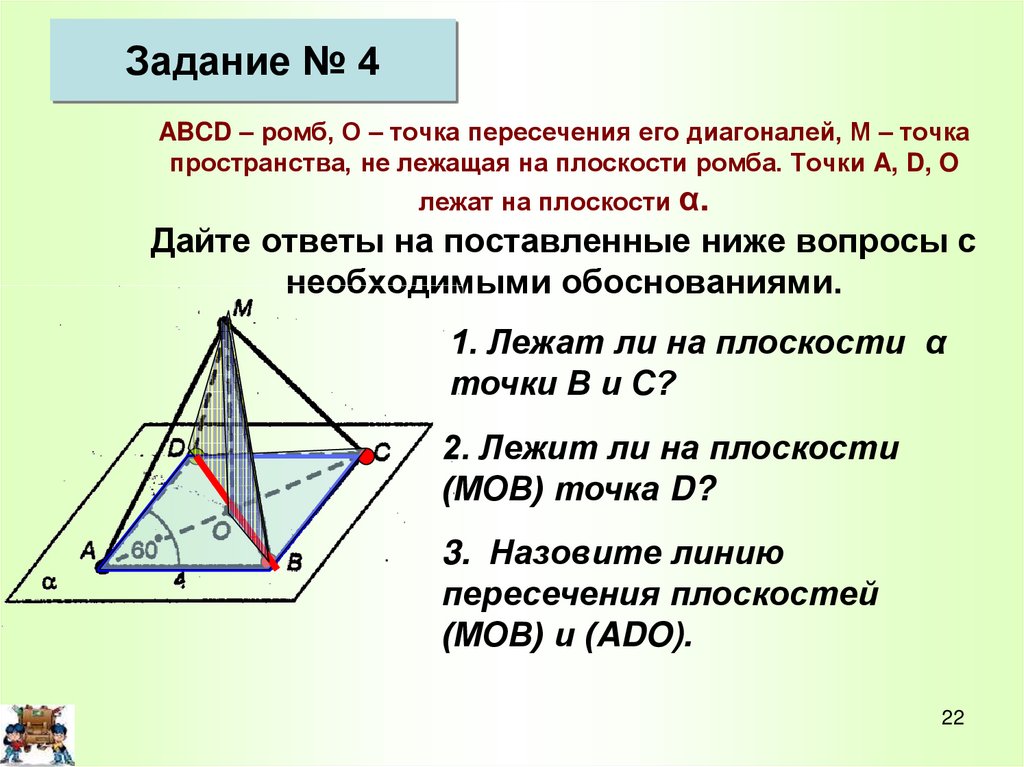
Задание № 4ABCD – ромб, О – точка пересечения его диагоналей, М – точка
пространства, не лежащая на плоскости ромба. Точки A, D, O
α.
Дайте ответы на поставленные ниже вопросы с
необходимыми обоснованиями.
лежат на плоскости
1. Лежат ли на плоскости α
точки В и С?
2. Лежит ли на плоскости
(МОВ) точка D?
3. Назовите линию
пересечения плоскостей
(МОВ) и (ADO).
22
20. ОТВЕТЬТЕ НА ВОПРОСЫ
Задание № 5Определите: верно, ли суждение? Дайте ответ «да» или «нет» и
почему?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Любые три точки лежат в одной плоскости.
Любые четыре точки лежат в одной плоскости.
Любые четыре точки не лежат в одной плоскости.
Через любые три точки проходит плоскость и при том только
одна.
Если прямая пересекает 2 стороны треугольника, то она
лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то она
лежит в плоскости треугольника.
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны.
Могут ли прямая и плоскость иметь только две общие точки?
Можно ли через точку пересечения двух прямых провести
третью прямую, не лежащую с ними в одной плоскости?
23







 mathematics
mathematics








