Similar presentations:
Аксиомы стереометрии
1. АКСИОМЫ СТЕРЕОМЕТРИИ
2.
• Стереометрия – это раздел геометрии, вкотором изучаются фигуры в пространстве.
• В стереометрии, также как и в планиметрии,
свойства геометрических фигур
устанавливаются путём доказательства
соответствующих теорем.
• При этом отправными являются свойства
основных геометрических фигур,
сформулированных в виде аксиом.
3.
Аксиомы – это первоначальные фактыгеометрии, которые принимаются без
доказательств и позволяют вывести из них
дальнейшие факты этой науки.
«Аксиомы обладают наивысшей степенью
общности и представляют начала всего»
АРИСТОТЕЛЬ
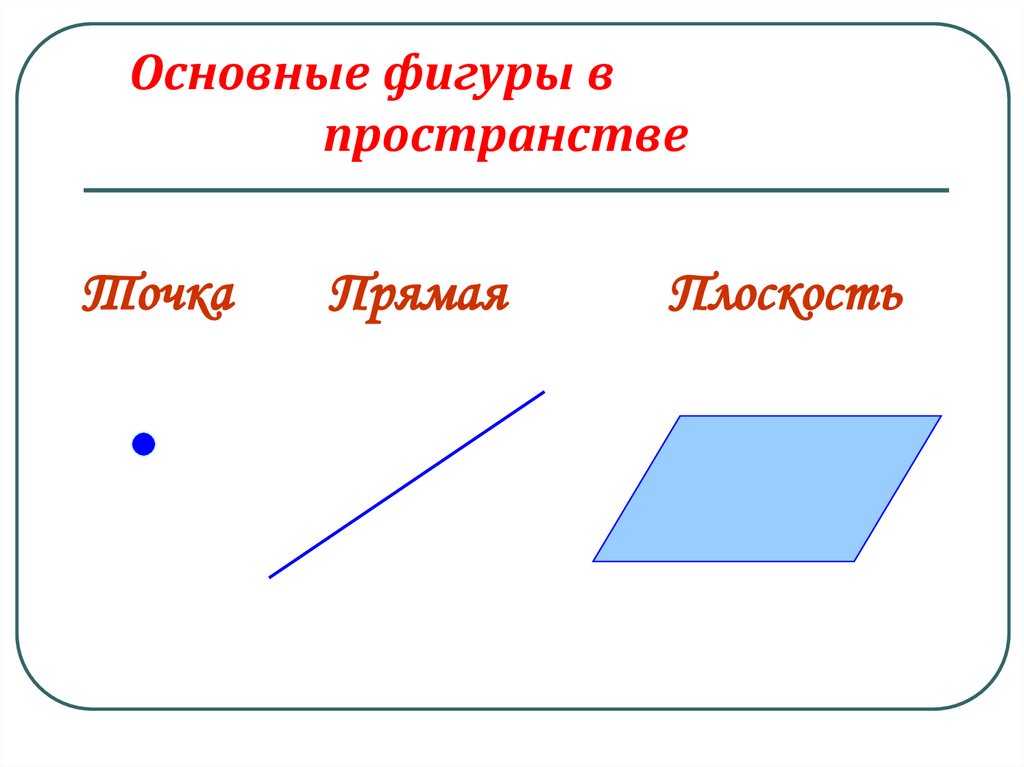
4. Основные фигуры в пространстве
ТочкаПрямая
Плоскость
5.
Изображать плоскость мы будем ввиде параллелограмма
или в виде произвольной области.
Плоскость, как и прямая, бесконечна. На рисунке мы
изображаем только часть плоскости, но
представляем её
неограниченно продолженной во все стороны
, , .,...
Плоскости обозначают греческими буквами
6.
Введение нового геометрическогообраза (плоскости) заставляет
расширить известную нам в
планиметрии систему аксиом.
Поэтому вводится группа
аксиом С, которая выражает
основные свойства плоскости в
пространстве. Эта группа
состоит из трёх аксиом.
7. Аксиомы группы С.
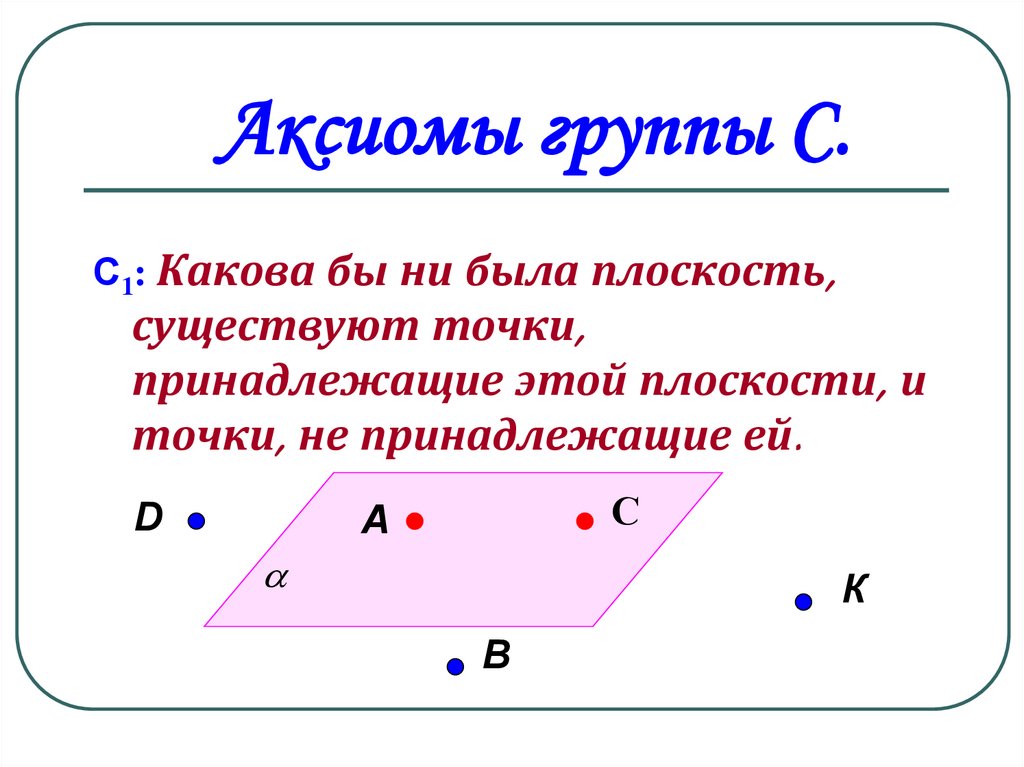
С1: Какова бы ни была плоскость,существуют точки,
принадлежащие этой плоскости, и
точки, не принадлежащие ей.
С
А
D
К
B
8. Аксиомы группы С.
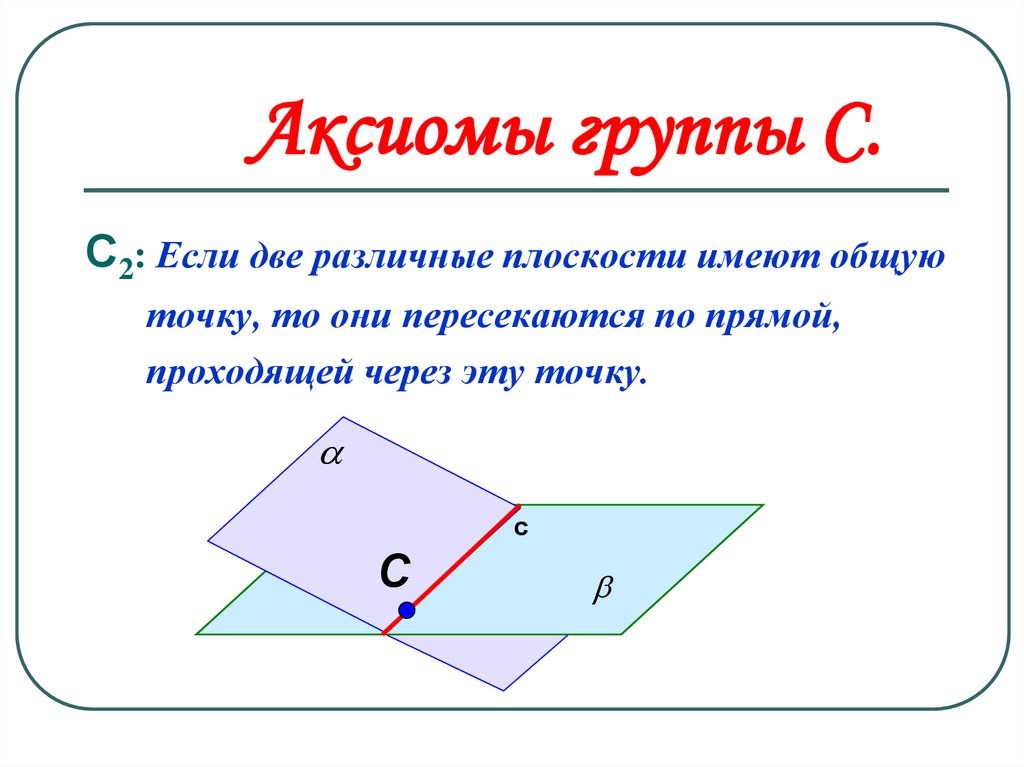
С2: Если две различные плоскости имеют общуюточку, то они пересекаются по прямой,
проходящей через эту точку.
с
С
9. Аксиомы группы С.
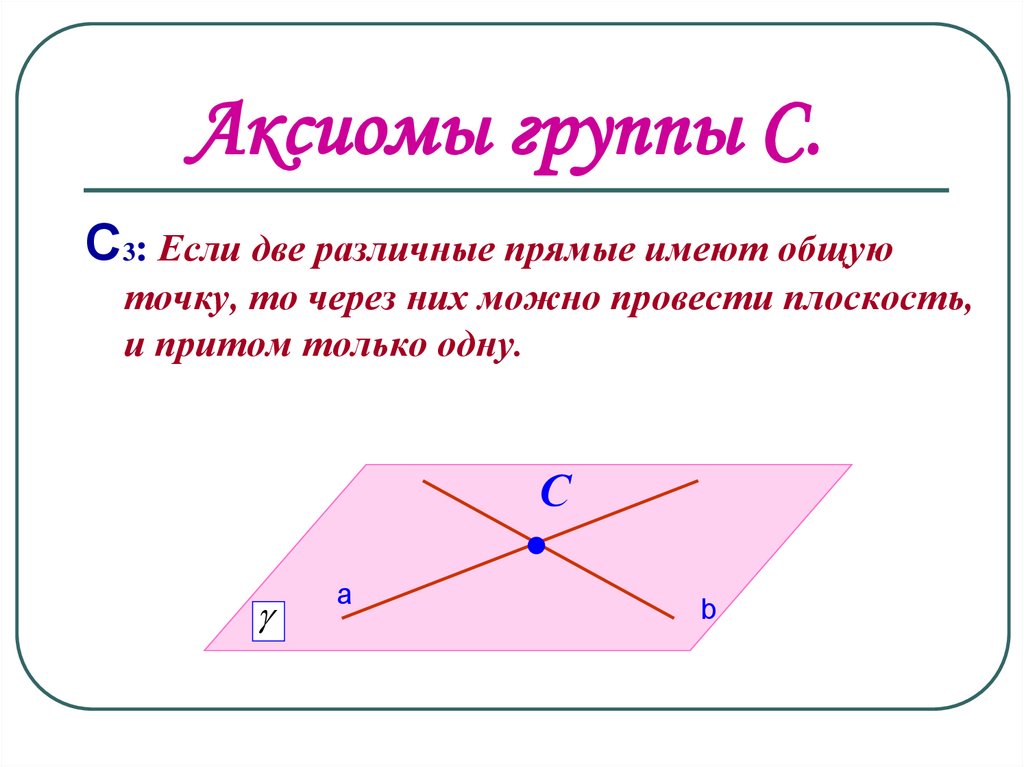
С3: Если две различные прямые имеют общуюточку, то через них можно провести плоскость,
и притом только одну.
С
a
b
10.
Аксиомы выражают интуитивноясные свойства плоскостей, их связь с
двумя другими основными фигурами
стереометрии – с прямыми и точками.
Рассмотренные аксиомы С1 - С3
относятся только к плоскостям, и к ним
необходимо добавить аксиомы о прямых,
аналогичные соответствующим
планиметрическим аксиомам.
Таким образом, система аксиом
стереометрии состоит из аксиом
планиметрии и аксиом группы С.
11. Система аксиом стереометрии
I1: Какова бы ни была прямая, существуют точки,принадлежащие этой прямой, и точки, не
принадлежащие ей.
I2 : Через любые две точки можно провести прямую, и
только одну.
12. Система аксиом стереометрии
II: Из трёх точек на прямой одна и только одна лежитмежду двумя другими.
III: Каждый отрезок имеет определённую длину,
большую нуля. Длина отрезка равна сумме длин
частей, на которые он разбивается любой его точкой.
С
А
АВ > 0
В
АВ = АС + СВ
13. Система аксиом стереометрии
IV: Прямая принадлежащая плоскости, разбивает этуплоскость на две полуплоскости.
14. Система аксиом стереометрии
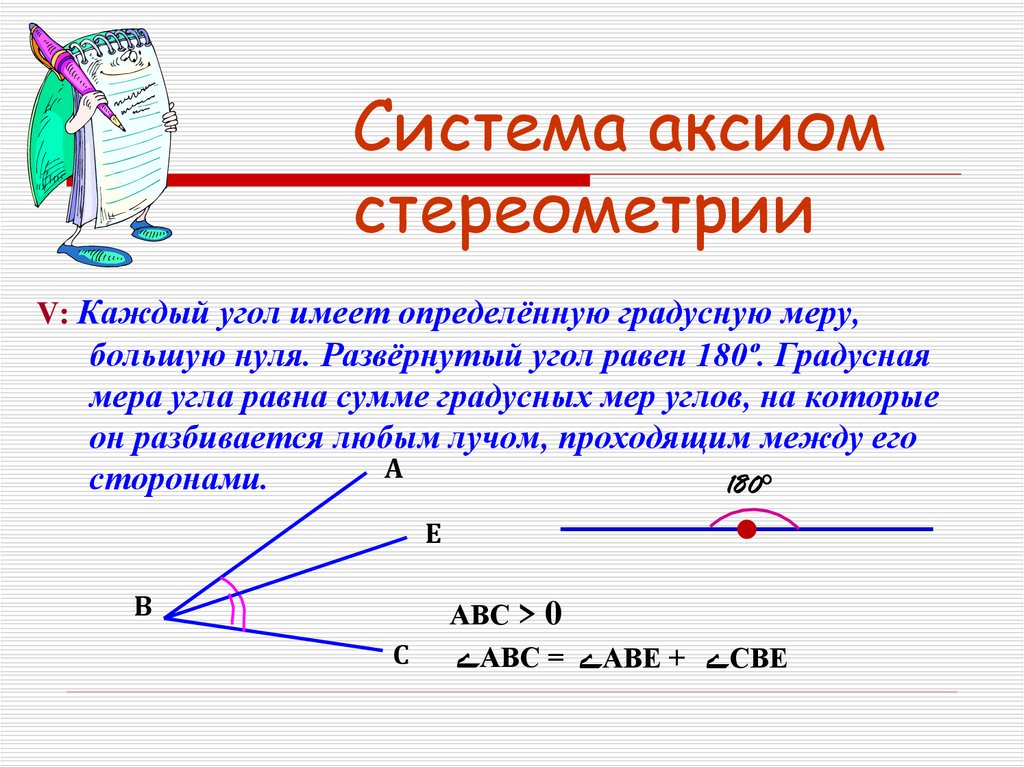
V: Каждый угол имеет определённую градусную меру,большую нуля. Развёрнутый угол равен 180º. Градусная
мера угла равна сумме градусных мер углов, на которые
он разбивается любым лучом, проходящим между его
А
сторонами.
180°
Е
В
С
АВС > 0
ےАВС = ےАВЕ + ےСВЕ
15. Система аксиом стереометрии
VI: На любой полупрямой от её начальной точкиможно отложить отрезок заданной длины, и
только один.
VII: От полупрямой на содержащей её плоскости в
заданную полуплоскость можно отложить угол с
заданной градусной мерой, меньшей 180º, и только
один.
О
а
ОК = а
К
К
А
О
А
16. Система аксиом стереометрии
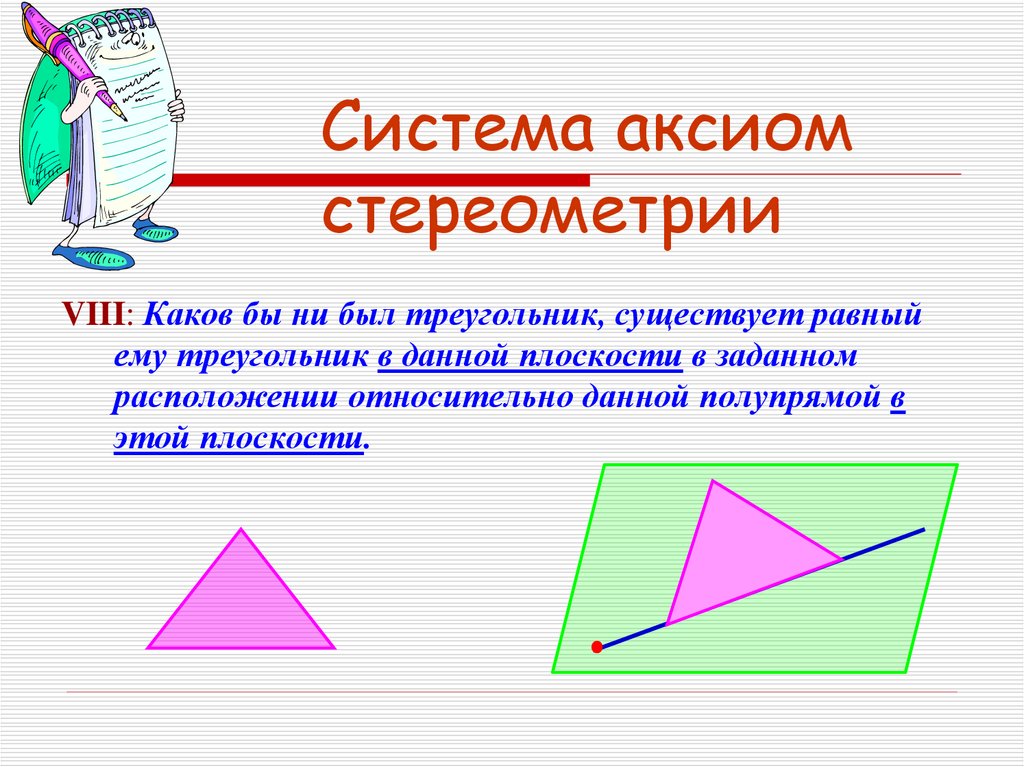
VIII: Каков бы ни был треугольник, существует равныйему треугольник в данной плоскости в заданном
расположении относительно данной полупрямой в
этой плоскости.
17. Система аксиом стереометрии
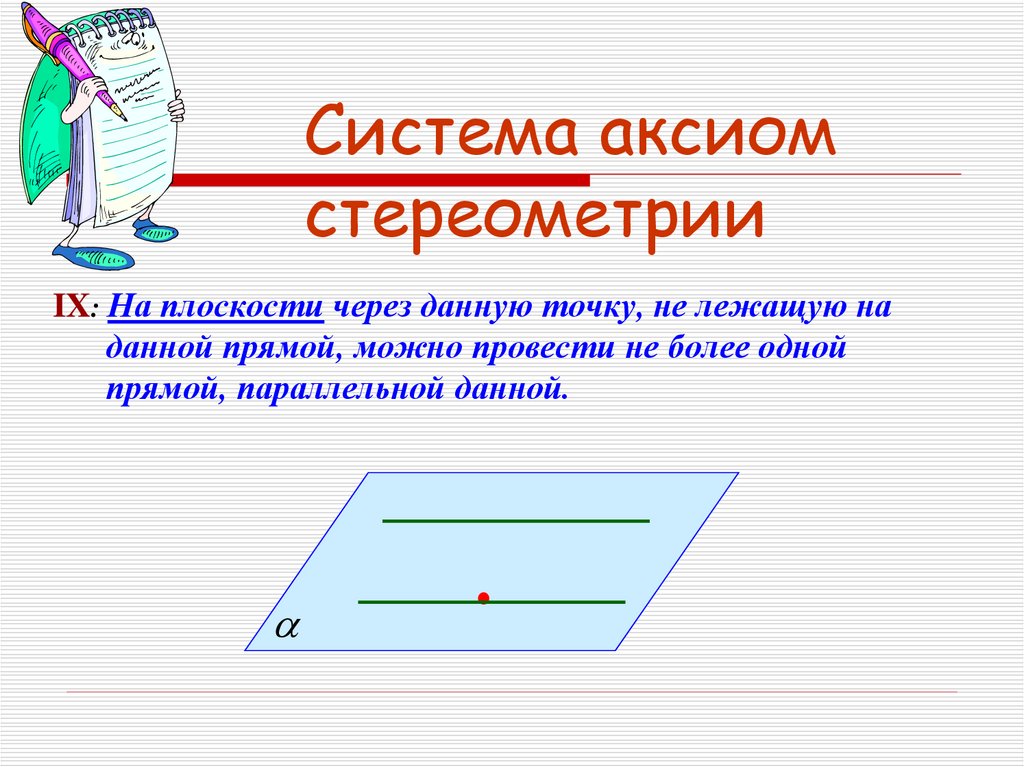
IX: На плоскости через данную точку, не лежащую наданной прямой, можно провести не более одной
прямой, параллельной данной.
18. Система аксиом стереометрии
С1: Какова бы ни была плоскость, существуют точки,принадлежащие этой плоскости, и точки, не
принадлежащие ей.
С2: Если две различные плоскости имеют общую точку,
то они пересекаются по прямой, проходящей через
эту точку.
С3: Если две различные прямые имеют общую точку, то
через них можно провести плоскость, и притом
только одну.
19. Решение задач
По рисунку ответьте на вопросы:C
A
B
D
F
1) Какие точки принадлежат плоскости α?
2) Какие точки не принадлежат плоскости α?
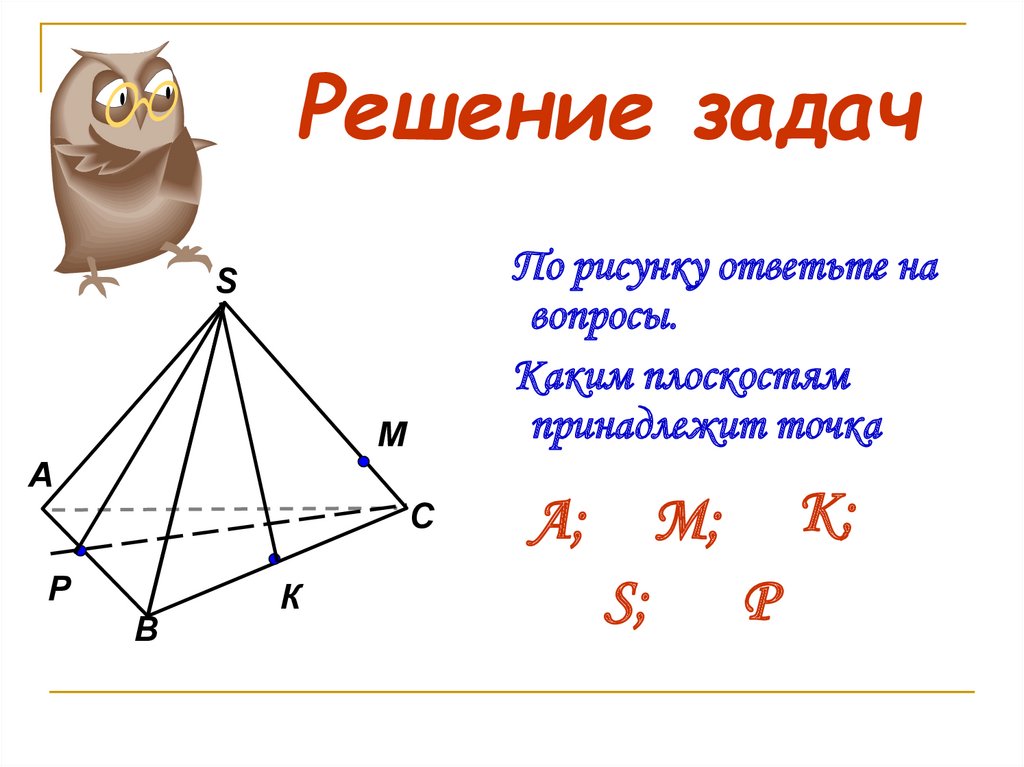
20. Решение задач
По рисунку ответьте навопросы.
Каким плоскостям
принадлежит точка
S
М
А
С
Р
В
К
А;
К;
М;
S;
P
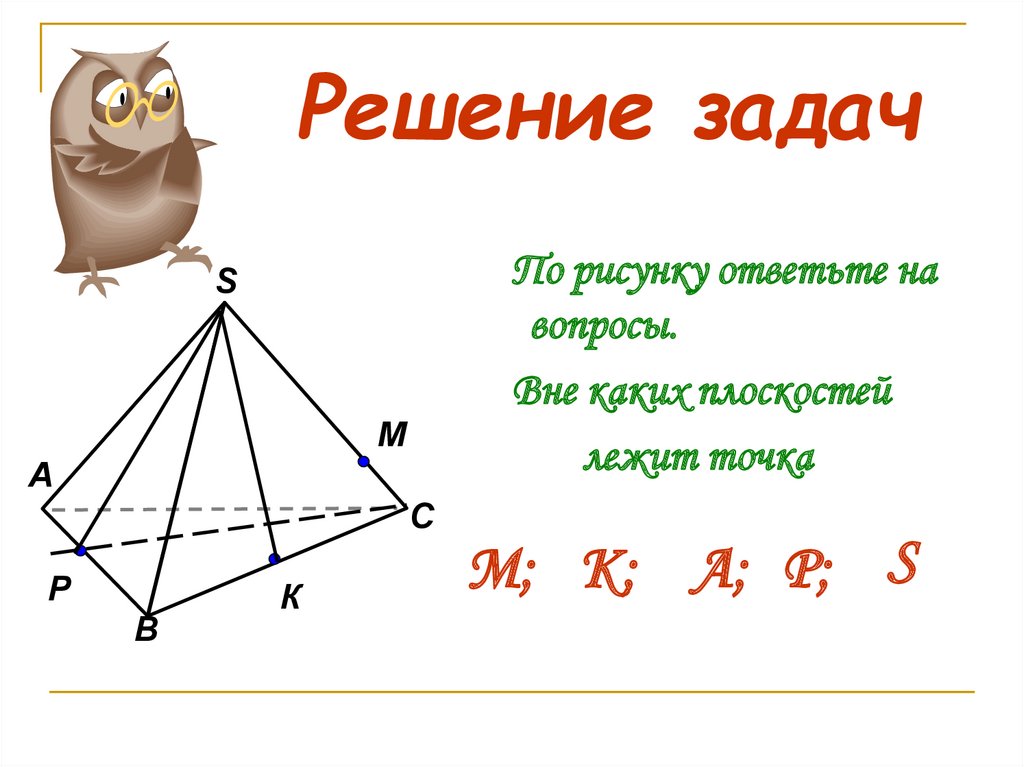
21. Решение задач
По рисунку ответьте навопросы.
Вне каких плоскостей
лежит точка
S
М
А
С
Р
В
К
М; К; А; P; S
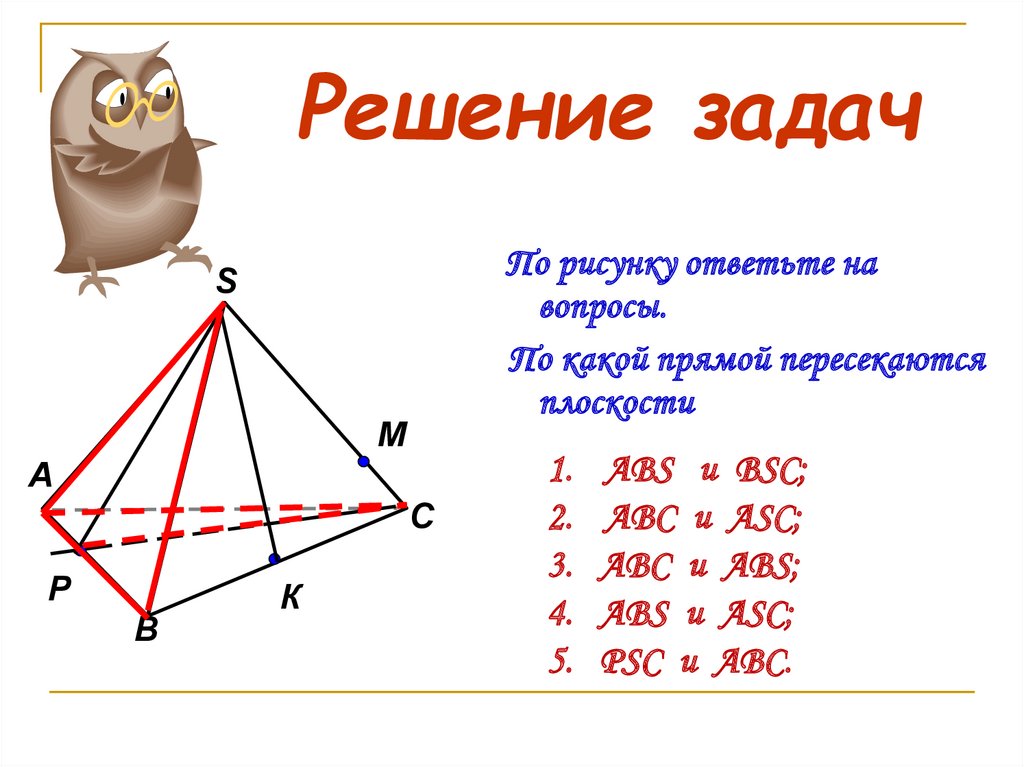
22. Решение задач
По рисунку ответьте навопросы.
По какой прямой пересекаются
плоскости
S
М
А
С
Р
В
К
1.
2.
3.
4.
5.
ABS и BSC;
ABC и ASC;
ABC и ABS;
ABS и ASC;
PSC и ABC.
23. Решение задач
Могут ли две различные плоскостииметь только одну общую точку?
Каково взаимное расположение двух прямых
пространстве, если они имеют две общие точки?
Могут ли две различные прямые в пространстве
иметь более одной общей точки?
24. Решение задач
Столяр проверяет, лежат ли ножкистула в одной плоскости, при помощи
двух нитей. Объясните, как он это
делает.
25. Решение задач
Докажите, что все вершинычетырёхугольника принадлежат одной
плоскости, если его диагонали
пересекаются.















 mathematics
mathematics








