Similar presentations:
Стереометрия .Аксиомы и их следствия
1.
Аксиомыстереометрии.
Некоторые
следствия
из аксиом.
2. Геометрия
ПланиметрияСтереометрия
stereos
телесный, твердый,
объемный,
пространственный
3. Стереометрия.
-Раздел геометрии, в которомизучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Плоскость.
Прямая.
4.
A, B, C, …a, b, c, …
или
AВ, BС, CD, …
, , ,
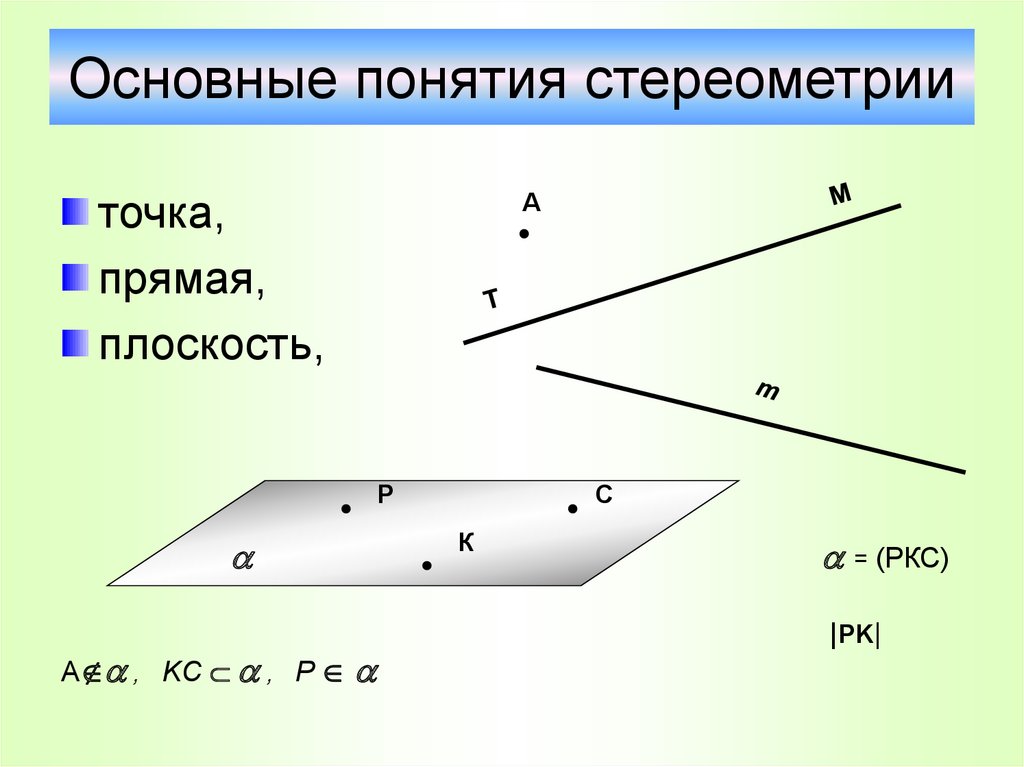
5. Основные понятия стереометрии
точка,прямая,
плоскость,
А
Р
К
A , KC , P
С
= (РКС)
|PK|
6. Геометрические тела:
Куб.Тетраэдр.
Параллелепипед.
7.
Рассмотрим геометрические тела, поверхностькоторых составлена из многоугольников.
Такие поверхности называются
МНОГОГРАННИКАМИ
•Стороны и вершины этих многоугольников
называются ребрами и вершинами.
•Отрезки, соединяющие вершины многогранника,
не принадлежащие одной грани, называются
дигоналями.
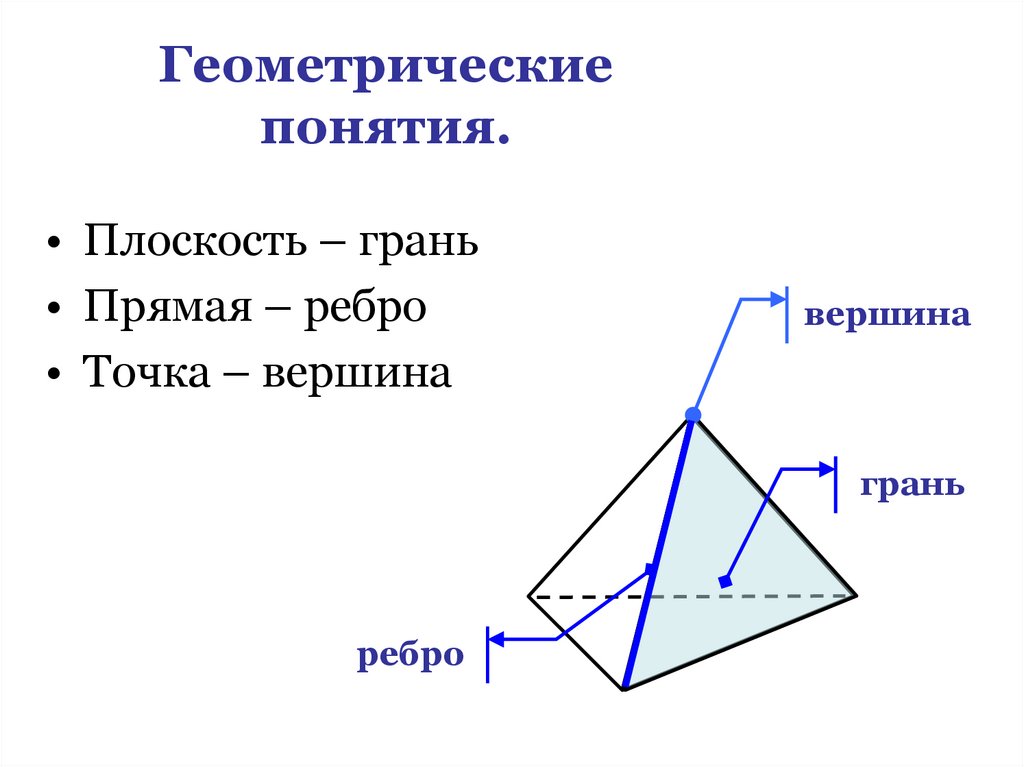
8. Геометрические понятия.
• Плоскость – грань• Прямая – ребро
• Точка – вершина
вершина
грань
ребро
9. Аксиома
(от греч. axíõma – принятие положения)исходное положение
научной теории,
принимаемое без
доказательства
10. Определите: верно, ли суждение?
В стереометрии мы будем рассматривать ситуации, задающие различныерасположения в пространстве основных фигур относительно друг друга
Определите: верно, ли суждение?
1.
2.
3.
4.
5.
6.
7.
8.
ДА
Любые три точки лежат в одной плоскости.
НЕТ
Любые четыре точки лежат в одной плоскости.
Любые четыре точки не лежат в одной плоскости.
НЕТ
Через любые три точки проходит плоскость и при том
НЕТ
только одна.
Если прямая пересекает 2 стороны треугольника, то
ДА
она лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то НЕТ
она лежит в плоскости треугольника.
НЕТ
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны. ДА
11. Аксиомы стереометрии
Через любые три точки, не лежащие на одной прямойпроходит плоскость, и притом только одна
А-1
Р
С
К
= (РКС)
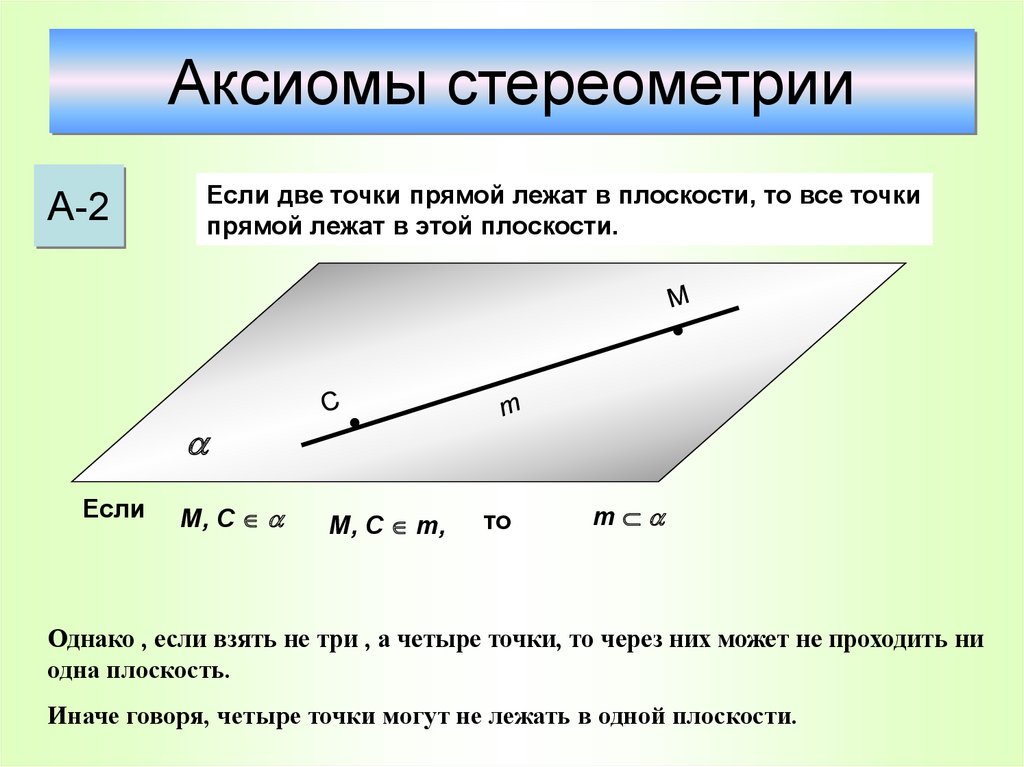
12. Аксиомы стереометрии
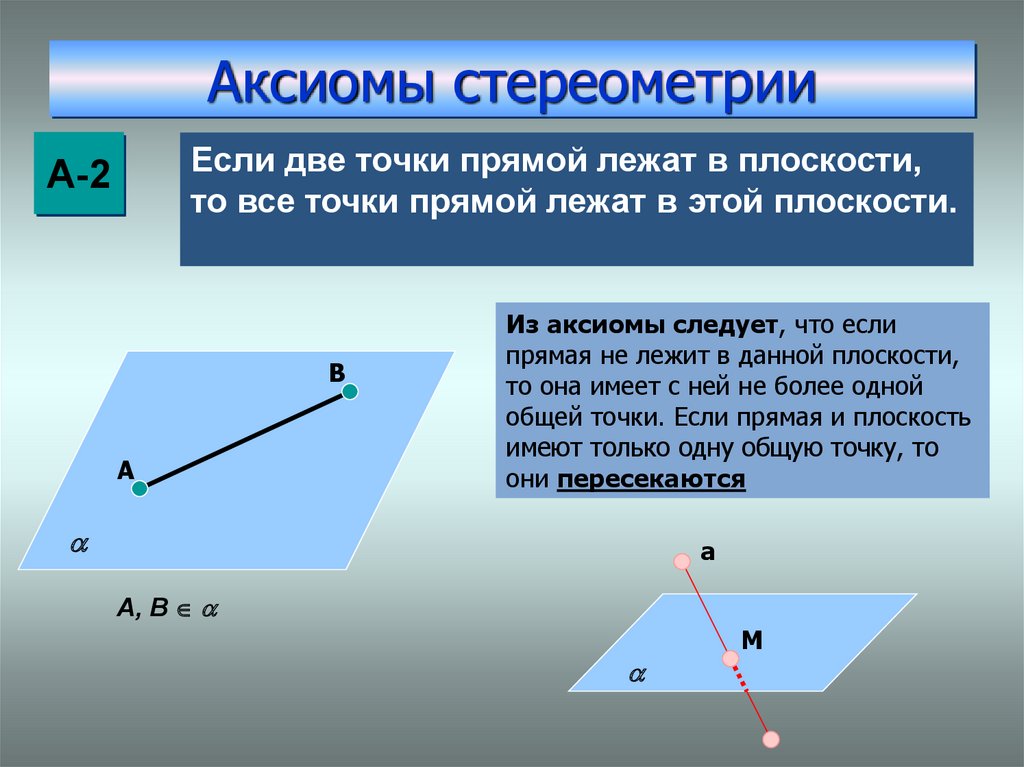
А-2Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Если
М, C
М, C m,
то
m
Однако , если взять не три , а четыре точки, то через них может не проходить ни
одна плоскость.
Иначе говоря, четыре точки могут не лежать в одной плоскости.
13. Аксиомы стереометрии
Если две точки прямой лежат в плоскости,то все точки прямой лежат в этой плоскости.
А-2
В
А
Из аксиомы следует, что если
прямая не лежит в данной плоскости,
то она имеет с ней не более одной
общей точки. Если прямая и плоскость
имеют только одну общую точку, то
они пересекаются
a
А, В
М
14. Аксиомы стереометрии
Если две плоскости имеют общую точку, то они имеютобщую прямую, на которой лежат все общие точки
этих плоскостей.
А-3
М , М , М m
М
m , m
=m
15.
Аксиомы стереометрии описывают:А1.
Способ
задания
плоскости.
А2.
Взаимное
расположение
прямой и
плоскости
А3.
Взаимное
расположение
плоскостей
А
В
А
С
В
16.
Взаимное расположение прямой и плоскости.Прямая
лежит в
плоскости.
Прямая
пересекает
плоскость.
а
Множество
общих
точек.
а
М
а
Прямая не
пересекает
плоскость.
а
а М
Единственная
общая точка.
а
Нет общих
точек.
А2
17.
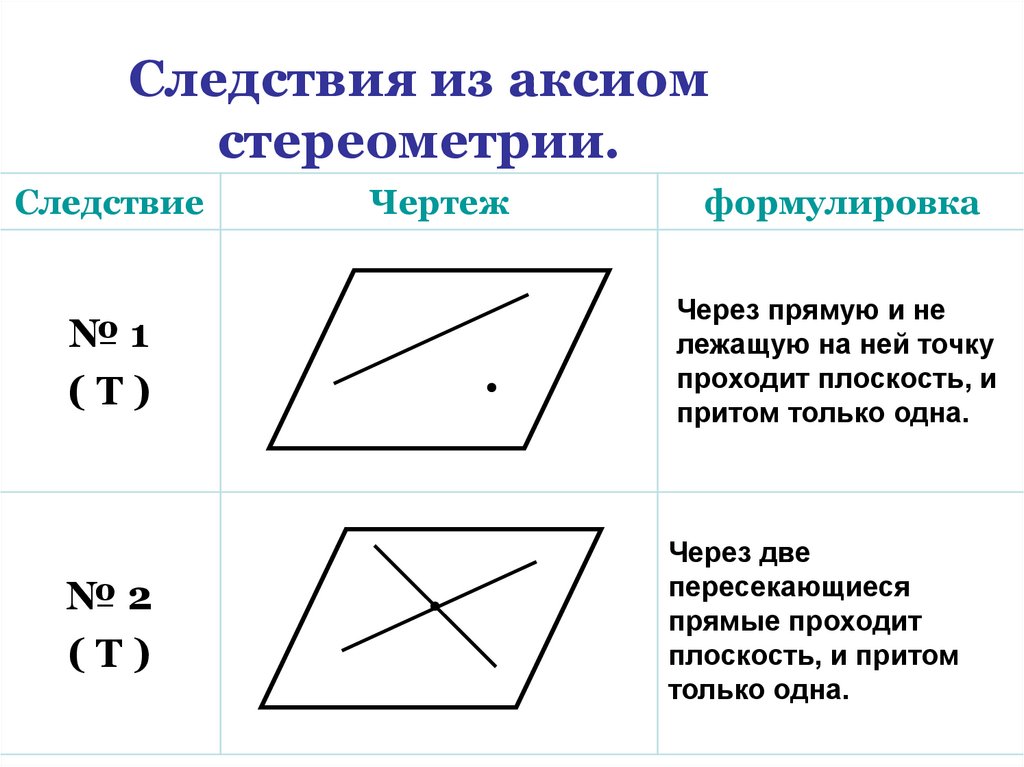
Следствия из аксиомстереометрии.
Следствие
Чертеж
формулировка
№1
(Т)
Через прямую и не
лежащую на ней точку
проходит плоскость, и
притом только одна.
№2
(Т)
Через две
пересекающиеся
прямые проходит
плоскость, и притом
только одна.
18.
СЛЕДСТВИЯ ИЗ АКСИОМЧерез любую прямую и не принадлежащую ей точку
можно провести плоскость, и притом только одну.
Т-1
Дано: М m
В
А
м
Доказательство
Пусть точки A, B m.
Так как М m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM),
Обозначим её . Прямая m имеет с ней две общие точки — точки A и B, следовательно,
по аксиоме А-2 эта прямая лежит в плоскости ..
Таким образом, плоскость проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует.
Предположим, что есть другая плоскость — , проходящая через прямую m и точку M.
Тогда плоскости и проходят через точки А, В и M, не принадлежащие одной прямой, а
значит, совпадают. Следовательно, плоскость единственна.
Теорема доказана
19. Следствия из аксиом стереометрии.
СЛЕДСТВИЯ ИЗ АКСИОМЧерез любые две пересекающиеся прямые можно
провести плоскость, и притом только одну.
Т-2
n
м
N
Дано: m n = M
Доказательство
Отметим на прямой m произвольную точку N,
отличную от М.
Рассмотрим плоскость =(n, N). Так как M и N , то по А-2 m . Значит
обе прямые m, n лежат в плоскости и следовательно , является искомой
Докажем единственность плоскости . Допустим, что есть другая, отличная от
плоскости и проходящая через прямые m и n, плоскость .
Так как плоскость проходит через прямую n и не принадлежащую ей точку N, то по
T-1 она совпадает с плоскостью . Единственность плоскости доказана.
Теорема доказана
20. СЛЕДСТВИЯ ИЗ АКСИОМ
ВЫВОДКак в пространстве можно однозначно задать плоскость?
По трем точкам, не лежащим на одной прямой
По прямой и точке, не лежащей на этой прямой
По двум пересекающимся прямым
По двум параллельным прямым
21. СЛЕДСТВИЯ ИЗ АКСИОМ
ОТВЕТЬТЕ НА ВОПРОСЫ1.
2.
Сколько существует способов задания плоскости?
Сколько плоскостей можно провести через выделенные элементы?
а)
г)
б)
д)
в)
е)
22. ВЫВОД
Дз• Выучи наизусть формулировки аксиом и
следствий
• Ответь на вопросы№3,4,5,6,8,10,13
• Подготовь конспект параграфа
(формулировки и определения)
• Закончи работу с презентацией
23. ОТВЕТЬТЕ НА ВОПРОСЫ
Прочти чертежС
A
A
C
24. Дз
Прочти чертежb
B
c
a
b B
a
c
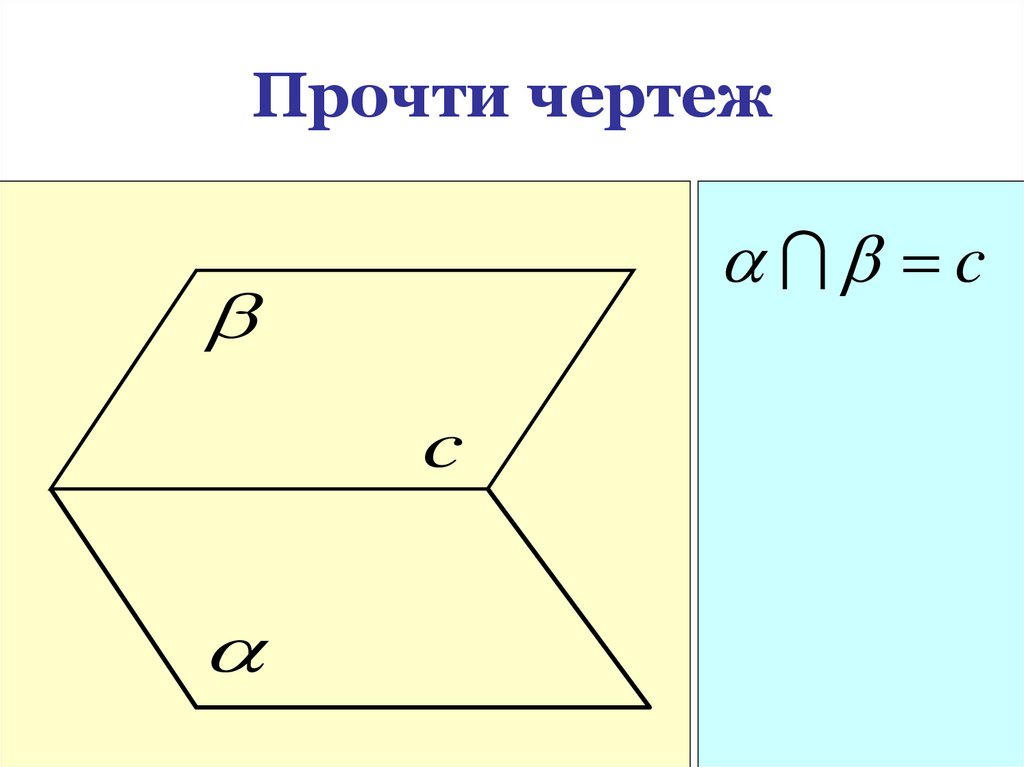
25. Прочти чертеж
cc
26. Прочти чертеж
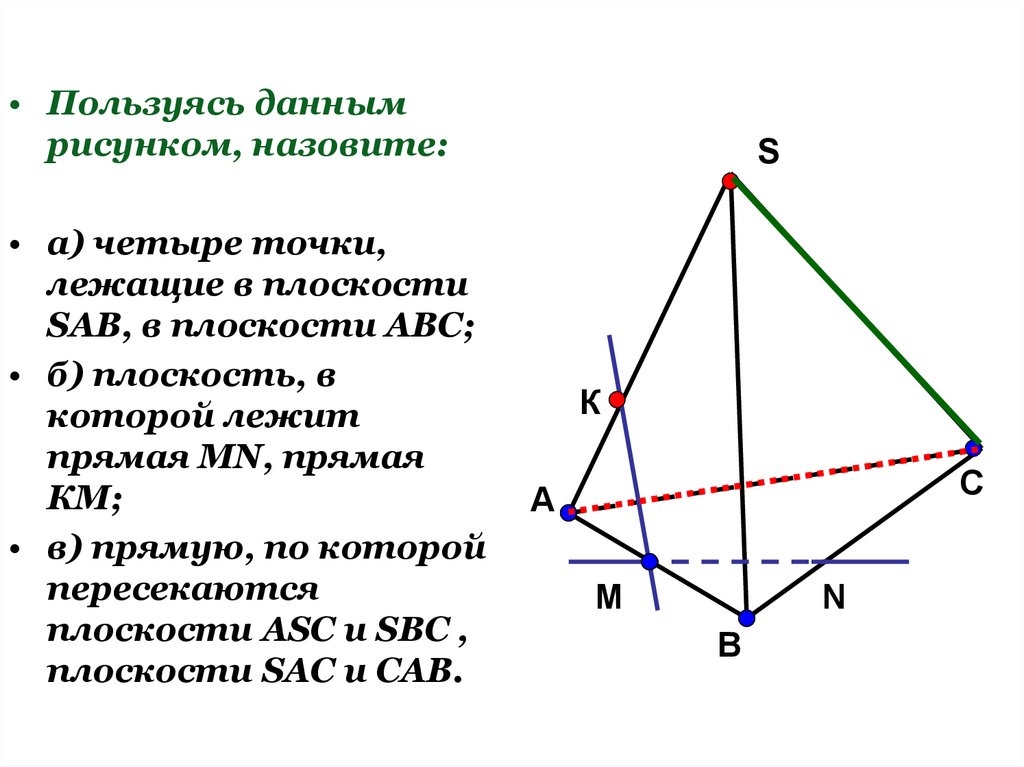
• Пользуясь даннымрисунком, назовите:
• а) четыре точки,
лежащие в плоскости
SAB, в плоскости АВС;
• б) плоскость, в
которой лежит
прямая MN, прямая
КМ;
• в) прямую, по которой
пересекаются
плоскости ASC и SBC ,
плоскости SAC и CAB.
S
К
C
А
М
N
В
27. Прочти чертеж
• Пользуясь даннымрисунком, назовите:
• а) две плоскости,
содержащие прямую
DE , прямую EF
• б) прямую, по которой
пересекаются
плоскости
DEF и SBC; плоскости
FDE и SAC ;
• в) две плоскости,
которые пересекает
прямая SB; прямая AC .
S
E
D
С
А
F
В
28.
• Пользуясь даннымрисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
B1
A1
C1
D1
B
A
C
D
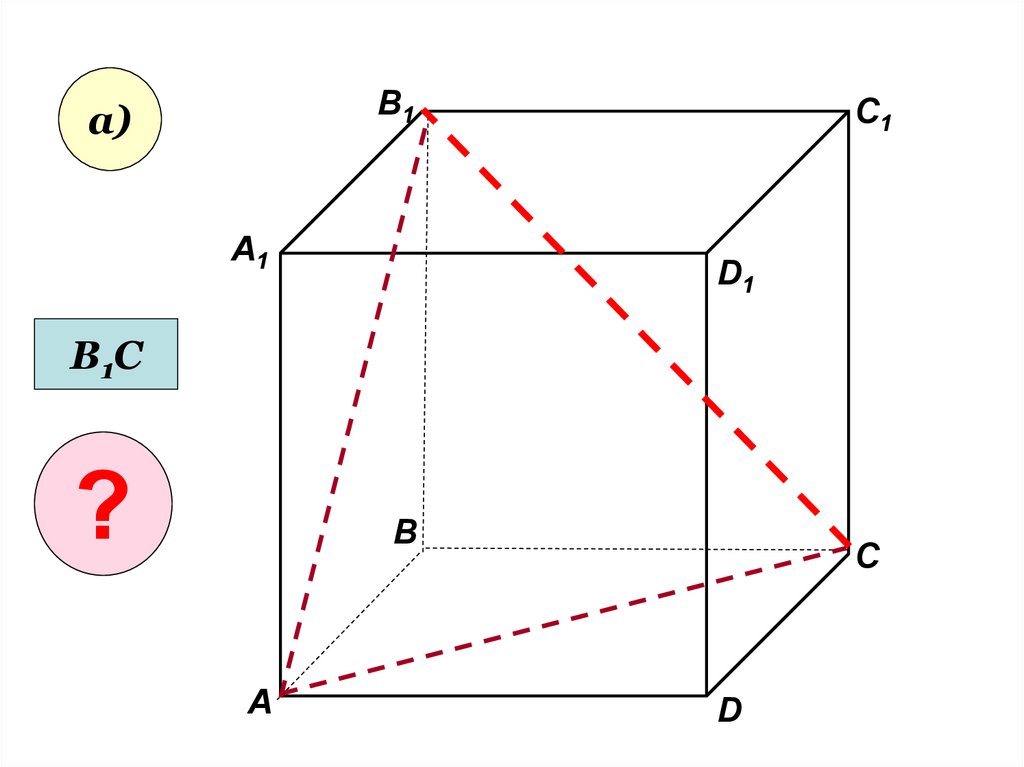
29.
В1а)
А1
C1
D1
В1С
?
В
А
С
D
30.
В1а)
А1
C1
D1
В1С
?
В
А
С
D
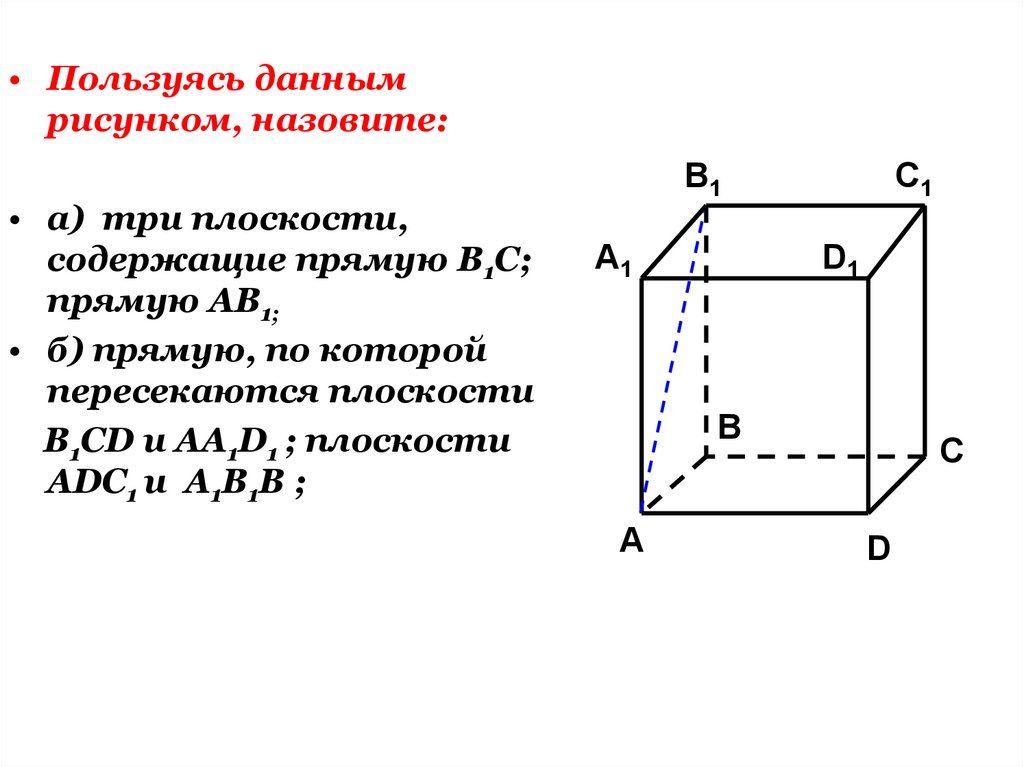
31.
• Пользуясь даннымрисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
B1
A1
C1
D1
B
A
C
D
32.
В1б)
А1
C1
D1
В
А
С
D
33.
• Пользуясь даннымрисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
C
1
A1
D1
B
A
C
D
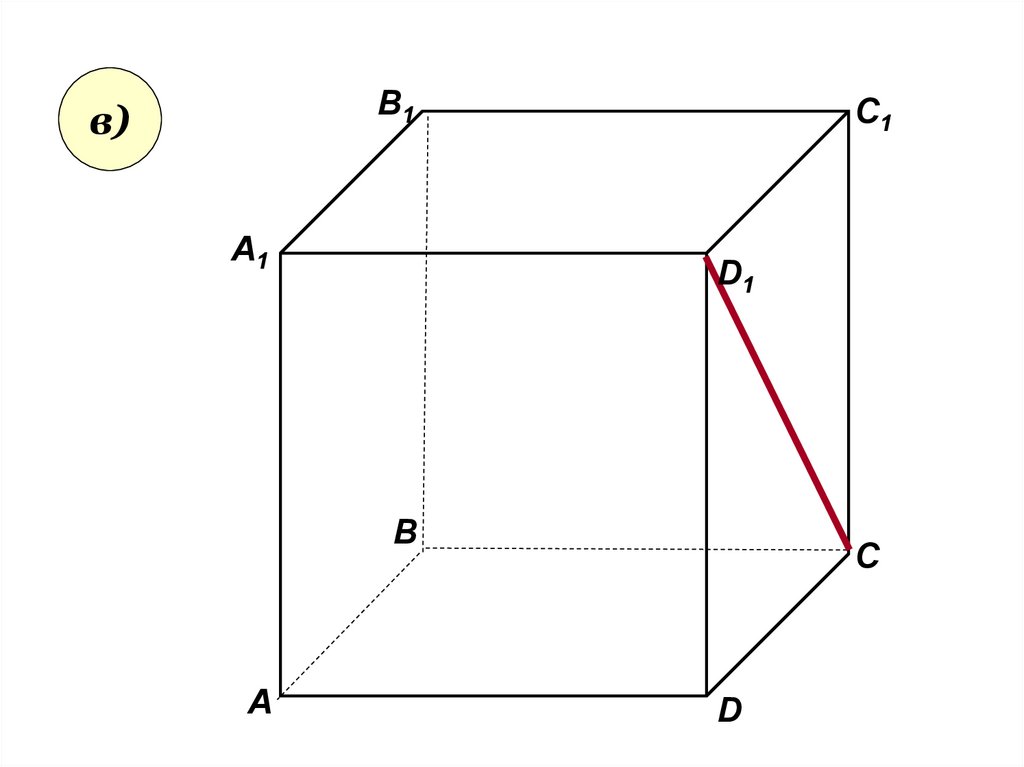
34.
В1в)
А1
C1
D1
В
А
С
D
35.
• Пользуясь даннымрисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
C
1
A1
D1
B
A
C
D
























 mathematics
mathematics








