Аксиомы стереометрии. Взаимное расположение двух прямых. Взаимное расположение прямой и плоскости

1.

Аксиомы
стереометрии
Взаимное
расположение двух
прямых
Взаимное
расположение прямой
и плоскости

2. Геометрия

Планиметрия
Стереометрия
stereos
- объемный, пространственный
metreo - измеряю

3. Стереометрия

-раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве
А
Точка.
а
Плоскость.
Прямая.

4.

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
, , ,

5. Геометрические тела

Куб.
Тетраэдр.
Параллелепипед.

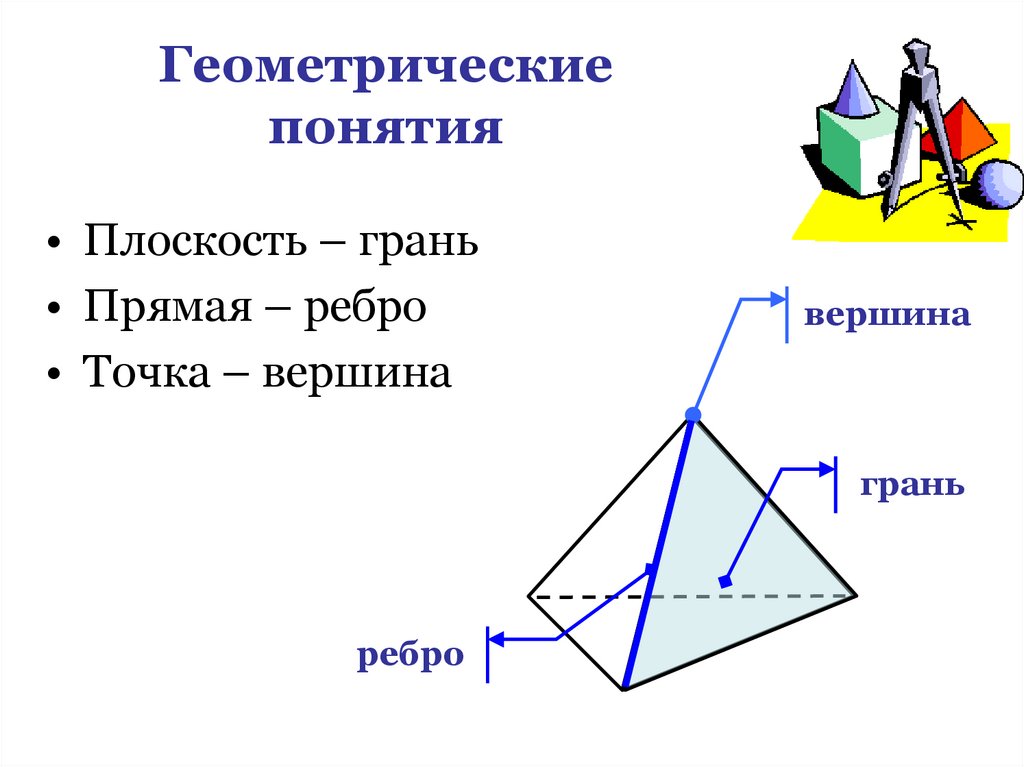
6. Геометрические понятия

• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро

7. Аксиома

(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

8.

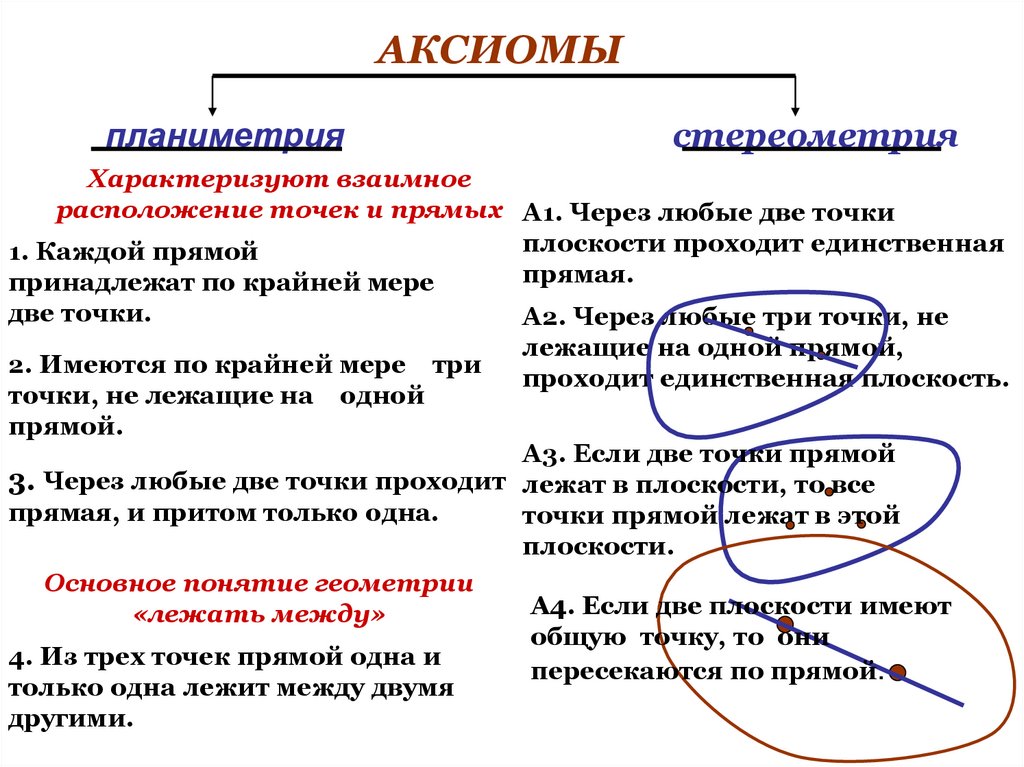
АКСИОМЫ
планиметрия
стереометрия
Характеризуют взаимное
расположение точек и прямых А1. Через любые две точки
плоскости проходит единственная
1. Каждой прямой
прямая.
принадлежат по крайней мере
две точки.
2. Имеются по крайней мере три
точки, не лежащие на одной
прямой.
А2. Через любые три точки, не
лежащие на одной прямой,
проходит единственная плоскость.
А3. Если две точки прямой
3. Через любые две точки проходит лежат в плоскости, то все
прямая, и притом только одна.
точки прямой лежат в этой
плоскости.
Основное понятие геометрии
А4. Если две плоскости имеют
«лежать между»
общую точку, то они
4. Из трех точек прямой одна и
пересекаются по прямой.
только одна лежит между двумя
другими.

9.

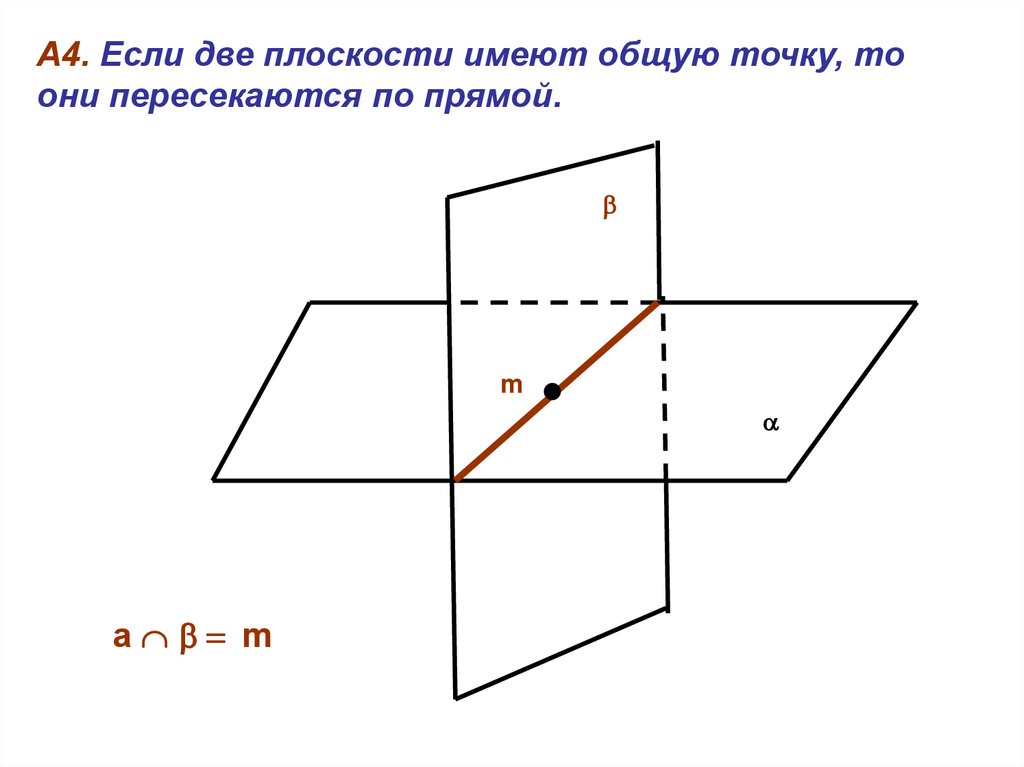
А4. Если две плоскости имеют общую точку, то
они пересекаются по прямой.
m
а m

10.

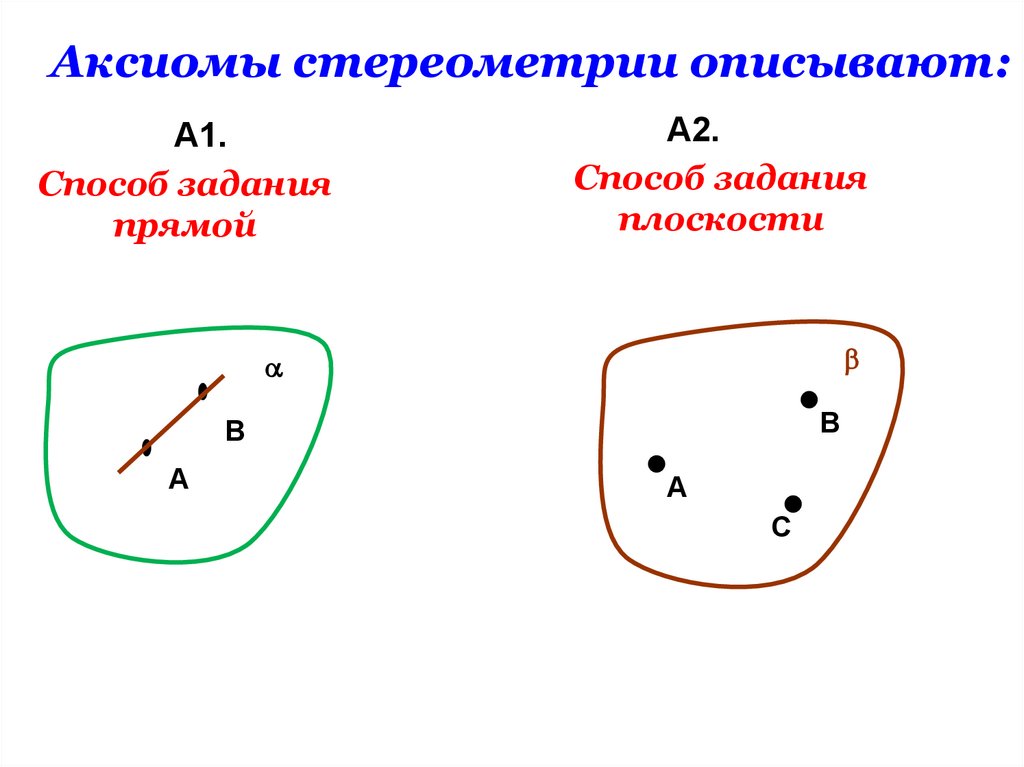
Аксиомы стереометрии описывают:
А1.
Способ задания
прямой
А2.
Способ задания
плоскости
В
В
А
А
С

11.

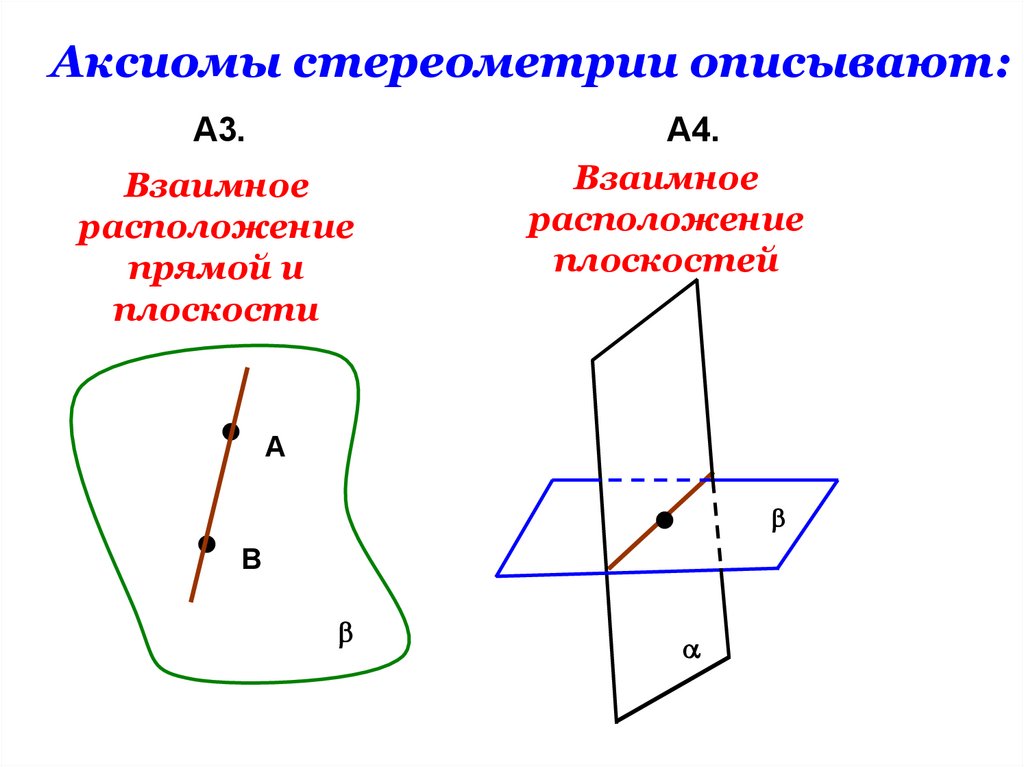
Аксиомы стереометрии описывают:
А3.
Взаимное
расположение
прямой и
плоскости
А4.
Взаимное
расположение
плоскостей
А
В

12.

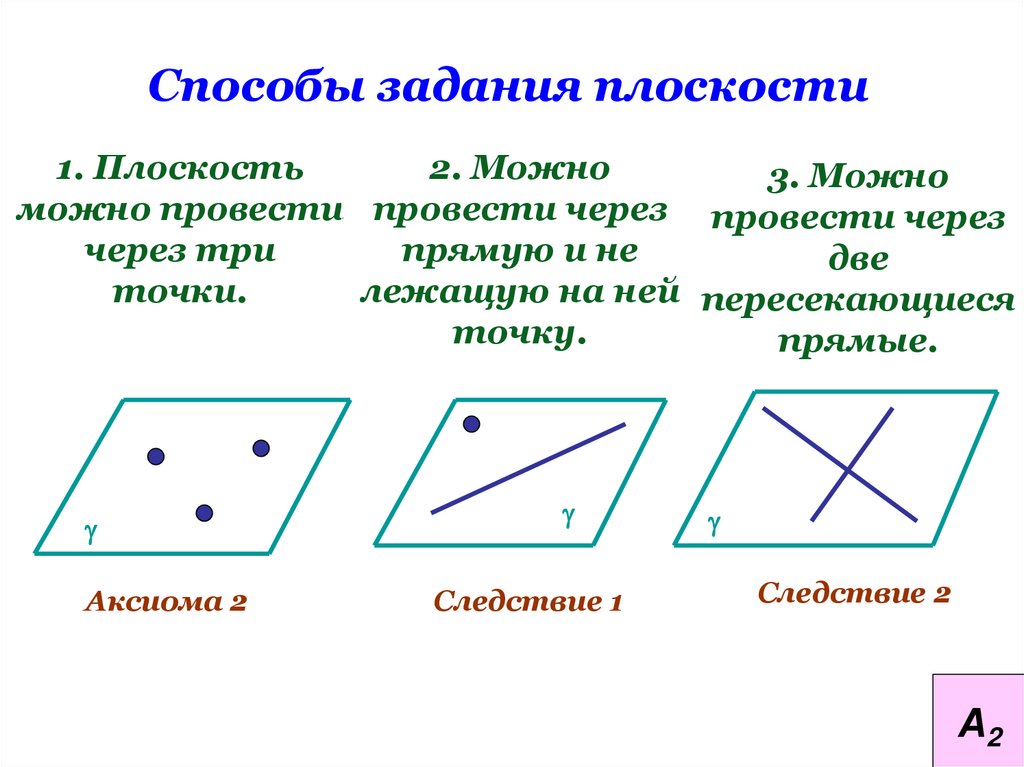
Способы задания плоскости
1. Плоскость
2. Можно
3. Можно
можно провести провести через провести через
через три
прямую и не
две
точки.
лежащую на ней пересекающиеся
точку.
прямые.
Аксиома 2
Следствие 1
Следствие 2
А2

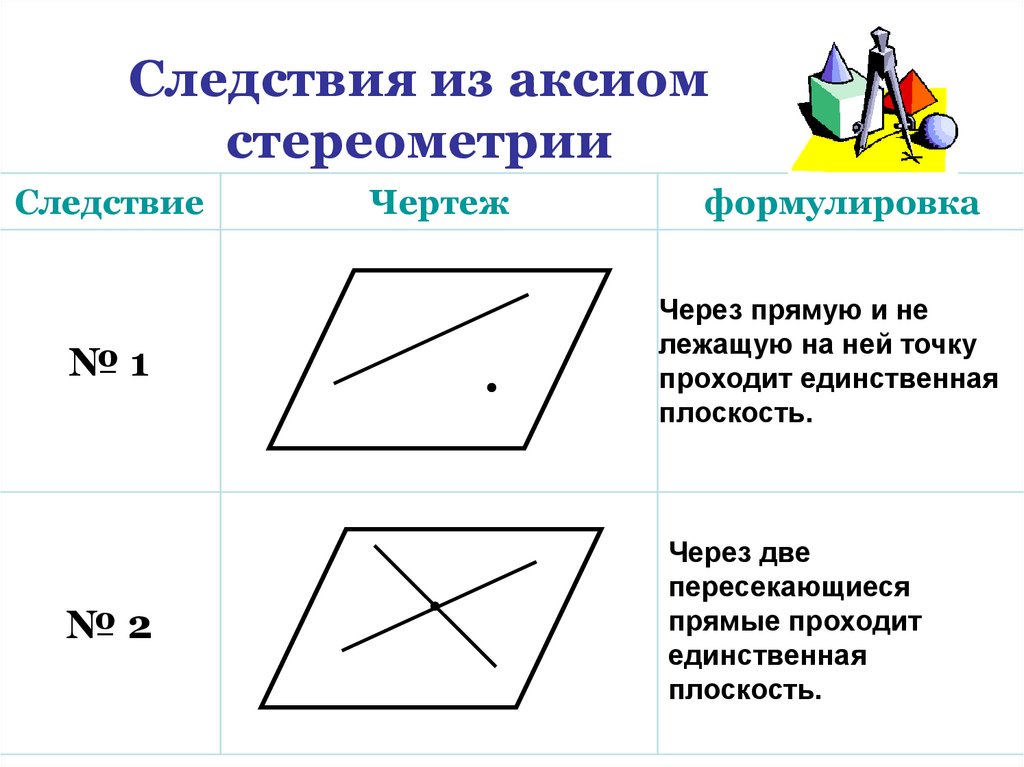
13. Следствия из аксиом стереометрии

Следствие
Чертеж
формулировка
№1
Через прямую и не
лежащую на ней точку
проходит единственная
плоскость.
№2
Через две
пересекающиеся
прямые проходит
единственная
плоскость.

14.

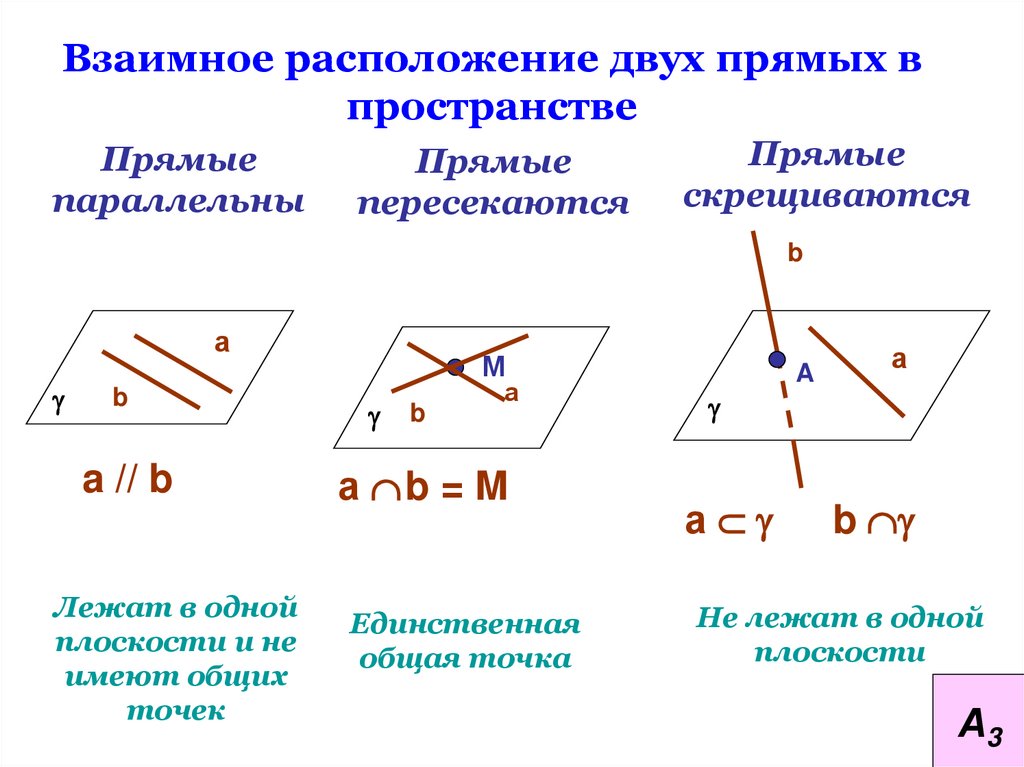
Взаимное расположение двух прямых в
пространстве
Прямые
параллельны
Прямые
пересекаются
Прямые
скрещиваются
b
а
b
a // b
Лежат в одной
плоскости и не
имеют общих
точек
М
b
а
а b = M
Единственная
общая точка
A
а
а
b
Не лежат в одной
плоскости
А3

15.

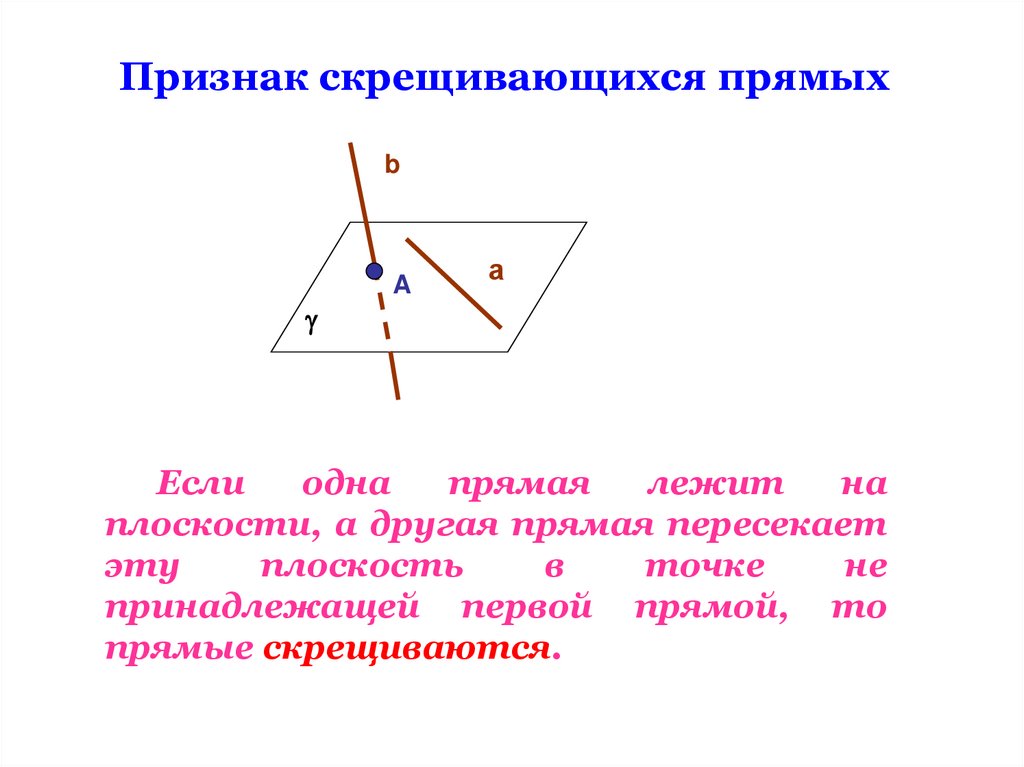
Признак скрещивающихся прямых
b
A
а
Если
одна
прямая
лежит
на
плоскости, а другая прямая пересекает
эту
плоскость
в
точке
не
принадлежащей первой прямой, то
прямые скрещиваются.

16.

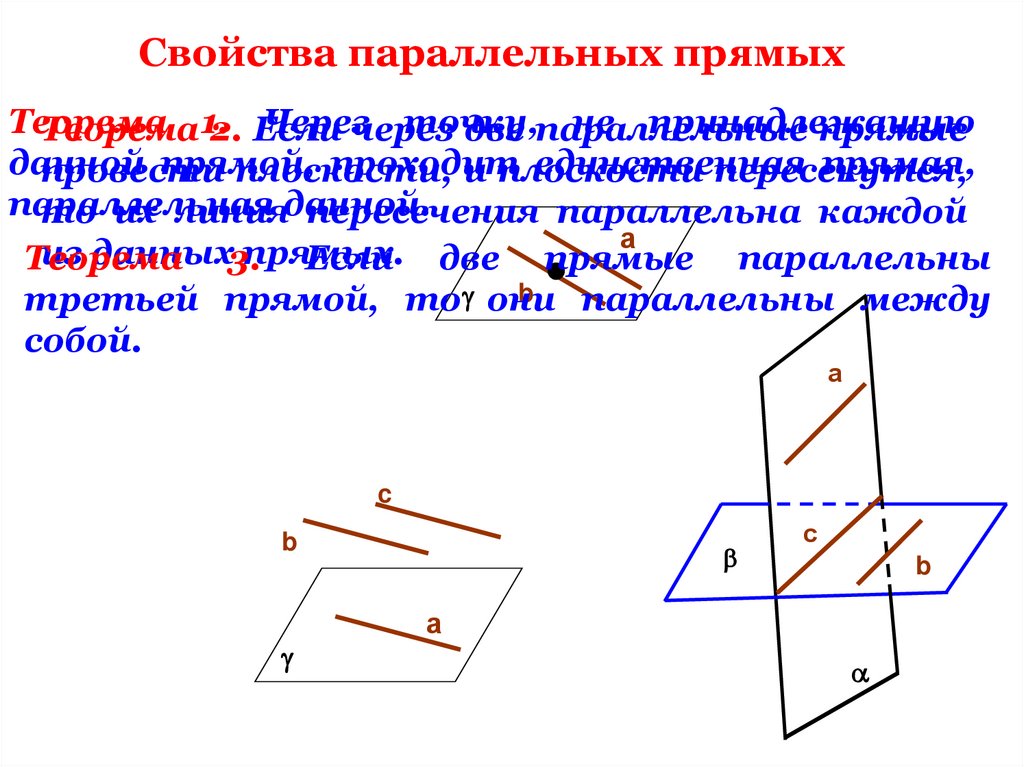
Свойства параллельных прямых
Теорема
Через
точку,
не принадлежащую
Теорема 1.
2. Если
через
две параллельные
прямые
данной
прямой,
проходит
единственная
прямая,
провести
плоскости,
и плоскости
пересекутся,
параллельная
то их линияданной.
пересечения параллельна каждой
а
из
данных
прямых.
Теорема 3. Если две прямые параллельны
b
третьей прямой, то они
параллельны между
собой.
а
c
b
с
b
а

17.

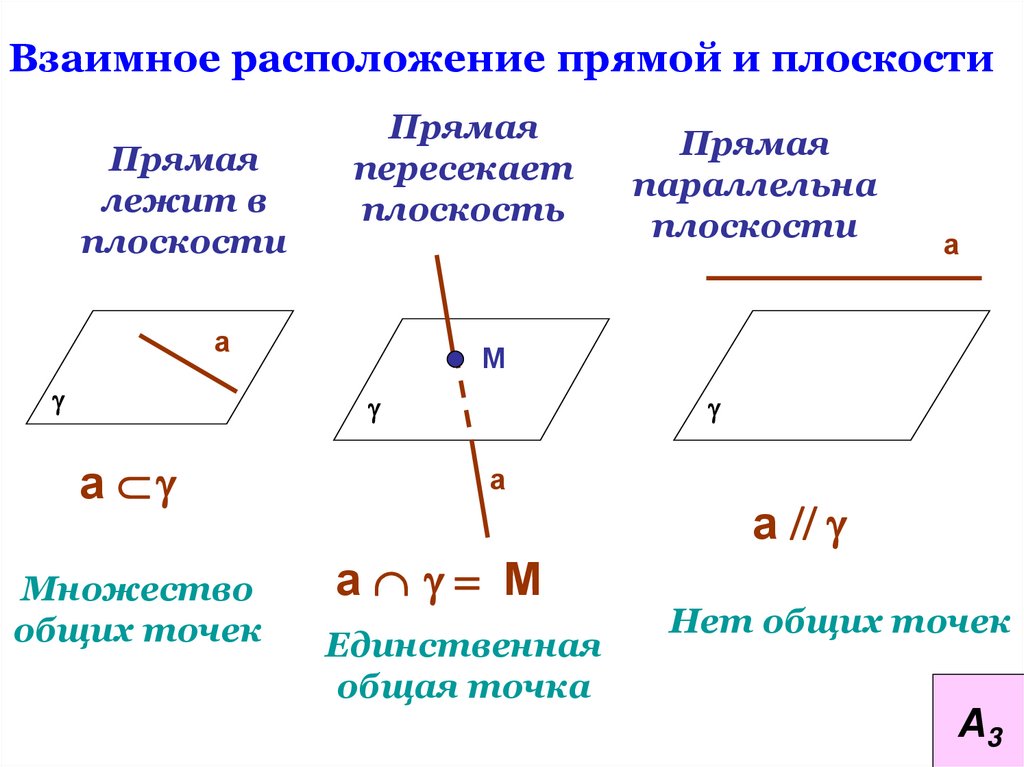
Взаимное расположение прямой и плоскости
Прямая
лежит в
плоскости
Прямая
пересекает
плоскость
а
Множество
общих точек
а
М
а
Прямая
параллельна
плоскости
а
а М
Единственная
общая точка
а //
Нет общих точек
А3

18. Прочти чертеж

С
A
A
C

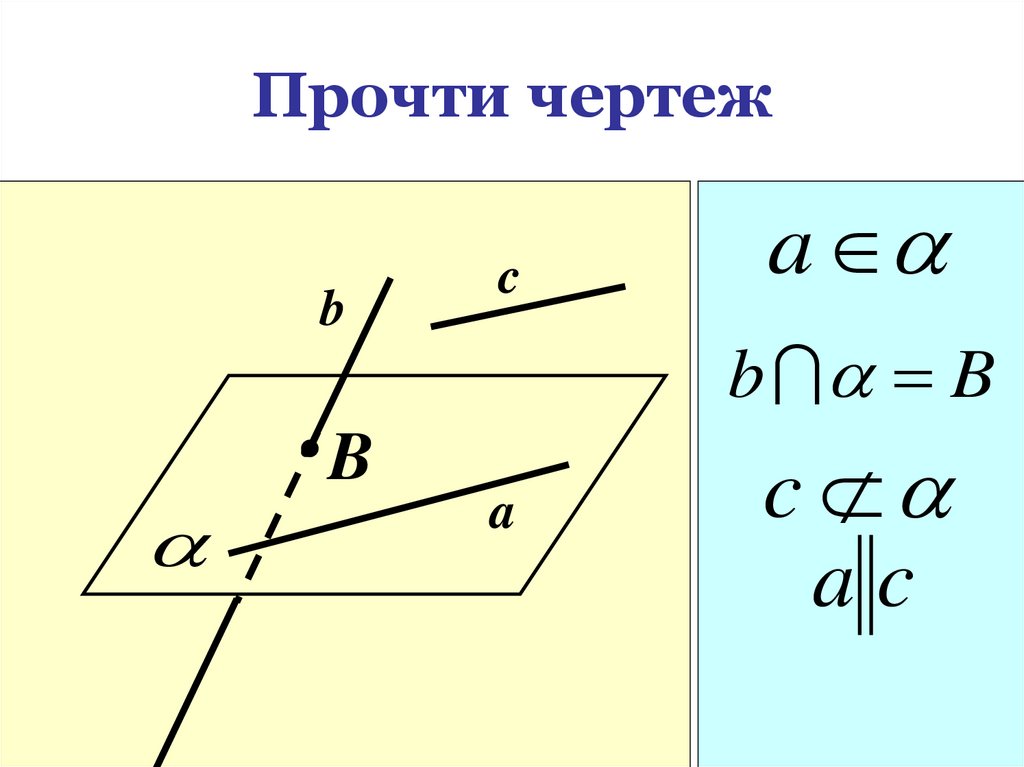
19. Прочти чертеж

b
B
c
a
b B
a
c
ac

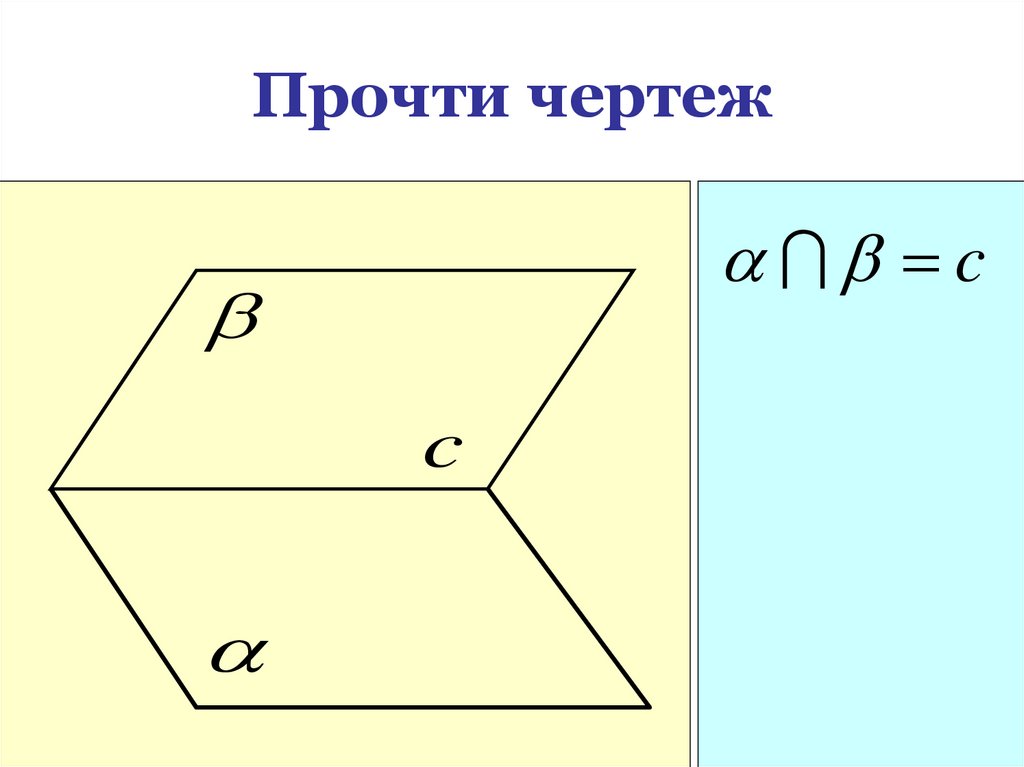
20. Прочти чертеж

c
c

21.

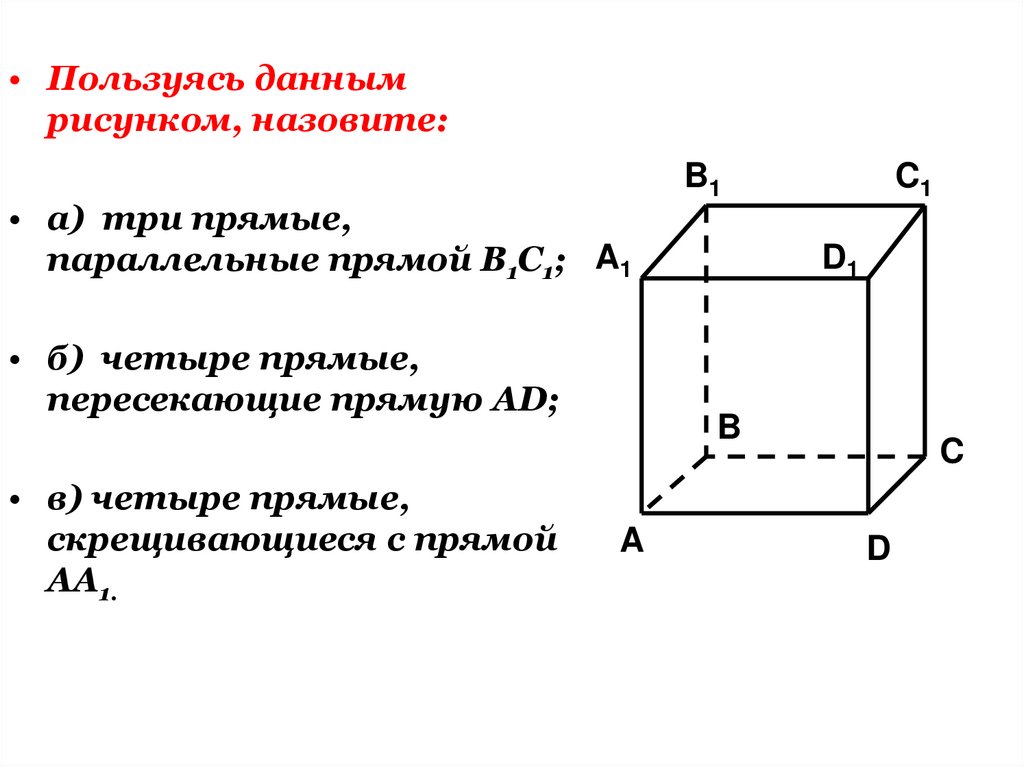
• Пользуясь данным
рисунком, назовите:
• а) три прямые,
параллельные прямой В1С1; A1
• б) четыре прямые,
пересекающие прямую AD;
• в) четыре прямые,
скрещивающиеся с прямой
АА1.
B1
C1
D1
B
A
C
D

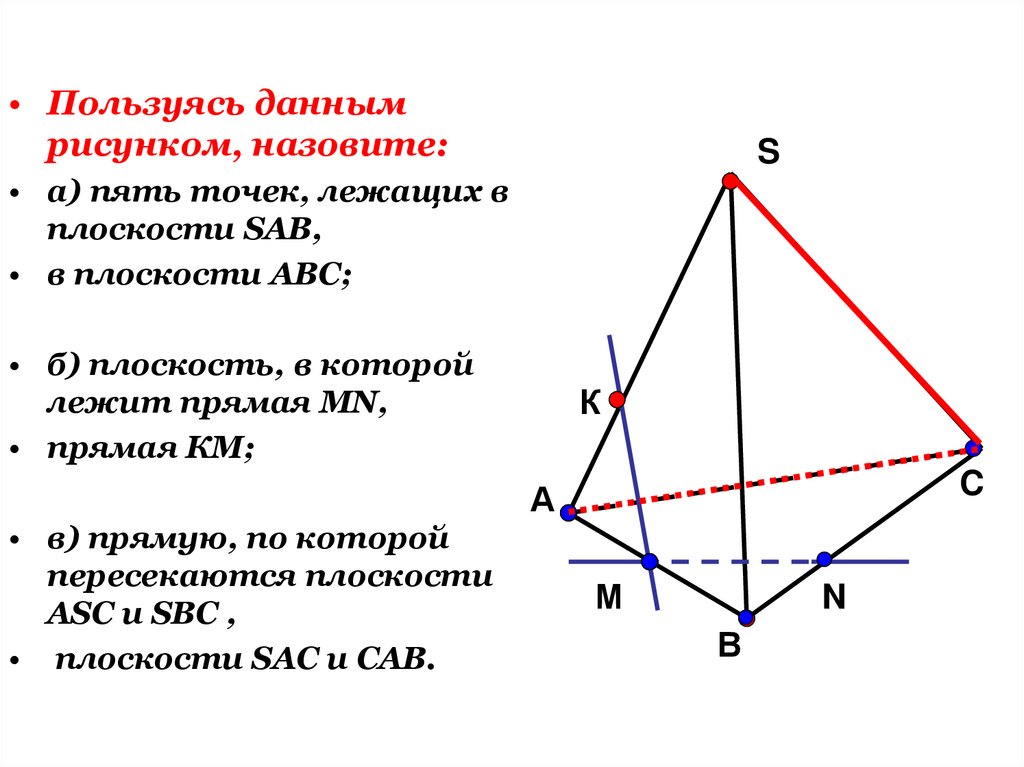
22.

• Пользуясь данным
рисунком, назовите:
S
• а) пять точек, лежащих в
плоскости SAB,
• в плоскости АВС;
• б) плоскость, в которой
лежит прямая MN,
• прямая КМ;
К
C
А
• в) прямую, по которой
пересекаются плоскости
ASC и SBC ,
• плоскости SAC и CAB.
М
N
В

23.

• Пользуясь данным
рисунком, назовите:
• а) две плоскости,
содержащие прямую DE ,
• прямую EF;
D
• б) прямую, по которой
пересекаются плоскости
А
DEF и SBC;
• плоскости FDE и SAC ;
• в) две плоскости, которые
пересекает прямая SB;
прямая AC .
S
E
С
F
В

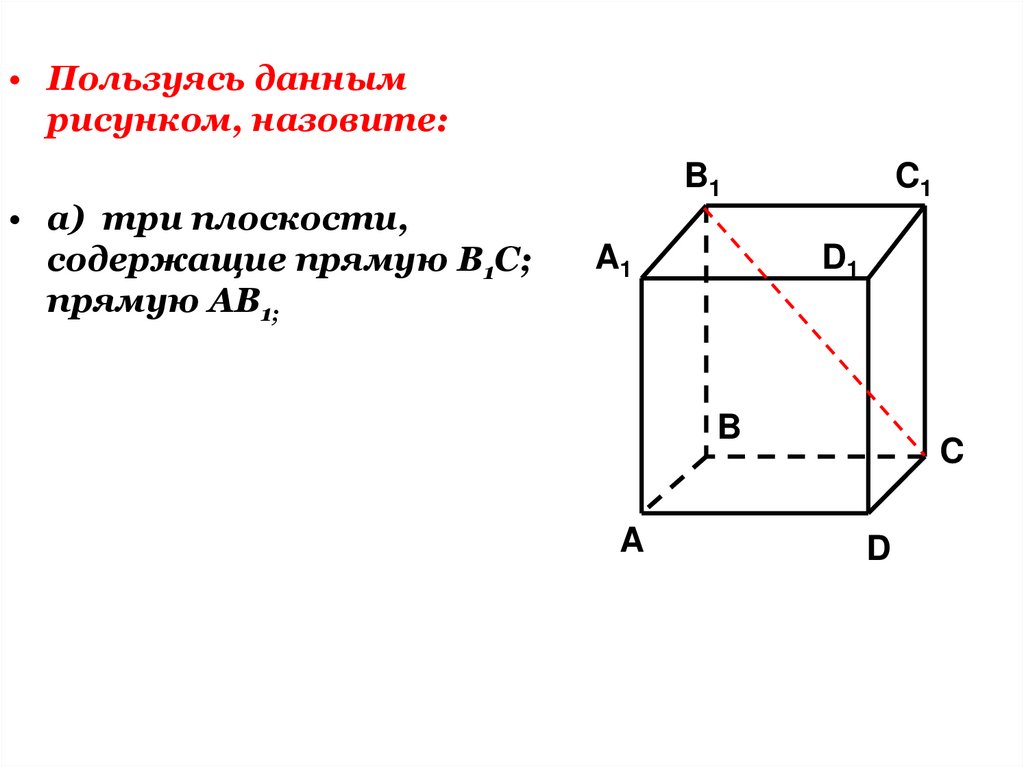
24.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
B1
A1
C1
D1
B
A
C
D

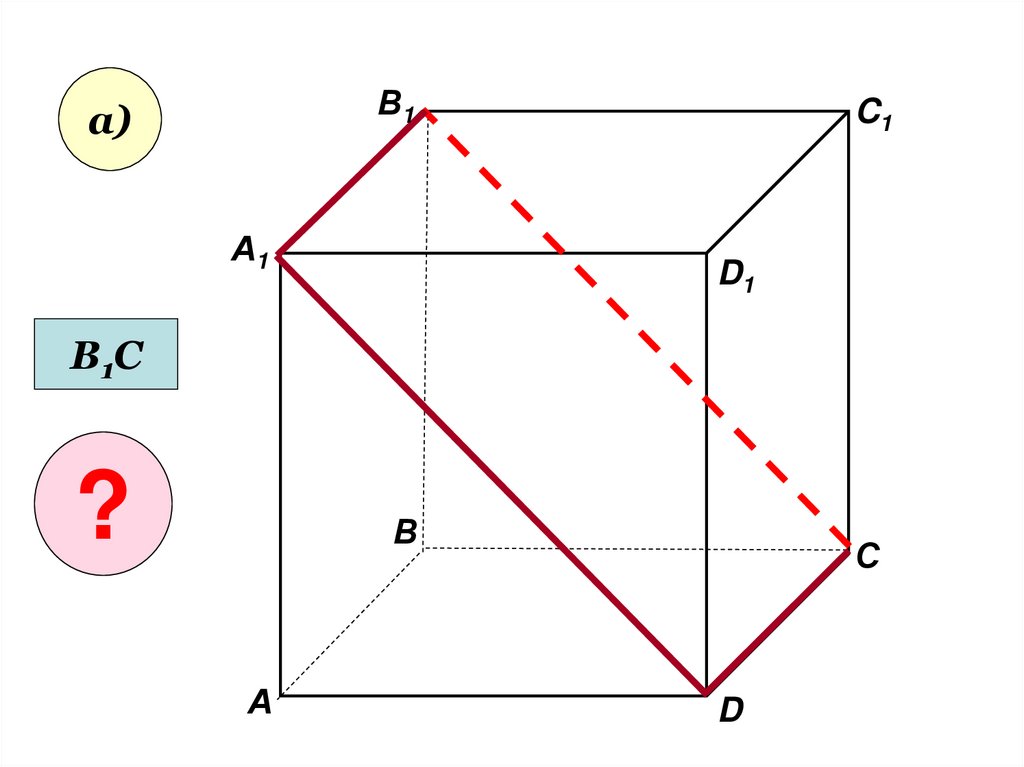
25.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

26.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

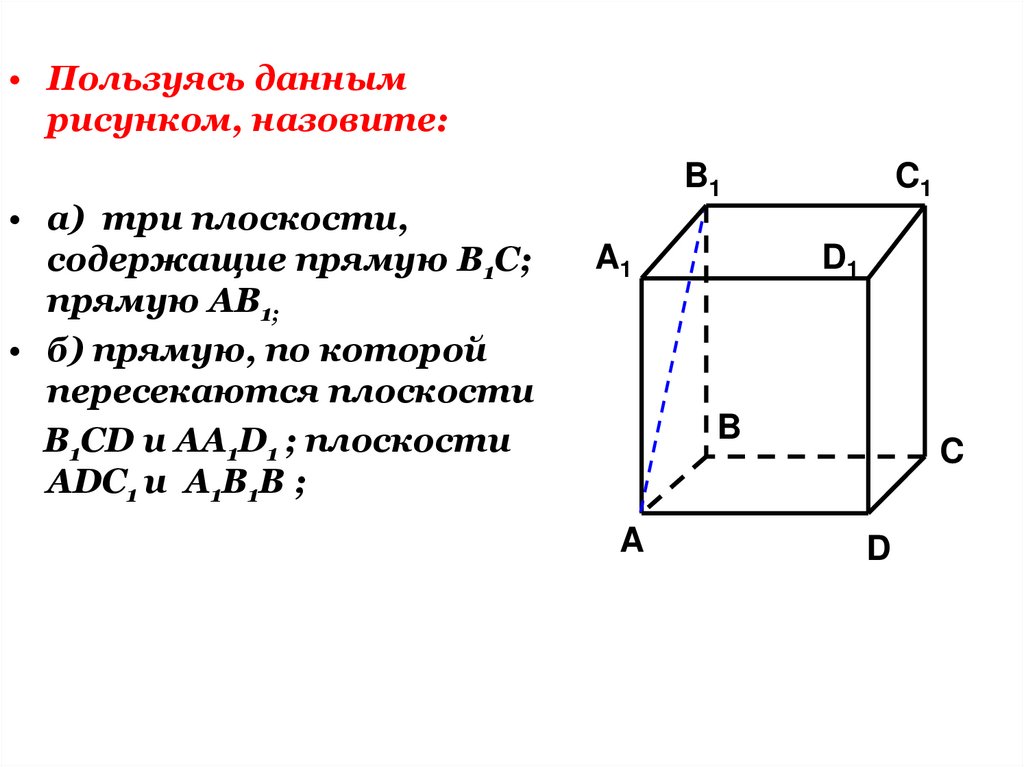
27.

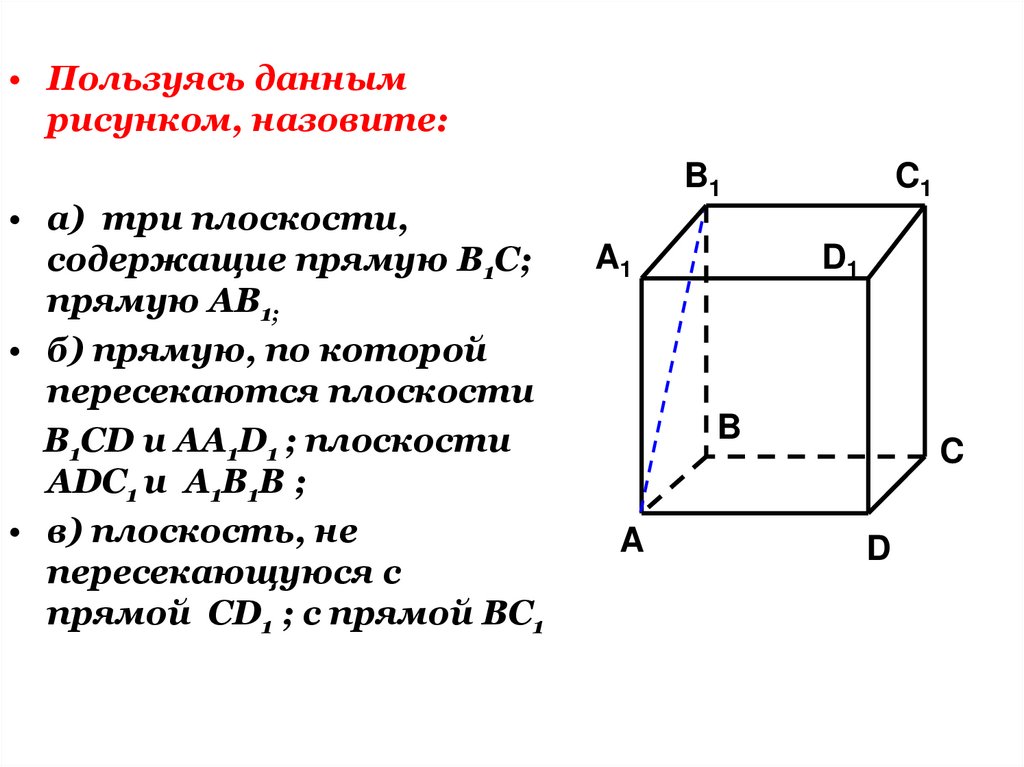
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
B1
A1
C1
D1
B
A
C
D

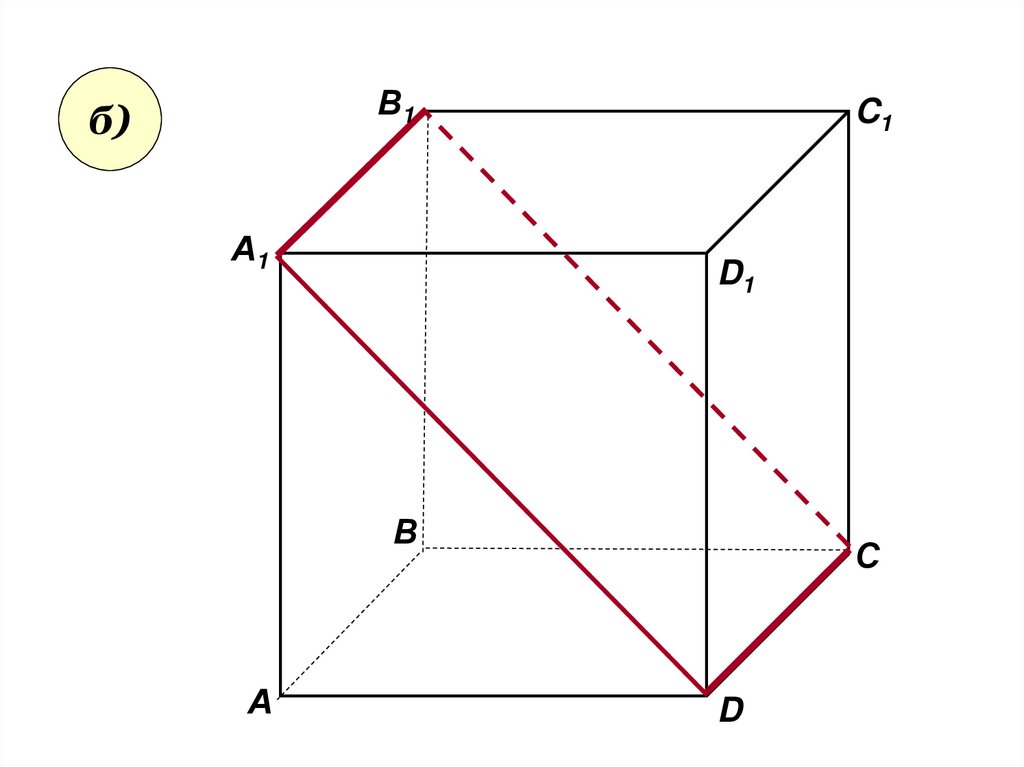
28.

В1
б)
А1
C1
D1
В
А
С
D

29.

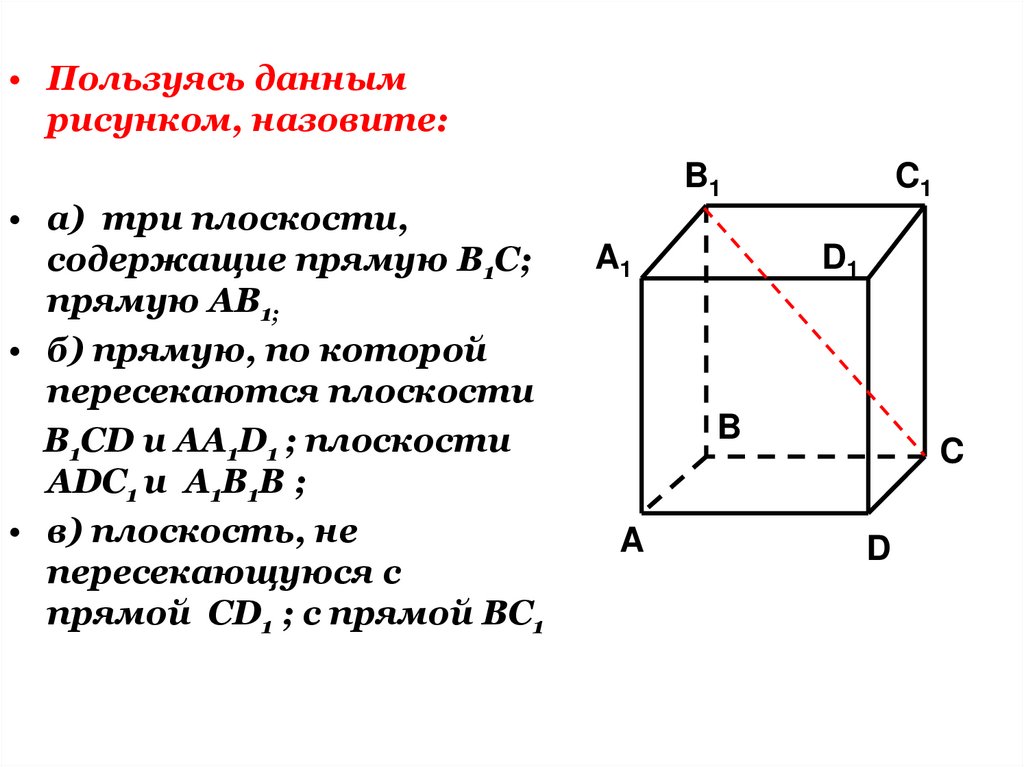
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
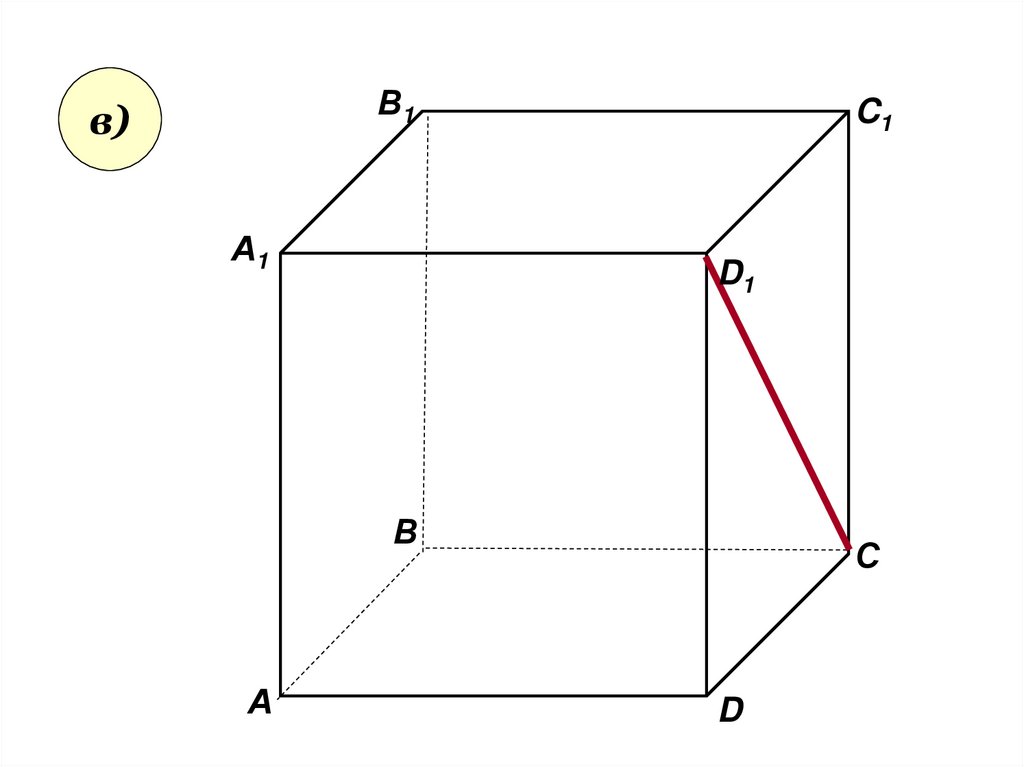
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
A1
C1
D1
B
A
C
D

30.

В1
в)
А1
C1
D1
В
А
С
D

31.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
A1
C1
D1
B
A
C
D

32. Ответьте на вопросы:

• Верно ли, что две прямые параллельны, если они
Нетне
имеют общих точек?
• Верно ли, что если две прямые не Нет
пересекаются, то они параллельны?
• Верно ли, что через две точки можно провести
Да
множество плоскостей?
• Верно ли, что если две прямые лежат в одной
Нет
плоскости, то они параллельны?
• Верно ли, что если две плоскости имеют общую
Да
точку, то они пересекаются по прямой?
• Могут ли две пересекающиеся прямые не лежать в
Да
одной плоскости?

33. Домашнее задание:

1) Выучить аксиомы
и следствия из них.
2) Выучить определения
и теоремы
Успехов!