Предмет стереометрии. Аксиомы стереометрии

1.

2.

Геометрия
Планиметрия
Стереометрия
stereos
телесный, твердый,
объемный,
пространственный

3.

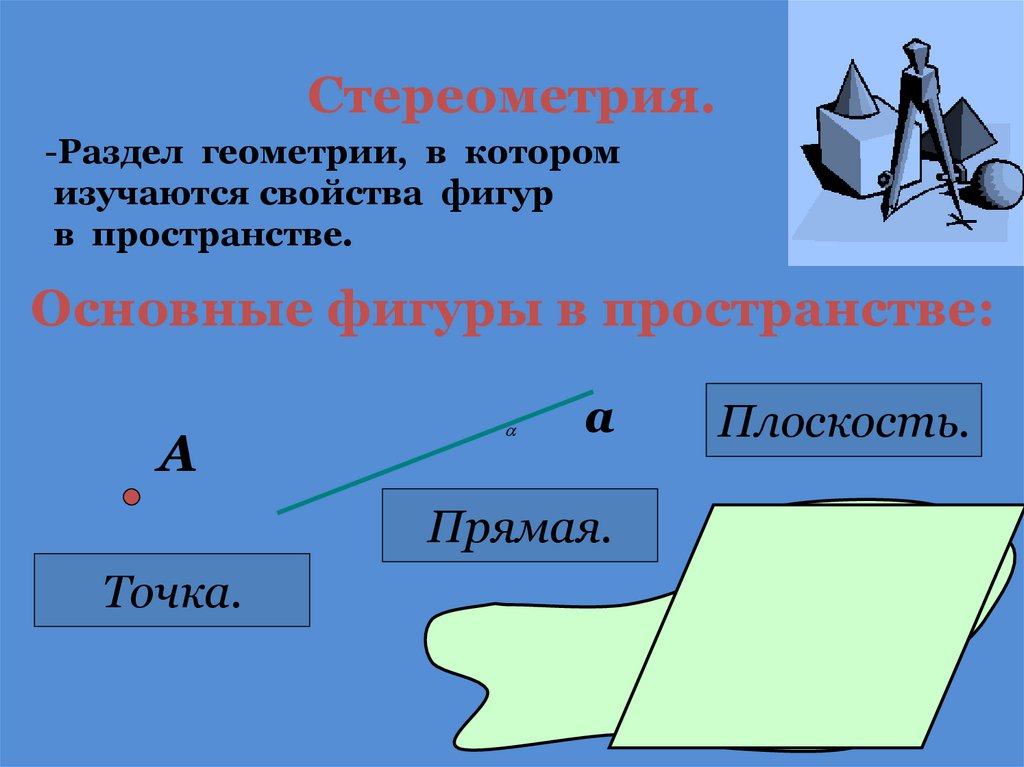
Стереометрия.
-Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Плоскость.
Прямая.

4.

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
, , ,

5.

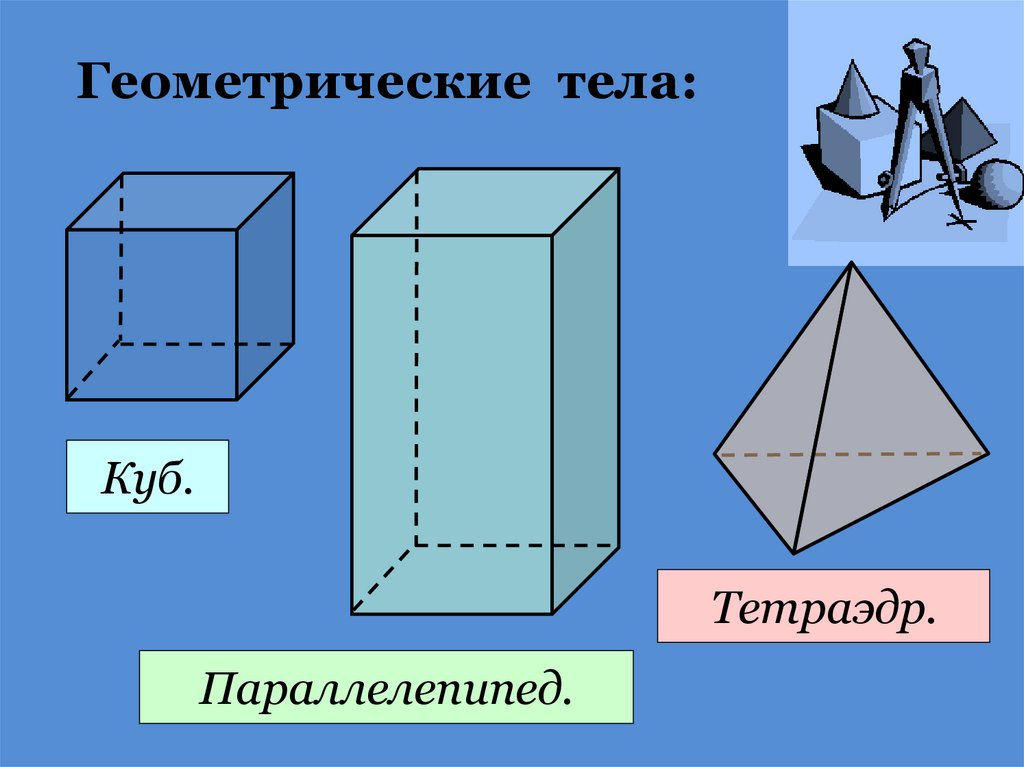
Геометрические тела:
Куб.
Тетраэдр.
Параллелепипед.

6.

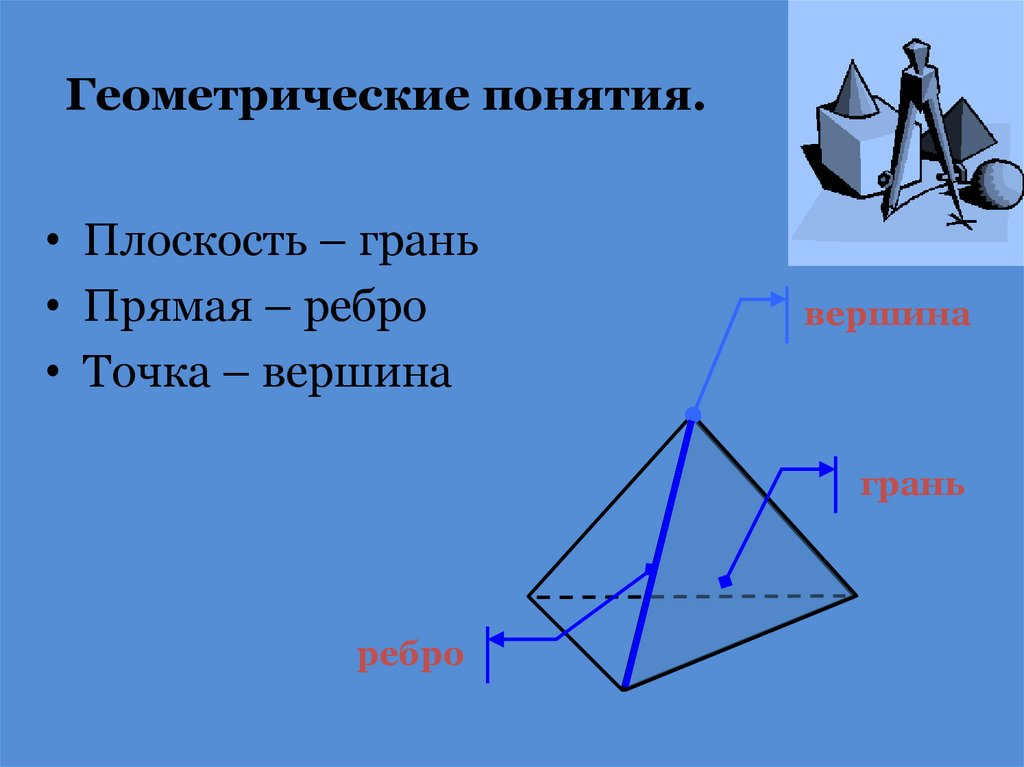
Геометрические понятия.
• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро

7.

Аксиома
(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

8.

АКСИОМЫ
планиметрия
Характеризуют взаимное
расположение точек и прямых
1. Каждой прямой
принадлежат по крайней
мере две точки
2. Имеются по крайней мере
три точки, не лежащие на
одной прямой
3. Через любые две точки
проходит прямая, и притом
только одна.
Основное понятие геометрии
«лежать между»
4. Из трех точек прямой одна и
только одна лежит между двумя
другими.
стереометрия
А1. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
А2. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости
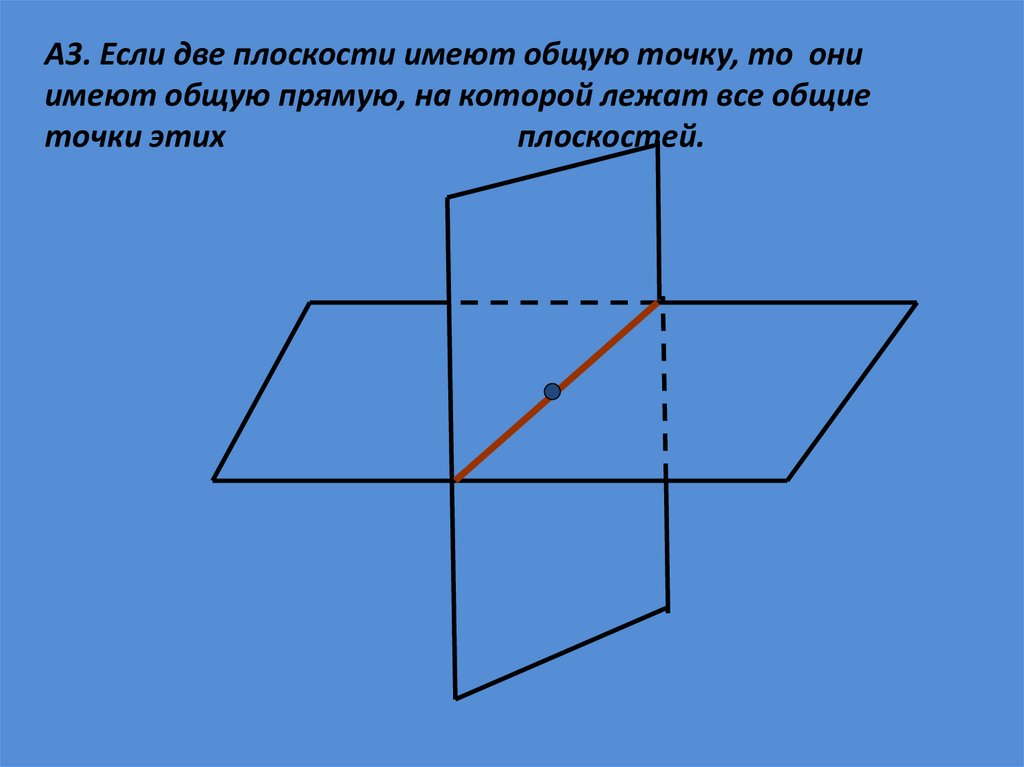
А3. Если две плоскости
имеют общую точку, то они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.

9.

А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих
плоскостей.

10.

Аксиомы стереометрии описывают:
А1.
Способ
задания
плоскости.
А2.
Взаимное
расположение
прямой и
плоскости
А3.
Взаимное
расположение
плоскостей
А
В
А
С
В

11.

Взаимное расположение прямой и плоскости.
Прямая
лежит в
плоскости.
Прямая
пересекает
плоскость.
а
Множество
общих
точек.
а
М
а
Прямая не
пересекает
плоскость.
а
а М
Единственная
общая точка.
а
Нет общих
точек.

12.

Прочти чертёж
С
A
A
C

13.

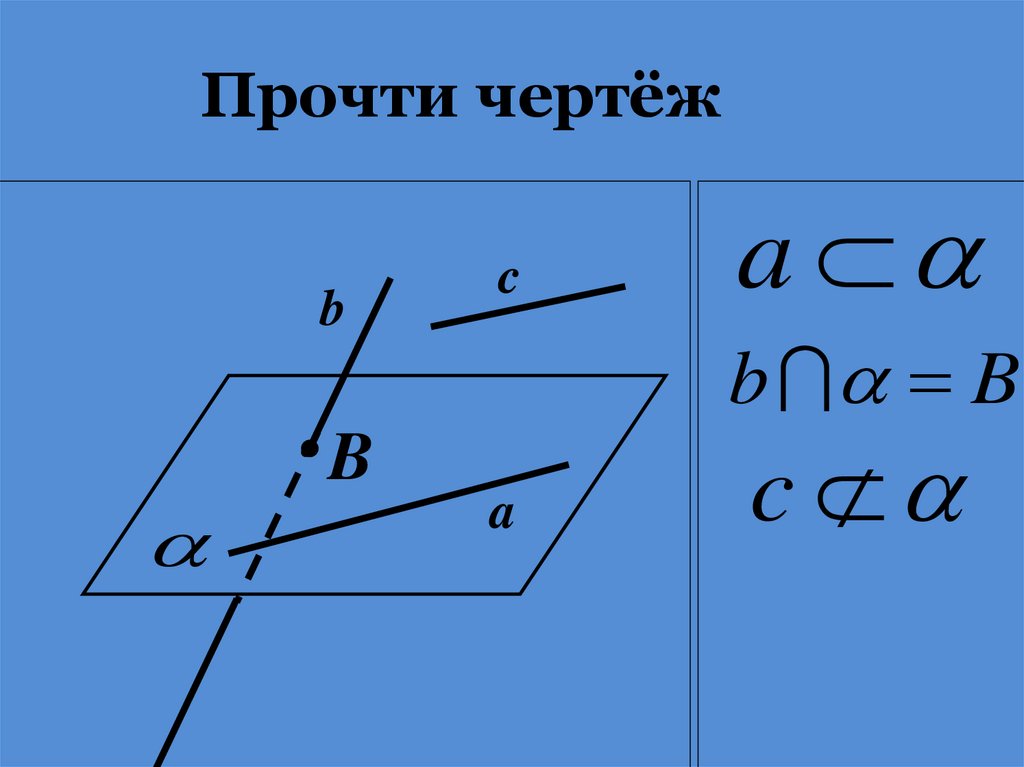
Прочти чертёж
b
B
c
a
b B
a
c

14.

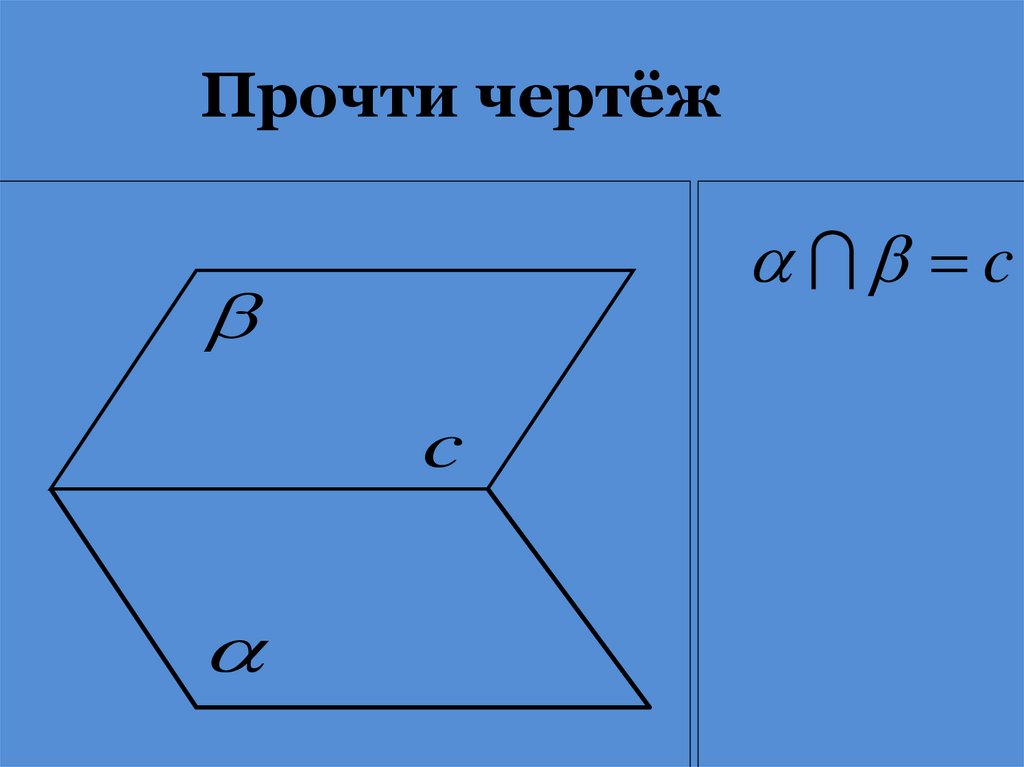
Прочти чертёж
c
c

15.

• Пользуясь данным
рисунком, назовите:
• а) четыре точки,
лежащие в плоскости
SAB, в плоскости АВС;
• б) плоскость, в
которой лежит
прямая MN, прямая
КМ;
• в) прямую, по которой
пересекаются
плоскости ASC и SBC ,
плоскости SAC и CAB.
S
К
C
А
М
N
В

16.

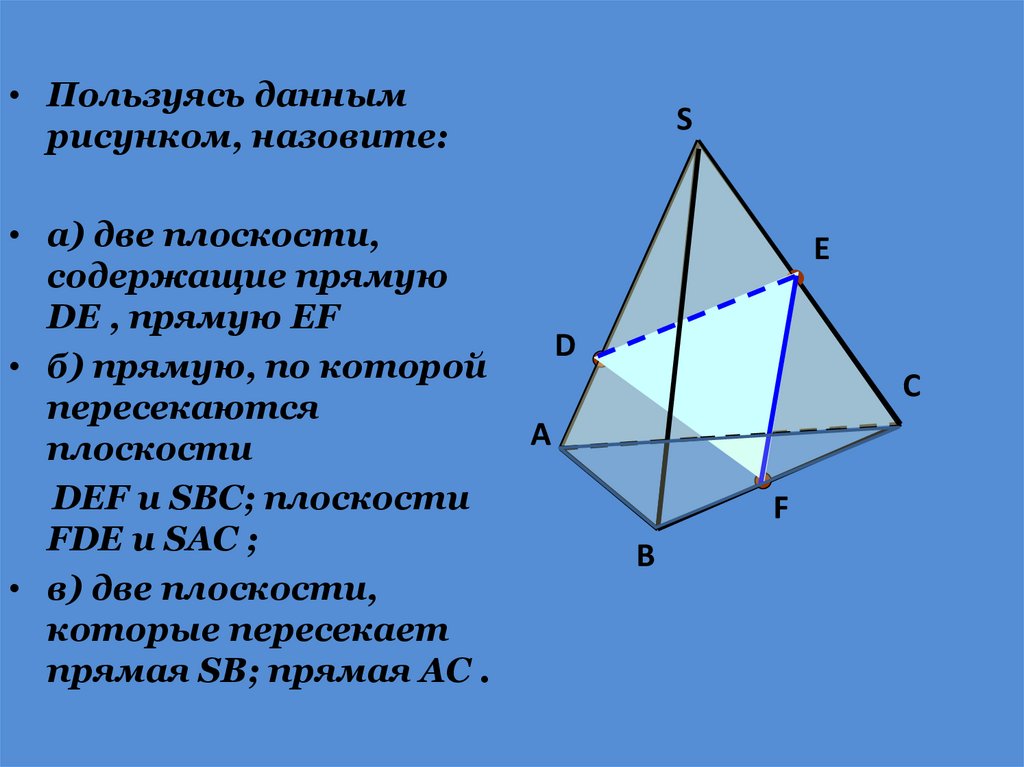
• Пользуясь данным
рисунком, назовите:
• а) две плоскости,
содержащие прямую
DE , прямую EF
• б) прямую, по которой
пересекаются
плоскости
DEF и SBC; плоскости
FDE и SAC ;
• в) две плоскости,
которые пересекает
прямая SB; прямая AC .
S
E
D
С
А
F
В

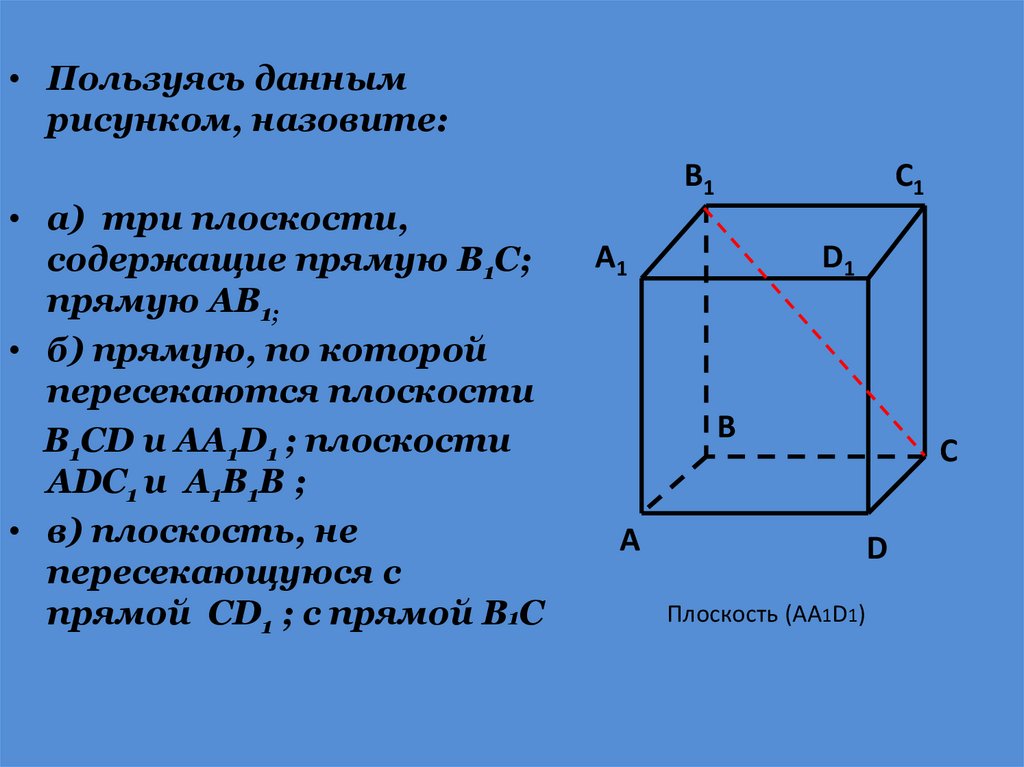
17.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
B1
C1
A1
D1
B
A
C
D

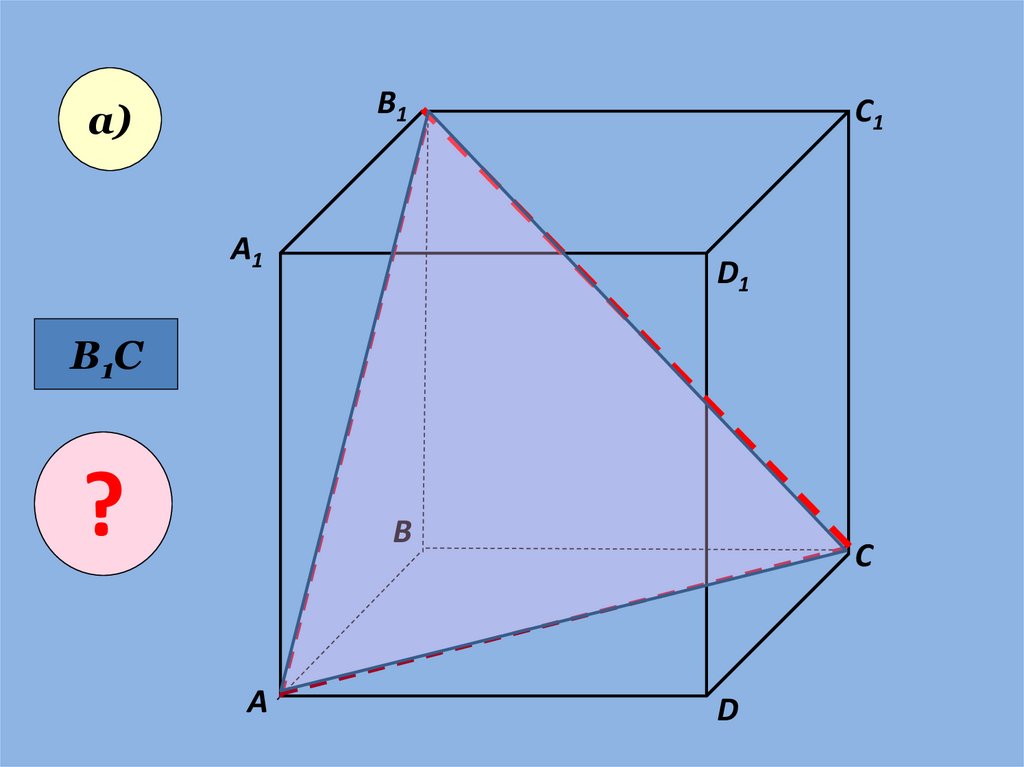
18.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

19.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

20.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

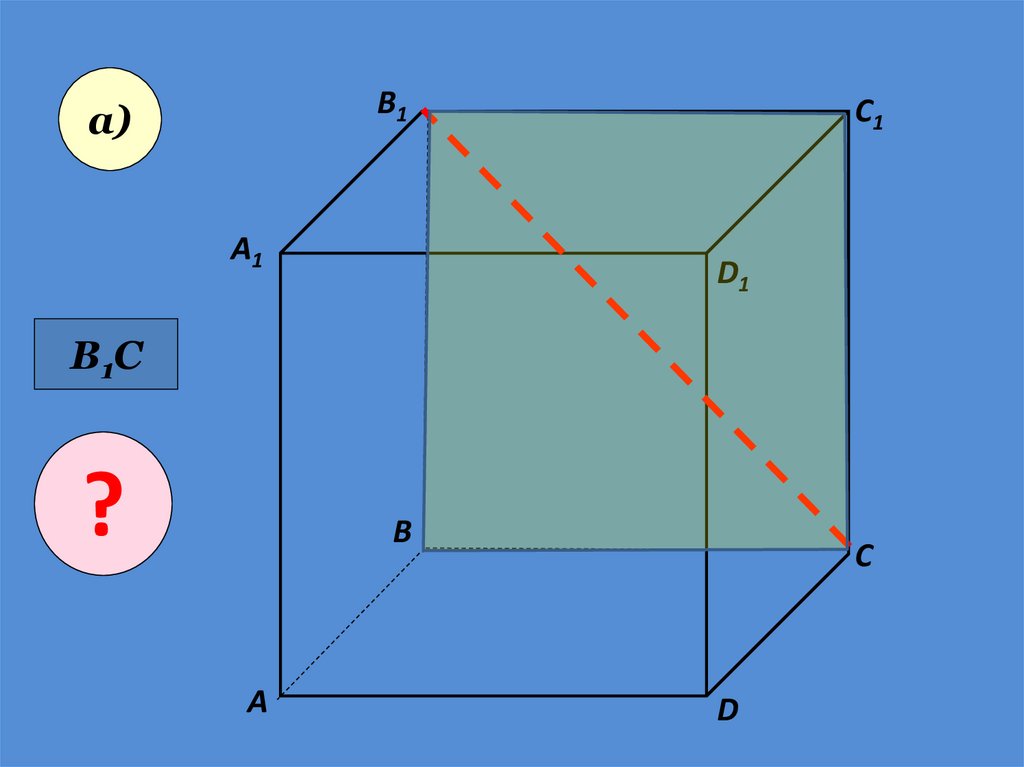
21.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
B1
C1
A1
D1
B
A
C
D
Плоскости: (АА1В1), (АВ1С), (АВ1С1)

22.

В1
б)
А1
C1
D1
В
А
С
D

23.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с прямой
CD1 ; с прямой B1C.
B1
C1
A1
D1
B
A
C
D

24.

В1
в)
А1
C1
D1
В
А
С
D

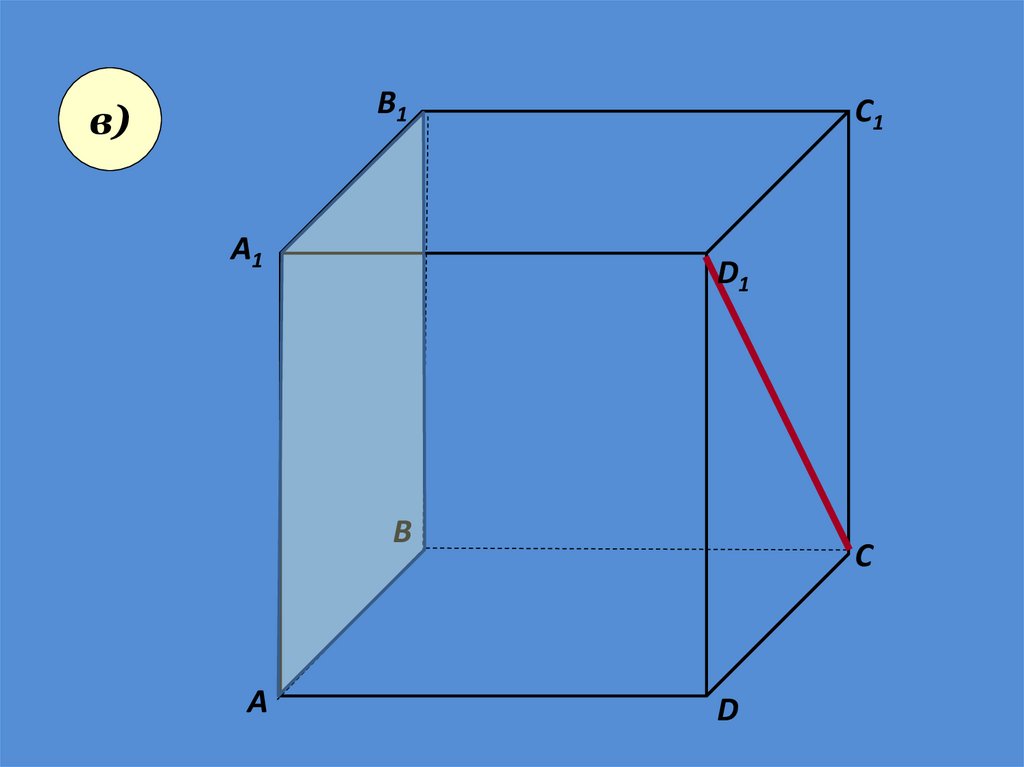
25.

• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой B1C
B1
C1
A1
D1
B
A
C
D
Плоскость (АА1D1)