Similar presentations:
Введение в стереометрию. Аксиомы стереометрии, следствия из них
1. Уважаемые студенты 1м группы! Мы переходим на дистанционный формат изучения математики. Не волнуйтесь, у вас все получится! .
Внимательно читайте комментарии к каждому занятию.Четко следуйте инструкции к каждому заданию.
Все материалы, которые необходимо будет прислать в
электронном формате, высылайте ТОЛЬКО на электронную
почту Sobkoolgavasilivna@mail.ru
Желаю успехов!
2.
Практическое занятие по теме:Введение в стереометрию. Аксиомы стереометрии, следствия из
них.
Цели занятия: повторить изученные аксиомы о взаимном расположении
точек, прямых и плоскостей в пространстве; показать применение аксиом к
решению задач; сформировать навык применения аксиом стереометрии и
их следствий при решении задач.
План занятия
1. Актуализация опорных знаний
• Основные понятия стереометрии.
• Аксиомы стереометрии.
• Некоторые следствия из аксиом.
2. Решение задач на применение аксиом стереометрии и их
следствий
3.
• На слайдах 4-34 представлен теоретическийматериал, изученный нами па предыдущем
занятии.
• Повторите его (конспектировать не нужно!!!).
• Используйте теоретический материал при
выполнении практических заданий.
• Фотоотчет выполнения практического занятия
и домашнего задания присылать до 30.10.21г.
на электронный адрес
Sobkoolgavasilivna@mail.ru с пометкой
«Домашнее задание от 27.09.21»
4.
ПланиметрияСтереометрия
Изучает свойства
геометрических фигур
на плоскости
Изучает свойства фигур
в пространстве
В переводе с греческого
слово «геометрия»
означает «землемерие»
«гео» – по-гречески
земля, «метрео» –
мерить
Слово «стереометрия»
происходит от греческих
слов «стереос» объемный,
пространственный,
«метрео» – мерить
5.
ПланиметрияСтереометрия
Основные фигуры:
точка, прямая
Основные фигуры: точка,
прямая, плоскость
Другие фигуры: отрезок,
луч, треугольник,
квадрат, ромб,
параллелограмм,
трапеция, прямоугольник,
выпуклые и невыпуклые
n-угольники, круг,
окружность, дуга и др.
Наряду с этими фигурами
мы будем рассматривать
геометрические тела и их
поверхности.
Например, многогранники.
Куб, параллелепипед,
призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр,
конус.
6. Стереометрия -
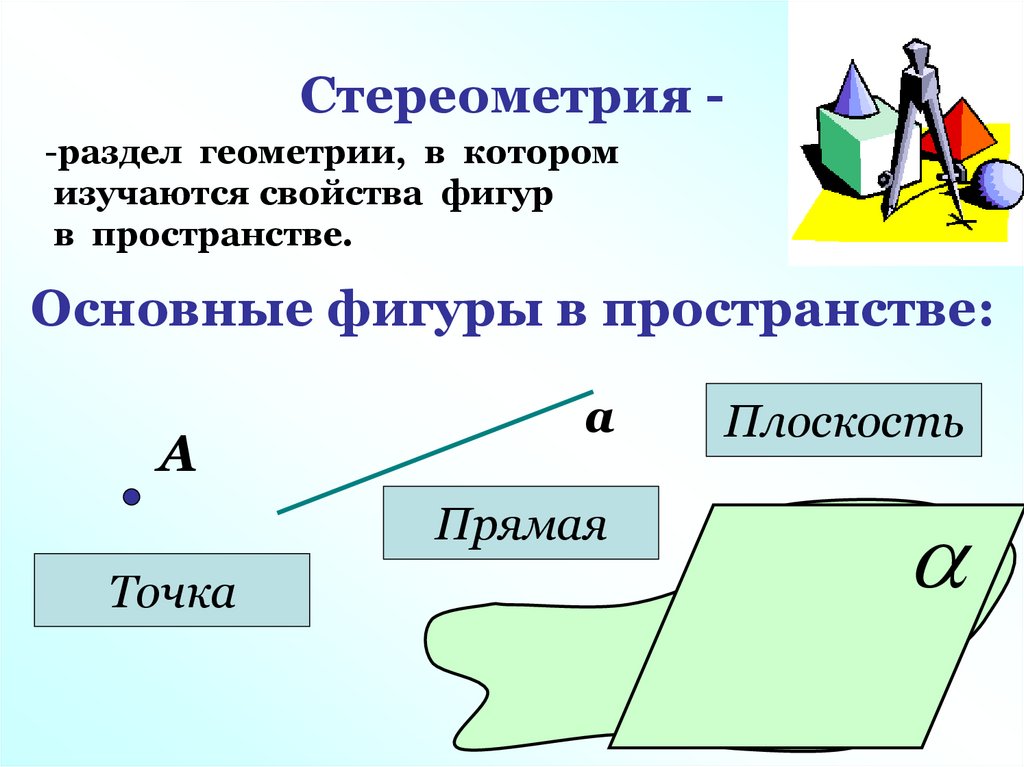
Стереометрия -раздел геометрии, в которомизучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка
а
Плоскость
Прямая
7.
A, B, C, …a, b, c, …
или
AВ, BС, CD, …
, , ,
8.
Плоскости будем обозначать греческими буквами.На рисунках плоскости обозначаются в виде
параллелограммов. Плоскость как геометрическую
фигуру следует представлять себе простирающейся
неограниченно во все стороны.
9.
Стереометрия широко используется встроительном деле, архитектуре, машиностроении,
геодезии, во многих других областях науки и техники.
При
проектировании
этой машины
важно было получить такую форму, чтобы при
движении сопротивление воздуха было минимально.
10.
Оперный театр в СиднееДатский архитектор Йорн Утцон был
вдохновлён видом парусов.
11.
Эйфелева башняПариж, Марсово поле
Инженер Гюстав
Эйфель нашел
необычную форму для
своего проекта.
Эйфелева башня
весьма устройчива:
сильный ветер
отклоняет ее вершину
всего лишь на 10-12 см.
В жару от
неравномерного
нагревания
солнечными лучами
она может отклониться
на 18 см.
12.
18000 железных деталей скрепляются 2500000заклёпками
13.
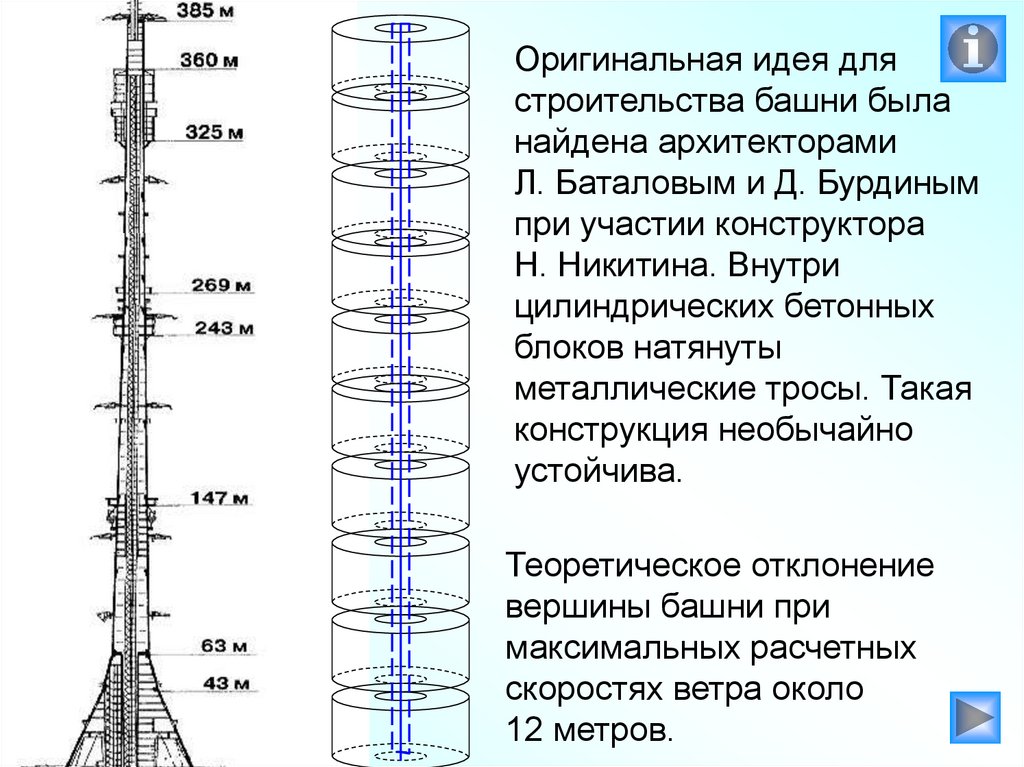
Оригинальная идея длястроительства башни была
найдена архитекторами
Л. Баталовым и Д. Бурдиным
при участии конструктора
Н. Никитина. Внутри
цилиндрических бетонных
блоков натянуты
металлические тросы. Такая
конструкция необычайно
устойчива.
Теоретическое отклонение
вершины башни при
максимальных расчетных
скоростях ветра около
12 метров.
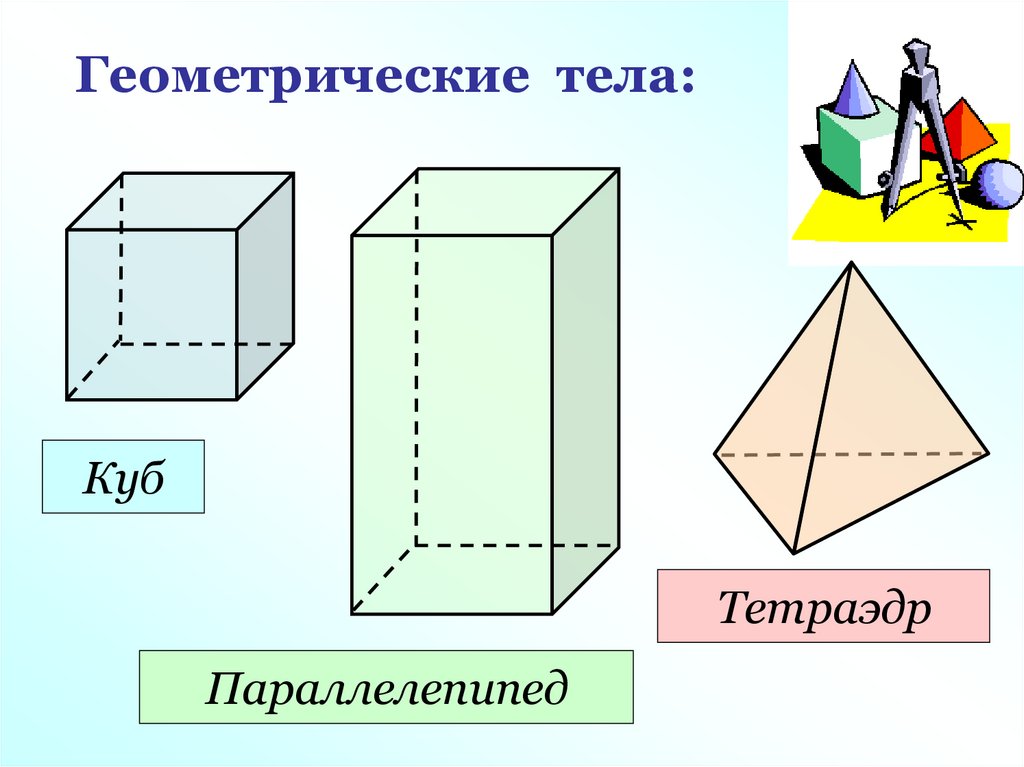
14. Геометрические тела:
КубТетраэдр
Параллелепипед
15. Геометрические понятия
Аксиома(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства
16. Аксиома
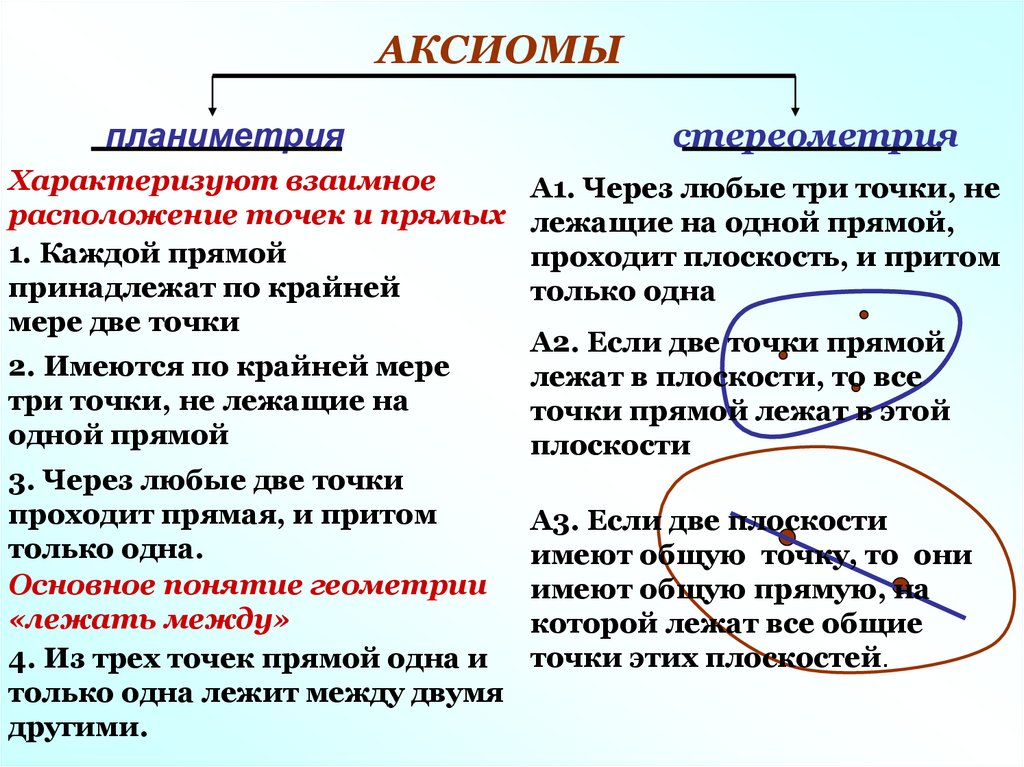
АКСИОМЫпланиметрия
Характеризуют взаимное
расположение точек и прямых
1. Каждой прямой
принадлежат по крайней
мере две точки
стереометрия
А1. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
2. Имеются по крайней мере
три точки, не лежащие на
одной прямой
А2. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости
3. Через любые две точки
проходит прямая, и притом
только одна.
Основное понятие геометрии
«лежать между»
4. Из трех точек прямой одна и
только одна лежит между двумя
другими.
А3. Если две плоскости
имеют общую точку, то они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.
17.
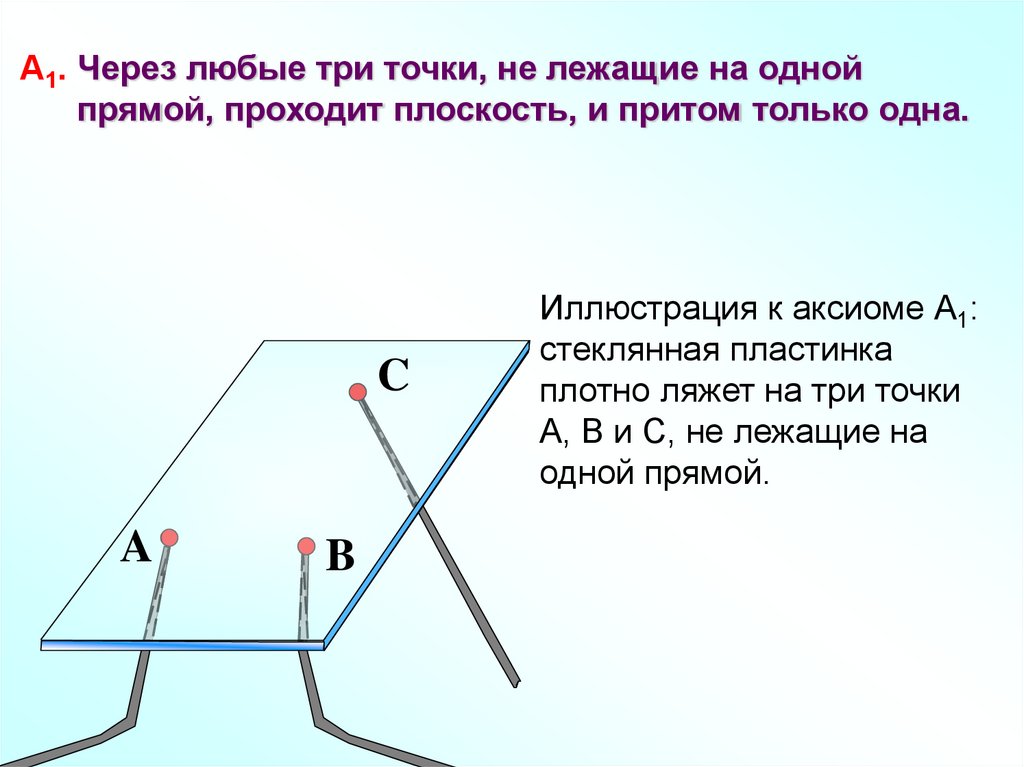
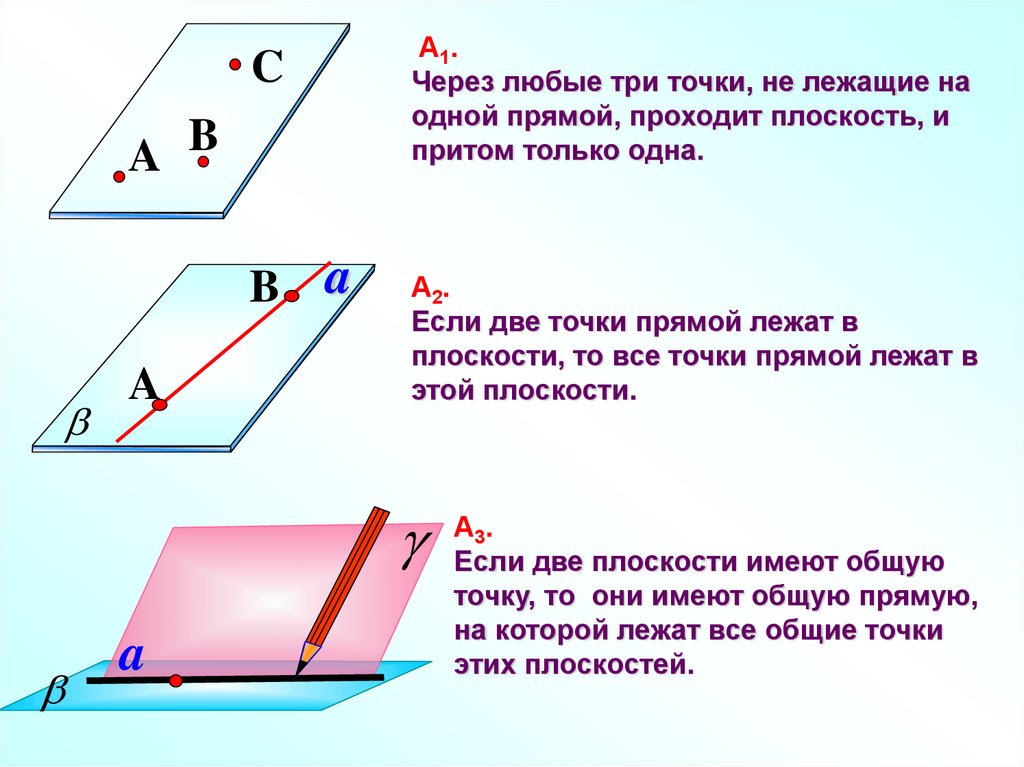
А1. Через любые три точки, не лежащие на однойпрямой, проходит плоскость, и притом только одна.
C
A
B
Иллюстрация к аксиоме А1:
стеклянная пластинка
плотно ляжет на три точки
А, В и С, не лежащие на
одной прямой.
18.
Иллюстрации к аксиоме А1 из жизни19.
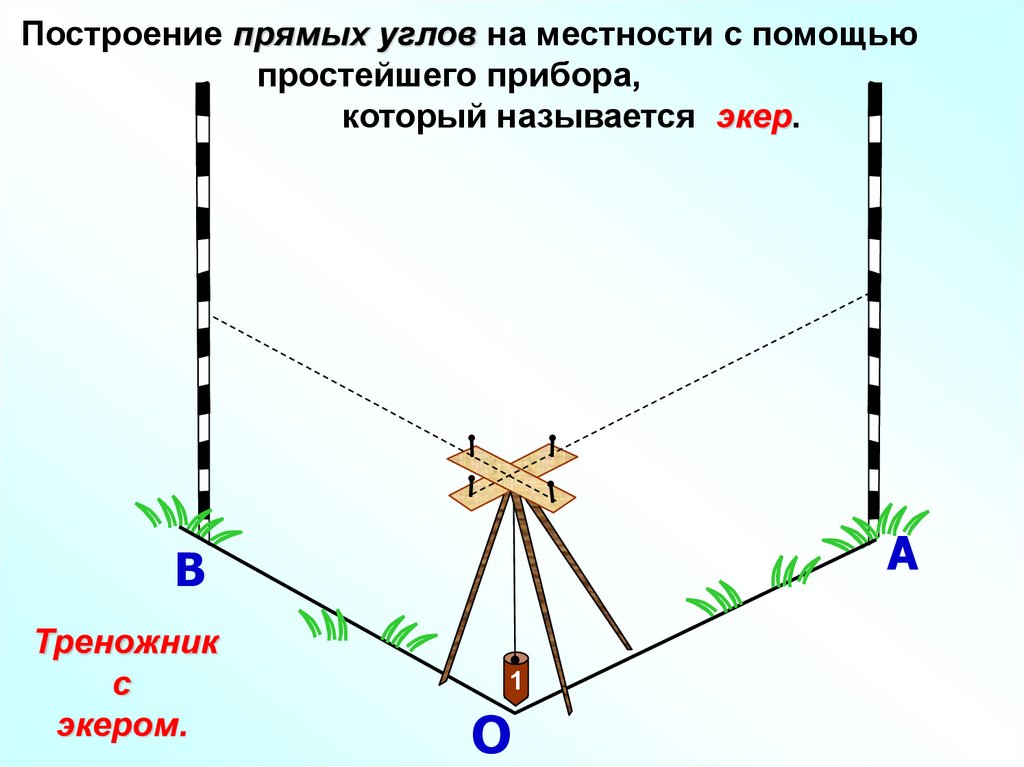
Построение прямых углов на местности с помощьюпростейшего прибора,
который называется экер.
А
В
Треножник
с
экером.
1
О
20.
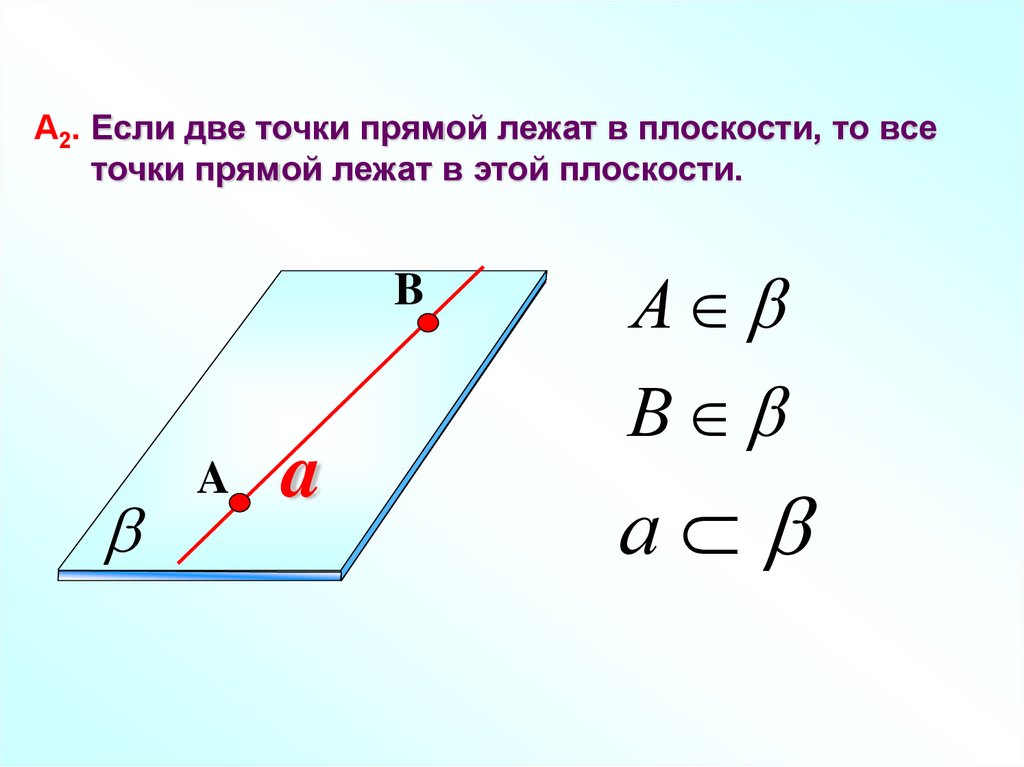
А2. Если две точки прямой лежат в плоскости, то всеточки прямой лежат в этой плоскости.
B
A
a
А
В
а
21.
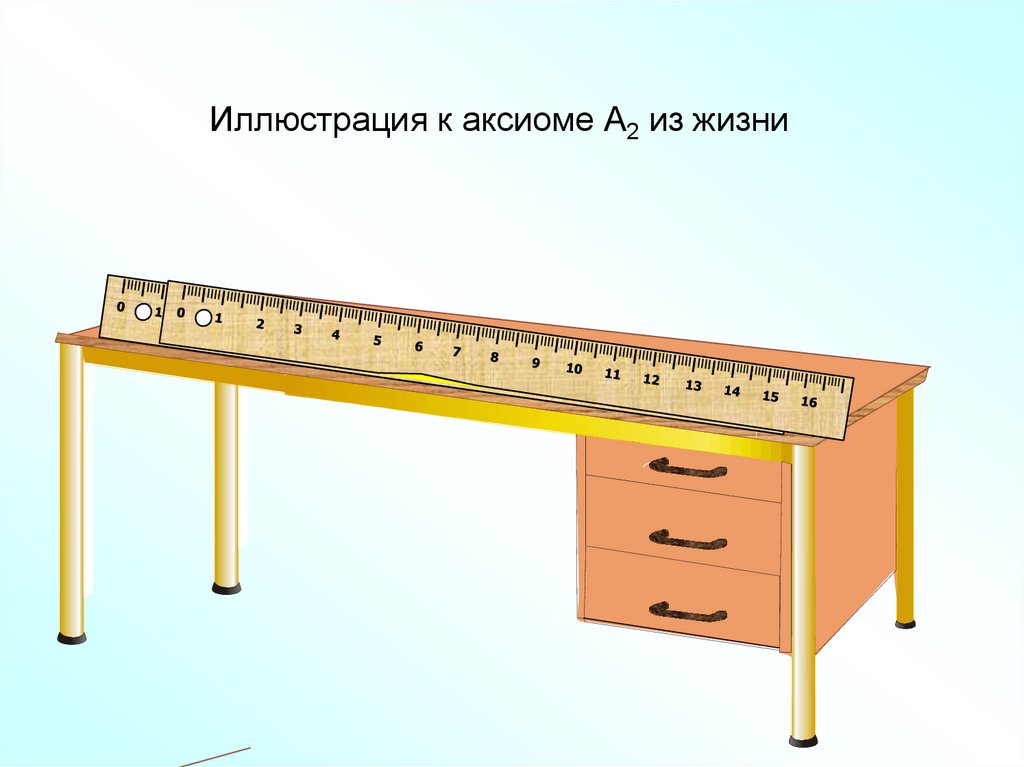
Иллюстрация к аксиоме А2 из жизни22.
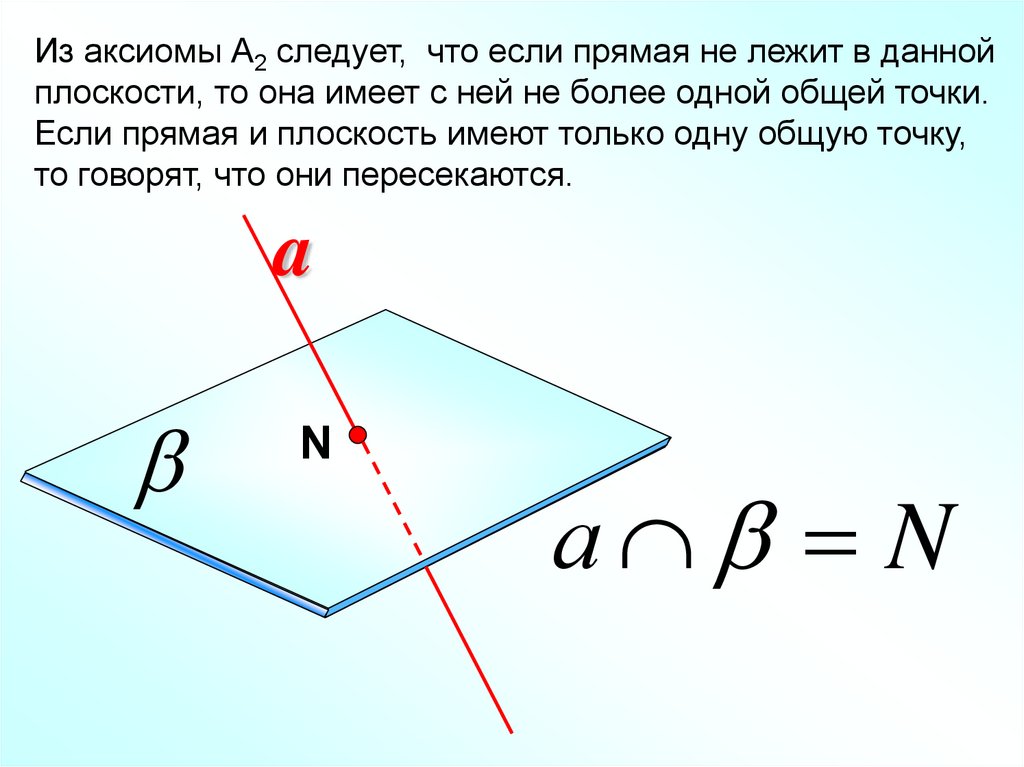
Из аксиомы А2 следует, что если прямая не лежит в даннойплоскости, то она имеет с ней не более одной общей точки.
Если прямая и плоскость имеют только одну общую точку,
то говорят, что они пересекаются.
a
N
а N
23.
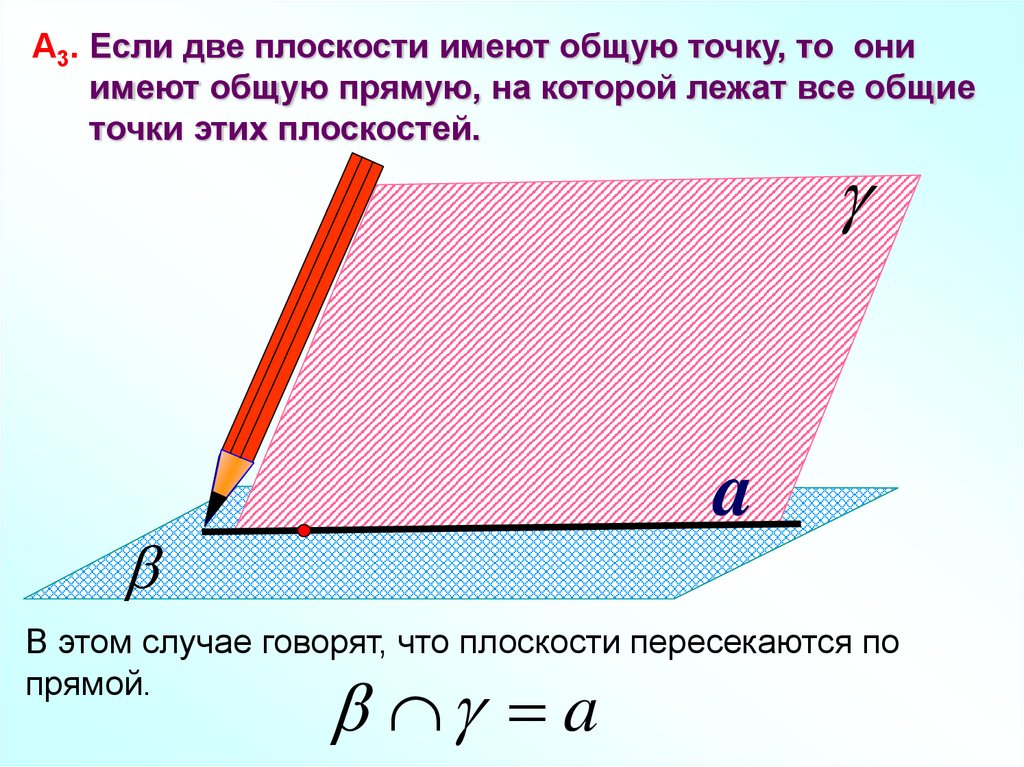
А3. Если две плоскости имеют общую точку, то ониимеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
В этом случае говорят, что плоскости пересекаются по
прямой.
a
24.
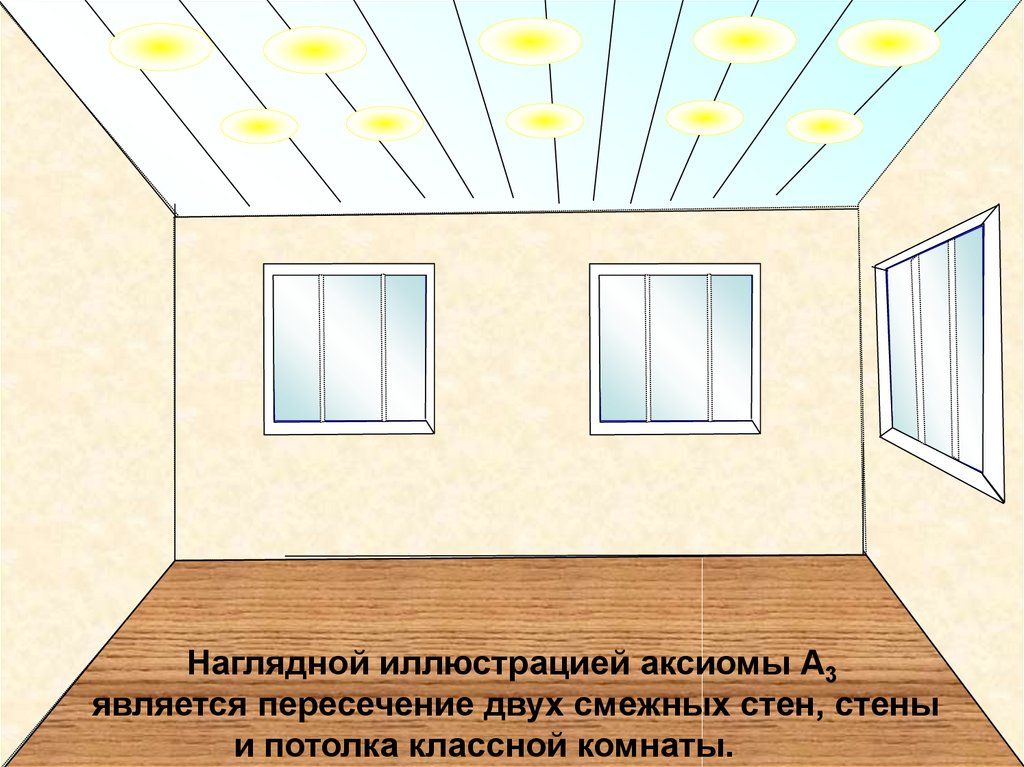
Наглядной иллюстрацией аксиомы А3является пересечение двух смежных стен, стены
и потолка классной комнаты.
25.
CB
A
B a
A
А 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 2.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 3.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.
26.
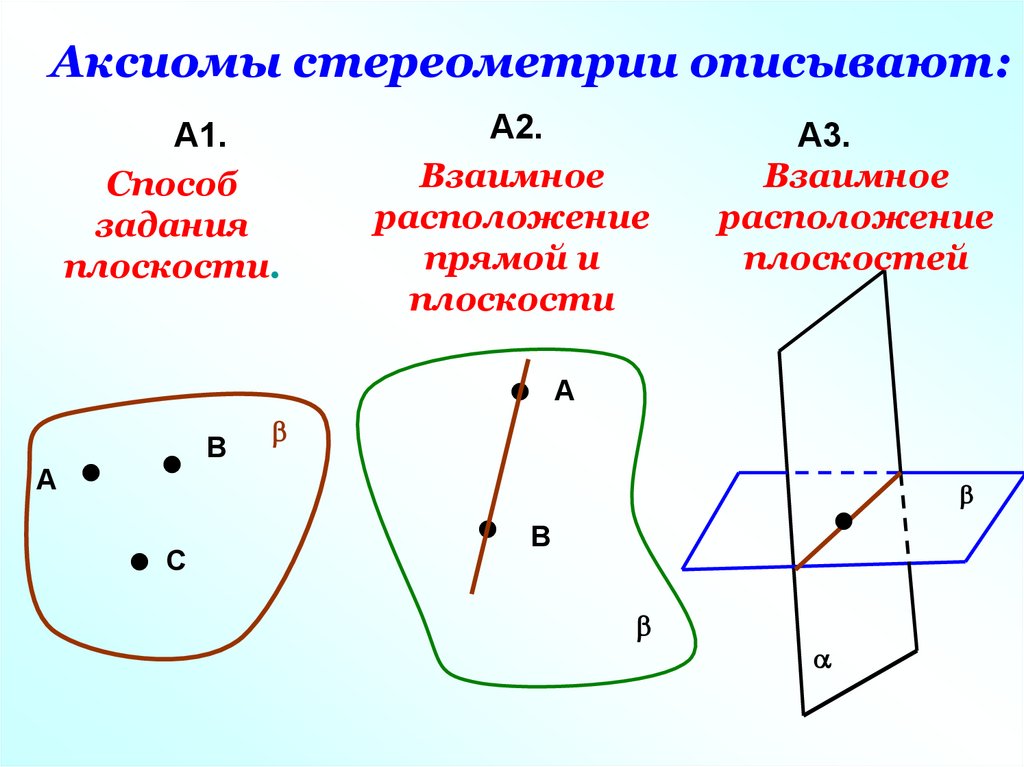
Аксиомы стереометрии описывают:А1.
Способ
задания
плоскости.
А2.
Взаимное
расположение
прямой и
плоскости
А3.
Взаимное
расположение
плоскостей
А
В
А
С
В
27.
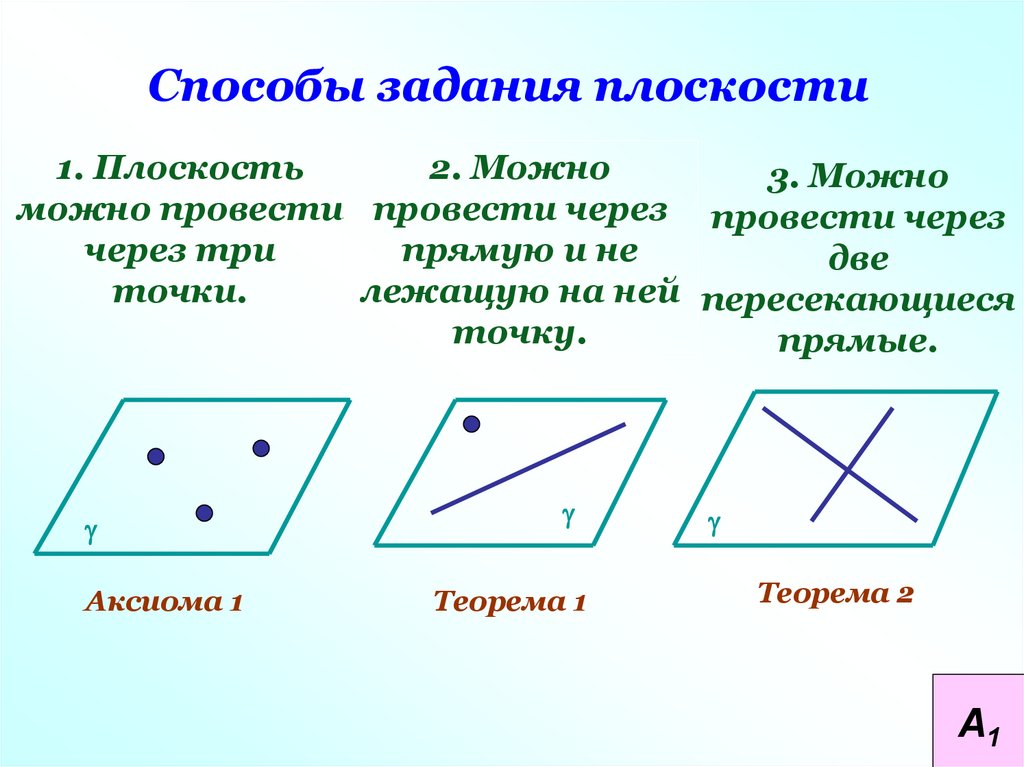
Способы задания плоскости1. Плоскость
2. Можно
3. Можно
можно провести провести через провести через
через три
прямую и не
две
точки.
лежащую на ней пересекающиеся
точку.
прямые.
Аксиома 1
Теорема 1
Теорема 2
А1
28.
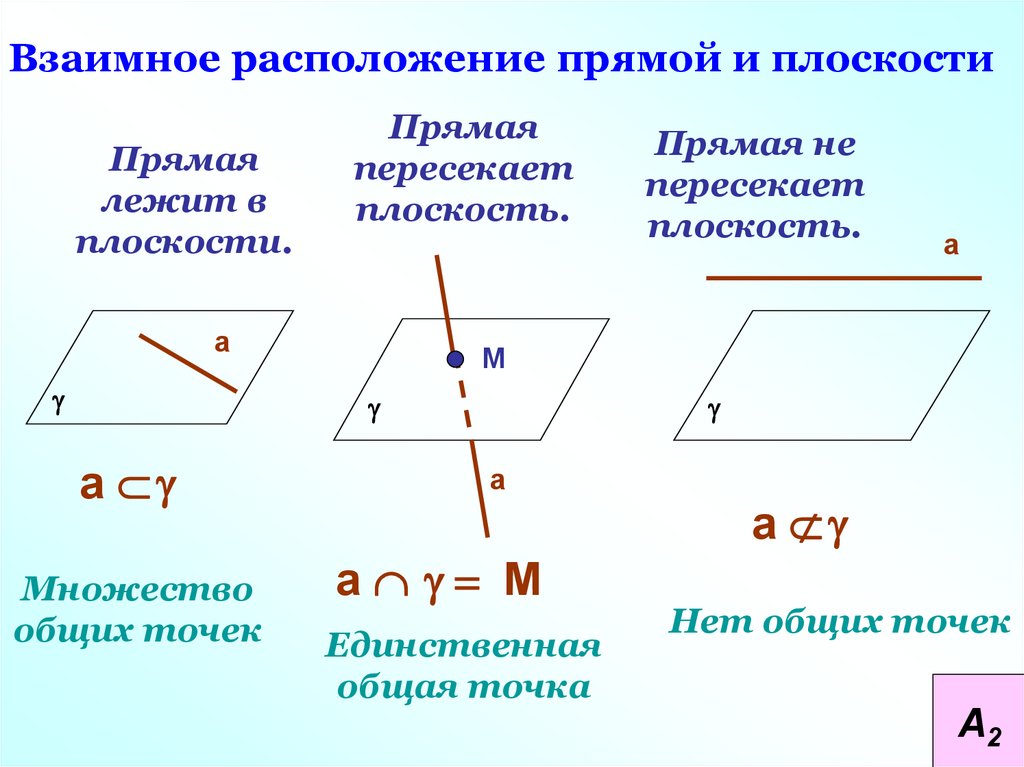
Взаимное расположение прямой и плоскостиПрямая
лежит в
плоскости.
Прямая
пересекает
плоскость.
а
Множество
общих точек
а
М
а
Прямая не
пересекает
плоскость.
а
а М
Единственная
общая точка
а
Нет общих точек
А2
29.
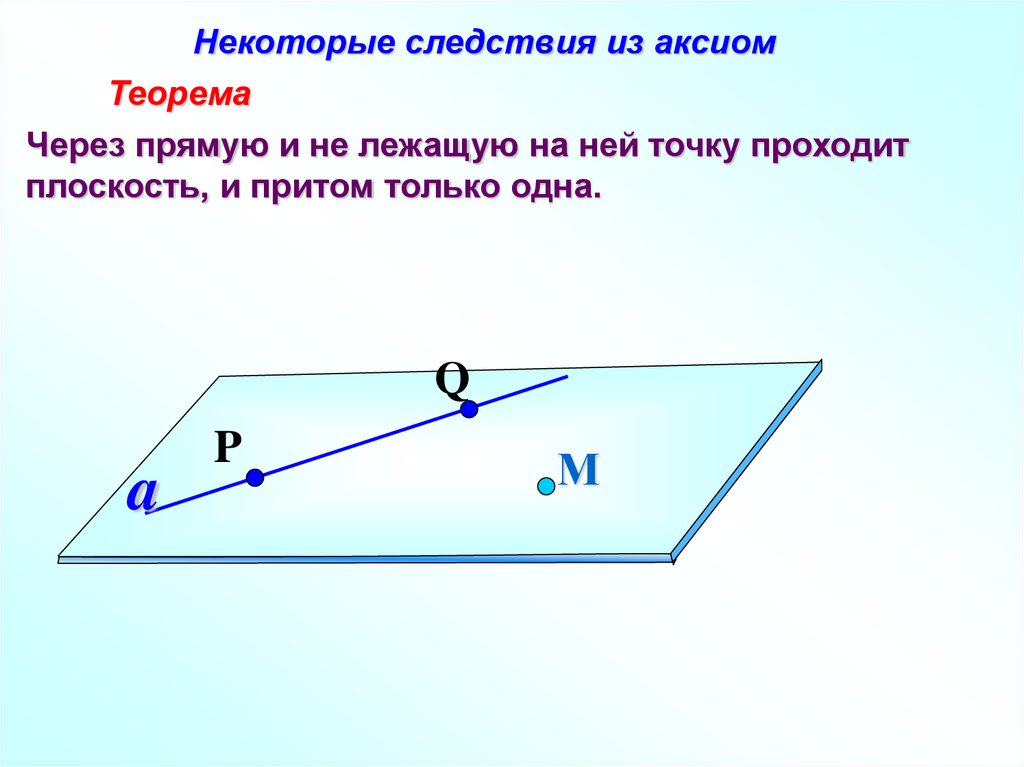
Некоторые следствия из аксиомТеорема
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М
30.
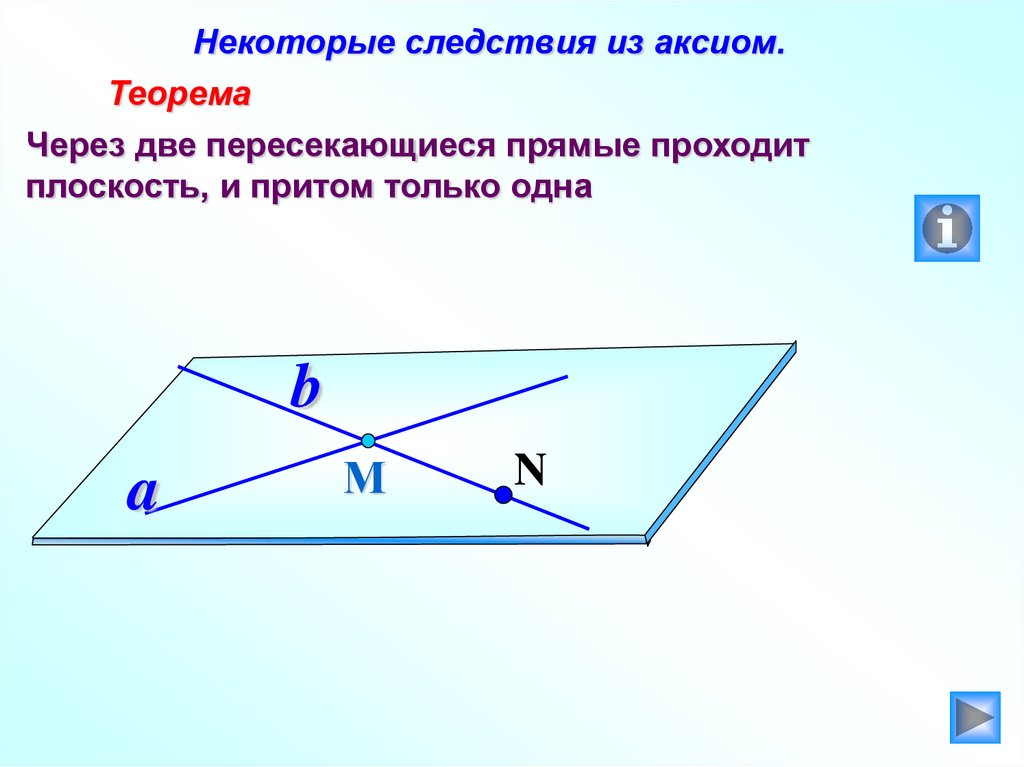
Некоторые следствия из аксиом.Теорема
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N
31.
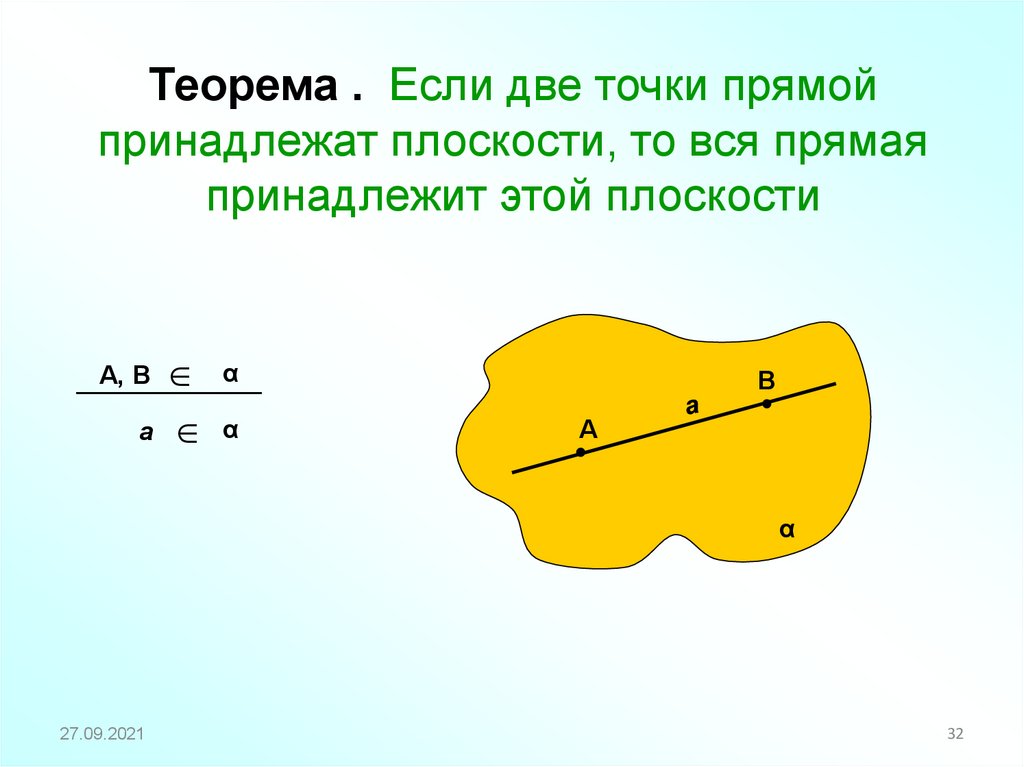
Теорема . Если две точки прямойпринадлежат плоскости, то вся прямая
принадлежит этой плоскости
А, В α
_____________
а
α
В
А
α
27.09.2021
32
32. Теорема . Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости
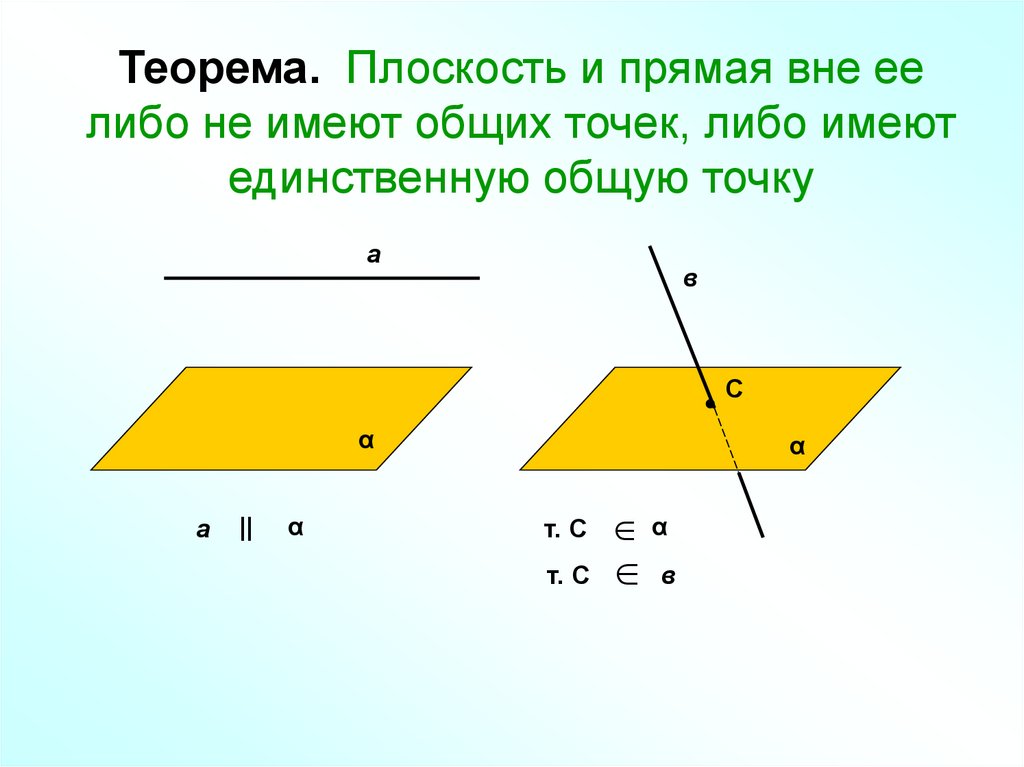
Теорема. Плоскость и прямая вне еелибо не имеют общих точек, либо имеют
единственную общую точку
а
в
С
α
а
||
α
α
т. С
т. С
α
в
33. Теорема. Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку
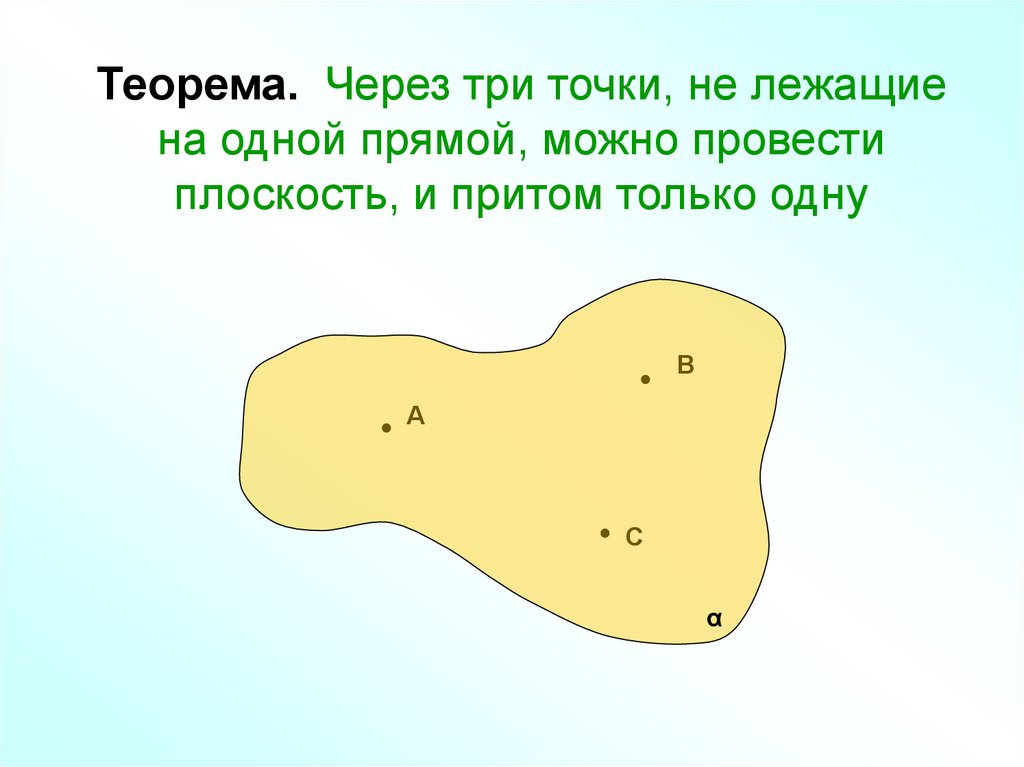
Теорема. Через три точки, не лежащиена одной прямой, можно провести
плоскость, и притом только одну
В
А
С
α
34. Теорема. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну
Практическое выполнениезаданий
• Следующие задания выполнить
письменно в лекционно-практической
тетради.
• Поставить дату проведения занятия,
написать тему занятия.
• При выполнении заданий в тетради
делать записи «Слайд № 36» и т.д.
35. Практическое выполнение заданий
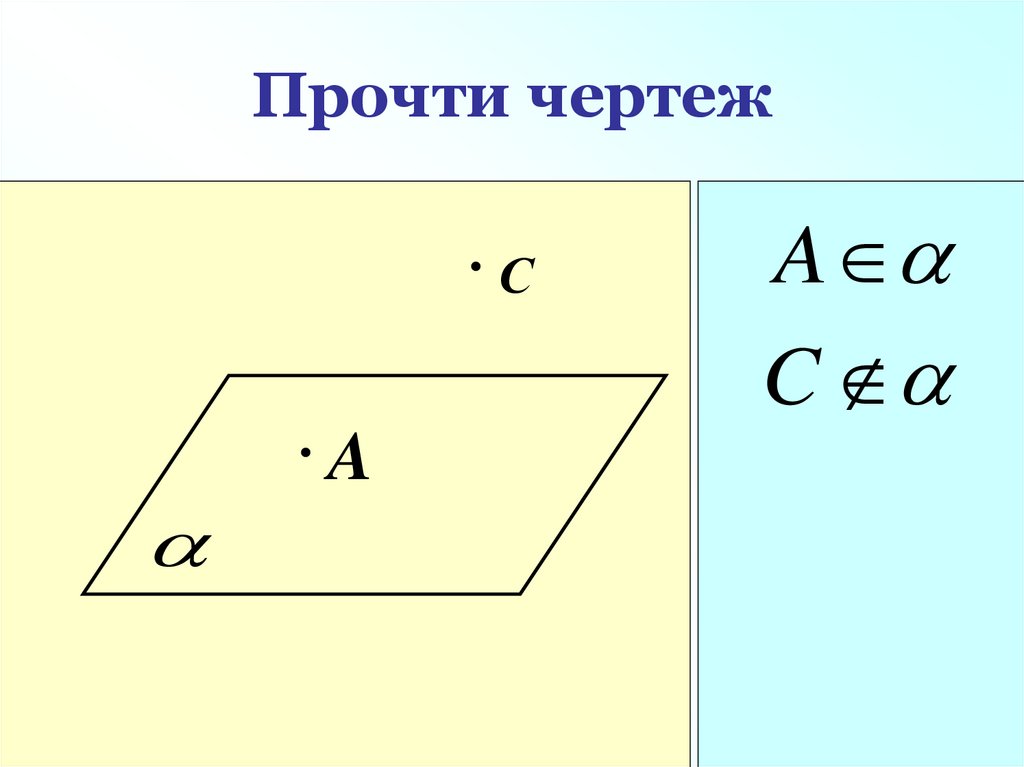
Прочти чертежС
A
A
C
36. Прочти чертеж
bB
c
a
b B
a
c
37. Прочти чертеж
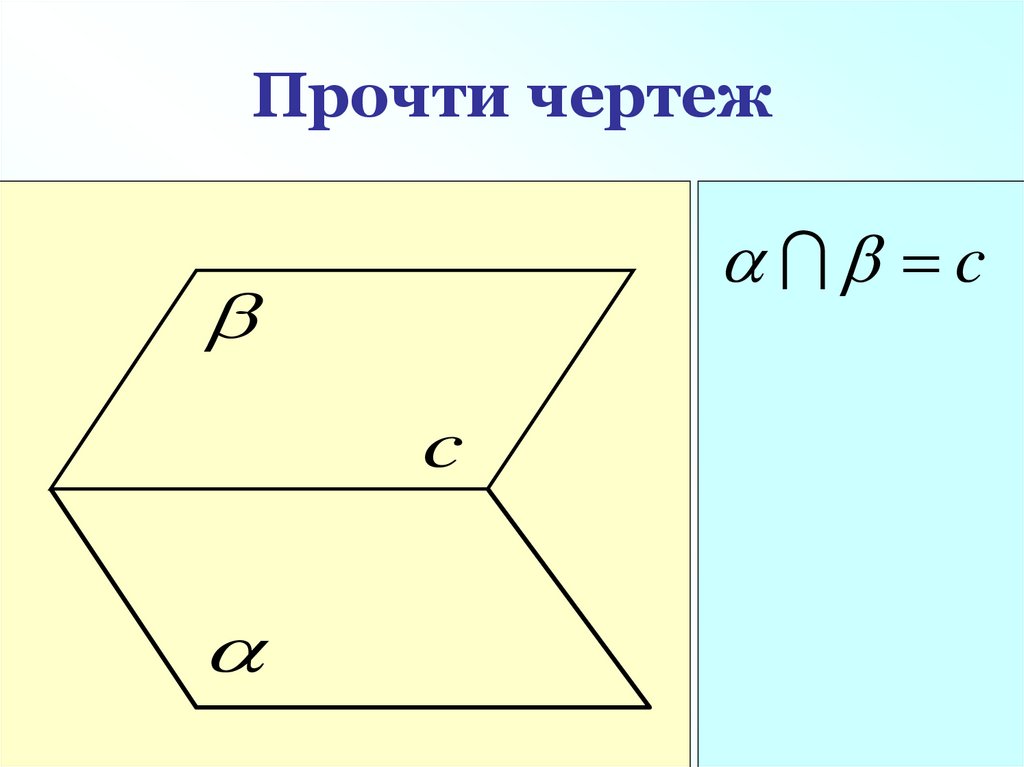
cc
38. Прочти чертеж
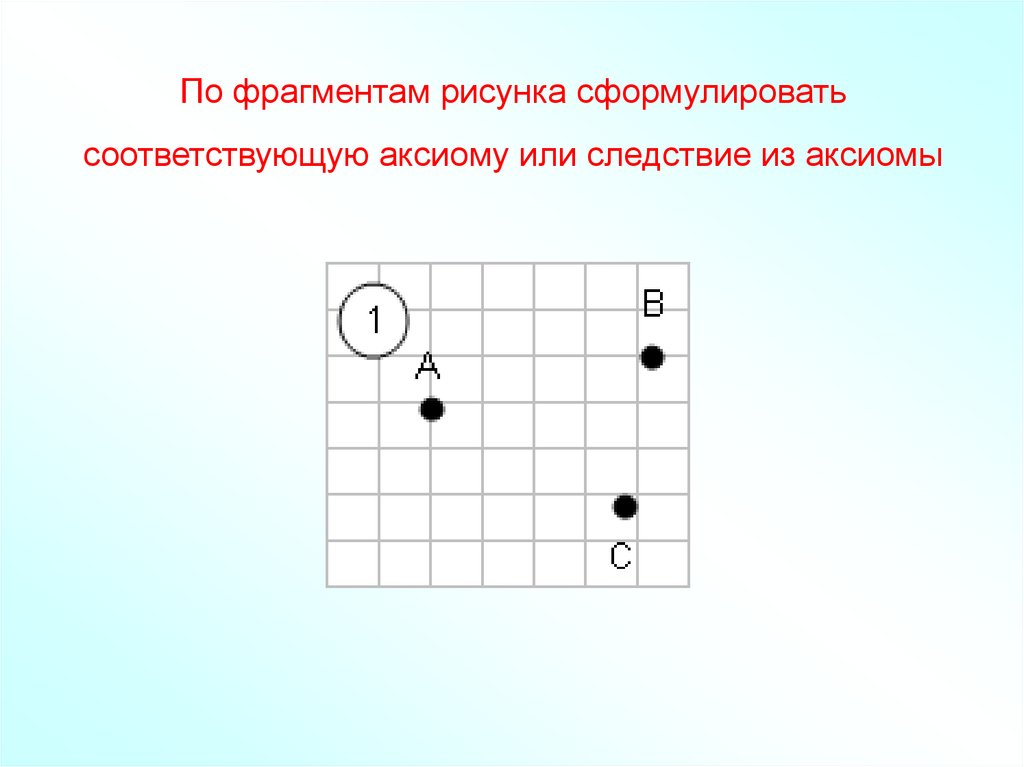
По фрагментам рисунка сформулироватьсоответствующую аксиому или следствие из аксиомы
39. По фрагментам рисунка сформулировать соответствующую аксиому или следствие из аксиомы
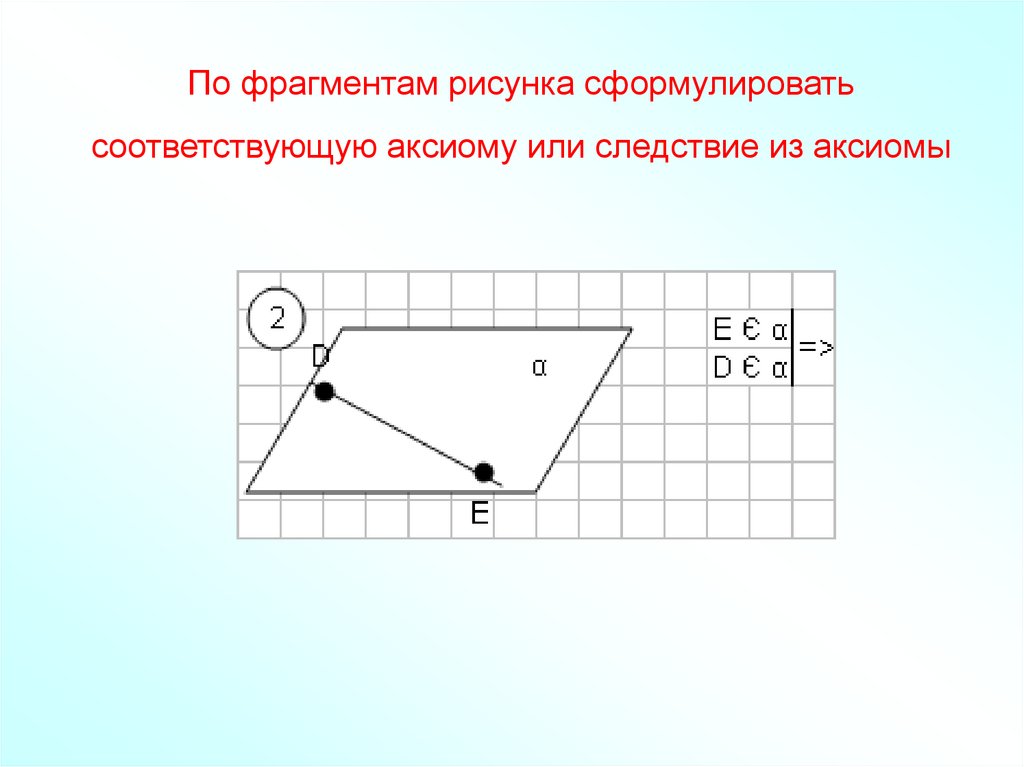
40. По фрагментам рисунка сформулировать соответствующую аксиому или следствие из аксиомы
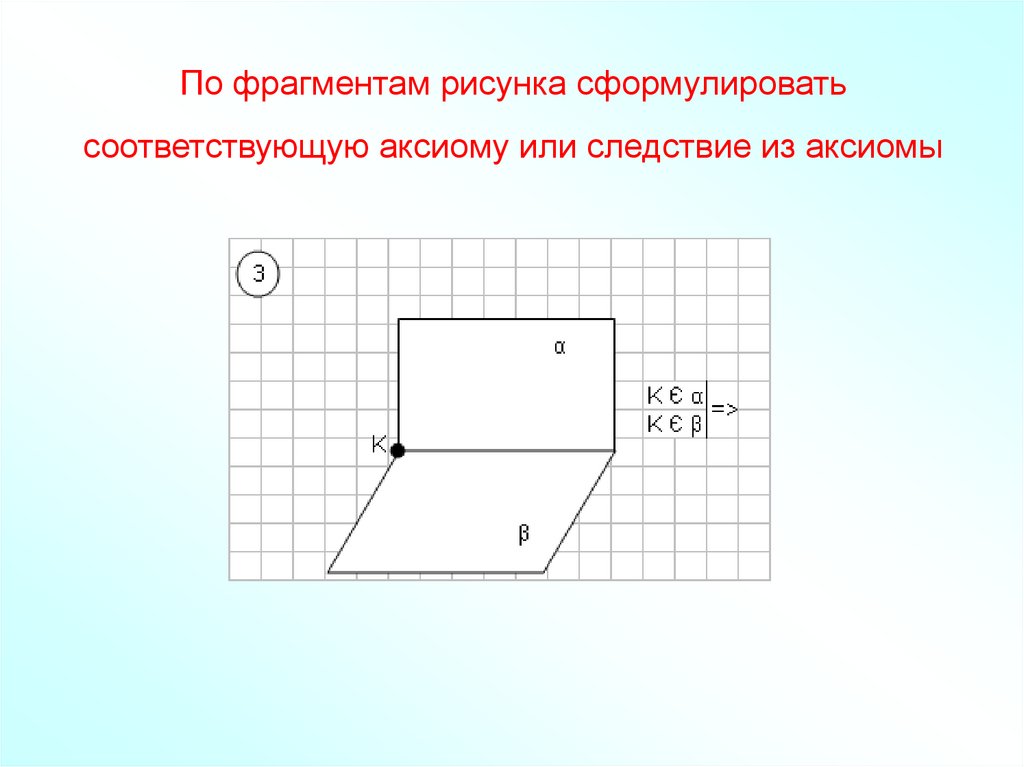
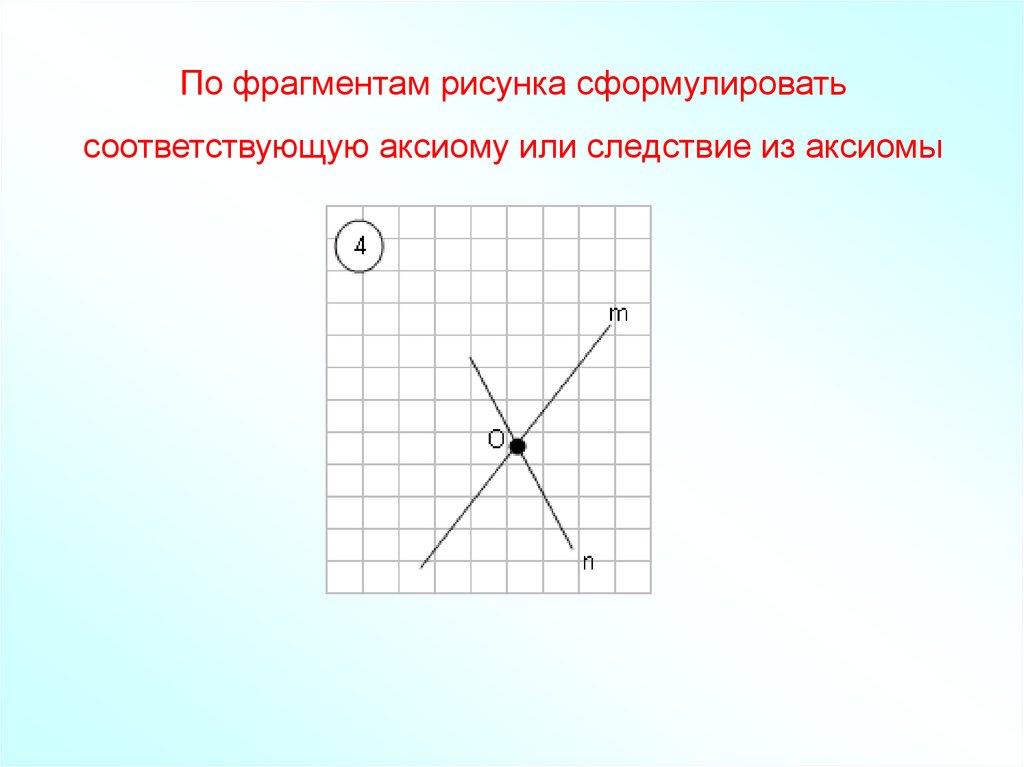
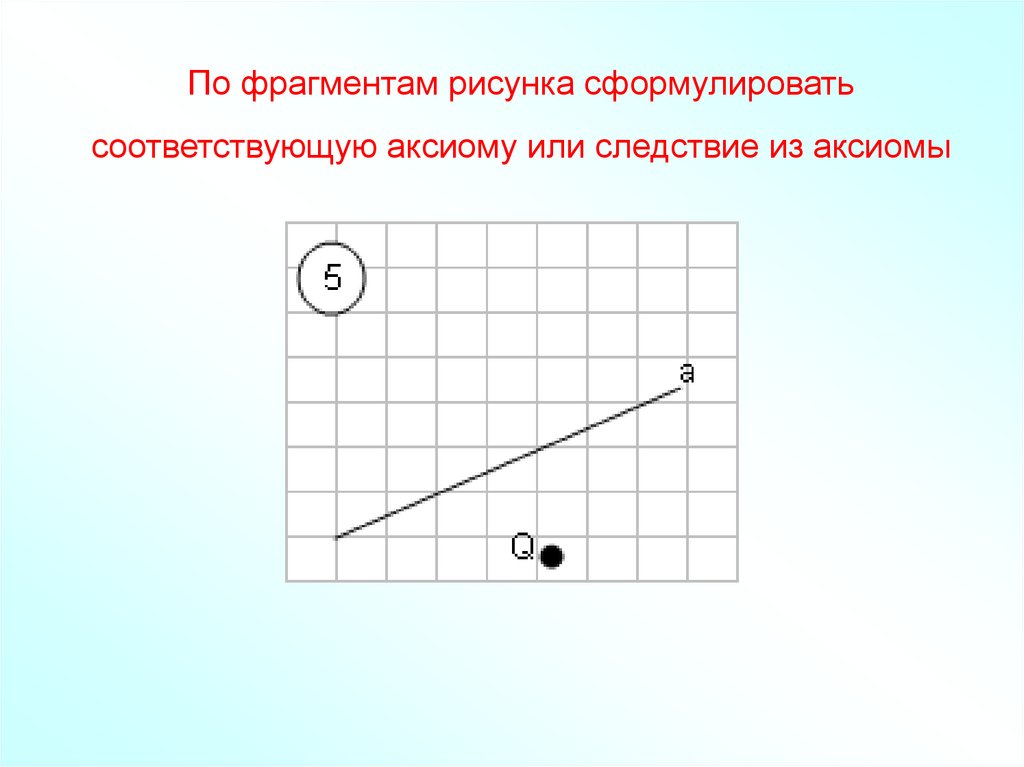
41. По фрагментам рисунка сформулировать соответствующую аксиому или следствие из аксиомы
42. По фрагментам рисунка сформулировать соответствующую аксиому или следствие из аксиомы
43. По фрагментам рисунка сформулировать соответствующую аксиому или следствие из аксиомы
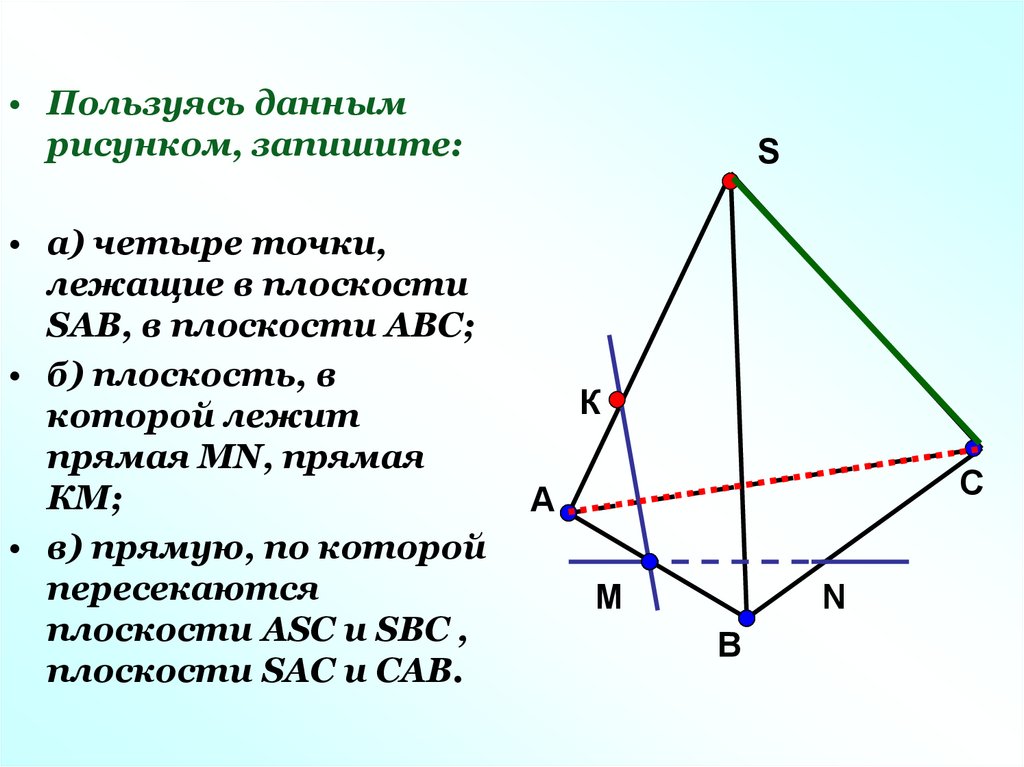
• Пользуясь даннымрисунком, запишите:
• а) четыре точки,
лежащие в плоскости
SAB, в плоскости АВС;
• б) плоскость, в
которой лежит
прямая MN, прямая
КМ;
• в) прямую, по которой
пересекаются
плоскости ASC и SBC ,
плоскости SAC и CAB.
S
К
C
А
М
N
В
44.
D1А1
С1
В1
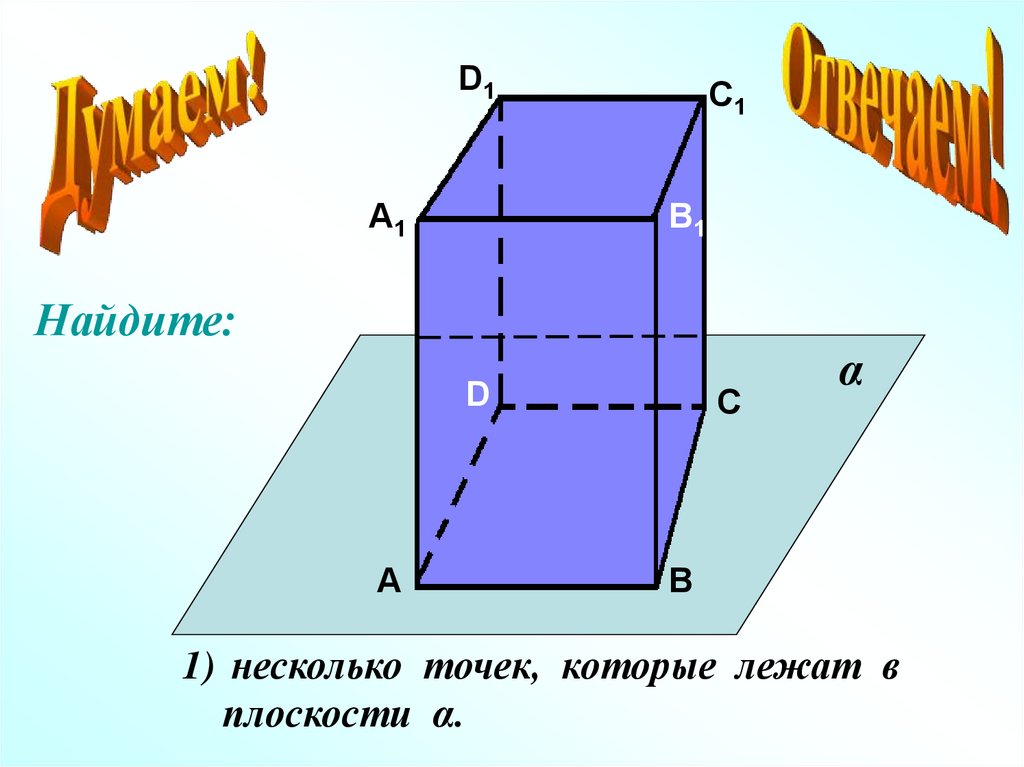
Найдите:
D
А
С
α
В
1) несколько точек, которые лежат в
плоскости α.
45.
D1А1
С1
В1
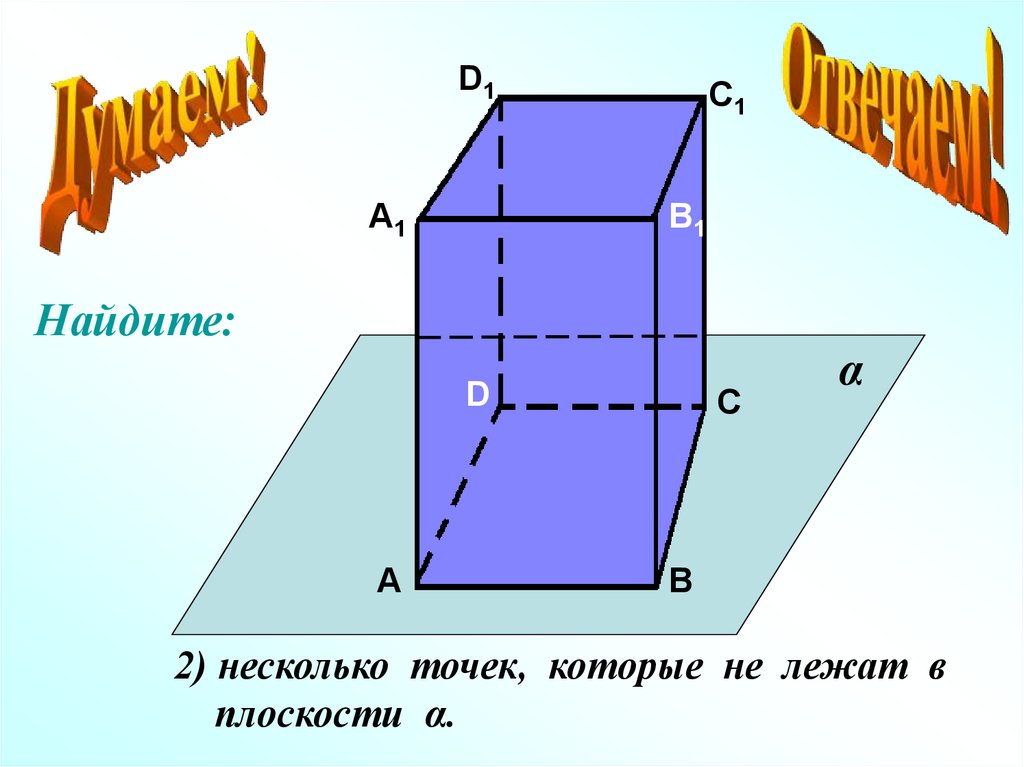
Найдите:
D
А
С
α
В
2) несколько точек, которые не лежат в
плоскости α.
46.
D1А1
С1
В1
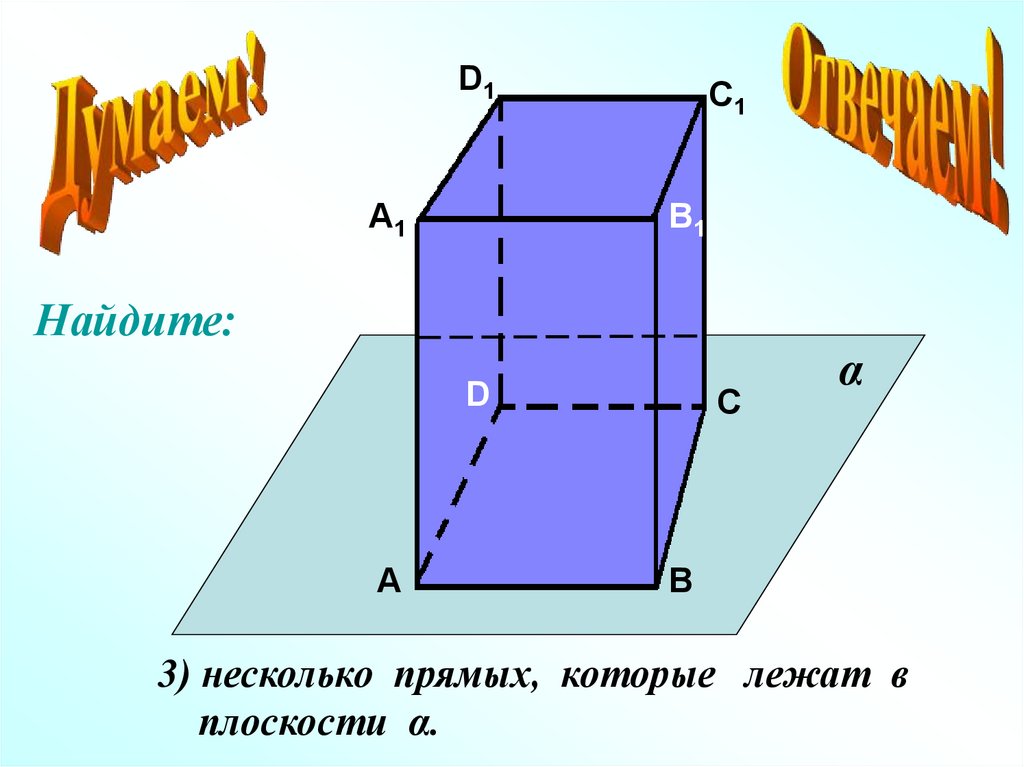
Найдите:
D
А
С
α
В
3) несколько прямых, которые лежат в
плоскости α.
47.
D1А1
С1
В1
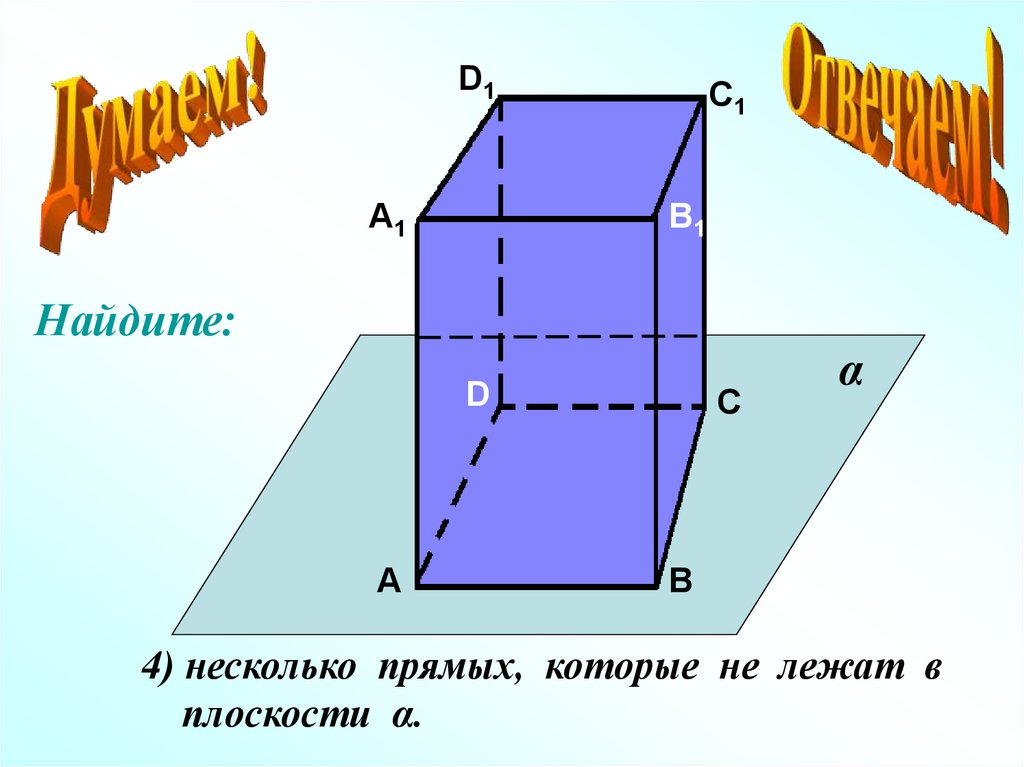
Найдите:
D
А
С
α
В
4) несколько прямых, которые не лежат в
плоскости α.
48.
D1А1
С1
В1
Найдите:
D
А
С
α
В
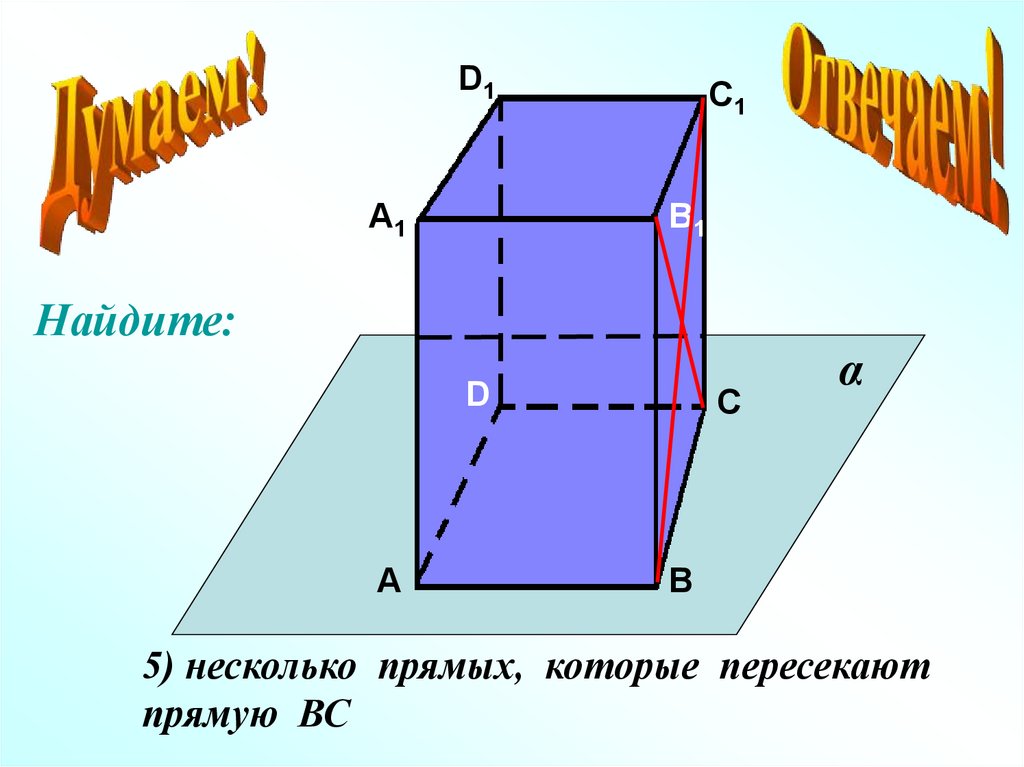
5) несколько прямых, которые пересекают
прямую ВС
49.
D1А1
С1
В1
Найдите:
D
А
С
α
В
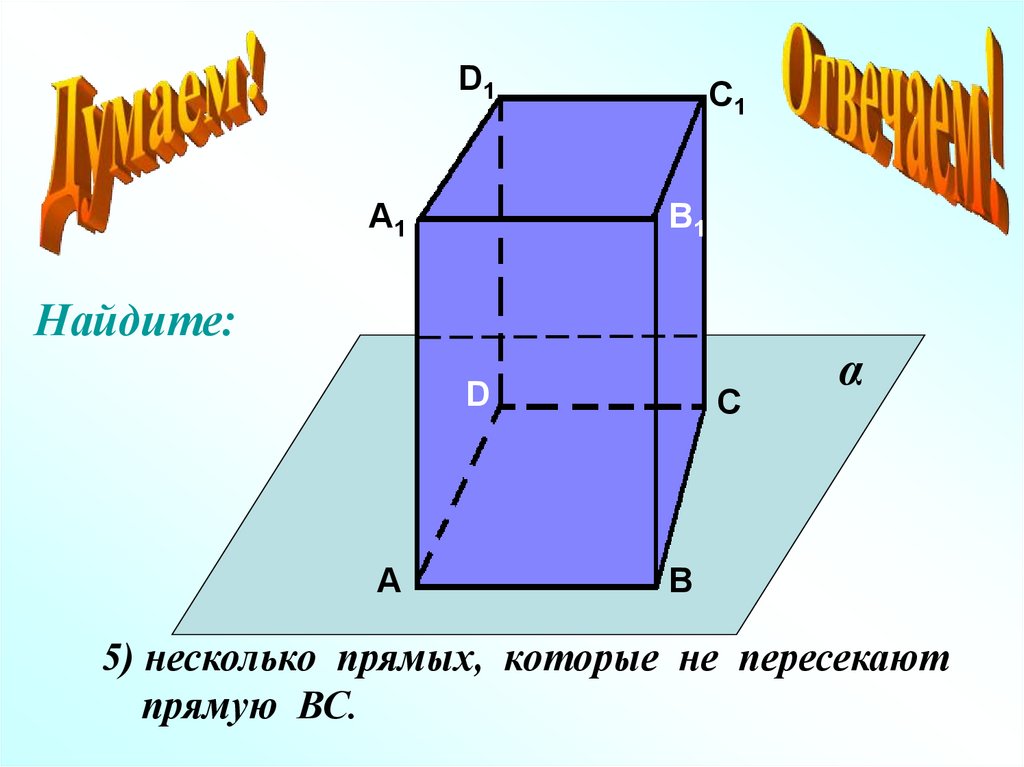
5) несколько прямых, которые не пересекают
прямую ВС.
50.
Дан куб АВСDA1B1C1D1.D1
С1
M
А1
В1
N
D
С
K
А
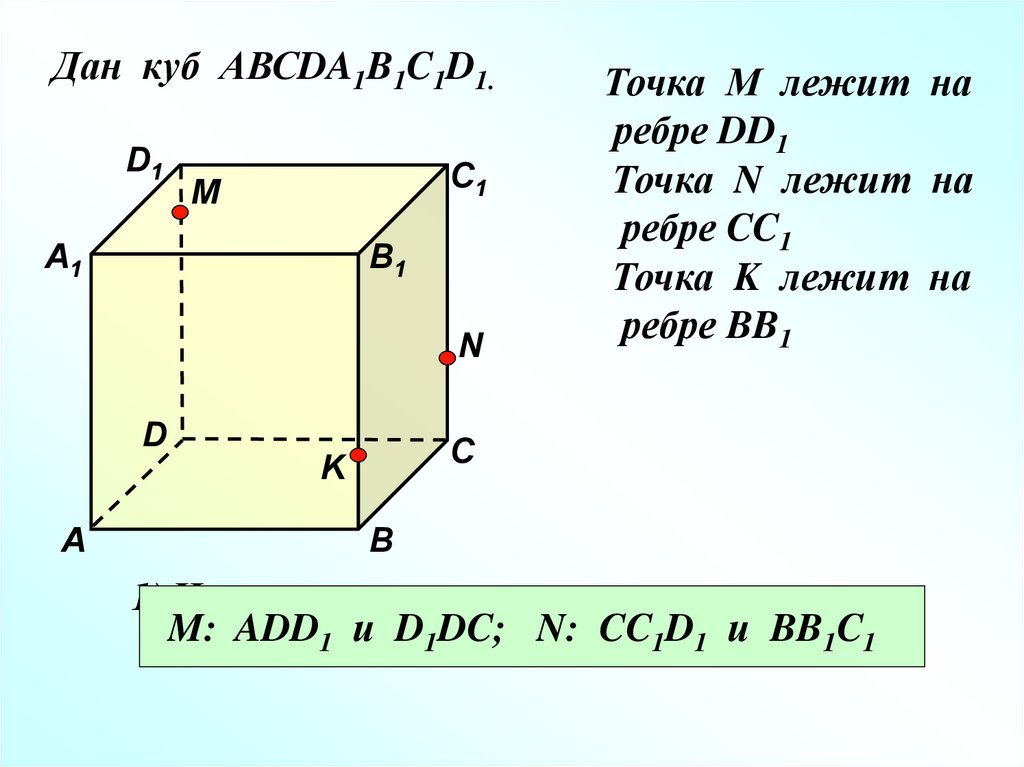
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
В
1) Назовите плоскости в которых лежат
M:
ADDМ,
D1DC;N.N: CC1D1 и BB1C1
1 иточка
точка
51.
Дан куб АВСDA1B1C1D1.D1
С1
M
А1
В1
N
F
D
С
K
А
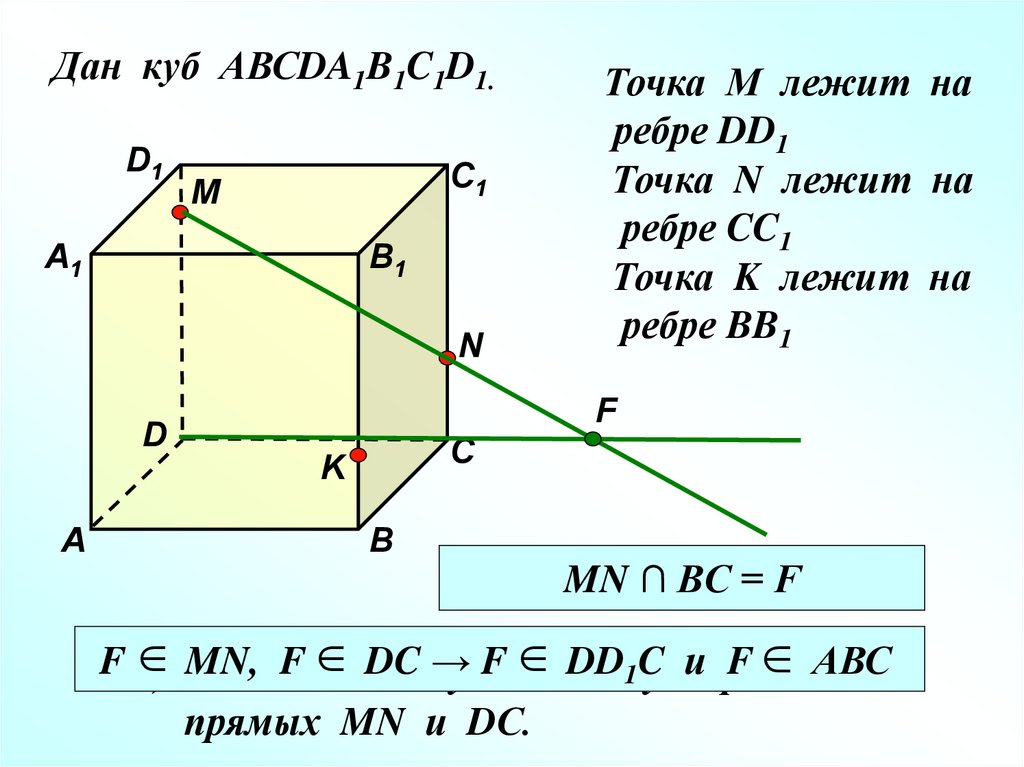
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
В
MN ∩ BC = F
Каким
свойством
обладает
F 2) Найдите
MN, F точку
DC → FF
DD1C
– точку
прямых MN и DС.
точка
F?
и F АВС
пересечения
52.
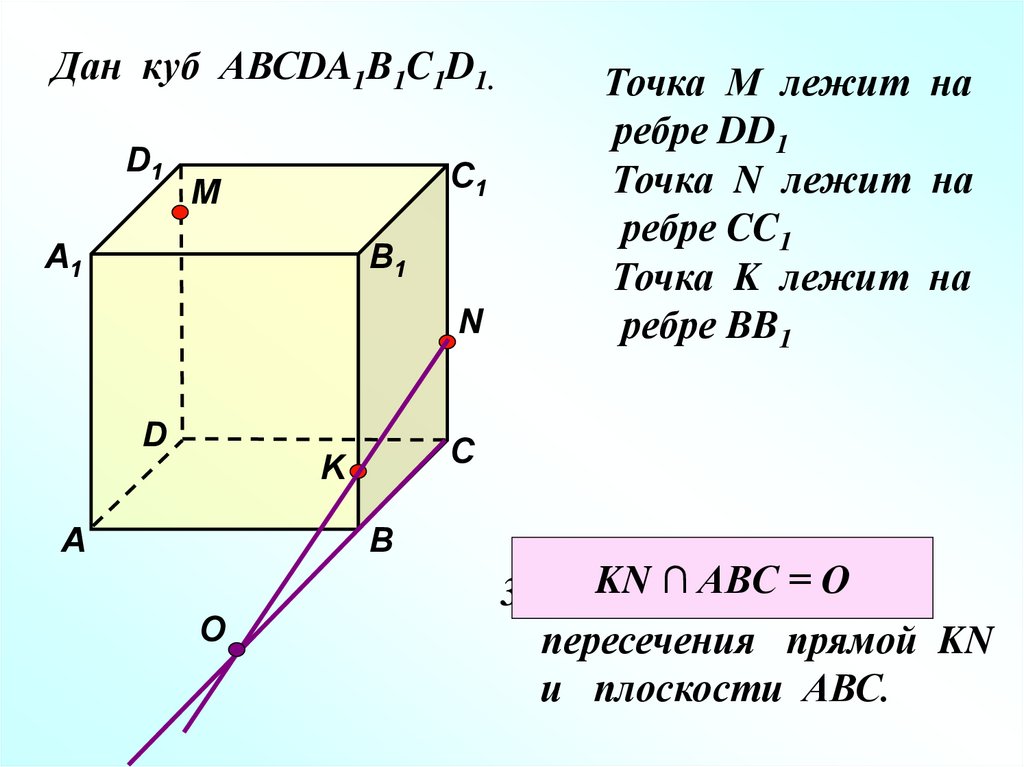
Дан куб АВСDA1B1C1D1.D1
С1
M
А1
В1
N
D
С
K
А
В
О
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
KN ∩ ABC
=O
3) Найдите
точку
пересечения прямой KN
и плоскости АВС.
53.
54.
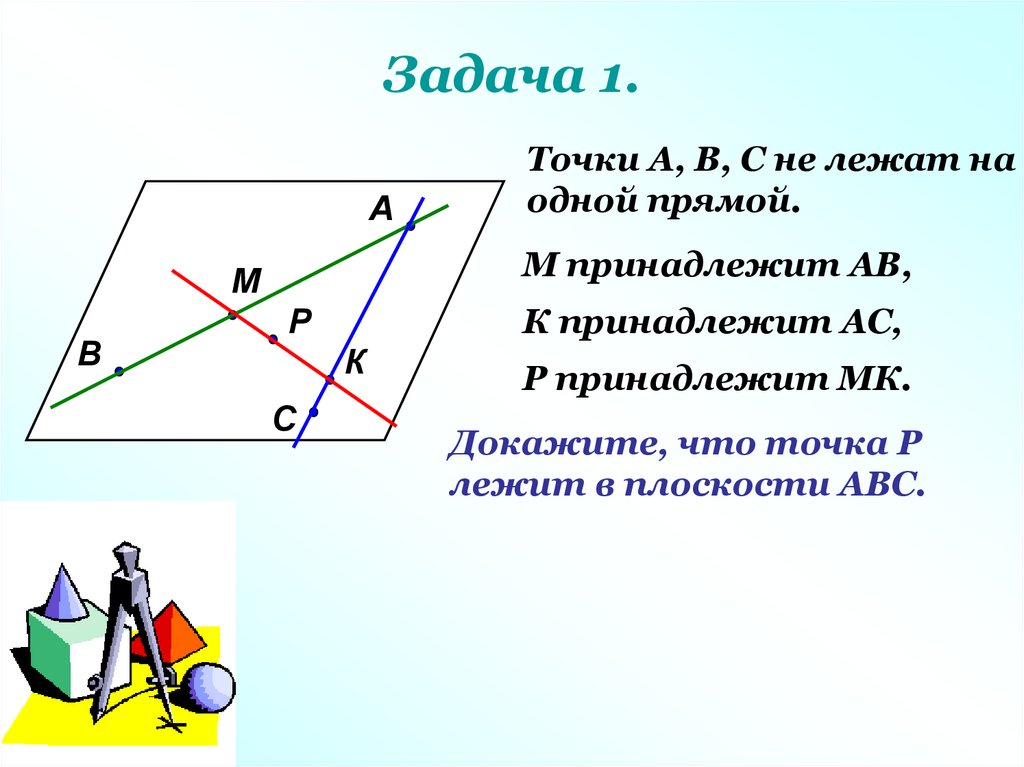
Задача 1.А
М принадлежит АВ,
М
В
Точки А, В, С не лежат на
одной прямой.
К принадлежит АС,
Р
К
С
Р принадлежит МК.
Докажите, что точка Р
лежит в плоскости АВС.
55. Задача 1.
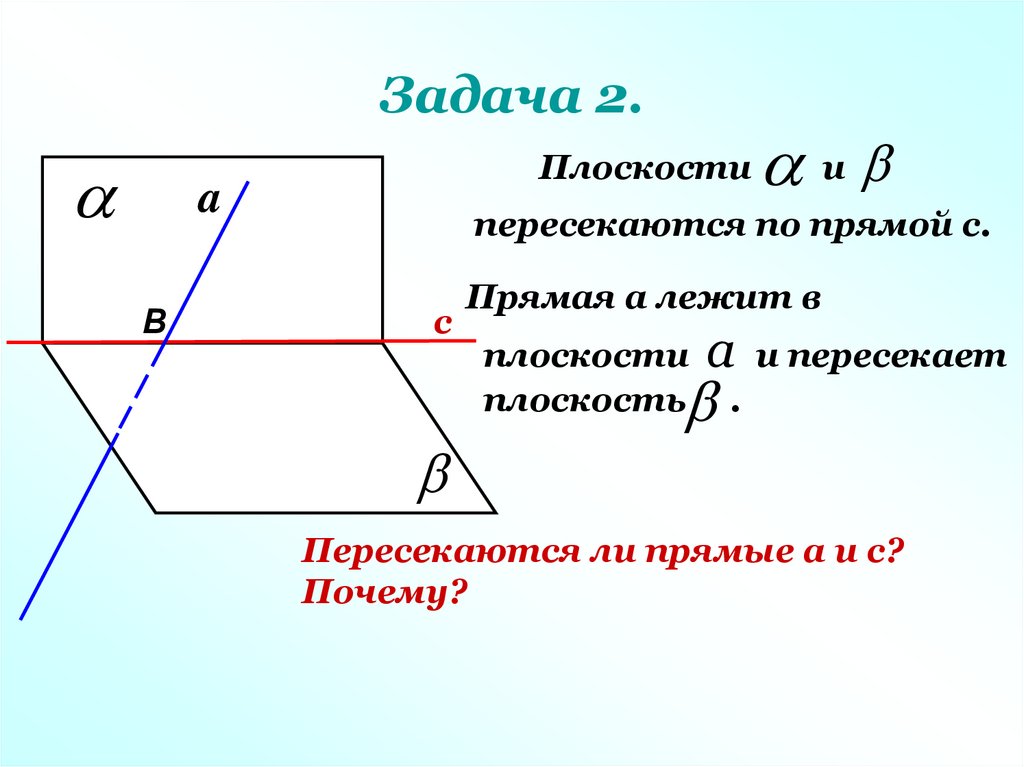
Задача 2.Плоскости
a
В
и
пересекаются по прямой с.
с
Прямая а лежит в
плоскости
плоскость
а
.
и пересекает
Пересекаются ли прямые а и с?
Почему?
56. Задача 2.
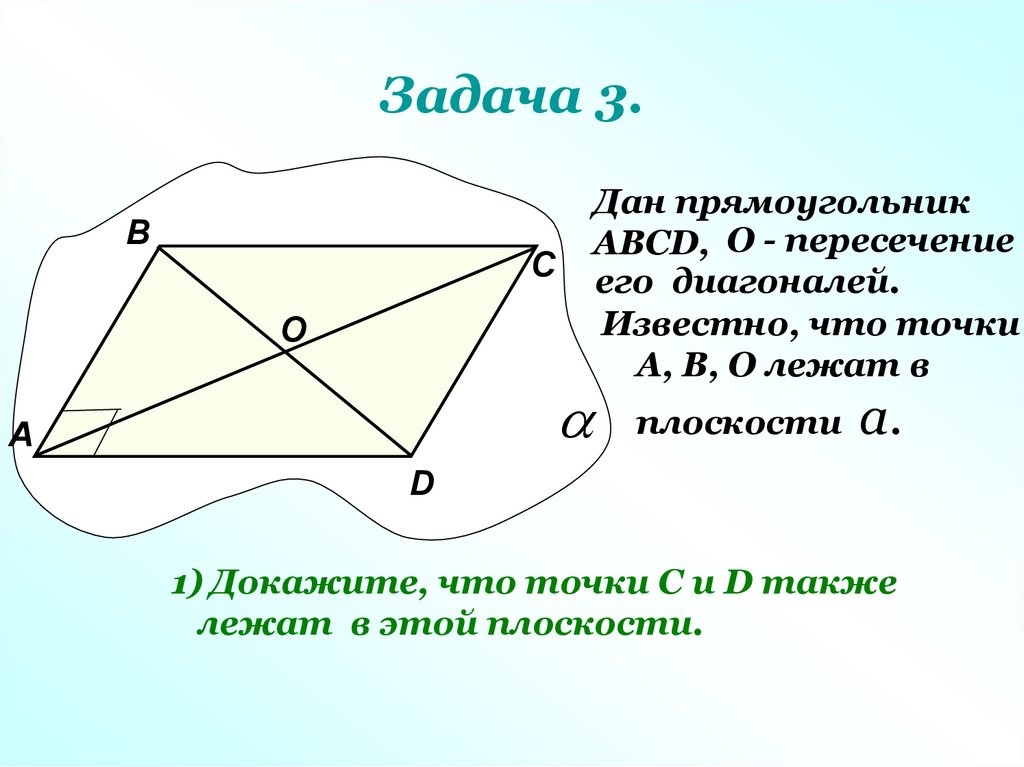
Задача 3.В
С
О
А
Дан прямоугольник
АВСD, О - пересечение
его диагоналей.
Известно, что точки
А, В, О лежат в
плоскости
а.
D
1) Докажите, что точки С и D также
лежат в этой плоскости.
57. Задача 3.
1) Ответить на вопросы диктанта,приведенного ниже (1 вариант)
2) Решить задачи, приведенные ниже.
58.
Диктант.№1
Необходимо ответить на вопросы:
1 вариант.
2 вариант
1. Назовите основные фигуры
на плоскости.
2. Сформулируйте аксиому А2
1. Назовите основные фигуры
в пространстве.
2. Сформулируйте аксиому А1
3. Могут ли прямая и
плоскость иметь две общие
точки?
3. Сколько плоскостей можно
провести через прямую и не
лежащую на ней точку?
4. Сколько плоскостей можно
провести через три точки?
4. Сформулируйте аксиому А3
5. Сколько может быть
общих точек у прямой и
плоскости?
5. Могут ли прямая и
плоскость иметь одну общую
точку?
59. Диктант.
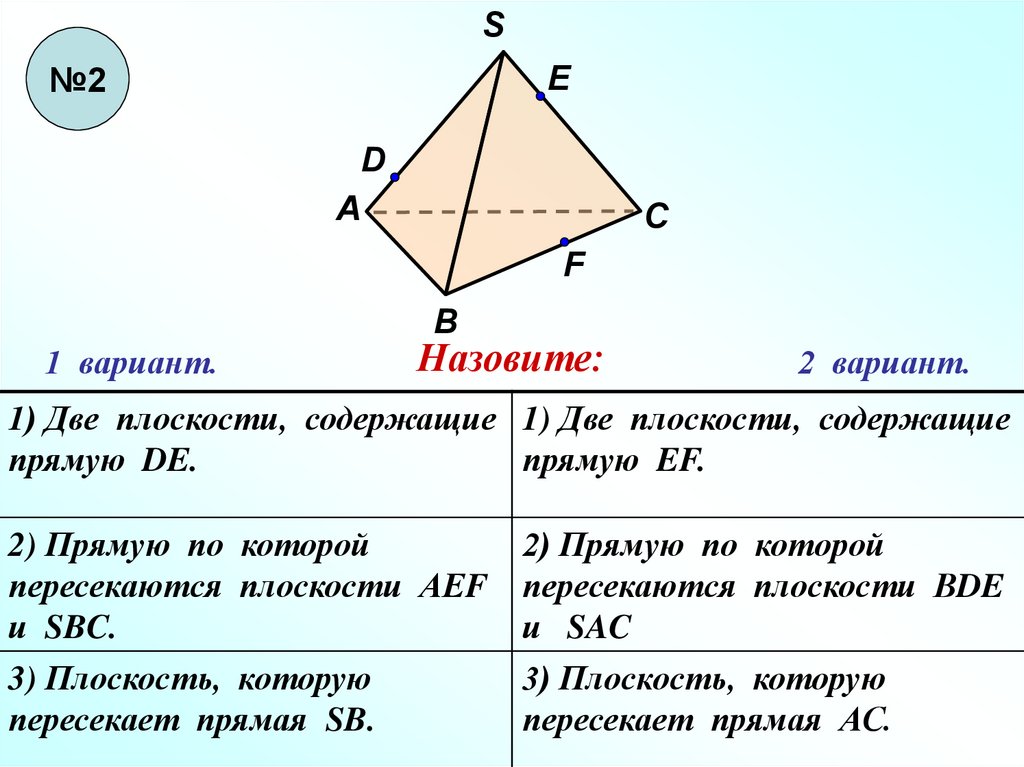
S№2
E
D
А
С
F
В
1 вариант.
Назовите:
2 вариант.
1) Две плоскости, содержащие 1) Две плоскости, содержащие
прямую DE.
прямую EF.
2) Прямую по которой
2) Прямую по которой
пересекаются плоскости АЕF пересекаются плоскости ВDE
и SBC.
и SAC
3) Плоскость, которую
3) Плоскость, которую
пересекает прямая SB.
пересекает прямая АС.
60.
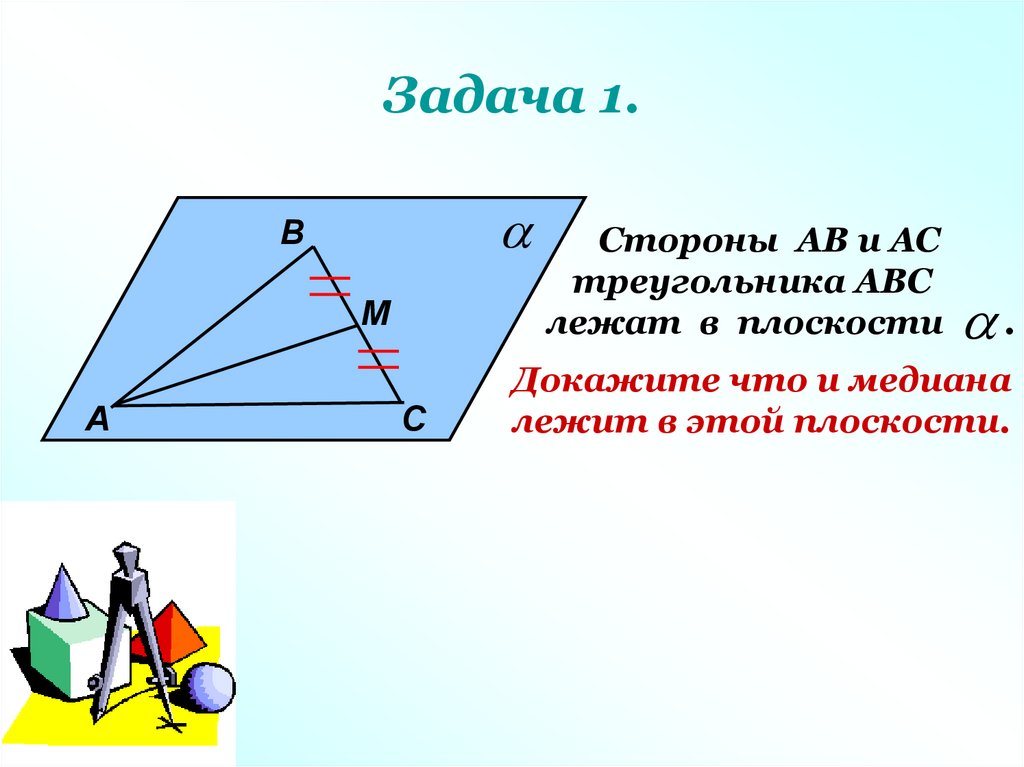
Задача 1.В
М
А
С
Стороны АВ и АС
треугольника АВС
лежат в плоскости
.
Докажите что и медиана
лежит в этой плоскости.
61. Задача 1.
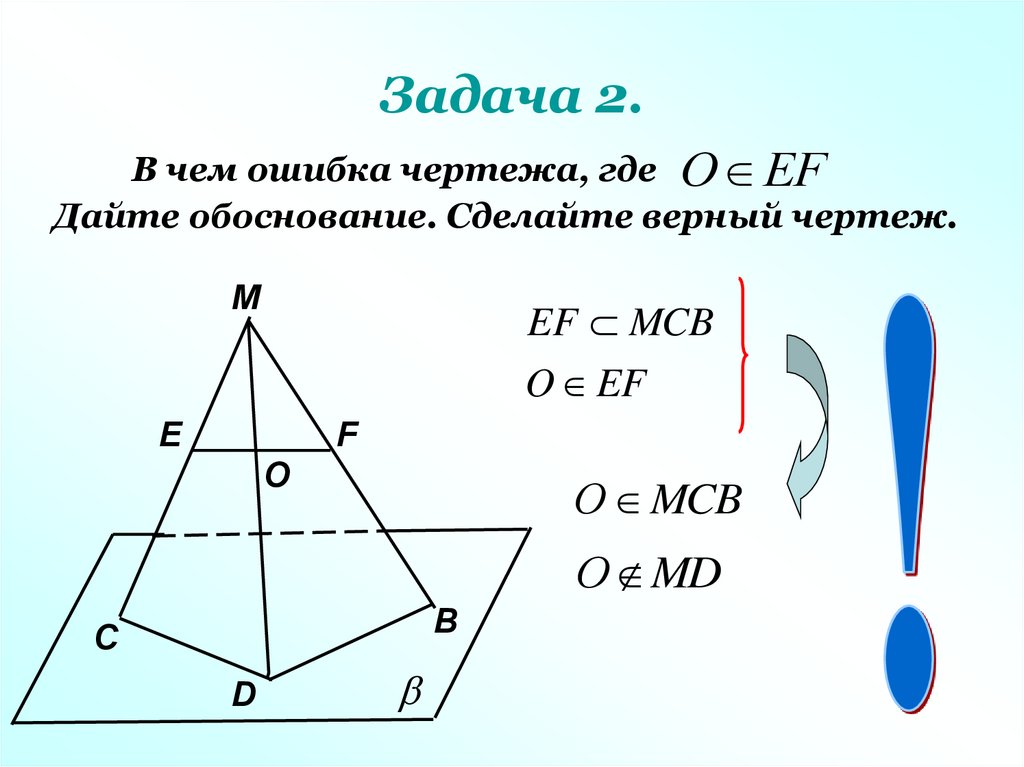
Задача 2.В чем ошибка чертежа, где О ЕF
Дайте обоснование. Сделайте верный чертеж.
M
EF MCB
O EF
E
F
O
О MCB
О MD
В
С
D


















 mathematics
mathematics








