Similar presentations:
Процессы изменения состояния термодинамических систем
1.
Процессы изменения состояниятермодинамических систем
Классификация термодинамических процессов
Термодинамический процесс может быть задан
либо графическим способом в виде изображения
процесса в координатах p-v, p-T, Т-s, либо в аналитической форме в виде зависимости ( p ,v ) 0
Уравнение процесса может быть также задано
исходным условием о неизменном значении в этом
процессе какой - либо функции состояния
z idem; z p ,v ,t ,u ,h,s
или условием о равенстве нулю какого – либо эффекта
термодинамического процесса
q 0
2.
При изучении термодинамических процессовопределяются:
1) закономерность изменения параметров состояния
рабочего тела, то есть выводится уравнение процесса
или дается его графическое изображение в
координатах p-v, p-T, Т-s и т.д.;
2) параметры состояния системы в начальной и конечной
точках процесса;
3) численные значения работы и теплообмена в
процессе;
4) изменение значений внутренней энергии, энтальпии и
энтропии рабочего тела.
Простейшие термодинамические процессы
Простейшими термодинамическими процессами
обычно считают изобарный, изохорный и
изопотенциальные процессы.
3. Изобарный процесс – процесс в котором давление в системе остается постоянным
Изобарный процесс p idem ;dp 0
– процесс в
котором давление в системе остается постоянным
.
P
P1
P= idem
1
2
1,2
v1
v2 v
4.
Изобарные процессы подвода или отвода теплотыпроисходят в поршневых двигателях внутреннего
сгорания, газотурбинных, паросиловых, холодильных
установках и др.
Для идеального газа в изобарном процессе (1-2)
соотношение объемов прямо пропорционально
соотношению температур
T2 v2
T1 v1
Удельная термодинамическая и потенциальная
работы в изобарном процессе определяются из
соотношений
2
w1,2 v dp 0; l1,2 p dv p v2 v1
2
1
1
5.
Для идеального газаl1,2 p v2 v1 R T2 T1
Количество теплоты, подведенной к рабочему телу
или отведенной от него в изобарном процессе, определяется из выражения первого начала термодинамики
q1, 2 u l1, 2 h
Для идеального газа
q1, 2 u l1, 2 h
cvm (T2 T1 ) R T2 T1 c pm T2 T1
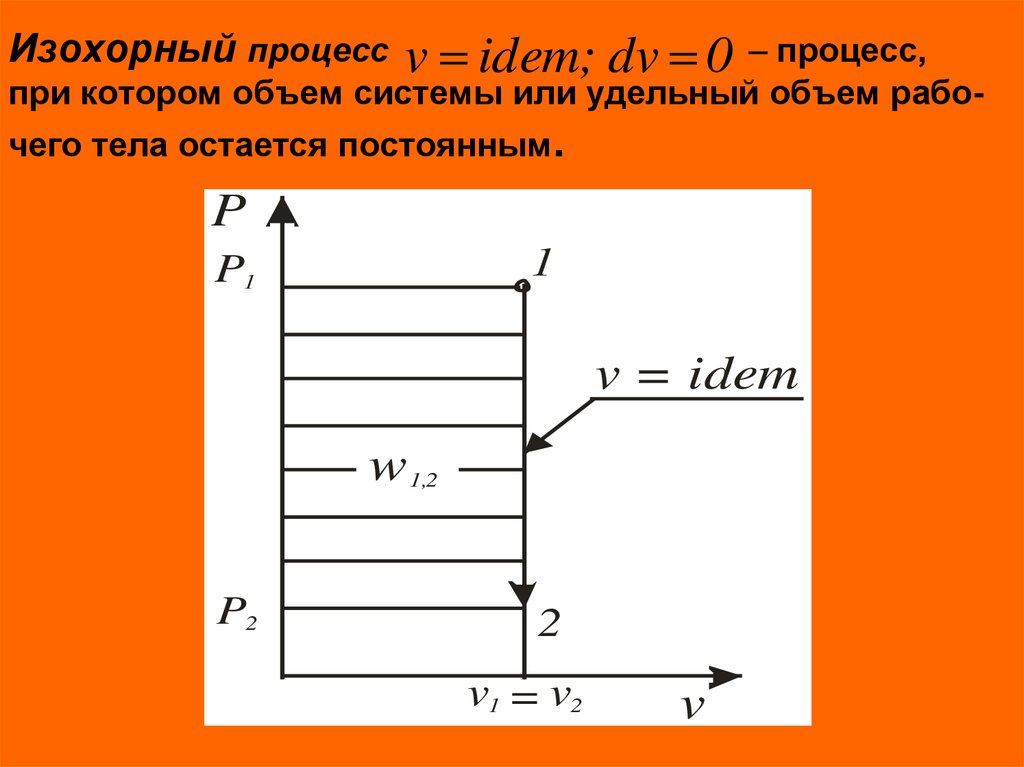
6. Изохорный процесс – процесс, при котором объем системы или удельный объем рабо- чего тела остается постоянным.
Изохорный процессv idem; dv 0 – процесс,
при котором объем системы или удельный объем рабочего тела остается постоянным.
P
1
P1
v = idem
w 1,2
P2
2
v1 = v2
v
7.
В изохорных процессах происходит увеличениеили уменьшение давления, что связано с соответствен –
ным изменением температуры – подводом или отводом
теплоты.
Изохорные процессы подвода или отвода теплоты
происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых установках и др.
Для идеального газа в изохорном процессе
соотношение давлений прямо пропорционально
соотношению температур
T2
p2
T1
p1
8.
Удельная термодинамическая и потенциальнаяработы в изохорном процессе определяются из соотношений
l1,2 p dv 0; w1,2 1 vdp v p1 p2
2
2
1
Для идеального газа
w1,2 v p1 p2 R T1 T2
Количество теплоты, подведенной к рабочему телу
или отведенной от него в изохорном процессе, определяется из выражения первого начала термодинамики
9.
q1, 2 h w1, 2 uДля идеального газа
q1, 2 h w1, 2 u
c pm T2 T1 R T1 T2 cvm T2 T1
Изопотенциальный процесс – термодинамический
процесс изменения состояния системы, при котором
значение потенциальной функции сохраняет неизменное
значение pv idem; d ( pv ) 0
10.
Для идеального газа, согласно уравнению Клапейронаpv RT изопотенциальный процесс pv idem
является и изотермическим T idem .
p2 v2 T2
p1v1 T1
Удельная термодинамическая и потенциальная работы
в изопотенциальном процессе определяются из следующих соотношений:
2
2
v2
dv
l1,2 p dv p v pv ln
v1
v
1
1
1
2
2
p1
dp
dp
pv ln
w1,2 v dp vp pv
p2
p
2 p
1
1
11.
Нетрудно заметить, что постоянствоприводит к условию
pv idem
p1 v2
p2 v1
Поэтому, в изопотенциальном процессе численные
значения термодинамической и потенциальной работ
равны между собой.
p1
v2
l1,2 w1,2 pv ln pv ln
p2
v1
12.
Для идеального газа pv=RT=idem (изотермический)l1,2
p1
v2
w1,2 RT ln RT ln
p2
v1
Количество теплоты, подведенной к рабочему телу
или отведенной от него в изопотенциальном процессе
определяется из выражения первого начала
термодинамики по балансу рабочего тела
q1, 2 u l1, 2 h w1, 2
Для идеалного газа du=0; dh=0
v2
p1
q1,2 RT ln RT ln
v1
p2
13. Адиабатный процесс - термодинамический процесс изменения состояния системы, при котором отсутствует теплообмен и в силу
Адиабатный процесс - термодинамический процессизменения состояния системы, при котором отсутствует
теплообмен q 0 и в силу обратимости процесса
энтропия остается величиной постоянной s idem
14.
Из выражения первого начала термодинамики дляпростого тела при условии q 0 имеем s idem
q q q du pdv dh vdp 0
*
**
Отсюда следует выражение для показателя
адиабатного процесса
dh
vdp
ns k
du
pdv
где ns=k – показатель адиабаты.
Расчетное выражение для расчета показателя
адиабатного процесса
15.
dpp d ln p d log p
ns k
.
dv
d ln v
d log v
v
После интегрирования при условия постоянства
показателя процесса имеем
h w1,2
ns k
u l1,2
p1
log
p2
v2
log
v1
Для идеального газа показатель адиабаты равен
k= cp/cv
16.
Из уравнения адиабатного процесса получимвыражение для связи параметров состояния
v2
p1
k log
log
,
v1
p2
потенцируя имеем
k
1
k
p2 v2 v2 p2
1
p 1 v1
v1 p 1
pv idem;
k
1
pkv
idem;
17.
Выражения конечных (интегральных) величинтермодинамической и потенциальных работа в адиабатном процесс можно получить при сопоставлении их
элементарных значений
l pdv,..... w vdp
l w pdv vdp d pv
С учетом определения показателя адиабаты имеем:
l w 1 k l d pv
1
l
d pv
1 k
18.
Интегрируя последнее выражение с учетом того,что k=idem, получим интегрального уравнения
термодинамической работы
2
1
1
l1,2
d ( pv )
( p1v1 p2v2 ) u1 u2
1 k
1 1 k
Введем понятие характеристики процесса
расширения или сжатия
1,2
p2 v2
p1v1
19.
Окончательно имеем уравнения для определениятермодинамической и потенциальной работы
l1,2
p1v1
1 1,2 u1 u2
k 1
k
w1,2 kl1,2
p1v1 1 1,2 h1 h2
k 1
Различные уравнения для определения характеристики расширения или сжатия 1,2 определяются с
учетом уравнения адиабаты
k 1
k 1
p2v2 p2 k v1
1,2
p1v1 p1
v2
20.
Применительно для идеального газа имеем:l1, 2
RT1
1 1,2 cvm t1 t2
k 1
k
w1, 2 kl1, 2
R1T1 1 1, 2 c pm t1 t2
k 1
k 1
k
T2 p2v2 p2
T1 p1v1 p1
v1
v2
k 1
1,2
21.
Уравнения перечисленных простейших и любыхдругих термодинамических процессов могут быть
представлены одним уравнением. Это уравнение называется уравнением политропы, а термодинамические
процессы, описываемые этим уравнением, называются
политропными.
Политропные процессы
Политропным процессом с постоянным показателем
называется обратимый термодинамический процесс
изменения состояния простого тела, подчиняющийся
уравнению
pv idem C ;
n
p
n
p1v1
1/ n
v idem C1 ;
n
p 2 v2
22.
где п – показатель политропы, являющий врассматриваемом процессе постоянной величиной,
которая может иметь любые частные значения положительные и отрицательные (- n + ).
Физический смысл показателя политропы п
определяется после дифференцирования уравнения
политропы pv n idem C ;
v dp n v
n
n 1
pdv 0
vdp w w1,2
n
pdv l l1,2
23.
24.
Это значит, что постоянный показательполитропы определяется соотношением потенциальной
и термодинамической работ в элементарном или
конечном процессах. Значения этих работ могут быть
определены графически в координатах p v
В логарифмических координатах политропный
процесс (политропа) с постоянным показателем
представляет собой прямую линию
log p n log v log C
При этом, постоянный показатель политропы
определяется как тангенс угла наклона линии процесса к
оси абсцисс ( )
25.
log( p1 / p2 )w vdp d log p
n
tg
log( v2 / v1 )
l
pdv d log v
Из соотношения показателя политропи следует, что
для изобарного процесса n p 0 , для изохорного процесса
nv = ± ∞, для изопотенциальног процесса npv = 1 (для
идеального газа n pv nt nu nh =1 , это означает, что для
идеального газа изоротенциальный, изотермический,
изоэнергетический и изоэнтальпийный процессы совпа
дают), для адиабатного процесс n = k.
26.
Работа в политропных процессахВыражения конечных (интегральных) величин
термодинамической и потенциальных работ в политропных процессах
l1,2
n
p1v1
p1v1 1 1,2
1 1,2 ; w1,2 n l1,2
n 1
n 1
1,2
n 1
n
p 2 v 2 p2
v1
p1v1 p1 v2
для идеального газа pv = RT и
1,2
n 1
p2v2 T2
p1v1 T1
27.
Теплообмен в политропном процессе для простыхтел выводится также на основе рассмотрения
выражения первого начала термодинамики
q du l .
Удельная внутренняя энергия для простых тел может
быть представлена в виде функции u =и (p, v).
Тогда дифференциал внутренней энергии запишется в
следующем виде:
u
u
du dv dp
dv p
dp v
Последнее выражение можно представить в виде
1 u
1 u
du pdv vdp
p dv p
v dp v
28.
Введем следующие обозначения:1 u
av ,
p dv p
1 u
a p
v dp v
При этом выражение примет вид:
du av l a p w
av l a p n l ( av n a p ) l
Подставив полученное уравнение в выражение первого
начала термодинамики
q du l .
получим
29.
q ( av n a p 1 ) l .Для определения величин ( a p и a v ) рассмотрим два
термодинамических процесса:
Изоэнергетический процесс (u = idem, du = 0 ,n = nu.)
Так как в изоэнергетическом процессе
av nu a p 0 ,
l 0 ,
av nu a p
Адиабатный процесс ( q = 0). Для этого процесса
показатель политропы принимает значение n = k и элементарная термодинамическая работа также не равна нулю
av k a p 1 0 , nu a p ka p 1 отсюда
1
ap
,
k nu
nu
av
k nu
30.
С учетом полученных соотношений для определения av иap, находим выражения для расчета удельных значений
изменения внутренней энергии и теплообмена в элементарном
процессе:
nu n
du
l ,
k nu
k n
q
l
k nu
Соотношения для расчета удельных значений изменения
внутренней энергии и теплообмена в конечном процессе имеют
следующий вид:
u1,2
nu n
l1,2 ;
k nu
Для идеального газа nu = 1
q1,2
k n
l1,2
k nu































 physics
physics








