Similar presentations:
Техническая термодинамика (1 часть)
1. Техническая термодинамика (1 часть)
1.32.
Уравнение Майера• Энтальпия i u pv
• Продифференцируем di du d pv
• Разделим на dТ
di du d pv du RdT
dT dT
dT
dT
dT
di du
R
dT dT
R c p cv ;
Дж
кг К
• Для 1 кмоля
c p cv R 8,314;
кДж
кмоль К
3. Энтропия
• Теплота не является функцией состояния(зависит от пути процесса)
• Умножаем теплоту на интегрирующий
множитель
1
T
• И назовем q
T
ds
ее приведенной теплотой
q du pdv cv dT Rdv
ds
T
T
T
T
v
p R
T v
4.
q• Приведенная теплота T при обратимом
изменении состояния газа полный
дифференциал некоторой функции
переменных Т и v
• Клаузиус назвал эту функцию энтропией и
обозначил s;
Дж/(кг К) или Дж/К
• Таким образом
q
ds
T
5. Дж/К
• Энтропия – функция состояниятермодинамической системы, определяемая
тем, что ее дифференциал dS при
элементарном равновесном (обратимом)
процессе, происходящем в этой системе, равен
отношению бесконечно малого количества
теплоты Q, сообщенного системе, к
термодинамической температуре системы
Q
dS
T
Дж/К
6. II закон термодинамики
• I закон утверждает, что можетQ L
и
L Q
не устанавливая условий, при которых
возможны эти превращения
• I закон не рассматривает вопрос о
направлении теплового процесса, а не зная
направления нельзя предсказать характер и
результат
7.
• Закон, позволяющий указать направлениетеплового потока и устанавливающий
максимально возможный предел превращения
Q L в тепловых машинах, представляет
собой II закон термодинамики
• Постулат Клаузиуса: Теплота не может
переходить от холодного тела к более
нагретому сама собой даровым процессом (без
компенсации)
• Томсон: Не вся теплота, полученная от
теплоотдатчика, может перейти в работу, а
только некоторая ее часть, а другая часть
теплоты должна перейти в теплоприемник
8. Математическое выражение II закона термодинамики
qds
T
• Оценка степени необратимости
(несовершенства)
• Анализ процессов
9. Изменение энтропии для любого термодинамического процесса
q du pdv cv dT Rdvds
T
T
T
T
v
T2
v2
s cv ln R ln
T1
v1
q di vdp c p dT Rdp
ds
T T
T
T
p
T2
p2
s c p ln R ln
T1
p1
10. Термодинамические процессы идеальных газов
• К основным процессам, имеющим большоезначение как для теоретических
исследований, так и для практических работ,
относят
• - изохорный (v-const),
• - изобарный (p-const),
• - изотермический (T-const),
• - адиабатный (q=0).
11.
• Кроме того существует группа процессов,являющихся при определенных условиях
обобщающими для основных.
• Эти процессы называются политропными и
характеризуются постоянством
теплоемкости в процессе.
12.
• Для всех процессов устанавливается общийметод исследований:
• 1) выводится уравнение кривой
• 2) устанавливается взаимосвязь между p, v, T в
начале и конце процесса
• 3) определяется изменение внутренней энергии
u
• 4) вычисляется работа изменения объема l
• 5) располагаемая (полезная) работа l
• 6) изменение энтальпии i
• 7) количество теплоты q
• 8) изменение энтропии s
13. Изохорный процесс
p1 p2p
1) const
2)
T1 T2
T
3) u cv (T2 T1 )
4) dl pdv 0
5) dl vdp
l 0
l v( p2 p1 )
6) dq di vdp
7) dq du pdv du
8)
T2
s cv ln
T1
p
p1
1
p2
2
= const
1 = 2
i q v( p2 p1 ) q l
q u cv (T2 T1 )
14. Изобарный процесс
v1 v2v
1) const
2)
T1 T2
T
u q l
3)
4) dl pdv
l p(v2 v1 )
5)
dl vdp 0
6)
i c p (T2 T1 )
8)
p = const
p1 = p2
1
2
1
2
l 0
7) dq di vdp di
T2
s c p ln
T1
p
q i c p (T2 T1 )
15. Изотермный процесс
1) pv const3) du cv dT
2) p1v1 p2v2
u 0
p
p1
1
T = const
p = const
2
p2
1
2
v2
p1
l RT ln p1v1 ln
v1
p2
p1
v2
l RT ln
p1v1 ln
p2
v1
v2
p1
di
c
dT
i
0
8)
6)
s R ln R ln
p
v1
p2
dq du pdv pdv dl
7)
q l l
dq di vdp vdp dl
RT
4) dl pdv
dv
v
RT
dp
5) dl vdp
p
16.
Адиабатный процессp
1
p1
1) Из уравнений 1 закона термодинамики получим
du pdv 0
сv dT pdv 0
di vdp 0
Разделим второе на первое уравнение
с p dT
vdp
сv dT
pdv
так как
q=0
2
p2
1
2
с p dT vdp 0
сp
сv
k
то
l
k
l
l kl
17.
vdpk
pdv
v2
p2
dv
dp
k
v
p
v1
p1
dv
dp
k
v
p
проинтегрируем
v2
p2
p1
k ln ln
ln
v1
p1
p2
После потенцирования имеем
k
v2
p1
p2
v1
pv p v
k
1 1
k
2 2
Откуда получаем уравнение адиабатного процесса (адиабаты)
pv const
k
где k – показатель адиабаты
Газы
k
Одноатомные
1,67
Двухатомные
1,4
Трех- и многоатомные
1,29
18.
2)p2 v1
p1 v2
3)
du dl
4)
k
T2 v1
T1 v2
k 1
T2 p2
T1 p1
u l
dl pdv
R
l
T1 T2
k 1
k 1
v1
p1v1
l
1
k 1 v2
1
l
p1v1 p2v2
k 1
k 1
k
RT1 p2
l
1
k 1 p1
k 1
k
19.
l kl5) dl vdp
k
l
p1v1 p2v2
k 1
k
l
R T1 T2
k 1
k 1
k
p2
k
l
RT1 1
p1
k 1
k 1
v1
k
l
p1v1 1
k 1
v2
6) di vdp dl
7)
dq 0
q 0
i l
dq
0
8) ds
T
s 0
s const
Адиабатный процесс называют изоэнтропным
20.
Политропный процессНаряду с изобарным, изохорным, изотермическим и адиабатным
процессами можно представить еще бесконечное множество процессов,
у которых имеются другие постоянные признаки.
Всякий процесс идеального газа, в котором теплоемкость является
постоянной величиной, называется политропным.
Из определения следует, что если основные термодинамические
процессы (изобарный, изохорный, изотермический и адиабатный)
протекают при постоянной теплоемкости, то они являются частными
случаями политропного.
Для политропного процесса количество теплоты
q cn (T2 T1 )
dq cn dT
21.
dq cn dT du pdvdq cn dT di vdp
cn dT сv dT pdv
c
dT
с
dT
vdp
n
p
Перенесем слагаемые с теплоемкостями в правую сторону,
вынесем dT за скобки,
разделим второе уравнение на первое
cn с p
vdp
cn сv
pdv
обозначим
vdp l
n
pdv l
n
cn с p
cn сv
22.
vdpn
pdv
v2
p2
dv
dp
n
v
p
v1
p1
dv
dp
n
v
p
проинтегрируем
v2
p2
p1
n ln ln
ln
v1
p1
p2
После потенцирования имеем
n
v2
p1
p2
v1
pv p v
n
1 1
n
2 2
Откуда получаем уравнение политропного процесса (политропы)
pv n const
где n – показатель политропы
23.
Из уравненийn
cn с p
сp
cn сv
сv
k
Найдем теплоемкость политропного процесса
n k
cn сv
n 1
Показатель политропы и теплоемкость для процессов
Для основных процессов
процесс
Изохорный
Изобарный
Изотермический
Адиабатный
показатель политропы
теплоемкость
n=
n=0
cп = сv
cп = kсv= сp
n=1
n=k
cп =
cп = 0
24.
2)p2 v1
p1 v2
n
n 1
T2 p2
T2 v1
T1 p1
T1 v2
3) u c (T T ) n 1 q n 1 l
v
2
1
n k
1 k
1
l
p1v1 p2v2
4) dl pdv
n 1
R
l
T1 T2
k 1
n 1
k
RT1 p2
l
1
k 1
n 1 p1
p1v1 v1
l
1
n 1 v2
n 1
n
25.
5) dl vdpl nl
n
l
p1v1 p2v2
n 1
n
l
R T1 T2
n 1
6)
i c p (T2 T1 )
c
dT
dq
n
8) ds
T
T
k 1
k
p2
n
l
RT1 1
p1
n 1
k 1
v1
n
l
p1v1 1
n 1
v2
7) q cn (T2 T1 )
T2
n k T2
s cп ln cv
ln
T1
n 1 T1
26.
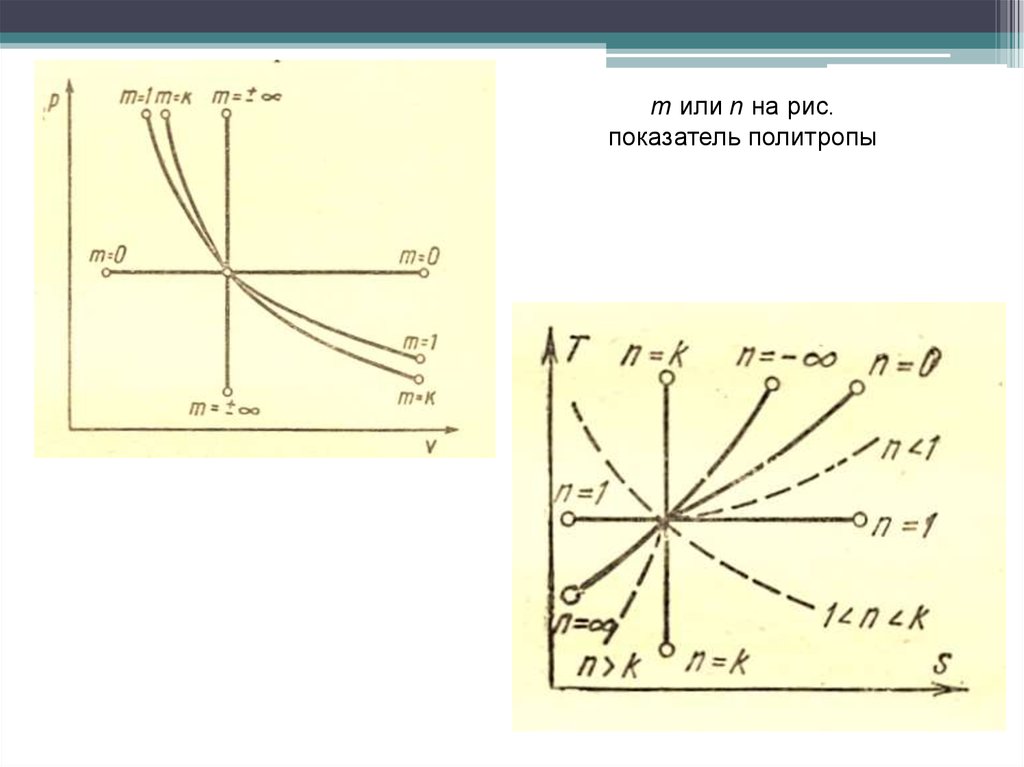
m или n на рис.показатель политропы

























 physics
physics








