Similar presentations:
Техническая термодинамика
1. Основная литература
1.2.
3.
4.
5.
Теплотехника: учеб. для технич. специальностей
вузов / В. Н. Луканин и др.; под ред. В.Н.
Луканина. – М.: Высш. шк., 2009. – 671 с.
Нащокин, В.В. Техническая термодинамика и
теплопередача : учеб. пособие для неэнергет.
специальностей вузов / В.В. Нащокин. – М.: Азбук, 2008. – 469 с.
Алабовский, А.Н. Техническая термодинамика и
теплопередача / А.Н. Алабовский, И.А.
Недужий. – Киев: Высшая школа, 1990. – 225 с.
Техническая термодинамика / под ред. В.П.
Крутова. – М.: Высшая школа, 1991. – 384 с.
СТП 3.4.204-01 Требования к оформлению
текстовых документов. / Ермолина Т.В. –
Красноярск: - СибГТУ, 2011. - 46 с.
2. Что такое термодинамика?
Термодинамика изучает законы превращенияэнергии в различных процессах, происходящих в
макроскопических системах и сопровождающихся
тепловыми эффектами
Техническая термодинамика изучает
закономерности взаимного преобразования
тепловой и механической энергии.
3. Что такое теплотехника?
Теплотехника – наука о способах получения,транспортировки и использования тепловой
энергии в виде горячей воды, водяного пара и
газовой теплоты.
4.
Тепловая энергия – это энергия хаотическогодвижения молекул и атомов газа.
Механическая энергия – это энергия
движения макроскопических тел (человека,
автомобиля, самолета).
5.
Преобразование тепловой энергии вмеханическую можно
осуществить только в тепловом двигателе:
● двигателе внутреннего сгорания (ДВС),
● паротурбинной установке (ПТУ),
● газотурбинной установке (ГТУ).
Преобразование тепловой энергии в
механическую в тепловом двигателе происходит
при расширении газообразного рабочего тела
6. Параметры состояния рабочего тела
Основные параметры состояния:Абсолютное давление;
Удельный объем;
Абсолютная температура.
7.
Давление газа (Н/м2) - сумма импульсовмолекул, приходящихся на единицу
поверхности в единицу времени.
1 Атмосферное давление (В, Рб)
В=f(Н,t)
2 Избыточное давление (Ри)
3 Абсолютное давление (Ра)
Ра=Ри+В
4 Вакууметрическое давление (W)
Ра=В-W
8.
Объем – пространство, занимаемое телом, м3Удельный объем – это объем 1 кг газа, м3/кг:
v=V/m,
где
V – полный объем газа, м3;
m – масса газа, кг.
Величина, обратная удельному объему, называется
плотностью – массой 1 м3 газа, кг/м3:
ρ=m/V.
Отсюда следует, что их произведение равно единице:
ρv=1.
9.
Температура характеризует нагретость тела ипредставляет собой меру средней кинетической
энергии тела.
T=B(mc2/2)
где В - постоянная Больцмана;
с – скорость.
Т,К=t, С+273,15.
За 0 С принята температура плавления льда
при атмосферном давлении , а за 100 С –
температура кипения воды.
10.
Идеальный газ – это газ, состоящий изнедеформируемых молекул, не имеющих
собственного объема и не
взаимодействующих между собой.
О2, N2, Н2, воздух - идеальные газы.
11.
Состояния идеальных газов описываются законами:1 Закон Гей-Люссака: Р=Const
v2/v1=T2/T1
или
v/Т=Const;
При постоянном давлении объемы одинаковых масс одного и
того же газа относятся как абсолютные температуры.
2 Закон Бойля-Мариотта:T=Const
p2 /p1=v1/v2
или
pv=Const;
Произведение давления на объем определенной массы одного и
того же газа для различных его состояний, но при одинаковой
температуре есть величина постоянная.
3 закон Шарля:v=Const
p2/p1=T2/T1
или
p/T=Const.
Давление газа фиксированной массы и объема прямо
пропорционально абсолютной температуре газа.
12.
Уравнение состояния идеального газа1 Для 1 кмоль газа
pVμ = RμT
Rμ = 8314 Дж/(кмоль К) – универсальная газовая постоянная, одинаковая
для всех газов
Физический смысл Rμ – это работа совершаемая 1 кмоль вещества при
нагревании на 10С в процессе при постоянном давлении.
2 Для 1 кг газа
РV=RT
R = Rμ/ μ = 8314/μ кДж/(кг*К) – удельная газовая постоянная, зависящая от
химической структуры газа
3 Для произвольной массы газа m:
РV=mRT
13. Смеси идеальных газов
Газовая смесь – это вещество состоящее изразличных компонентов не вступающих в
реакцию между собой.
Закон Дальтона:
p = p1 + p2 + ' ' ' + pn = Σpi
Парциальное давление pi - давление, которое
имел бы компонент, если бы он один
занимал весь объем смеси
Pi pVi / V
где Vi – приведенный объем компонента
14. Способы задания смеси
1 Весовые (массовые) долиgi = mi / М
R=ΣRi *qi
2 Объемные (мольные) доли
ri = Vi / V
1
R n
ri
i 1 Ri
3 Мольная доля компонента равна объемной доле: mi=ri
15. Молекулярная масса смеси
Молекулярная масса смеси равна сумме произведениймолекулярных масс компонентов на их мольные (объемные) доли
n
см ( i ri )
см
1
n
qi
i 1
где
i
qi
ri
i 1
i
- молекулярная масса отдельных компонентов смеси;
- весовая доля компонентов смеси;
- объемная доля компонентов смеси.
Парциальное давление отдельного компонента
Ri
pi g i
p
Rсм
Vi
pi p ri p
V
16. Соотношение между массовыми и объемными долями компонентов
Riri qi
Rсм
17. Теплоемкости газов
Теплоемкость – это количество тепла, необходимое длянагрева тела на один градус.
Удельная теплоемкость – количество тепла, необходимое
для нагревания единицы количества вещества на один
градус.
В зависимости от единиц измерения количества вещества
различают :
- массовую теплоемкость – С , Дж / (кг К);
- объемную теплоемкость – С’, Дж / (м3 К);
- мольную теплоемкость - Сµ , Дж / (кмоль К).
18.
Между различными видами теплоемкостей существует следующаязависимость:
C=Cμ/μ; C’=Cμ/22,4; C’=C ·ρ
Различают истинную (С) и среднюю (Сm)теплоемкость:
Истинная теплоемкость - теплоемкость рабочего тела,
соответствующая бесконечно малому изменению его температуры
С = dq / dT.
Средняя теплоемкость рабочего тела - теплоемкость
соответствующая конечному изменению его температуры
рабочего тела:
Сm = q1-2 / (t2 – t1).
Количество теплоты, необходимое на нагрев тела, можно
определить следующим образом:
Q = m Сm (t2 - t1).
19.
Теплоемкость зависит от способа подводатеплоты к газу.
Чаще всего используют 2 способа:
Изобарная теплоемкость (Cp) при P=const
CP =dqp/dT
Изохорная теплоемкость(Cv) при V=const
Cv =dqv/dT
20. Уравнение Майера
Теплоемкости при постоянном давлении и постоянномобъеме связаны между собой следующими соотношениями:
ср– сv= R
Коэффициента Пуассона (показателя адиабаты)
сp /сv=k
Когда не требуется большой точности, принимают следующие значения k:
1 атомные газы k=1,67
2-х атомные газы k=1,40
3-х атомные газы k=1,33
21.
Массовую Ссм и объемную С’см теплоёмостьгазовых смесей определяют по формулам:
Cсм = Σ (Ci gi ); C’см= Σ (C’i ri ) ,
где
Ci – массовая теплоемкость отдельного газа, Дж / (кг К);
gi – массовые доли газов, составляющих смесь;
C’i – объемная теплоемкость отдельного газа, Дж / (м3 К);
ri – объемные доли газов, составляющих смесь.
22. Термины и общие понятия
Термодинамическая система (т.д. система)– совокупностьматериальных тел, взаимодействующих как между собой, так
и с окружающей средой. По своей роли тела, входящие в
систему делятся на рабочие тела и источники или
потребители энергии.
Окружающая среда – совокупность тел, не входящих в
термодинамическую систему.
Т.д. системы бывают: открытые, закрытые, изолированные и
адиабатные
23. Термины и общие понятия
Термодинамический процесс – изменениесостояния термодинамической системы
вследствие воздействия на нее внешней
среды.
24. Термины и общие понятия
Если параметры состояния одинаковы во всехточках системы, то состояние называется
равновесным.
Процесс, состоящий из последовательности
равновесных состояний, называется
равновесным.
Процесс, в результате совершения которого в
прямом и обратном направлениях, система
возвращается в начальное состояние без
изменений в окружающей среде, называется
обратимым. Равновесные процессы обратимы.
25. I закон термодинамики
Является частным случаем закона сохранения энергии.Теплота и работа эквивалентны Q = L
Теплота, сообщаемая системе, идет на приращение
внутренней энергии и на совершение работы.
Q = ΔU + L - для массы газа G кг
q = Δu + l – для 1 кг газа
где
Q [Дж] – теплота затраченная на нагрев рабочего тела массой m (кг);
q [Дж/кг] – теплота затраченная на нагрев рабочего тела массой 1 кг;
L [Дж] – работа совершенная рабочим телом количеством m (кг);
l [Дж/кг] – работа совершенная рабочим телом количеством 1 кг;
∆U [Дж] – изменение внутренней энергии рабочего тела массой m (кг);
Δu [Дж/кг] – изменение внутренней энергии рабочего тела массой 1 кг.
26. Внутренняя энергия (U)
Внутренняя энергия – энергия хаотического движениямолекул и атомов, внутримолекулярная и потенциальная
энергия сил взаимодействия между молекулами.
u E
пост
кин
E
вращ
кин
E
колеб
кин
3
Eпот Eкин Eпот
1
Но в тепловых процессах изменяется только кинетическая и
потенциальная энергии. Остальные остаются постоянными.
Для идеального газа
27. Внутренняя энергия (U)
Внутренняя энергия идеального газа, в котором отсутствуют силывзаимодействия между молекулами, не зависит от объема газа
или давления, а определяется только его температурой.
Внутренняя энергия как тепловая характеристика состояния это
есть количество теплоты необходимое для нагревания рабочего
тела в процессе при постоянном объеме.
Сvm – средняя теплоемкость рабочего тела при постоянном
объеме, Дж / (кг К).
28. Работа газа (L) и рабочая диаграмма P-V
dS1 кг
p
1(p1, v1)
2(p2,v2)
4
0
3
dv
v
Пусть в цилиндре находится
1 кг газа при давлении p>pатм.
Газ стремится расшириться и
перемещает поршень, то есть
совершает положительную
работу +l, Дж/кг.
При сжатии над газом
совершается отрицательная
работа -l.
dl=pfdS=pdv,
где p – давление, Па;
v - удельный объем газа, м3/кг;
f – сечение поршня, м2;
dS – перемещение поршня, м.
29. Теплота (Q)
Любое тело обладает внутренней энергией, но нетеплотой.
При соприкосновении двух тел они обмениваются
внутренней энергией в форме теплоты q, Дж/кг
(процесс теплообмена между телами).
Теплота – это форма проявления внутренней
энергии в том или ином термодинамическом
процессе.
Теплота, подведенная к газу – положительная;
отведенная от газа – отрицательная.
30. I закон термодинамики
Теплота, сообщаемая системе, идет наприращение внутренней энергии и на
совершение работы.
Q = ∆U + L
Вечный двигатель первого рода —
неограниченно долго действующее
устройство, способное бесконечно
совершать работу без затрат топлива
или других энергетических ресурсов.
31. Энтальпия и энтропия
Энтальпия – это теплота, подводимая к телу в процессе нагрева его припостоянном давлении. Единицы измерения полной энтальпии (Н) джоуль, удельной энтальпии (h) – джоуль на килограмм.
Энтропия – функция состояния термодинамической системы, которая
характеризует хаотичность (неупорядоченность) системы. Единицы
измерения полной энтропии (S) – джоуль на кельвин, удельной энтропии (s)
– джоуль на килограмм-кельвин .
32. Термодинамические процессы идеальных газов
Изохорный – процесс при неизменном объеме газа:v=Const.
Изобарный – при постоянном давлении газа:
p=Const.
Изотермический – при постоянной температуре газа:
T=Const.
Адиабатный – без теплообмена между газом и окружающей
средой:
q=0 или S=Const.
Политропный – процесс без ограничений.
33. Исследование термодинамических процессов
1) Построить процесс в PV- и TS- диаграммах.2) Определить начальные и конечные
параметры рабочего тела.
3) Вывести уравнение процесса,
устанавливающее связь между начальным и
конечным параметрами рабочего тела в
данном процессе.
4) Определить изменение внутренней энергии,
энтропии и величину работы изменения
объема газа.
34. Изохорный процесс
Изохорным называют процесс, протекающий принеизменном объеме рабочего тела.
p
0
1
(p1,T1)
2
(p2,T2)
v
1. Уравнение v=Const.
2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона:
v
p1v=RT1
и
p1/T1=p2/T2 или
p2v=RT2:
p/T=Const.
35. Изохорный процесс
v24. Работа l ( pdv) 0 , так как v=Const.
v1
5. Теплота: из I закона термодинамики –
или через теплоемкость –
6. Изменение внутренней энергии:
7. Изменение энтропии:
q=Δu;
q=CvΔT.
Δu=CvΔT.
ΔS=Cv ln(T2/T1)
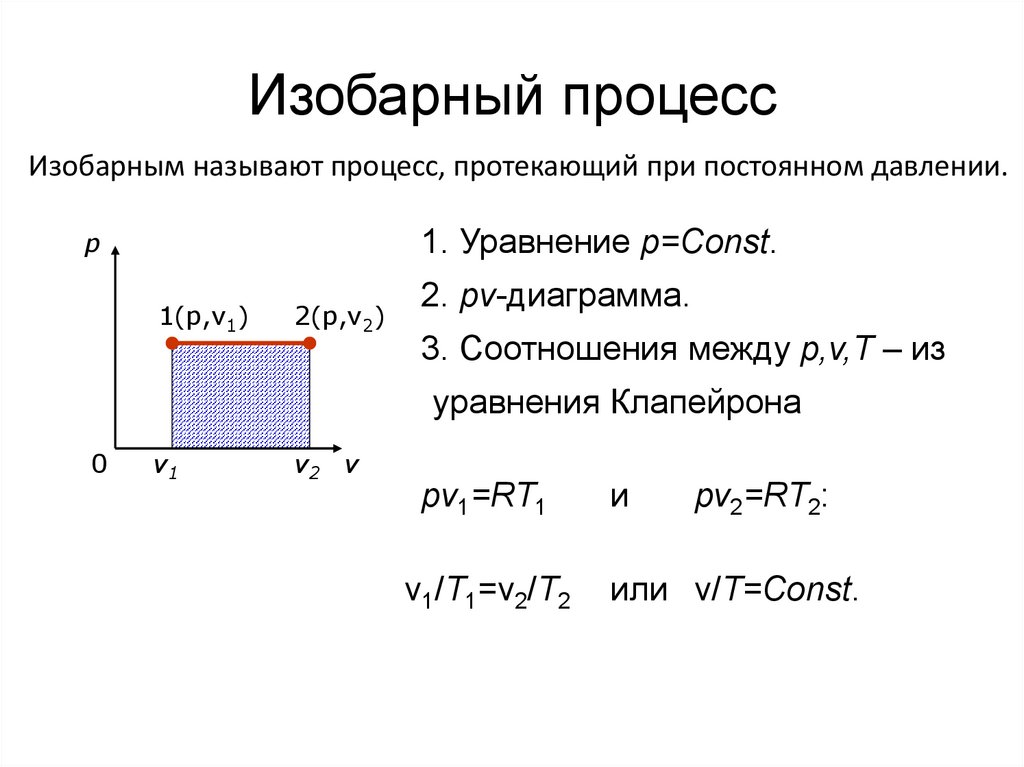
36. Изобарный процесс
Изобарным называют процесс, протекающий при постоянном давлении.1. Уравнение p=Const.
p
1(p,v1)
2(p,v2)
2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона
0
v1
v2 v
pv1=RT1
v1/T1=v2/T2
и
pv2=RT2:
или v/T=Const.
37. Изобарный процесс
v24. Работа: l ( pdv ) =p(v2-v1).
v1
5. Теплота: из I закона термодинамики – q=Δu+l
или через теплоемкость – q= Δh=cpΔT.
6. Изменение внутренней энергии:
Δu=cvΔT.
7. Изменение энтропии:
ΔS=Cp ln(T2/T1)
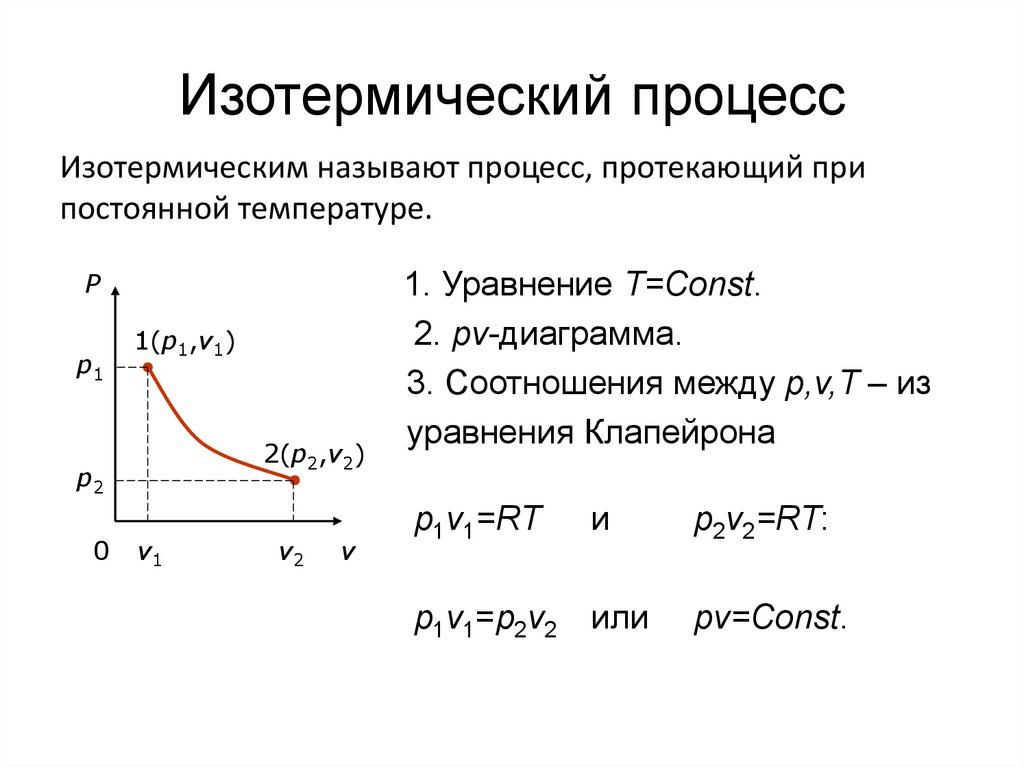
38. Изотермический процесс
Изотермическим называют процесс, протекающий припостоянной температуре.
P
p1
1(p1,v1)
2(p2,v2)
p2
0
v1
v2
v
1. Уравнение T=Const.
2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона
p1v1=RT
и
p1v1=p2v2 или
p2v2=RT:
pv=Const.
39. Изотермический процесс
4. Изменение внутренней энергии:Δu=cvΔT=0.
5. Работа:
6. Теплота: из I закона термодинамики:
q=l=RTln(p1/p2).
7. Изменение энтропии: ΔS=R ln(P1/P2)
40. Адиабатный процесс
Адиабатным называют процесс, происходящий безтеплообмена с окружающей средой
P
pv = Const
pvk = Const
p1
p2
0
1. Уравнение pvk=Const.
2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона
1(p1,v1)
p1v1=RT1
v1 v2a v2T v
p1vk1=p2vk2
и
p2v2=RT2:
T1V1k-1=p2T2k-1
где k – показатель адиабаты,
зависящий от природы газа
41. Адиабатный процесс
4. Работа:5. Изменение внутренней энергии:
Δu=Cv(T1-T2).
6. Теплота: из I закона термодинамики:
q=0=Δu+l.
7. Изменение энтропии: ΔS=0.
42. Политропный процесс
Политропными называют процессы протекающие припостоянной теплоемкости
1. Уравнение pvn=Const.
где n – показатель политропы, изменяющийся от - ∞ до
+∞.
2. Соотношения между p,v,T:
p1vn1=p2vn2
T1V1n-1=p2T2n-1
43. Политропный процесс
3. Работа:4. Изменение внутренней энергии:
Δu=Cv(T2-T1).
5. Теплота: из I закона термодинамики:
q=Cn(T2-T1),
где Cn – теплоемкость идеального газа в
политропном процессе.
6. Изменение энтропии: ΔS=Cn ln(T2/T1)
44. Обобщающее значение политропных процессов
Уравнение политропных процессов pvn=Const справедливодля любого из частных термодинамических процессов:
● изохорный
n=∞: p1/nv=p1/∞v=p0v=v=Const;
● изобарный
n=0: pv0=p=Const;
● изотермический
n=1: pv=Const или T=Const;
● адиабатный
n=k: pvk=Const.
45. PV- диаграмма политропных процессов
pn=-∞
v=Const
q>0
I
Δu>0
n=0
p=Const
Δu<0
q<0
II
III
n=+∞
v=Const
0
n=1
T=Const
n=k
pvk=Const
v
46. Ts - диаграмма политропных процессов
Tn=-∞
v=Const
n=0
p=Const
q<0
Δu>0
n=1
T=Const
Δu<0
q>0
n=+∞
v=Const
0
n=k
pvk=Const
s
47. ● Круговые процессы или циклы ● Цикл Карно ● II закон термодинамики
48. Термодинамические процессы
Самопроизвольные1. Проходят без затраты работы.
2. С их помощью можно получить
работу.
Несамопроизвольные
1. Проходят только с затратой работы.
2. С их помощью нельзя получить
работу.
Примеры:
- Теплота передается от горячего тела к холодному, но не наоборот;
- Вода самопроизвольно не разлагается на водород и кислород;
- Газ занимает весь предоставленный объем;
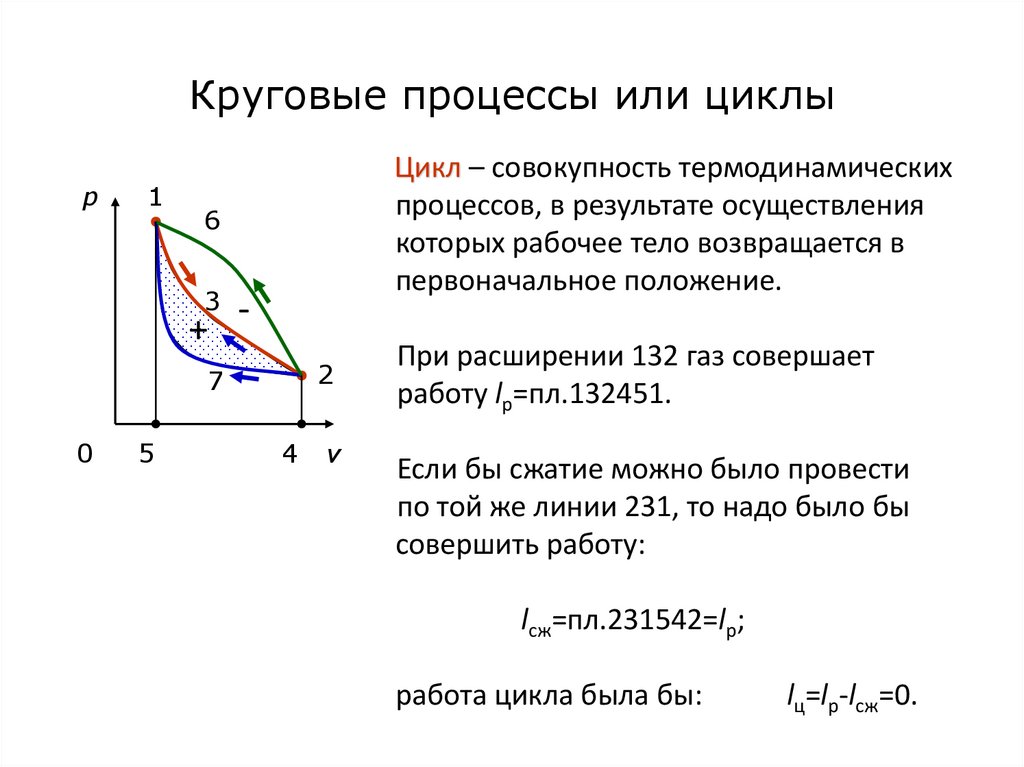
49. Круговые процессы или циклы
p1
Цикл – совокупность термодинамических
процессов, в результате осуществления
которых рабочее тело возвращается в
первоначальное положение.
6
3
+
2
7
0
5
4
v
При расширении 132 газ совершает
работу lp=пл.132451.
Если бы сжатие можно было провести
по той же линии 231, то надо было бы
совершить работу:
lсж=пл.231542=lр;
работа цикла была бы:
lц=lр-lсж=0.
50. Прямой цикл
В процессе сжатия 271 работа газа:(lсж=пл.271542)<(lp=пл.132451),
то есть работа цикла положительная: lц=lр-lсж=пл.13271.
Цикл 13271 совершается по часовой стрелке и называется
прямым циклом (теплового двигателя).
Исследования показали, что для получения положительной
работы цикла надо на одном его участке подвести к рабочему
телу теплоту q1 от горячего источника; на другом участке
отвести от рабочего тела теплоту q2 к холодному источнику.
51. Обратный цикл
В процессе сжатия 261 работа газа:(lсж=пл.261542)>(lp=пл.132451),
следовательно работа такого цикла отрицательная
lц=lр-lсж=пл.13261.
Цикл 13261 совершается против часовой стрелки и
называется обратным.
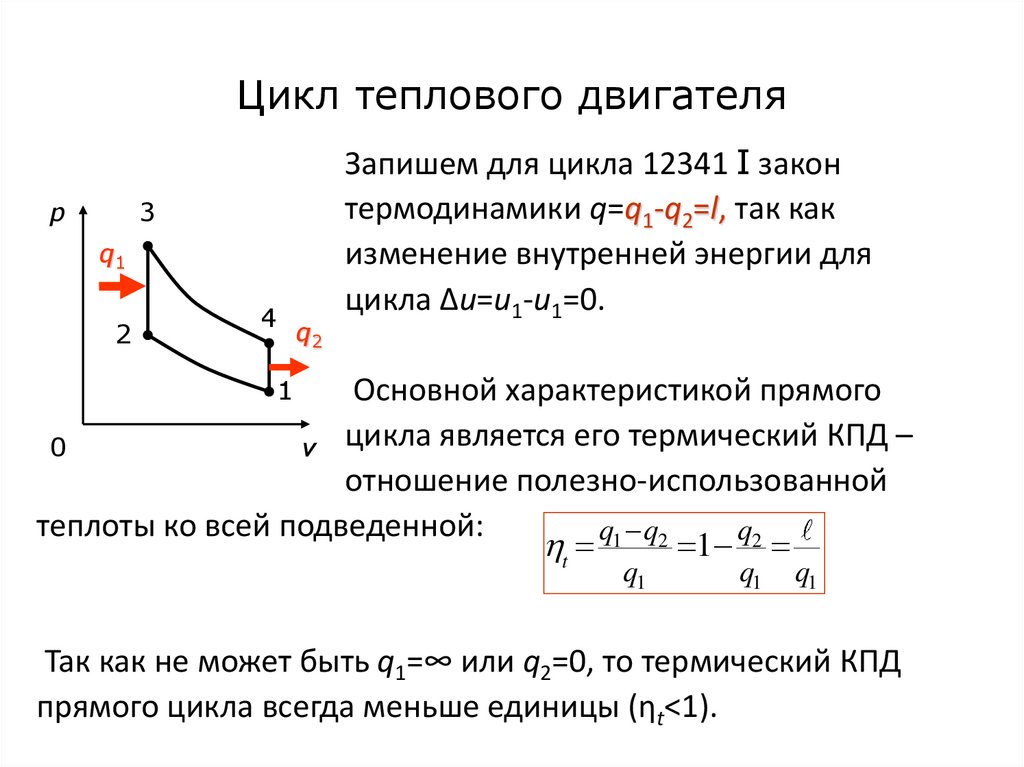
52. Цикл теплового двигателя
p3
q1
2
4
q2
Запишем для цикла 12341 I закон
термодинамики q=q1-q2=l, так как
изменение внутренней энергии для
цикла Δu=u1-u1=0.
1
Основной характеристикой прямого
0
v цикла является его термический КПД –
отношение полезно-использованной
теплоты ко всей подведенной:
t q1 q2 1 q2
q1
q1
q1
Так как не может быть q1=∞ или q2=0, то термический КПД
прямого цикла всегда меньше единицы (ηt<1).
53. Обратимые и необратимые циклы
Цикл называется обратимым, если он состоит только изобратимых процессов. Все реальные процессы необратимые,
поэтому реальные циклы также необратимы.
Термодинамика изучает обратимые циклы, необратимость
же учитывается эмпирическим коэффициентом.
Сади Карно в 1824 г. предложил оптимальный теоретический
цикл для преобразования теплоты в механическую энергию,
который невозможно осуществить в реальном тепловом двигателе
Значение цикла Карно заключается в том, что он имеет
максимальный КПД в заданном диапазоне температур.
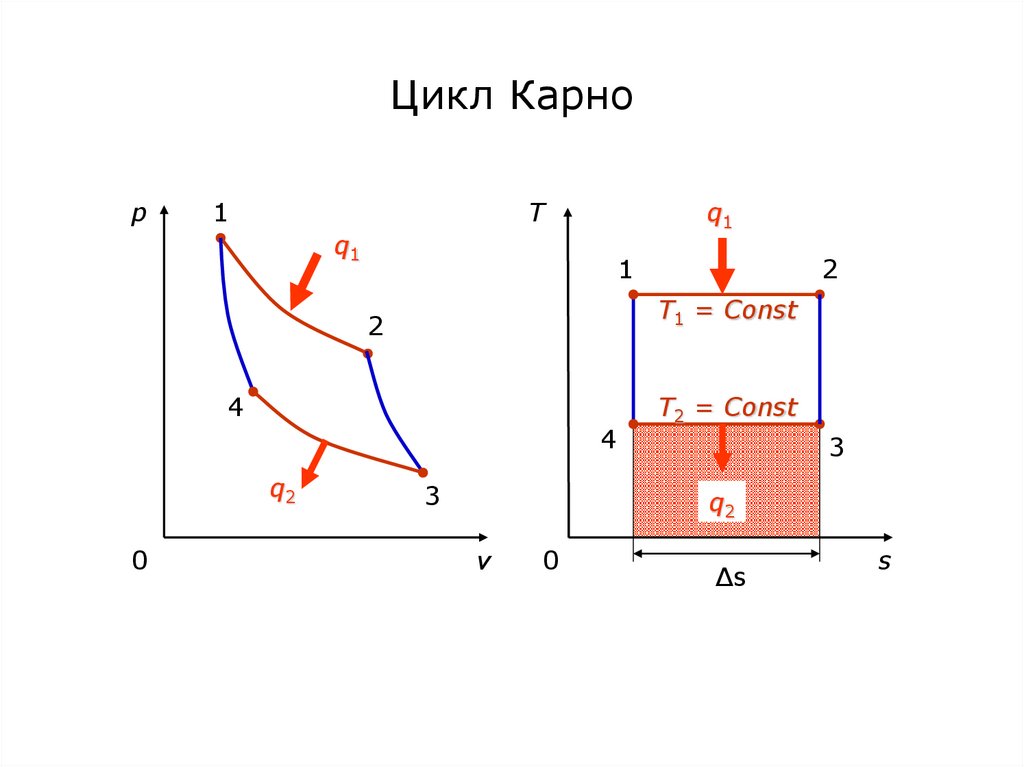
54. Цикл Карно
p1
T
q1
q1
1
T1 = Const
2
4
4
q2
0
2
3
T2 = Const
3
q2
v
0
Δs
s
55. Процессы, составляющие цикл Карно
1-2 изотермический подвод теплоты от энергоемкогогорячего источника к рабочему телу;
2-3 адиабатное расширение рабочего тела;
3-4 изотермический отвод теплоты от рабочего тела к
энергоемкому холодному источнику;
4-1 адиабатное сжатие рабочего тела.
Изотермический процесс самый экономичный для подвода
теплоты, так как в нем, согласно I закону термодинамики,
вся подведенная к газу теплота расходуется только на
работу (q=l).
56. Термический КПД цикла Карно
Адиабатный процесс расширения газа самый подходящий,так как в нем нет потерь теплоты от газа в окружающую
среду (q=0).
В Ts-диаграмме (тепловой) площадь под процессом
представляет собой теплоту, поэтому термический КПД
цикла Карно:
t 1 q2 1 T2 s 1 T2 T1 T2
q1
T1 s
T1
T1
57. Независимость ηt цикла Карно от физических свойств рабочего тела
В выражении термического КПД нет физических свойстврабочего тела.
Значит ηt цикла Карно зависит только от температур
горячего и холодного источников.
Причем, чем шире диапазон температур цикла, тем выше его
термический КПД.
58. Обратный цикл Карно
T1
q1
4
T1=Const
Обратный цикл Карно характеризует
совершенство передачи теплоты от
холодного источника к горячему.
T2=Const
2
3
1-2 адиабатное расширение рабочего
0
s тела;
2-3 изотермический подвод теплоты
от холодного источника к рабочему
телу;
3-4 адиабатное сжатие рабочего тела;
4-1 изотермический отвод теплоты от рабочего тела к
горячему источнику.
q2
59. Холодильный коэффициент
По I закону термодинамики для цикла:q= q1-q2=l.
Основной характеристикой обратного цикла является
холодильный коэффициент:
ε=q2/(q1-q2)=q2/l.
Для обратного цикла Карно:
ε=T2Δs/(T1Δs-T2Δs)=T2/(T1-T2).
60. Формулировки II закона термодинамики
● Карно: для преобразования тепловой энергии вмеханическую необходимы два источника теплоты – горячий
и холодный.
● Томсона: вся теплота, подведенная от горячего источника к
рабочему телу, не может быть преобразована в механическую
энергию; часть этой теплоты должна быть отдана холодному
источнику.
● Планка: невозможно реализовать вечный двигатель II рода.
● Клаузиуса: невозможно передать теплоту от холодного тела к
горячему самопроизвольно, то есть даровым способом.
61. II закон термодинамики
● Для обратимого процесса:∫ dq/T=0
● Для необратимого процесса:
∫ dq/T<0
где q – количество теплоты в процессе;
Т – абсолютная температура, при которой
подводится или отводится тепло.
62.
● Реальные газы● Уравнения состояний
● Водяной пар
63. Реальные газы
В реальных газах молекулы представляют собой упругиетела, имеют собственный объем и взаимодействуют между
собой.
Исторически первое уравнение состояния реальных газов
было получено Ван-Дер-Ваальсом.
Из уравнения состояния идеальных газов (Клапейрона)
pv=RT; v=RT/p,
то есть при p=∞: v=0,
что не соответствует действительности.
64. К выводу уравнения Ван-Дер-Ваальса
Обозначим собственный объем молекул реального газабуквой b,
тогда:
v-b=RT/p,
то есть при p=∞: (v-b)
0; v
b,
где b – константа Ван-Дер-Ваальса.
Выразим из полученного уравнения давление
p=RT/(v-b)
и учтем взаимодействие между молекулами.
65. Уравнение Ван-Дер-Ваальса
Давление – это результат ударов молекул о
стенки сосуда.
Притяжение других молекул ослабляет силу
удара молекулы на поправку Δp, которая пропорциональна
числу притягиваемых и притягивающих молекул,
то есть:
Δp=aρ2=a/v2,
где а – константа Ван-Дер-Ваальса.
C учетом этого:
p=RT/(v-b)-Δp=RT/(v-b)-a/v2.
66. Уравнения состояния реальных газов
Итак, уравнение состояния реальных газов Ван-Дер-Ваальса:( p a2 )(v b) RT
.
Ван-Дер-Ваальс учел только два фактора, отличающих
реальные газы от идеальных, поэтому его уравнение не очень
точное.
v
Более точным является уравнение Вукаловича-Новикова, в
котором учтены дополнительно ассоциация (объединение в
многомолекулярные комплексы) и диссоциация
(раздробление) комплексов:
.
a
c
(p
v
2
)(v b) RT (1
vT
(3 2m) / 2
)
67. Водяной пар
Водяной пар является рабочим телом паротурбинныхустановок (ПТУ).
Водяной пар – это реальный газ, состояние которого
можно описать уравнением состояния Вукаловича-Новикова.
Для удобства, состояния пара были просчитаны в большом
диапазоне параметров, а результаты представлены в виде
таблиц термодинамических свойств воды и пара и в форме
pv-, Ts-, hs-диаграмм.
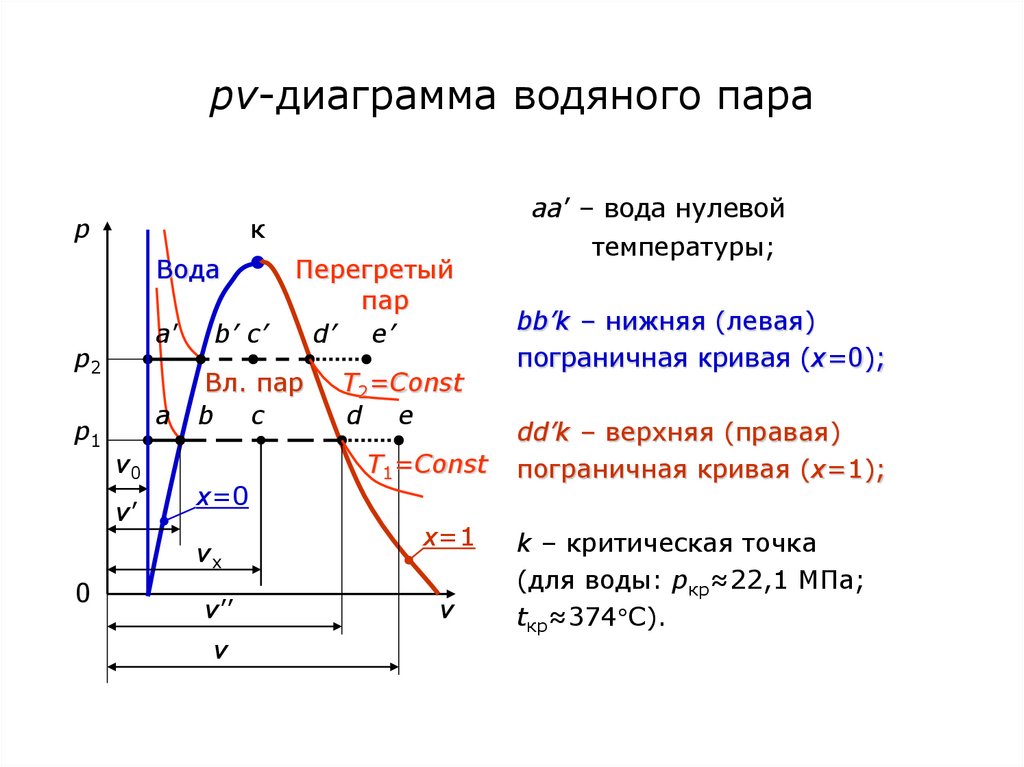
68. рv-диаграмма водяного пара
pк
Вода
a’
p2
p1
a
v0
v’
b’ c’
Перегретый
пар
d’ e’
Вл. пар
b c
x=0
vx
0
aa’ – вода нулевой
v’’
v
T2=Const
d e
T1=Const
x=1
v
температуры;
bb’k – нижняя (левая)
пограничная кривая (х=0);
dd’k – верхняя (правая)
пограничная кривая (х=1);
k – критическая точка
(для воды: pкр≈22,1 МПа;
tкр≈374 С).
69. К pv-диаграмме
Слева от пограничной кривой – вода;между пограничными кривыми – влажный пар;
правее верхней пограничной кривой – перегретый пар.
На верхней пограничной кривой – сухой, насыщенный пар.
Точка а(v0) – вода нулевой температуры;
процесс ab – изобарный нагрев воды от 0 С до температуры
кипения (насыщения) tн;
70. Процессы и состояния воды и пара
На верхней пограничной кривой – сухой, насыщенный пар.Точка а (v0) – вода нулевой температуры;
процесс ab – изобарный нагрев воды от 0 С до температуры
насыщения tн (кипения);
точка b (v’; х=0) – вода на линии насыщения (закипающая);
процесс bd – изобарно-изотермическое парообразование
(кипение воды) при tн=Const;
точка d (v”; х=1) – сухой, насыщенный пар;
71. Влажный и перегретый пар
точка c – влажный, насыщенный пар (х – степень сухостипара: массовая доля пара во влажном паре);
процесс de – изобарный перегрев пара;
точка e (v) – перегретый пар.
Начало отсчета внутренней энергии u0=0; энтальпии h0=0
и энтропии s0=0 примем при 0 С (273 К) – точка а.
Процесс abcde при p=Const тот же, что был описан в
pv-диаграмме.
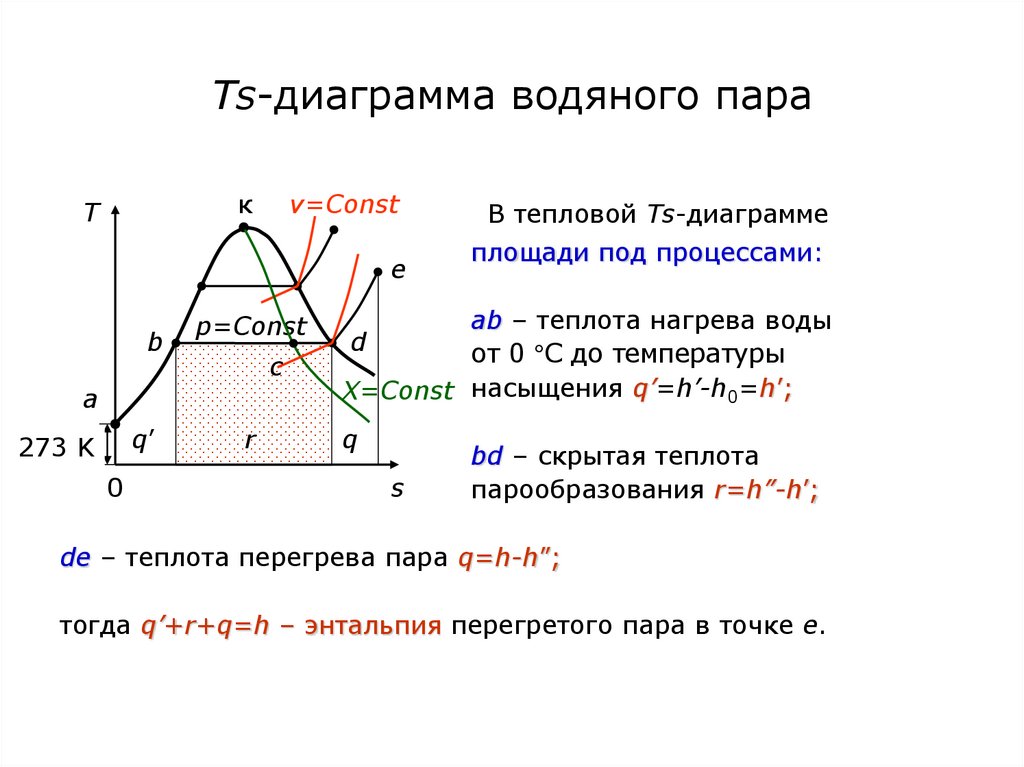
72. Ts-диаграмма водяного пара
кT
v=Const
e
b
p=Const
c
a
q’
273 K
0
r
В тепловой Ts-диаграмме
площади под процессами:
аb – теплота нагрева воды
d
от 0 С до температуры
X=Const насыщения q’=h’-h0=h’;
q
s
bd – скрытая теплота
парообразования r=h”-h’;
de – теплота перегрева пара q=h-h”;
тогда q’+r+q=h – энтальпия перегретого пара в точке е.
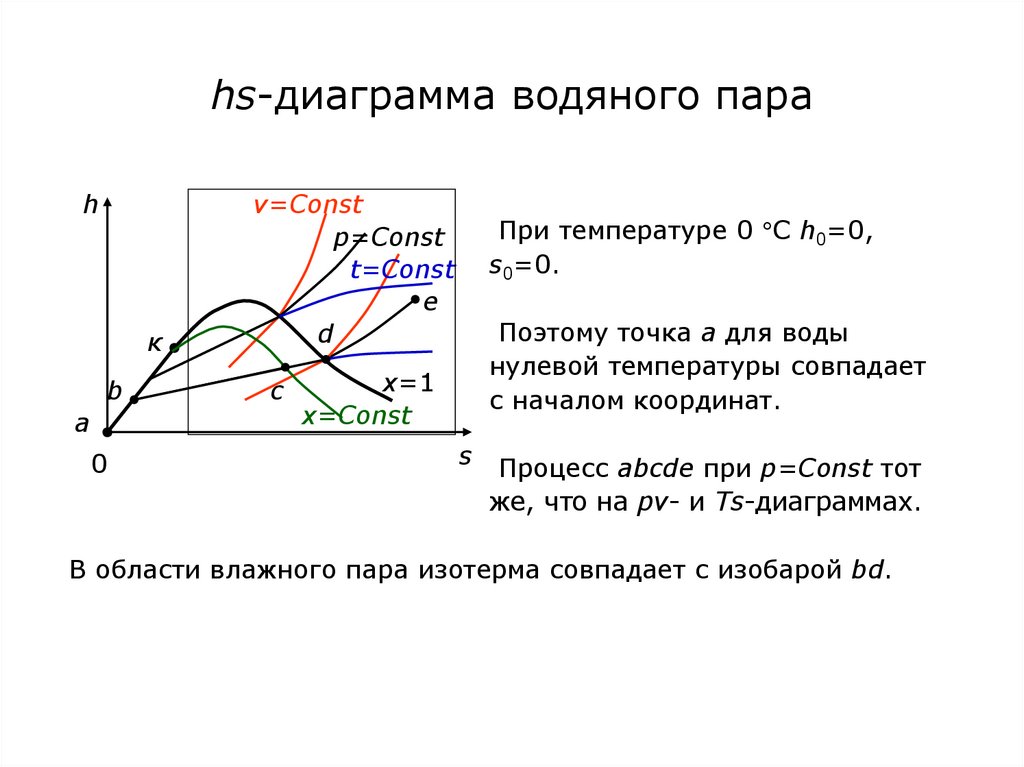
73. hs-диаграмма водяного пара
hк
b
a
0
v=Const
p=Const
t=Const
e
d
c
x=1
x=Const
При температуре 0 С h0=0,
s0=0.
Поэтому точка а для воды
нулевой температуры совпадает
с началом координат.
s Процесс abcde при p=Const тот
же, что на pv- и Ts-диаграммах.
В области влажного пара изотерма совпадает с изобарой bd.
74. Расчеты процессов водяного пара
В практических расчетах обычно используются областиперегретого пара и влажного с высокими степенями сухости.
Поэтому изображается в большем масштабе выделенная
рамкой часть диаграммы.
Более точные расчеты процессов водяного пара выполняется
по таблицам.
75. Таблицы термодинамических свойств воды и водяного пара
Бывают таблицы термодинамических свойств водына линии насыщения и сухого, насыщенного пара
(tн, v’, v”, h’, h”, r, s’, s”)=f(pн)
(pн, v’, v”, h’, h”, r, s’, s”),=f(tн)
где
pн, tн – давление и температура насыщения;
v, h, s – удельный объем, энтальпия и энтропия;
индексы ’, ” относятся к воде на линии насыщения и
сухому, насыщенному пару.
Таблицы термодинамических свойств перегретого пара
(v, h, s)=f (p, t).
76. Внутренняя энергия
В таблицах и диаграммах нет внутренней энергии воды и пара.Она находится через энтальпию, Дж/кг:
u’=h’-pv’;
ux=hx-pvx;
u”=h”-pv”;
u=h-pv,
где давление подставляется в Па.
77. Влажный пар
Параметры состояния влажного пара находятся по смесевымформулам:
vx=v’(1-x)+v”x;
hx=h’(1-x)+h”x;
sx=s’(1-x)+s”x.
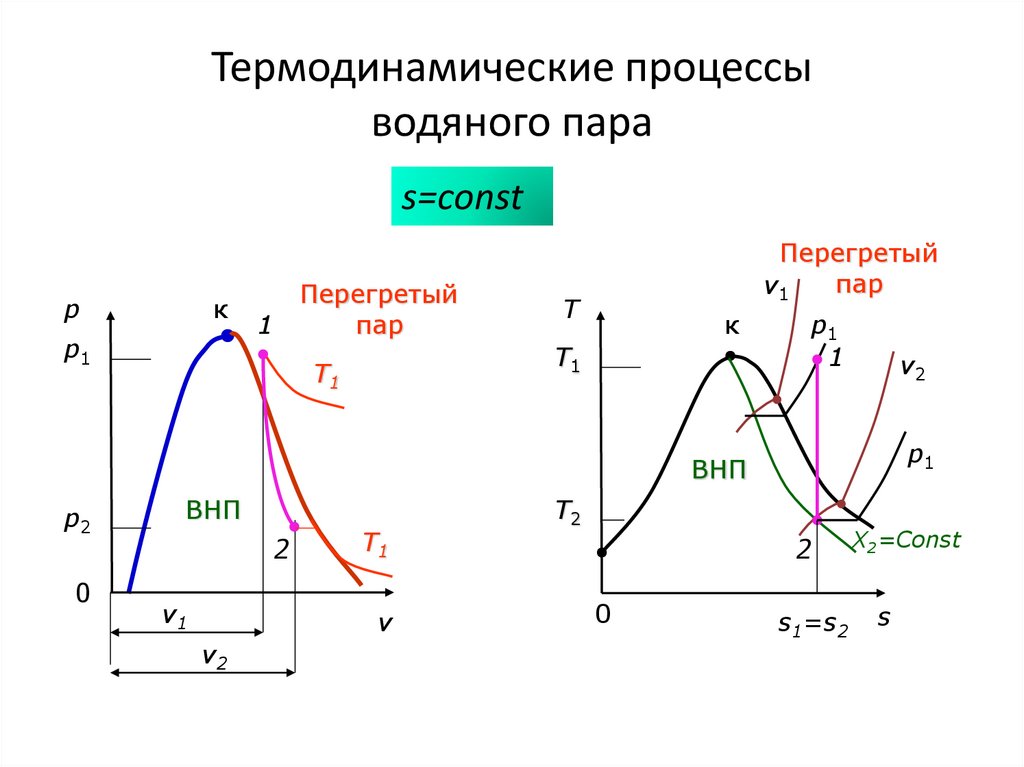
78. Термодинамические процессы водяного пара
v=сonstp
к
p2
2
T2=Const
Вл. пар
p1
0
Перегретый
пар
1
x=0
v1=v2
x=1
Перегретый
пар
T
к
T2
v=Const
2
p1
1
T1
Вл. пар
T1=Const
v
p2
0
X1=Const
s
79. Термодинамические процессы водяного пара
v=сonstI закон термодинамики:
u u2 u1 (h2 p2v2 ) (h1 p1v1 )
l 0
q u2 u1
80. Термодинамические процессы водяного пара
p=сonstp
к
Перегретый
пар
Перегретый
пар
T
к
2
T2
Вл. пар
p=const
1
x=1
0
v1
v2
p1=p2
T1
2
1
Вл. пар
T2=Const
x=0
v1
X1=Const
T1=Const
v2
v
0
s
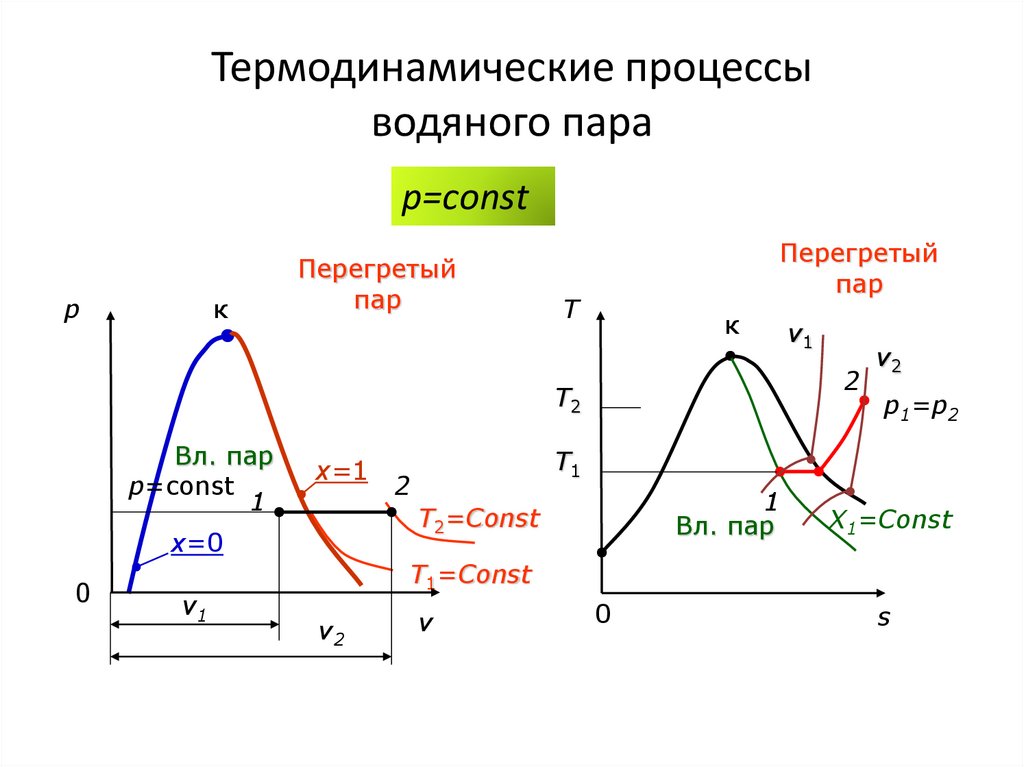
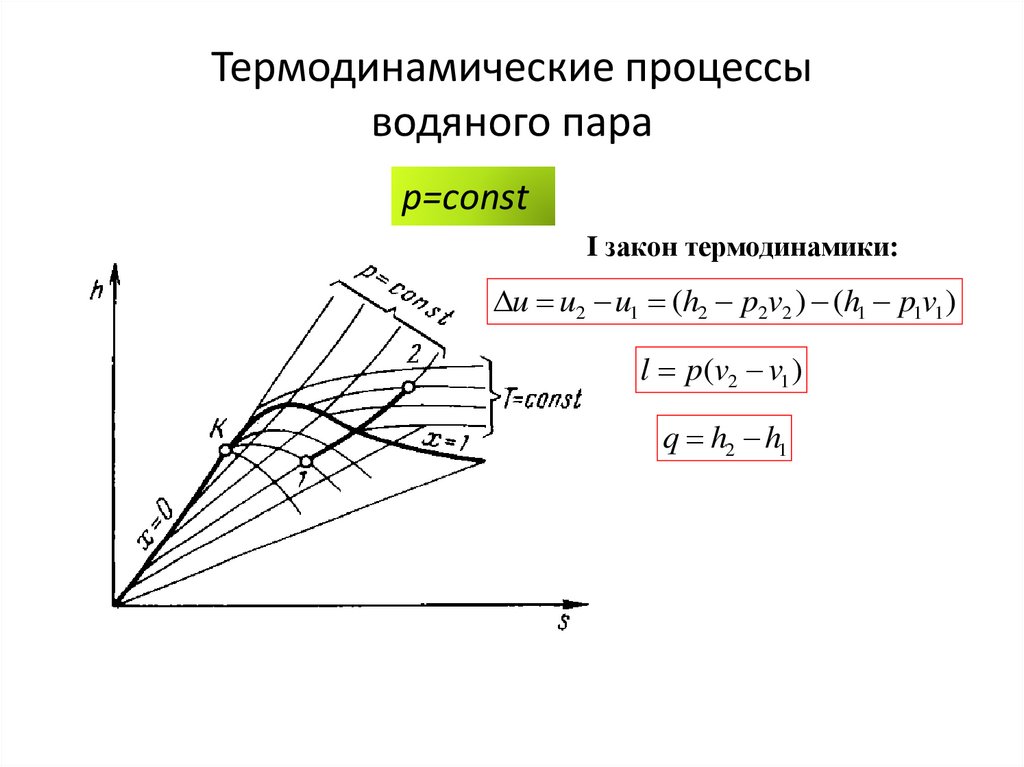
81. Термодинамические процессы водяного пара
p=сonstI закон термодинамики:
u u2 u1 (h2 p2v2 ) (h1 p1v1 )
l p(v2 v1 )
q h2 h1
82. Термодинамические процессы водяного пара
T=сonstp
p1
p2
к
Перегретый
пар
Перегретый
пар
v1
T
к
T=const
1
v1
2
Вл. пар
v2
v
p1
1
Вл. пар T=const
2
x=0
0
p1 v2
0
X1=Const
s
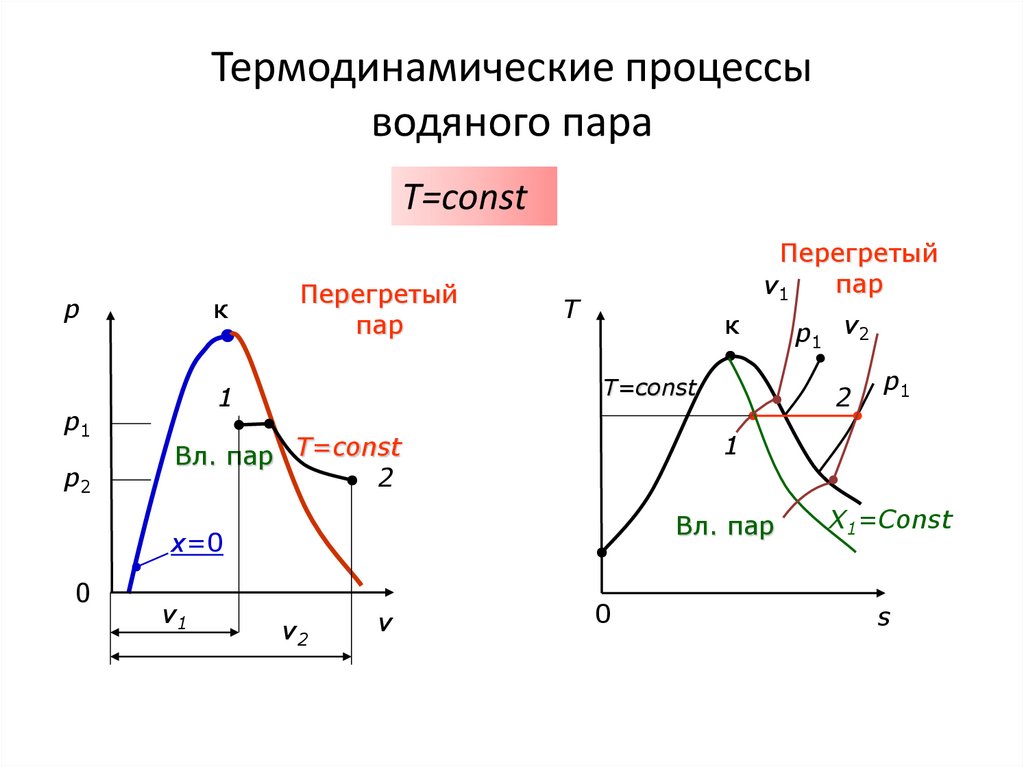
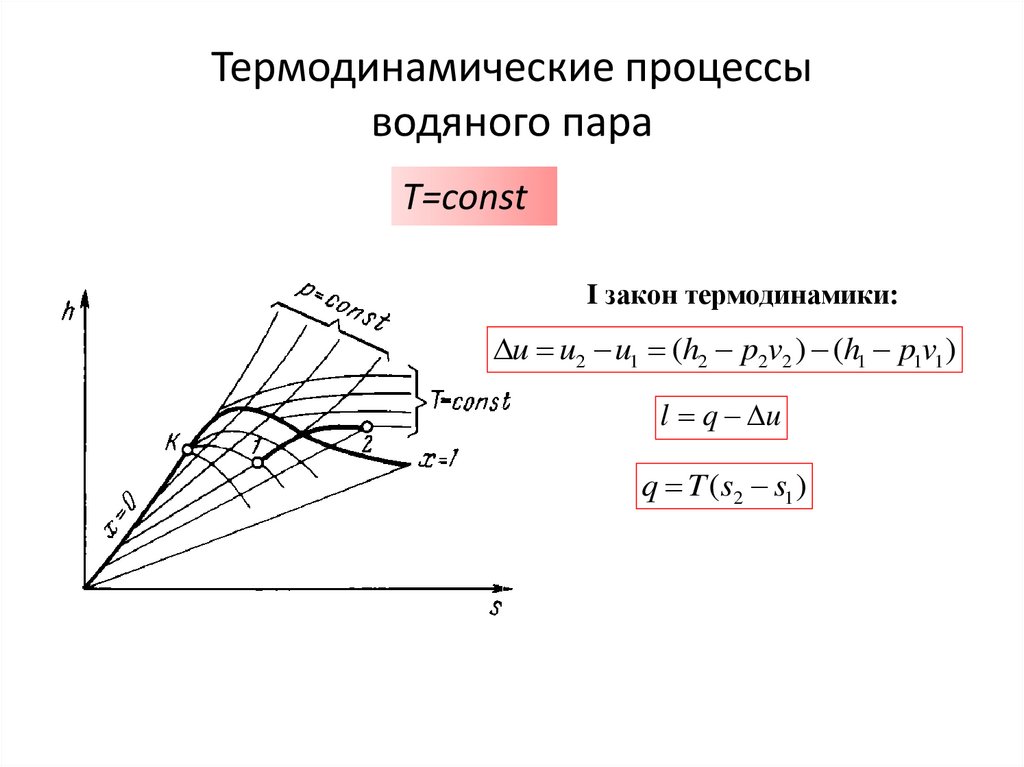
83. Термодинамические процессы водяного пара
T=сonstI закон термодинамики:
u u2 u1 (h2 p2v2 ) (h1 p1v1 )
l q u
q T (s2 s1 )
84. Термодинамические процессы водяного пара
s=сonstp
к
p1
1
Перегретый
пар
Перегретый
пар
v1
T
к
T1
T1
p1
1
v2
p1
ВНП
p2
0
ВНП
2
v1
T1
v
v2
T2
2
0
s1=s2
X2=Const
s
85. Термодинамические процессы водяного пара
s=сonstI закон термодинамики: l u u1 u2 (h1 p1v1 ) (h2 p2v2 )
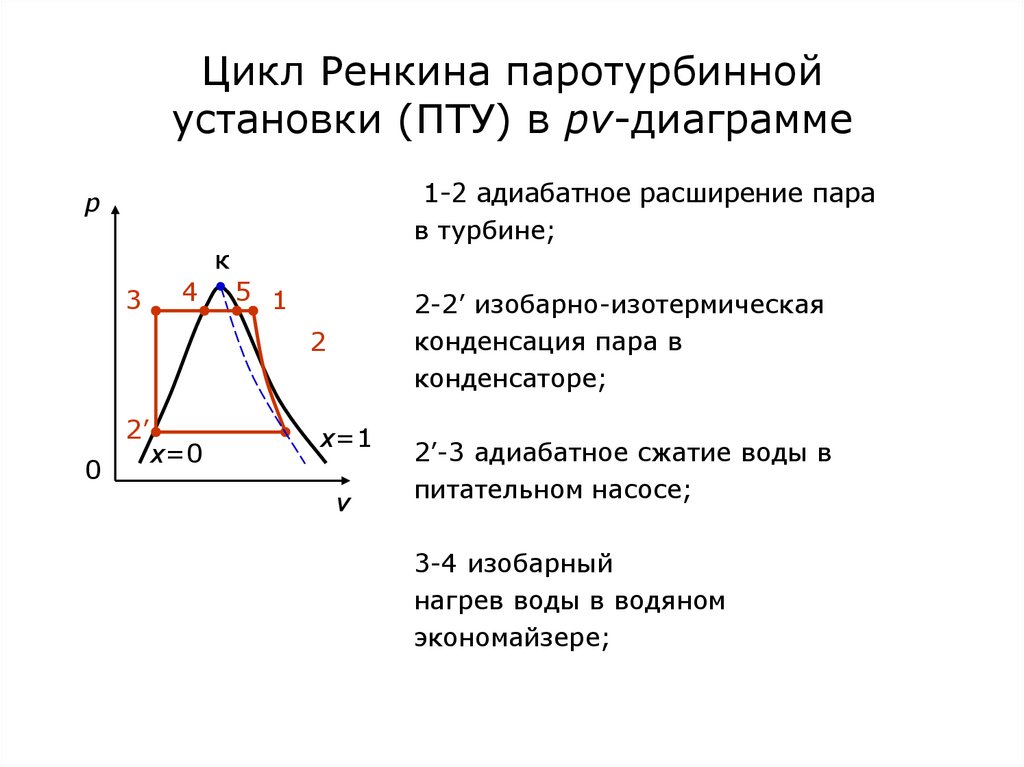
86. Цикл Ренкина паротурбинной установки (ПТУ) в pv-диаграмме
1-2 адиабатное расширение парав турбине;
p
к
3
4
5 1
2-2’ изобарно-изотермическая
конденсация пара в
конденсаторе;
2
2’
0
x=0
x=1
v
2’-3 адиабатное сжатие воды в
питательном насосе;
3-4 изобарный
нагрев воды в водяном
экономайзере;
87. Цикл Ренкина паротурбинной установки в Ts-диаграмме
4-5 изобарно-изотермическоепарообразование;
T
4
к
5
5-1 изобарный перегрев пара
в пароперегревателе.
1
Термический КПД цикла Ренкина:
3
0
2’
2
x=Const
s
t q1 q2 (h1 h3 ) (h2 h2' )
q1
h1 h3
.
(1)
88. Приближенный КПД цикла Ренкина
Если в выражении (1) перегруппировать члены, то:t (h1 h2 ) (h3 h2' )
h1 h3
т н.
q1
Здесь lт – положительная работа пара в турбине; lн – затрата
работы на сжатие воды в насосе; q1 – теплота, подведенная
к рабочему телу в парогенераторе.
В современных ПТУ lт≈1200-1600 кДж/кг, lн≈20-40 кДж/кг
и для приближенных расчетов работой сжатия воды можно
пренебречь, то есть считать,
т h1 h2
что h2’≈h3, тогда:
.
(2)
t
q1
h1 h2'
89. Цикл ПТУ с промперегревом
ПЕПП
ЦВД
ЦСД После расширения пара в ЦВД
до линии х=1 он поступает в
промежуточный пароперегреватель ПП, перегревается снова
в ЦНД до температуры свежего пара.
ПГ
к
T
4
1
7
5
6
3
2’
0
2
На цикле 6-7 промперегрев;
1-6 адиабатное расширение
пара в ЦВД, 7-2 – то же в ЦСД
и ЦНД.
x2P=Const x2п=Const Благодаря промперегреву
х2п>х2Р, поэтому ηtп>ηtр.
s











































































 physics
physics








