Similar presentations:
Теплоемкости газов. Термодинамические процессы
1. ТНиС 03
● Теплоемкости газов● Термодинамические процессы
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
1
2. Теплоемкости газов
Теплоемкость – это теплота, которую надо подвести кединичному количеству вещества, чтобы увеличить его
температуру на 1 К.
Различают теплоемкости:
● массовую
● объемную
c, Дж/(кг·К)
c’, Дж/(м³·К)
–
–
● мольную (μс), Дж/(кмоль·К) –
Q=mcΔT;
Q=V0c’ΔT;
Q=M(μс)ΔT,
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
2
3. Соотношения между теплоемкостями
гдеQ
m
V0
M
– теплота, Дж;
– масса газа, кг;
– объем газа при нормальных физических
условиях, м³;
– число кило молей газа.
Соотношения между теплоемкостями:
c=(μс)/μ;
c’=(μс)/(μv)0=(μс)/22,4;
c’=cρ0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
3
4. Теплоемкости смесей газов
Чтобы повысить температуру смеси газов на ΔT К, надона столько же нагреть каждый из ее компонентов:
n
cm T (ci mi ) T
1
n
;
c 'V0 T (c 'i V0i ) T
1
.
Поделим:
каждое уравнение на ΔT;
левое выражение на массу смеси m;
правое – на объем смеси при нормальных условиях V0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
4
5. Массовая, объемная и мольная теплоемкости
Учтем, что:mi /m=gi – массовая доля компонента;
V0i /V0=ri – объемная доля компонента.
Тогда соответственно массовая, объемная и мольная
теплоемкости смеси:
n
c (ci gi )
1
;
n
c ' (c 'i ri )
1
;
n
( c) ( c)i ri
.
1
Два последних выражения похожи, так как мольная
и объемная доли равнозначны.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
5
6. I закон термодинамики для изохорного и изобарного процессов
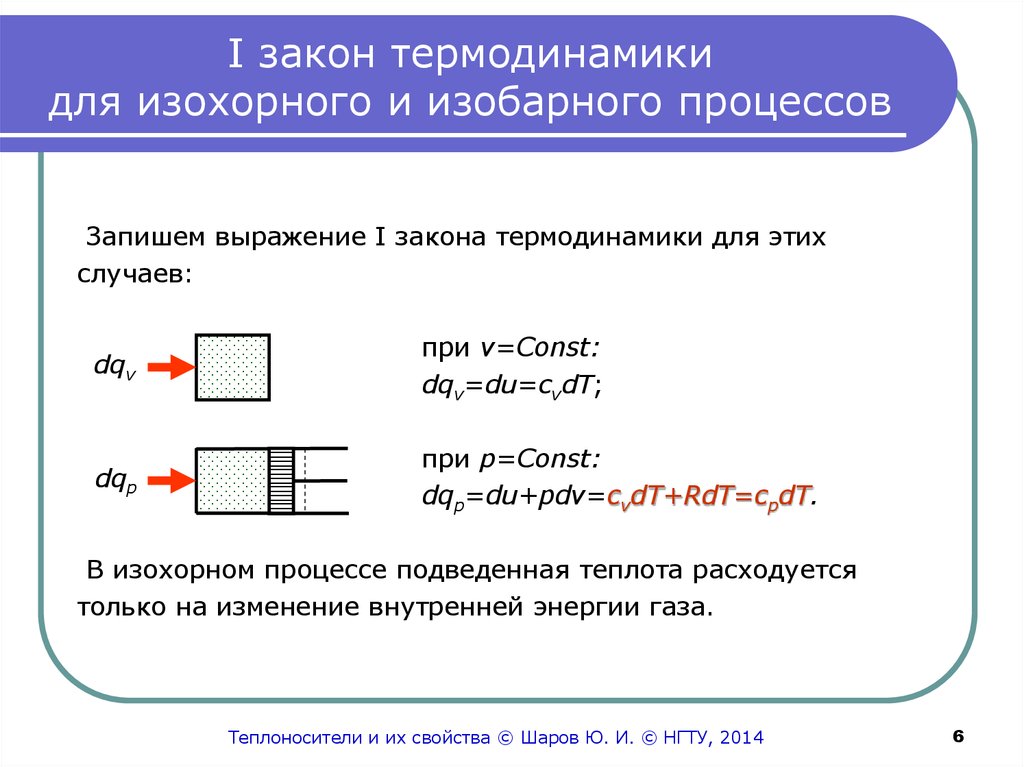
Запишем выражение I закона термодинамики для этихслучаев:
dqv
при v=Const:
dqv=du=cvdT;
dqp
при p=Const:
dqp=du+pdv=cvdT+RdT=cpdT.
В изохорном процессе подведенная теплота расходуется
только на изменение внутренней энергии газа.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
6
7. Теплоемкости cp и cv
В изобарном процессе подведенная теплота расходуетсяна изменение внутренней энергии газа и на совершение
работы против внешних сил.
Сократив на dT последнее равенство, получим соотношение
между этими теплоемкостями (уравнение Майера):
для 1 кг газа
для 1 кмоля газа
–
–
cp=cv+R
(μcp)=(μcv)+(μR).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
7
8. Показатель адиабаты
А отношение теплоемкостей cp и cv– показатель адиабаты:k=cp /cv.
Одноатомные газы:
k=1,67;
двухатомные газы:
k=1,41;
трех- и многоатомные газы:
k=1,29.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
8
9. Истинная теплоемкость
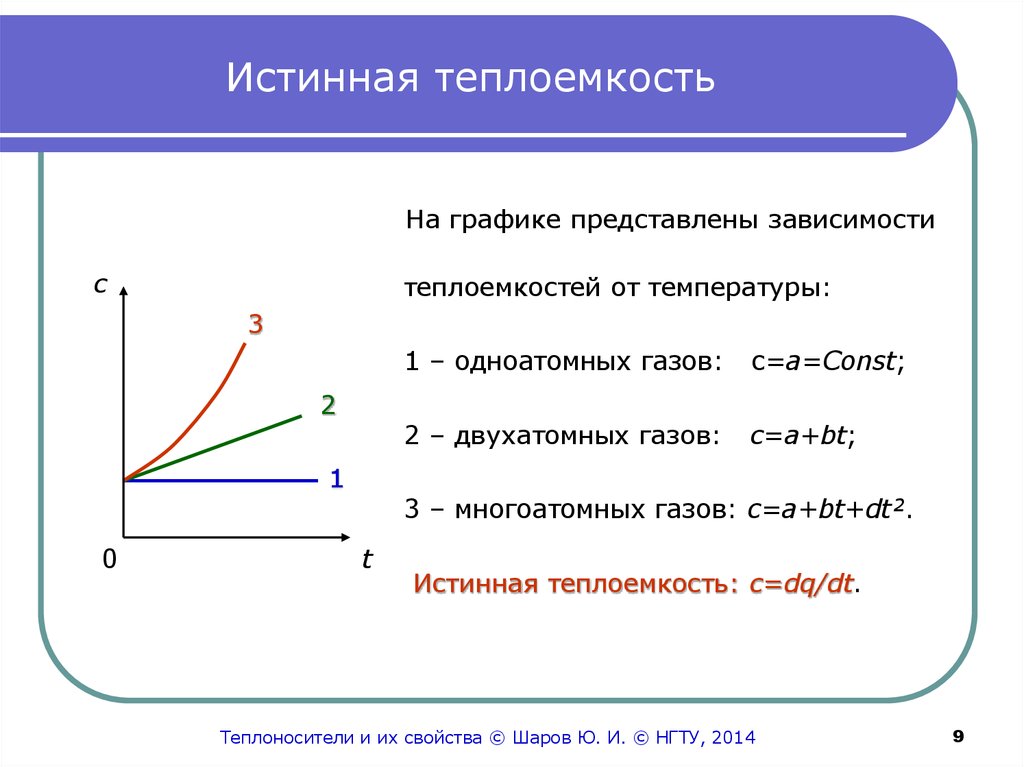
На графике представлены зависимостис
теплоемкостей от температуры:
3
2
1 – одноатомных газов:
c=a=Const;
2 – двухатомных газов:
c=a+bt;
1
3 – многоатомных газов: c=a+bt+dt².
0
t
Истинная теплоемкость: c=dq/dt.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
9
10. Средняя теплоемкость двухатомных газов
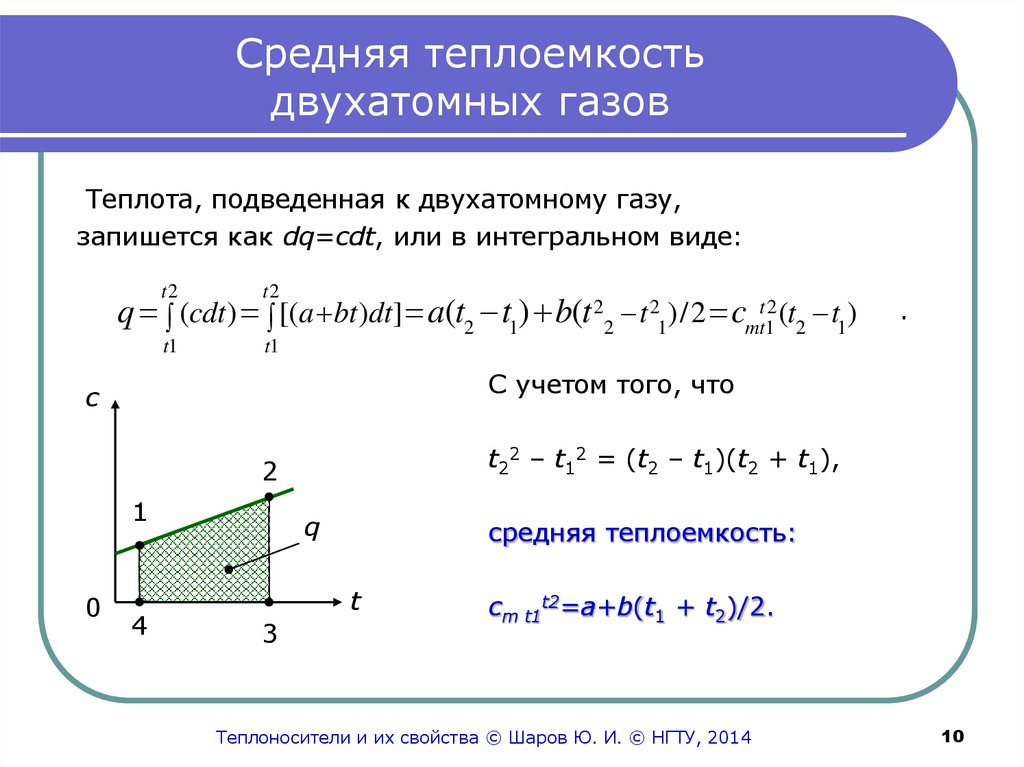
Теплота, подведенная к двухатомному газу,запишется как dq=cdt, или в интегральном виде:
t2
t2
t1
t1
q (cdt) [(a bt)dt] a(t2 t1) b(t 22 t 21)/2 cmtt12 (t2 t1)
С учетом того, что
с
t22 – t12 = (t2 – t1)(t2 + t1),
2
1
0
.
4
q
средняя теплоемкость:
t
3
cm t1t2=a+b(t1 + t2)/2.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
10
11. Определение теплоемкостей по формулам и таблицам
На предыдущих слайдах были приведены формулыистинных и средних теплоемкостей газов, в которых
константы a, b, d для каждого газа можно найти в
справочниках.
В справочниках также приводятся посчитанные по этим
формулам значения истинных (при температуре t) и
средних теплоемкостей разных газов в диапазоне
температур от 0 до t.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
11
12. Табличные теплоемкости
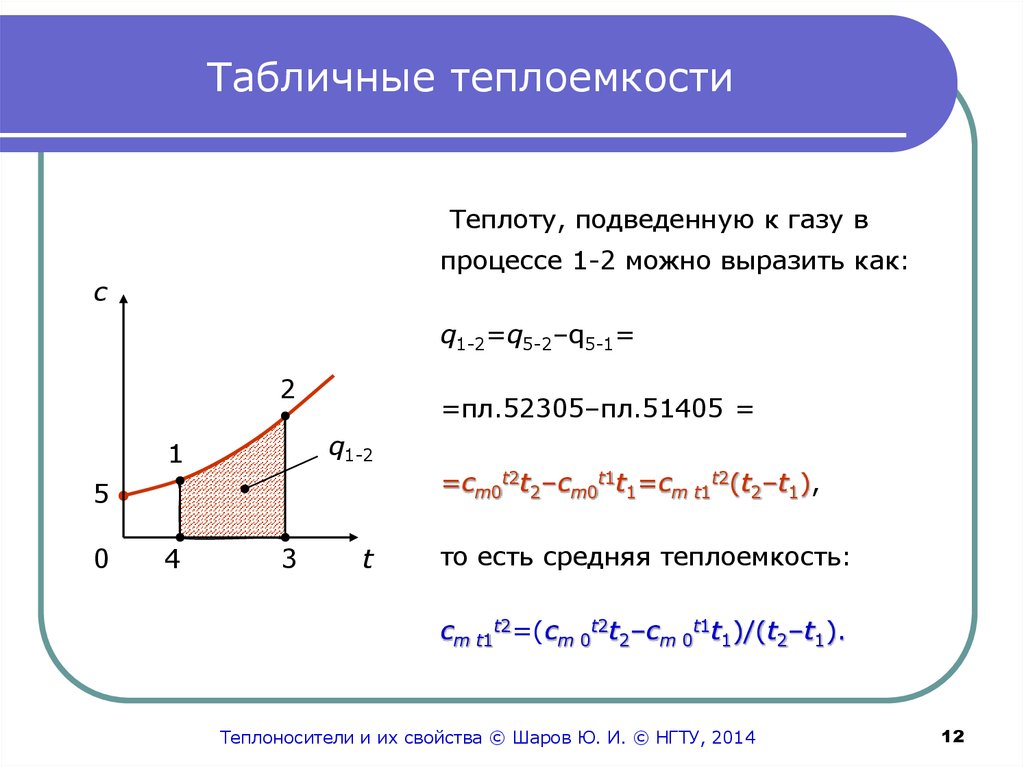
Теплоту, подведенную к газу впроцессе 1-2 можно выразить как:
с
q1-2=q5-2–q5-1=
2
=пл.52305–пл.51405 =
q1-2
1
=cm0t2t2–cm0t1t1=cm t1t2(t2–t1),
5
0
4
3
t
то есть средняя теплоемкость:
cm t1t2=(cm 0t2t2–cm 0t1t1)/(t2–t1).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
12
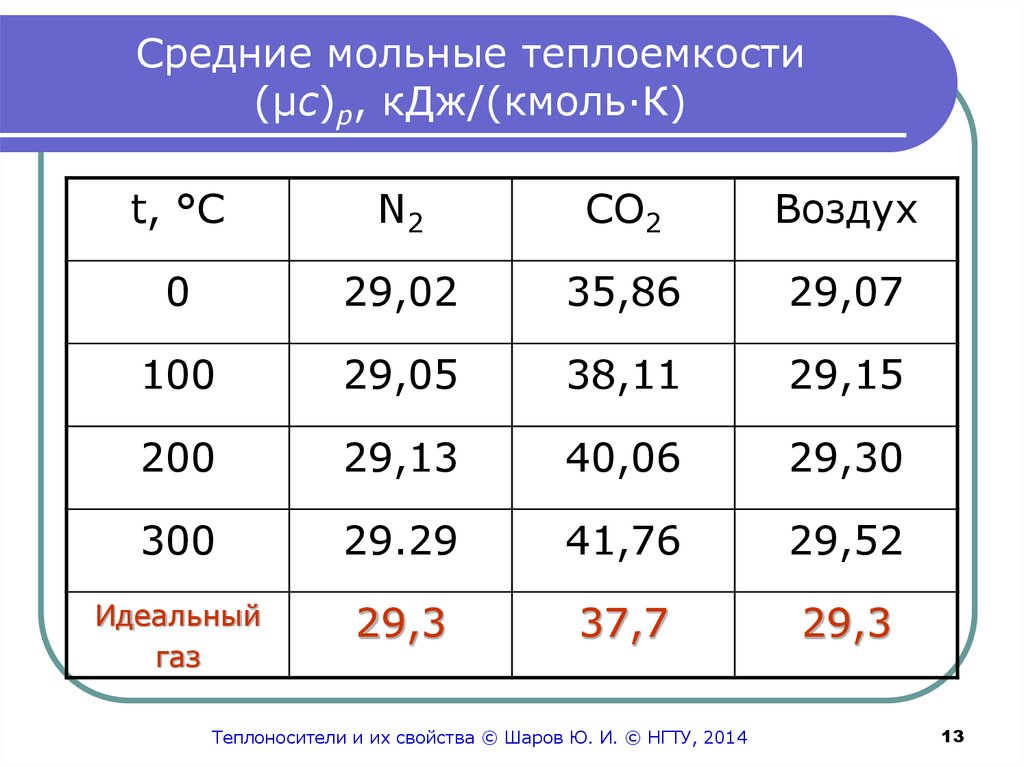
13. Средние мольные теплоемкости (μс)р, кДж/(кмоль·К)
t, °CN2
CO2
Воздух
0
29,02
35,86
29,07
100
29,05
38,11
29,15
200
29,13
40,06
29,30
300
29.29
41,76
29,52
Идеальный
газ
29,3
37,7
29,3
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
13
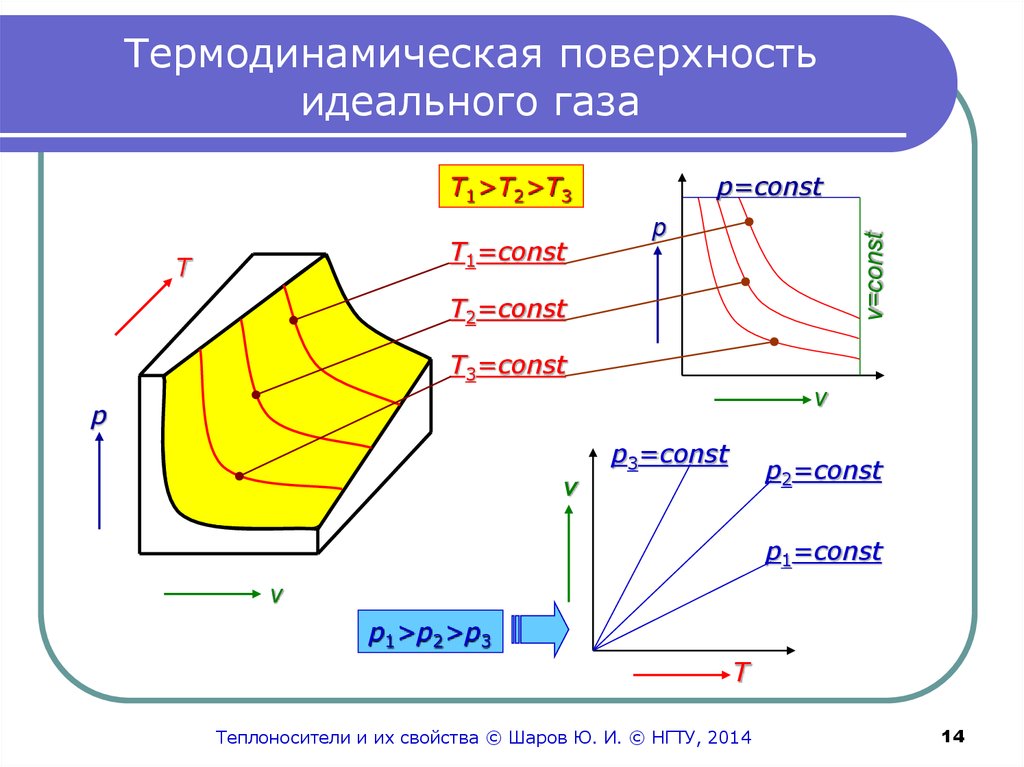
14. Термодинамическая поверхность идеального газа
T1>T2>T3p
v=const
T1=const
T
p=const
T2=const
T3=const
v
p
v
p3=const
p2=const
p1=const
v
p1>p2>p3
T
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
14
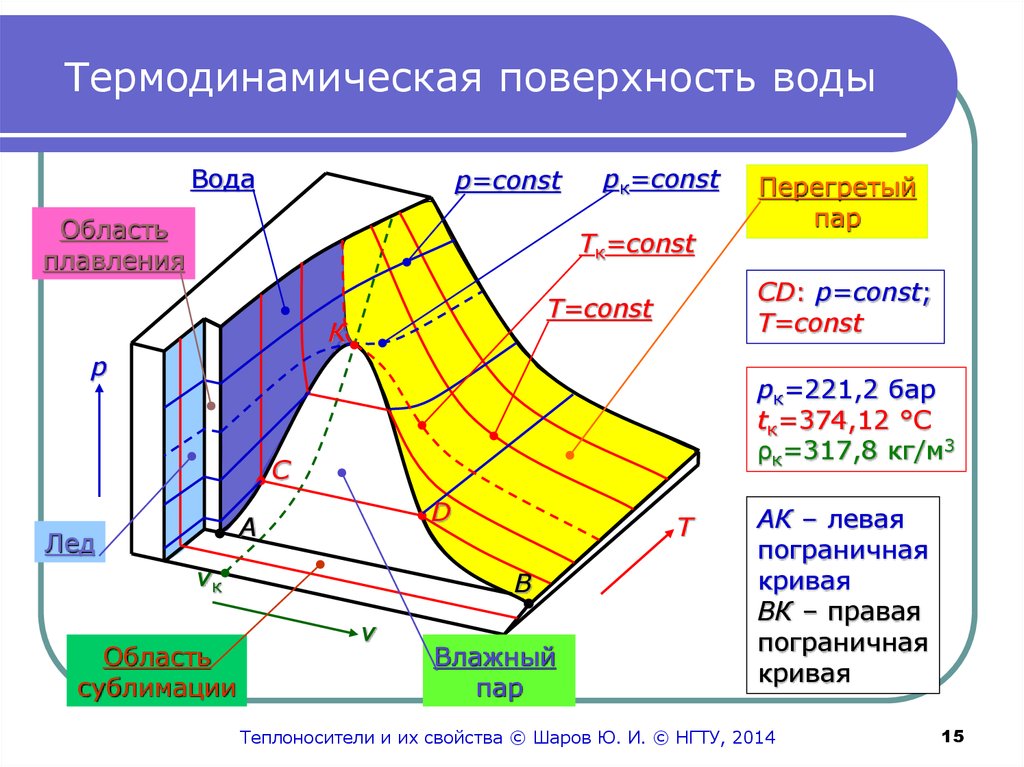
15. Термодинамическая поверхность воды
Водаp=const
Область
плавления
pк=const
Tк=const
СD: p=const;
T=const
T=const
К
р
рк=221,2 бар
tк=374,12 °С
ρк=317,8 кг/м3
С
D
А
Лед
vк
Область
сублимации
Перегретый
пар
Т
В
v
Влажный
пар
АК – левая
пограничная
кривая
ВК – правая
пограничная
кривая
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
15
16. Термодинамические процессы
Изохорный – процесс при неизменном объеме газа:v=сonst.
Изобарный – при постоянном давлении газа:
p=сonst.
Изотермический – при постоянной температуре газа:
T=сonst.
Адиабатный – без теплообмена между газом и
окружающей средой:
q=0.
Политропный – процесс без ограничений.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
16
17. Исследование термодинамических процессов
Чтобы выявить основные закономерности изменениясостояния газа и особенностей превращения энергии,
выполняется исследование термодинамических процессов
по единой методике:
1. Выводится уравнение процесса;
2. Приводится pv-диаграмма процесса;
3. Выводятся соотношения между параметрами p,v,T;
4. Определяется изменение внутренней энергии газа по
единой формуле, Дж/кг:
Δu=cvΔT;
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
17
18. Методика исследования термодинамических процессов
v25. Находится работа газа против внешних сил
6. Определяется теплота, подведенная к газу:
l ( pdv )
.
v1
● по I закону термодинамики
q=Δu+l;
● или через теплоемкость
q=c(t2-t1),
где c – массовая теплоемкость газа в данном процессе;
7. Находится энергетический коэффициент φ=Δu/q,
показывающий долю теплоты, затраченной на изменение
внутренней энергии.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
18
19. Исследование изохорного процесса
p0
1
(p1,T1)
2
(p2,T2)
v
1. Уравнение v=сonst.
2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона:
v
p1v=RT1
и
p2v=RT2:
p1/T1=p2/T2
или
p/T=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
19
20. Изохорный процесс
4. Изменение внутренней энергии:Δu=cvΔT.
v2
5. Работа
l ( pdv) 0 , так как v=сonst.
v1
6. Теплота: из I закона термодинамики –
или через теплоемкость
–
q=Δu;
q=cvΔT.
7. Энергетический коэффициент:
φ=Δu/q=1.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
20
21. Исследование изобарного процесса
1. Уравнение p=сonst.p
2. pv-диаграмма.
1(p,v1)
2(p,v2)
3. Соотношения между p,v,T – из
уравнения Клапейрона
0
v1
v2 v
pv1=RT1
и
pv2=RT2:
v1/T1=v2/T2
или
v/T=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
21
22. Изобарный процесс
4. Изменение внутренней энергии: Δu=cvΔT.5. Работа:
v2
l ( pdv )
=p(v2-v1)=R(T2-T1).
v1
6. Теплота:
из I закона термодинамики
–
q=Δu+l
или через теплоемкость
–
q=cpΔT.
7. Энергетический коэффициент:
φ=Δu/q=cvΔT/cpΔT=1/k.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
22
23. Преобразование выражения I закона термодинамики
Запишем выражение I закона термодинамики и преобразуемего следующим образом:
dq=du+pdv+vdp-vdp=
=du+d(pv)-vdp=d(u+pv)-vdp.
Обозначим (u+pv)=h и назовем ее энтальпией, Дж/кг.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
23
24. Параметр состояния энтальпия
Тогда можно записать аналитическое выражение I законатермодинамики через энтальпию:
dq=dh-vdp.
Здесь h=u+pv=cvT+RT=(cv+R)T=cpT,
то есть энтальпия – это теплота, необходимая для
нагревания 1 кг газа от 0 до Т, К в изобарном процессе.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
24
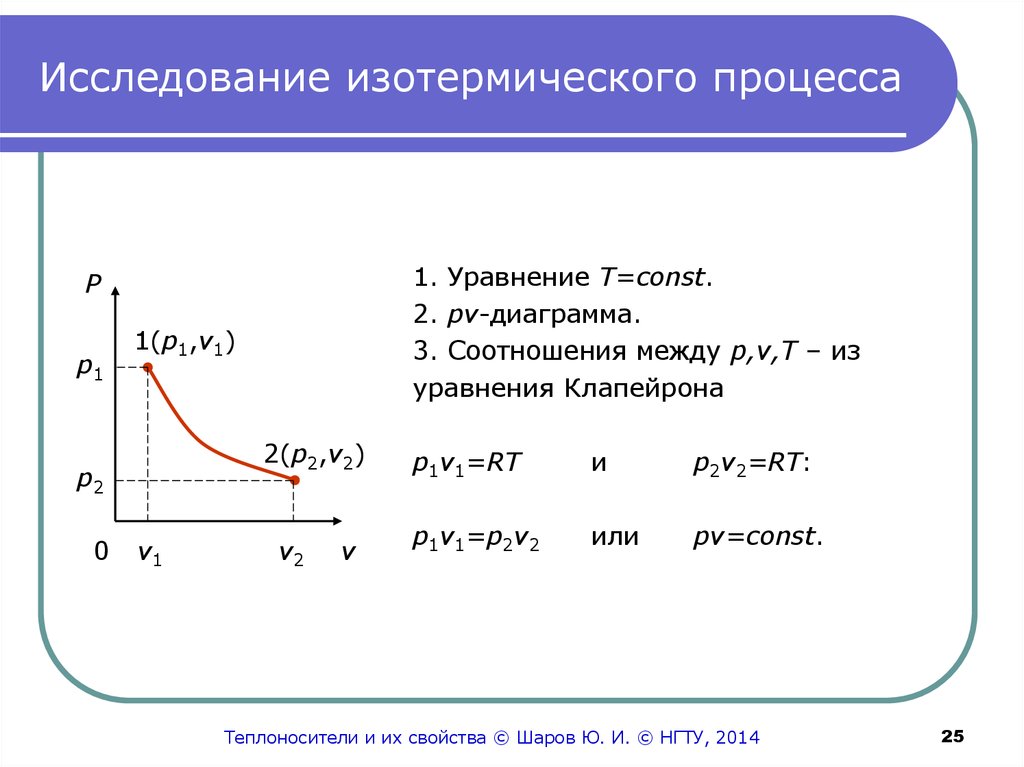
25. Исследование изотермического процесса
1. Уравнение T=сonst.2. pv-диаграмма.
3. Соотношения между p,v,T – из
уравнения Клапейрона
P
p1
1(p1,v1)
2(p2,v2)
p2
0
v1
v2
v
p1v1=RT
и
p2v2=RT:
p1v1=p2v2
или
pv=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
25
26. Исследование изотермического процесса
4. Изменение внутренней энергии:Δu=cvΔT=0.
Подстановка для работы pv=p1v1; p=p1v1/v.
5. Работа:
v2
l
pdv p1v1 v 1 (dv / v) p1v1ln(v2 / v1) RT ln( p1 / p2)
v2
.
v1
6. Теплота: из I закона термодинамики:
q=l=RTln(p1/p2).
7. Энергетический коэффициент: φ=Δu/q=0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
26
27. Исследование адиабатного процесса
Уравнение адиабаты выводится из I закона термодинамики:dq=0=du+pdv или cvdT+pdv=0.
Сделаем подстановку из уравнения Клапейрона:
pv=RT; T=pv/R; dT=(pdv+vdp)/R.
После подстановки имеем: cv(pdv+vdp)/R+pdv=0.
Умножим полученное выражение на R/cv:
pdv+vdp+Rpdv/cv=0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
27
28. Преобразования выражения I закона термодинамики
С учетом уравнения Майера R=cp-cv:pdv+vdp+(cp-cv)pdv/cv=0.
Или с учетом показателя адиабаты cp/cv=k:
pdv+vdp+(k-1)pdv=0.
После приведения подобных членов и сокращения имеем:
vdp+kpdv=0.
Разделим переменные, поделив уравнение на pv:
dp/p+kdv/v=0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
28
29. Уравнение адиабатного процесса
После приведения подобных членов и сокращения имеем:vdp+kpdv=0.
Разделим переменные, поделив уравнение на pv:
dp/p+kdv/v=0.
После интегрирования при k=сonst:
lnp+klnv=сonst
или
ln(pvk)=ln(сonst).
После потенцирования получаем уравнение адиабатного
процесса:
pvk=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
29
30. pv-диаграмма адиабатного процесса
Ppv = Const
pvk = Const
p1
p2
0
1(p1,v1)
v1 v2a v2T v
2. pv-диаграмма.
Легко доказать, что адиабата идет
круче изотермы.
При p1=idem, p2=idem:
v2T/v1=p1/p2; (v2a/v1)k=p1/p2;
v2a/v1=(p1/p2)1/k.
При k=1,67-1,29 для газов
(p1/p2)1/k<p1/p2, т.е. v2a<v2T .
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
30
31. Соотношения между параметрами
3. Соотношения между p и v из уравнения процесса:p1v1k=p2v2k: p2/p1=(v1/v2)k;
(p2/p1)1/k=v1/v2 .
(1)
(2)
Из уравнения Клапейрона
p1v1=RT1; p2v2=RT2;
или
(p2/p1)v2/v1=T2/T1 .
(3)
Подставляем (1) в (3): (v1/v2)k(v1/v2)-1=T2/T1,
получаем соотношение между v и T: T2/T1=(v1/v2)k-1 .
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
(4)
31
32. Внутренняя энергия и работа газа
Подставляем (2) в (3): (p2/p1)(p2/p1)-1/k=T2/T1,получаем соотношение между p и T: T2/T1=(p2/p1)(k-1)/k.
(5)
4. Изменение внутренней энергии: Δu=cvΔT.
5. Для работы нужна подстановка: p1v1k=pvk; p=v-kp1v1k.
Итак, работа газа с учетом p1v1k=p2v2k:
k
p
v
pdv p1v1k v dv 1 1 (v12 k v11 k )
1 k
v1
v1
v2
v2
k
.
1
1
k
1
k
k
1
k
( p1v1 v1 p2v2 v2 )
( p1v1 p2v2 )
k 1
k 1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
32
33. Теплота и работа
Окончательно работа газа, Дж/кг:l=(p1v1-p2v2)/(k-1); l=(T1-T2)R/(k-1).
6. Теплота по I закону термодинамики:
q= 0=Δu+l ,
то есть работа газа в адиабатном процессе совершается за
счет уменьшения его внутренней энергии:
l=-Δu.
7. Энергетический коэффициент:
φ=Δu/q=Δu/0=∞.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
33

























 physics
physics








