Similar presentations:
Теоретические основы теплотехники
1.
Южно-Российский государственный технический университет(Новочеркасский политехнический институт)
Тепловые электрические станции
(Введение в специальность)
Тема 4
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕПЛОТЕХНИКИ
«Повсюду, где имеется разность
температур, может происходить
возникновение движущей силы»
(Сади Карно)
Ефимов Николай Николаевич – проф., д.т.н., зав каф. ТЭСиТ
2. Что такое термодинамика
Термодинамика это наука, изучающая физическиесвойства макроскопических систем (тел и полей) на
основе анализа возможных в этих системах
превращений энергии без обращения к их
микроскопическому строению.
Основное содержание термодинамики – рассмотрение
общих свойств физических систем в состоянии
термодинамического равновесия, а также общих
закономерностей процессов изменения состояния.
Термодинамика вместе с тепломассообменом
является составной частью теоретических основ
теплотехники, которая в свою очередь является
фундаментальной базой всей теплоэнергетики.
3. Виды термодинамики
В инженерной практике различают:общую или физическую термодинамику;
химическую термодинамику, занимающуюся
приложениями законов термодинамики к химическим и
физико-химическим процессам (изучение тепловых
эффектов химических реакций, химического
равновесия, фазового равновесия и др.);
техническую термодинамику, занимающуюся
приложениями законов термодинамики в теплотехнике
(разработка теории теплосиловых установок,
двигателей и др.);
термодинамику необратимых процессов, в которой
изучаются необратимые процессы с помощью
термодинамических законов (например, определяются
их скорости в зависимости от внешних условий)
4. Термодинамическая система
Термодинамическая система это совокупность тел(субстанций), могущих обмениваться между собой и с
другими телами энергией и веществом.
Терм. системой является система, обладающая очень
большим числом степеней свободы.
Термодинамическая система может быть физически
однородной, если ее состав и все физические свойства
одинаковы в любых, произвольно выбранных частях.
Термодинамическая система является химически
однородной, если она состоит из одного химического
вещества.
Материальные тела термодинамической системы
разделяются на источники тепла и рабочие тела,
которые совершают механическую работу под
воздействием источников
5. Термодинамические процессы
Термодинамический процесс это всякое изменение,происходящее в термодинамической системе и связанное
с изменением хотя бы одного из ее параметров.
Существуют обратимые, необратимые и
квазистатические процессы.
Обратимый процесс это процесс перехода системы из
одного состояния в другое предполагающий возможный
обратный переход, последовательно повторяющий все
промежуточные состояния прямого процесса. Процесс
обратим, если он является квазистатическим процессом.
Квазистатический процесс это процесс, скорость
распространения которого в ограниченной системе столь
велика, что за время распространения процесса вдоль
всей системы ее состояние не успевает заметно
измениться.
6. Термодинамическое равновесие
Термодинамическое равновесие это состояние, вкоторое, в конце концов, приходит
термодинамическая система, находящаяся при
неизменных внешних условиях. При этом система
находится в состоянии механического равновесия, а
параметры состояния не изменяются с течением
времени, т.е. могут совершать малые колебания
около неизменных средних значений, что
называется флуктуацией.
Разновидностью термодинамического равновесия
является тепловое равновесие, при котором все
части системы имеют одну и ту же температуру.
7.
Химическое термодинамическоеравновесие
Химическое термодинамическое равновесие это
состояние реакционной системы, характеризующееся
тем, что химическая реакция идет одновременно в двух
противоположных направлениях с одинаковой
скоростью.
В результате состав системы (например, O2+N2=2NO)
остается постоянным, пока сохраняются условия ее
существования (температура, давление).
Каждая химическая реакция в состоянии равновесия
характеризуется соотношением между концентрациями
участвующих в ней веществ – константой равновесия.
Определяя положение равновесия для различных
температур и давлений, можно судить, какое их
сочетание наиболее благоприятно для практических
целей
8. Термодинамические параметры
Основными понятиями, которыми оперирует термодинамика,являются теплота и работа, которые являются различными
формами движения материи и проявления энергии.
Теплота (один из видов энергии) это результат
молекулярного и внутримолекулярного хаотического
движения частиц материи. Если теплоемкость постоянна,
то теплота определяется по уравнению
Q c m (T2 T1)
,
где т – масса тела, кг;
с – теплоемкость, Дж/(кг К);
Т1, Т2 –температуры, К.
Работа (вид механической энергии) – направленное
движение тел, происходящего под действием внешних сил.
Теплота и работа определяются значениями единицы
энергии 1 Дж = 0,278·10-6 кВт ч; 1 ккал = 4,19 кДж.
9. Термодинамические параметры (продолжение)
Температура - интенсивность теплового движения атомов,молекул и других частиц, образующих равновесную
термодинамическую систему. Абсолютная температура равна
Т в (т с 2 ) 2 ,
где т – масса, кг;
с –скорость поступательного движения молекул, м/с;
в – коэффициент пропорциональности.
Существуют две шкалы температур: Кельвина (абсолютная), К
и Цельсия (относительная) 0С; Т (0К) = t(0С) + 273.
Давление – сила, действующая по нормали на единицу
поверхности. давление может быть атмосферное рат,
абсолютное р, избыточное ризб. Размерность давления 1 Па = 1
н/м2 = 1 (кг·м)/(м2с2); 1 атм = 0,098 МПа. Абсолютное давление
окружающего воздуха называется барометрическим
давлением рбар. Избыточное давление является
относительным давлением: Ризб = р – рбар.
10. Термодинамические параметры (продолжение)
Плотность , кг/м3, - отношение массы к объему;В практике используется понятия удельный объем v, м3/кг и
удельного веса: γ = ρ·g= т·g/ V.
Плотность может характеризовать фазу вещества:
для газов = 0,2 ÷ 2,5 кг/м3; для жидкостей = 500 ÷ 3000
кг/м3; для твердых веществ > 1000 кг/м3.
Энтропия функция состояния термодинамической системы,
характеризующая направление протекания процесса теплообмена
между системой и внешней средой, S – Дж/(кг·К);
Энтальпия функция состояния термодинамической системы,
определяемая как сумма внутренней энергии системы и
произведения давления на объем системы. Удельная энтальпия h
имеет размерность Дж/кг.
Теплоемкость вещества это количество теплоты необходимое для
нагрева вещества на 10С. Удельная теплоемкость может быть
массовой, объемной и мольной, а также при постоянных
давлениях и объемах.
11.
Уравнения состояния газовСостояние идеальных газов описывается уравнением
Клапейрона:
8314
pv
T ,
p v R T или
где R – газовая постоянная, Дж/(кг К);
µ - молекулярная масса вещества.
В уравнение не учитываются силы сцепления между
молекулами; молекулы рассматриваются как материальные
точки приложения сил, создающих движение молекул;
молекулы совершают только поступательные движения.
Для реальных газов используется уравнение Ван-дерВаальса:
а
р v b RT
,
v2
где а коэффициент, учитывающий межмолекулярные
силы;
b собственный объем молекул.
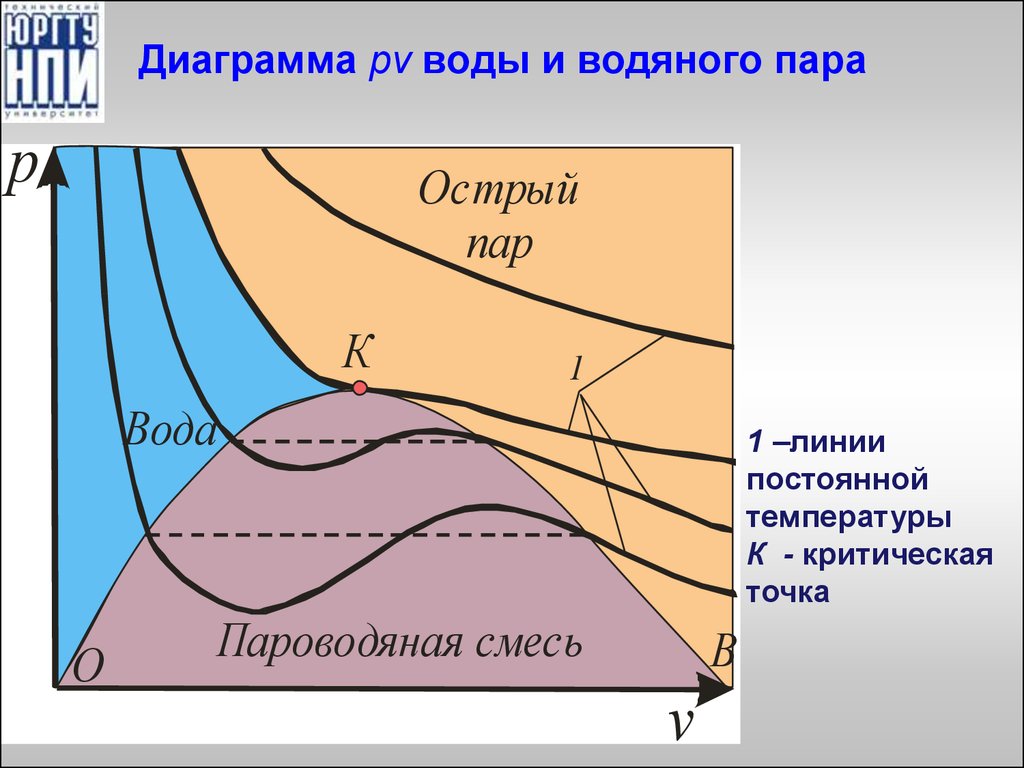
12. Состояние веществ
Любое вещество может находиться в газообразном,жидком и твердом состоянии.
Переход из одной фазы в другую связан с
изменениями параметров при подводе (отводе) тепла.
Процесс перехода воды из жидкого состояния в
газообразное называется парообразованием, а
обратный процесс конденсацией.
Параметры критической точки К:
давление - 22,115 МПа;
температура – 374,12 0С;
удельный объем – 0,003147 м3/кг;
удельная энтальпия – 2095,2 кДж/кг;
удельная энтропия – 4,4237 кДж/кг.
13. Диаграмма pv воды и водяного пара
рОстрый
пар
К
1
Вода
О
1 –линии
постоянной
температуры
К - критическая
точка
Пароводяная смесь
В
v
14. Основные законы идеальных газов
Закон Бойля-Мариота (открыт в 1662-1676 г.):p·v =const или p1v1 = p2v2 при T = const.
Закон Гей-Люссака выведенный им в 1882 г.:
v/T = const или v1/v2 = T1/T2 при p = const.
А Авогадро установил в 1811 г. - в равных объемах
разных идеальных газов при p = const и T = const
находится одинаковое количество молекул. Отсюда два
следствия:
Следствие 1. Массы газов в одинаковых объемах (V1 =
V2) при p = idem и T = idem относятся друг к другу как их
т
молекулярные массы: 1 1
2
т2
Следствие 2. Количество разных газов, находящихся
при одинаковых давлениях и температурах,
относящиеся между собой как молекулярные массы этих
газов, должны иметь одинаковый объем Vµ = idem/
15. Основные законы идеальных газов (продолжение)
Объем 1 киломоля при нормальных условияходинаков для любых идеальных газов и равен 22,4
м3/кмоль.
Нормальные физические условия: р=0,1014 МПа,
Т=273,15 0К.
Тогда в соответствии с уравнением Клапейрона:
p V μ 0,1014 10 6 22,4
Дж
Rμ
8314,33
T
273,15
кмоль К
Rµ = 8314,33 Дж/(кмоль К) – универсальная
газовая постоянная.
Газовая постоянная, R, Дж/(кг К), любого газа
определяется из соотношения
8314,33
R
μ
16. Первое начало термодинамики
1-е опредление. Энергия не исчезает и не возникает вновь,она лишь переходит из одного вида в другой.
Согласно первому началу термодинамики теплота Q,
сообщаемая системе, расходуется на изменение внутренней
энергии системы ΔU и совершение системой работы против
внешних сил :
dq du dl,
dQ dU dL или
2-е опредление Если тело совершает работу большую, чем
то количество теплоты, которое к нему подведено, то
внутренняя энергия убывает.
Если система находится в движении: в сечении 1-1 газ
обладал внутренней u1, потенциальной (p1v1) и кинетической
(с12/2 ) энергиями, а в сечении 2-2 соответственно и2, (p2v2) и
(с22/2), то по закону сохранения энергии
c12
c 22
u1 p1v1
u2 p2v 2
q
2
2
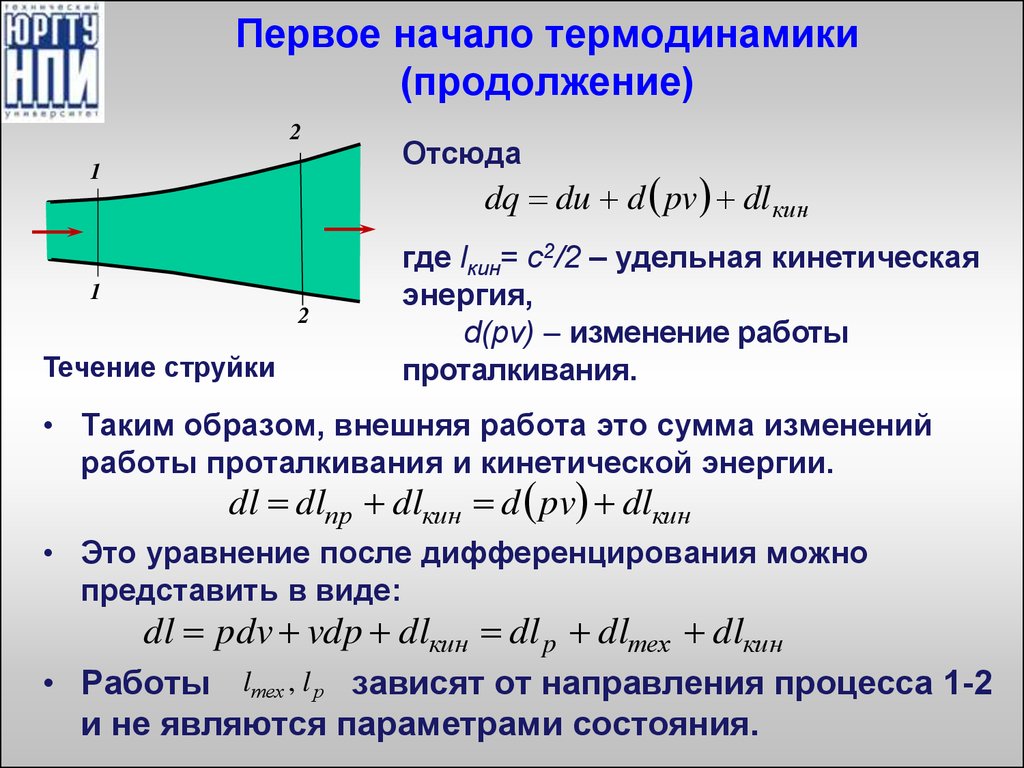
17. Первое начало термодинамики (продолжение)
2Отсюда
dq du d pv dl кин
1
1
2
Течение струйки
где lкин= с2/2 – удельная кинетическая
энергия,
d(pv) изменение работы
проталкивания.
• Таким образом, внешняя работа это сумма изменений
работы проталкивания и кинетической энергии.
dl dlпр dlкин d pv dlкин
• Это уравнение после дифференцирования можно
представить в виде:
dl pdv vdp dlкин dl p dlтех dlкин
• Работы lтех , l р зависят от направления процесса 1-2
и не являются параметрами состояния.
18. Свойства термодинамических процессов
• Равновесные и неравновесные процессы. Процесс, прикотором изменение какого-либо параметра происходит
одновременно во всех точках тела, называются
равновесными.
• Обратимые и необратимые процессы. Это такие процессы,
которые можно провести в обратном направлении, так что и
рабочее тело и окружающая среда пройдут через те же
точки и промежуточные состояния в той же
последовательности, что и прямом направлении.
• Различают внутренние и внешние обратимые процессы.
Внутренние обратимые процессы возможны, когда они
равновесны и нет обмена энергиями с окружающей средой.
• В реальных условиях изменение параметров
распространяется последовательно по точкам от места
возмущения, и поэтому такие процессы называются
неравновесными.
• Все реальные процессы неравновесные и необратимые
19. Свойства термодинамических процессов (продолжение)
• Термодинамические процессы могут бытьстационарными и нестационарными. Если процесс
изменяется во времени, то он называется
нестационарным или неустановившимся, и,
наоборот, если происходит изменение параметров
термодинамического процесса во времени, то он
называется стационарным или установившимся.
20. Термодинамические процессы идеальных газов
Уравнение состояния идеального газа pv =RT вдифференциальной форме имеет вид:
.
p dv v dp R dT
Это уравнение дает возможность определять один
параметр при двух других известных в любой точке
процесса.
Первый закон термодинамики
dq du pdv
устанавливает для любой точки процесса соотношение
между dq, du и pdv. При этом не оговаривается характер
термодинамического процесса.
Однако для определения q или работы lp необходимо
знать закономерность изменения любых двух
параметров состояния.
21. Термодинамические процессы идеальных газов (продолжение)
Закономерности изменения параметров могут бытьописаны следующими процессами:
изохорный (v = const);
изобарный (p = const);
изотермический (Т = const);
адиабатический (ds = 0; dq = 0);
политропный процесс (параметры изменяются)
Для каждого из этих процессов справедливы
следующие соотношения:
dq du pdv dh vdp;
pv RT .
22. Изохорный и изобарный процессы
1. Изохорный процесс: v = const.dv = 0; dq = du;
p1/T1 = p2/T2 - уравнение Шарля.
• Учитывая уравнения первого начала термодинамики получим:
dq du cv dT ;
Δq Δu cv T2 T1 .
2. Изобарный процесс: p = const.
v1/T1 = v2/T2 - уравнение Гей-Люссака.
l p v2 v1 R T2 T1 получим
При Δu cv T2 T1 ;
Δq cv T2 T1 R T2 T1 cv R T2 T1 .
Если принять, что c p c v R , то Δq c p T2 T1 .
R c p c v - уравнение Майера.
Если первый закон термодинамики выразить уравнением
dq dh vdp , то при p = const dq = dh и тогда ср(Т2 – Т1)= h2 – h1 .
23. Изотермический и адиабатический процессы
3. Изотермический процесс: Т = const.р1v1 p2 v2 - уравнение Бойля-Мариотта. du cv dT 0 ; dh c p dT 0
v2
p1
dq
dl
l
RT
ln
RT
ln
Тогда
или
v1
p2
.
4. Адиабатный процесс – это процесс без теплообмена: dq = 0.
Тогда из первого закона термодинамики получим:
du dl cv dT pdv 0 или dl du ; pdv cv dT
С другой стороны
cp cv
c p cv T
RT
или cv dT
p
Tdv 0
v
v
v
Последнее уравнение разделим на выражение сvТ и обозначим
отношение ср/сv через коэффициент адиабаты - k. Получим
k 1
dT
dv
T2
v2
k 1
0 . Отсюда ln
k 1 ln 0 или T2 v2 .
T
v
T1
v1
T1 v1
Используя уравнение Клапейрона, получим
k
p1v1
k
p 2 v2
p v const
k
.
24. Политропный процесс
5. Политропный процесс – общий процесс, объединяющий всевышеперечисленные.
dl dq du
du
cv
1
1
Обозначим
dq
dq
dq
c
,
где с – теплоемкость, которая, учитывая последнее обозначение,
определяется по уравнению
с с м 1 .
Следовательно, dq c dT , а p RT v T c p cv v
.
Тогда cdT cv dT c p cv T dv v или c cv dT T c p cv dv v .
После интегрирования последнее уравнение представляется в виде:
ln T2 T1 c p cv
c cv ln v2 v1
Проведем некоторые преобразования: c p cv 1 1 1 c c p 1 n
c cv
c cv
где п – показатель политропы.
Таким образом, можно придти к виду: T1v1n 1 T 2v 2n 1 T v n 1 ,
или
.
n
n
n
p1v1 p2v2 p v
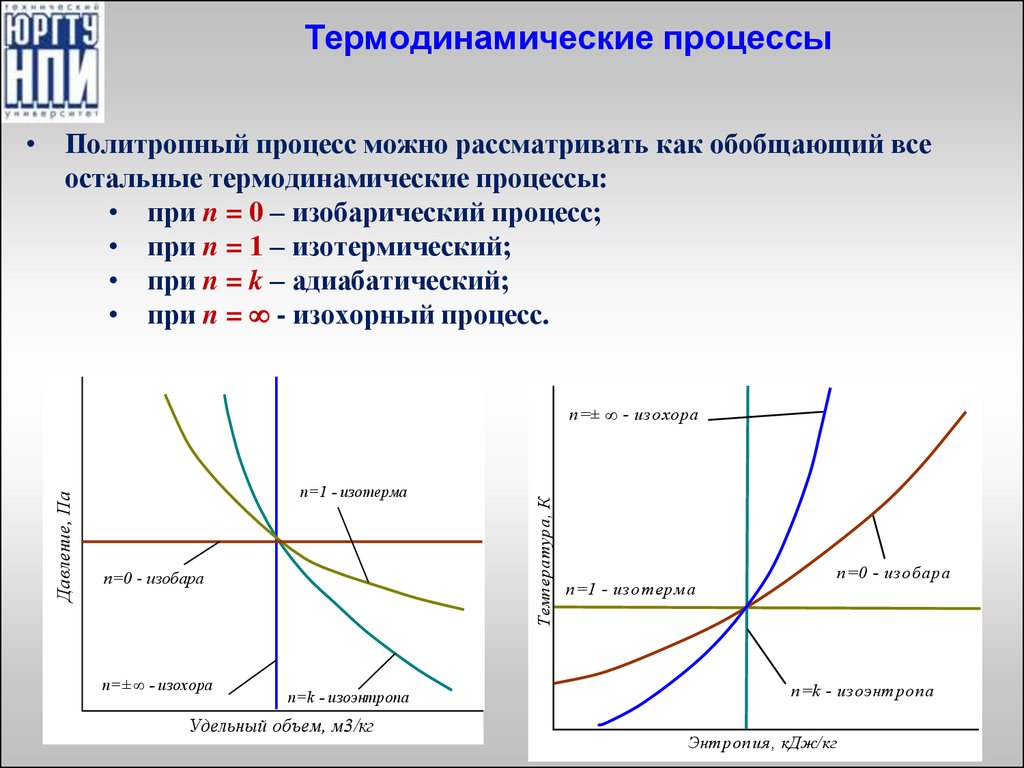
25. Термодинамические процессы
• Политропный процесс можно рассматривать как обобщающий всеостальные термодинамические процессы:
• при n = 0 – изобарический процесс;
• при n = 1 – изотермический;
• при n = k – адиабатический;
• при n = - изохорный процесс.
n=1 - изотерма
n=0 - изобара
n=± ∞ - изохора
n=k - изоэнтропа
Удельный объем, м3/кг
Температура, К
Давление, Па
n=± ∞ - изохора
n=1 - изотерма
n=0 - изобара
n=k - изоэнтропа
Энтропия, кДж/кг
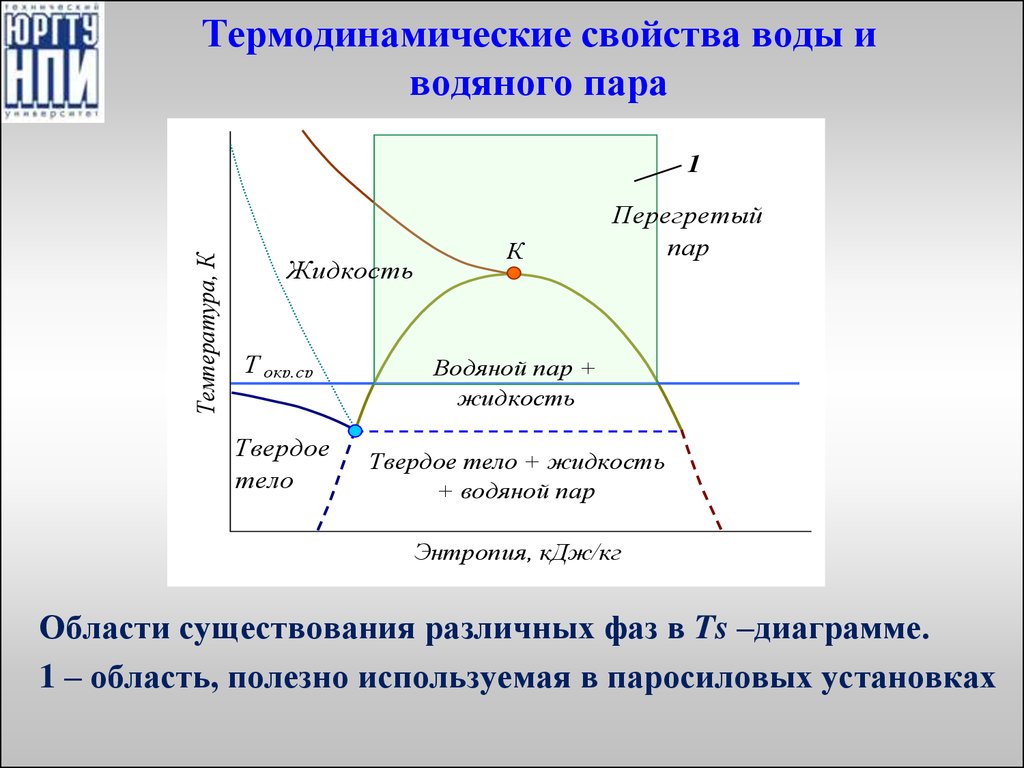
26. Термодинамические свойства воды и водяного пара
Температура, К1
Жидкость
Т окр.ср
Твердое
тело
К
Перегретый
пар
Водяной пар +
жидкость
Твердое тело + жидкость
+ водяной пар
Энтропия, кДж/кг
Области существования различных фаз в Ts –диаграмме.
1 – область, полезно используемая в паросиловых установках
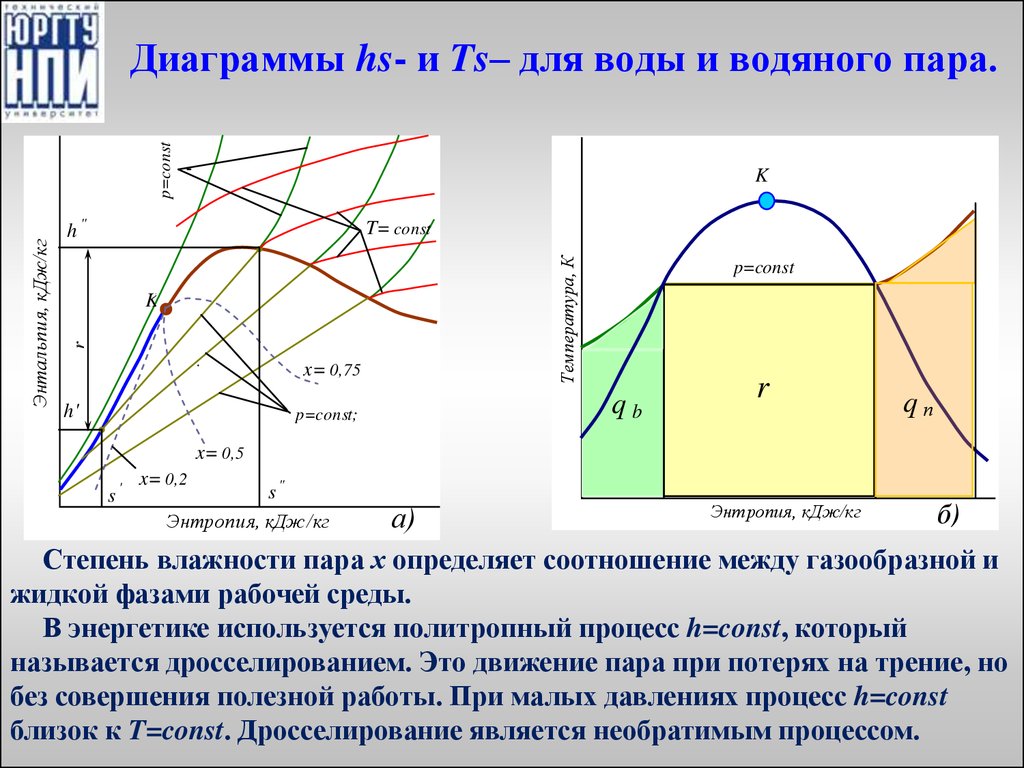
27. Диаграммы hs- и Ts– для воды и водяного пара.
Kh ''
K
x= 0,75
h'
x= 0,5
s'
p=const;
T=const
Температура, К
T= const
r
Энтальпия, кДж/кг
p=const
Диаграммы hs- и Ts– для воды и водяного пара.
p=const
qb
r
qп
x= 0,2
s"
Энтропия, кДж/кг
Энтропия, кДж/кг
б)
а)
Степень влажности пара х определяет соотношение между газообразной и
жидкой фазами рабочей среды.
В энергетике используется политропный процесс h=const, который
называется дросселированием. Это движение пара при потерях на трение, но
без совершения полезной работы. При малых давлениях процесс h=const
близок к T=const. Дросселирование является необратимым процессом.
28. Термодинамические циклы
Цикл (круг, от греч.) совокупность процессов в системепериодически повторяющихся явлений, при которых
объект, подвергающийся изменению в определенной
последовательности, вновь приходит в исходное
положение.
Непрерывность действия тепловой
машины обеспечивается тем, что
рабочее тело с параметрами p, V, T ,
пройдя последовательно ряд
состояний процесса расширения на
пути 1а2, а затем ряд состояний
сжатия 2б1 вновь возвращается в
исходную точку и цикл может быть
повторен.
р
а
р1
1
2
р2
б
v1
v2
v
29. Работа цикла
При процессе расширения работа (тепло) подводится крабочему телу и тогда:
q ðàñø l ðàñø Δu ðàñø qïîäâ
Для осуществления процесса сжатия тепло отводится:
qñæ lñæ Δuñæ qîòâ
Так как внутренняя энергия является функцией
состояния, т.е. величиной не зависящей от пути процесса, то
для любого кругового Δu
цикла:
ðàñø Δuñæ
Следовательно qïîäâ qîòâ l ðàñø lñæ lö
Таким образом, полезная работа равна разности количеств
тепла, подведенного и отведенного при совершении цикла.
30. Второй закон термодинамики
Для осуществления термодинамического цикла необходимоиметь не только источник тепла (теплоотдатчик) qподв , но и
холодильник (теплоприемник) qотв , без которого невозможен
возврат рабочего тела в исходную точку. Это условие и
составляет содержание второго начала термодинамики.
В то время как первый закон термодинамики характеризует
процессы превращения энергии с количественной стороны,
второй закон определяет качественную сторону этих
процессов.
Теплота горячего источника в круговом процессе (цикле) не может быть
полностью превращена в работу, так как часть подведенного тепла должна
быть передана более холодному источнику (холодильнику
Второй закон термодинамики обычно записывается
уравнением
T ds dQ
31. Термодинамические циклы
Если процессы расширения располагаются вышепроцессов сжатия ( l ðàñø lñæ ), то такие циклы называются
прямыми. Для них работа цикла – положительная величина.
Прямые циклы осуществляются в теплоэнергетических
установках. Если же процессы располагаются наоборот обратные циклы. Здесь работа цикла – величина
отрицательная. В таких циклах работа подводится извне и в
результате совершения цикла превращается в тепло, т.е.
здесь осуществляется перенос тепла от холодного источника
к горячему. Такой цикл используется в холодильных
установках и тепловых насосах.
Оценкой совершенства прямых циклов является
термический коэффициент полезного действия
t
lö
q1
q1 q2
q
1 2
q1
q1
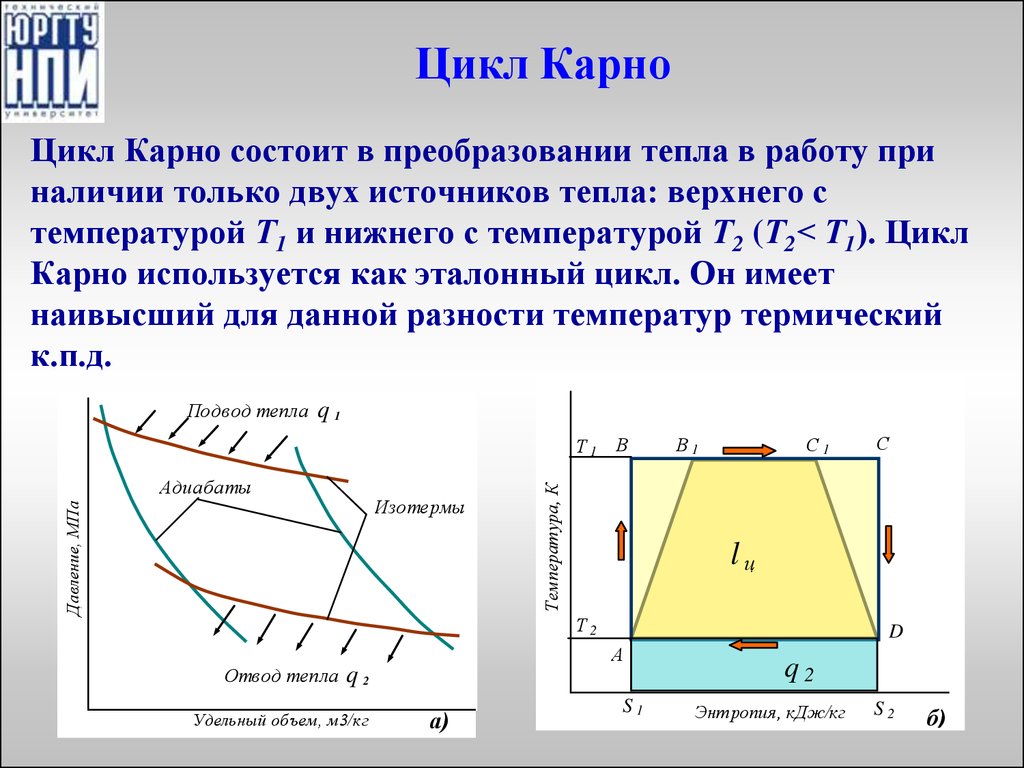
32. Цикл Карно
Цикл Карно состоит в преобразовании тепла в работу приналичии только двух источников тепла: верхнего с
температурой Т1 и нижнего с температурой Т2 (Т2< Т1). Цикл
Карно используется как эталонный цикл. Он имеет
наивысший для данной разности температур термический
к.п.д.
Подвод тепла
q1
Адиабаты
Давление, МПа
Изотермы
Температура, К
Т1 В
В1
С1
lц
Т2
Отвод тепла
D
А
q2
Удельный объем, м3/кг
а)
С
S1
q2
Энтропия, кДж/кг
S2
б)
33. Цикл Ренкина
На всех ТЭС и АЭС активно используется цикл, открытыйшотландским инженером-физиком У. Ренкином в Х1Х веке.
h
l
4
1
5
2
6
e
K
Температура, К
3
k
c
g
b
d
b1
7
a
а)
я
Энтропия, кДж/кг
f
f1
б)
Обратимый докритический цикл Ренкина описывается в Тs –диаграмме
процессами abcdefa, необратимый цикл – ab1cdef1a, где процессы аb
осуществляются в насосах (7, а); bcde – в котле (1, последовательно в
водяном экономайзере, испарительных поверхностях нагрева и
пароперегревателе); ef – в паровой турбине (3, 4); fa – в конденсаторе (6)
34. Общие понятия о процессе теплообмена
Теплообменом называется необратимыйсамопроизвольный процесс переноса тепловой энергии в
пространстве с неоднородным полем температуры.
Существуют три основных способа передачи тепловой
энергии:
– теплопроводность;
– конвективный теплообмен;
– теплообмен излучением.
Теплопроводность –обмен энергией при соприкосновении отдельных
частиц тела, имеющих различную температуру (в твердых телах).
Конвекция – теплообмен в реальных жидкостях или газах в форме
переноса тепла при перемещении частиц или объемов веществ из одной
области в другую.
Излучение – теплообмен путем распространения лучистой энергии, т.е.
электромагнитных волн определенной длины.
35. Теплопроводность
Теплопроводность –теплообмен, при котором перенос тепловой энергии внеравномерно нагретой среде имеет атомно-молекулярный характер.
В газах перенос энергии осуществляется хаотически движущимися
молекулами, в металлах – в основном электронами проводимости, в
диэлектриках – за счет связанных колебаний частиц, образующих
кристаллическую решетку.
Закон Фурье, согласно которому вектор плотности теплового потока
dt
q λ
λ grad t
dn
λ – коэффициент теплопроводности, Вт/(м·К)
t
t2
λ для: стали - 63 Вт/(м·К); вода – 0,53 Вт/(м·К);
воздух (газ) – 0,025 Вт/(м·К)
Для многослойных стенок тепловой поток
ti
t1 t n
q λ n
si
λ
i 1 i
Температура, К
1
tn
s
si
sn
Ширина стенки, м
36. Конвективный теплообмен
Конвективный теплообмен – процесс переноса теплоты в неравномернонагретой жидкой, газообразной или сыпучей среде, осуществляющийся
вследствие движения среды и ее теплопроводности. Различают:
• конвективный теплообмен при естественной (свободной) конвекции,
когда движение среды обусловлено только действием силы тяжести на
неравномерно нагретую среду;
• конвективный теплообмен при вынужденной конвекции, когда
движение среды вызывается действием на нее механизмов.
Тепловой поток при конвективном теплообмене определяется
уравнением Ньютона: q tñò t æ
α – коэффициент теплоотдачи, Вт/(м2К)
Движущаяся среда
Коэффициент
теплоотдачи
Вода
Вязкие жидкие среды
Газы
Характер движения
Свободное (ламинарное)
Принудительное
(турбулентное)
100 ÷ 600
50 ÷ 10000
-
50 ÷ 500
3 ÷ 20
10 ÷100
37. Теплопередача через стенку
,Этапы теплопередачи через стенку
1. Теплопередача от более горячей движущейся среды к поверхности стенки,
осуществляемая конвективным теплообменом: q α1 t1 t1c ;
2. Теплопроводность через твердую стенку:
q
λ
t1c t 2c ;
s
Температура, К
3. Теплопередача от поверхности стенки
q α2 t 2c t 2 .
к более холодной движущейся среде.
Суммарная теплопередача через стенку:
t1 t 2
q
t1
q
k t1 t 2
1 s 1
α1 λ α 2
t 1c
• ,
t 2c
t2
Стенка
Среда 1
s
Линейный размер, м
Среда 2
Полное количество теплоты, передаваемого
через стенку в единицу времени:
Q q F kF t1 t 2 kF Δt
Δt
- температурный напор
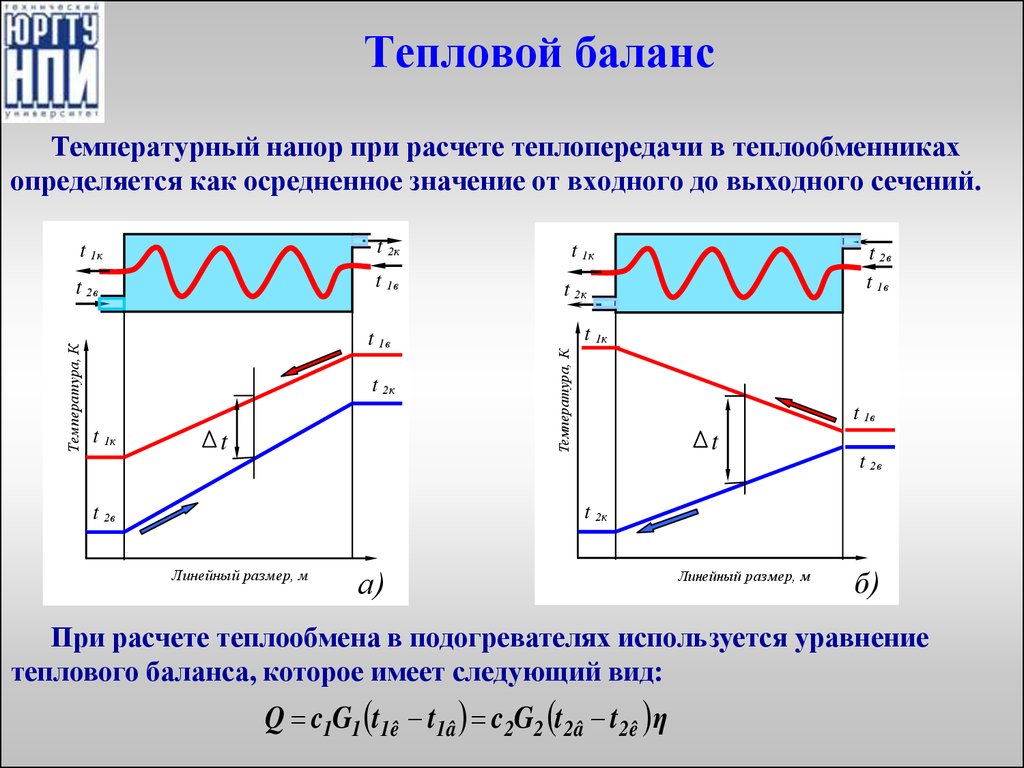
38. Тепловой баланс
Температурный напор при расчете теплопередачи в теплообменникахопределяется как осредненное значение от входного до выходного сечений.
t 2в
t 1в
t 1в
t 2к
t 1к
t
t 1к
t 2в
t 1в
t 2к
t 1к
Температура, К
t 2к
Температура, К
t 1к
t 1в
t
t 2в
t 2к
t 2в
Линейный размер, м
а)
Линейный размер, м
б)
При расчете теплообмена в подогревателях используется уравнение
теплового баланса, которое имеет следующий вид:
Q c1G1 t1ê t1â c2G2 t 2â t 2ê η
39. Теплообмен излучением
Электромагнитное излучение с длиной волны от 8·10-10 до 8·10-4 м создаеттепловое воздействие. Такой теплообмен возникает за счет хаотического
движения молекул одного тела, которое передается другому телу, вызывая в
нем аналогичные колебания молекул
Для практических расчетов процесса лучистого
1
2
теплообмена используется теория СтефанаЕ
Больцмана (1884 г.), согласно которой энергия
излучения абсолютно черного тела равна
Е0
4
АЕ 0
Ò
E0 σ0 T Ñ0
100
4
Для любого серого тела:
Ò
4
E ε Å0 ε σ 0 Ò Ñ
100
С0 = 5,67, Вт/( м2К4) – коэффициент излучения
4
(1-А)Е 0
2
1
Рис.3.14. Лучистый теплообмен между
между телами 1 и 2
абсолютно черного тела
ε = С/С0 – степень черноты тела
2
4
С = 0÷5,67 Вт/( м К ) - коэффициент излучения серого тела
Полная тепловая энергия,
T 4 T 4
полученная телом при
Q1 2 q1 2 F C ïð F 1 1
100 100
лучистом теплообмене
40. Южно-Российский государственный технический университет (Новочеркасский политехнический институт)
Благодарю за вниманиеЕфимов Николай Николаевич – проф., д.т.н., зав
каф. ТЭС

































 physics
physics








