Уравнения состояния термодинамических систем. Лекция № 12

1. Лекция № 12

УРАВНЕНИЯ СОСТОЯНИЯ
ТЕРМОДИНАМИЧЕСКИХ
СИСТЕМ
Лекции Веретимус Н.К. и Веретимус Д.К.

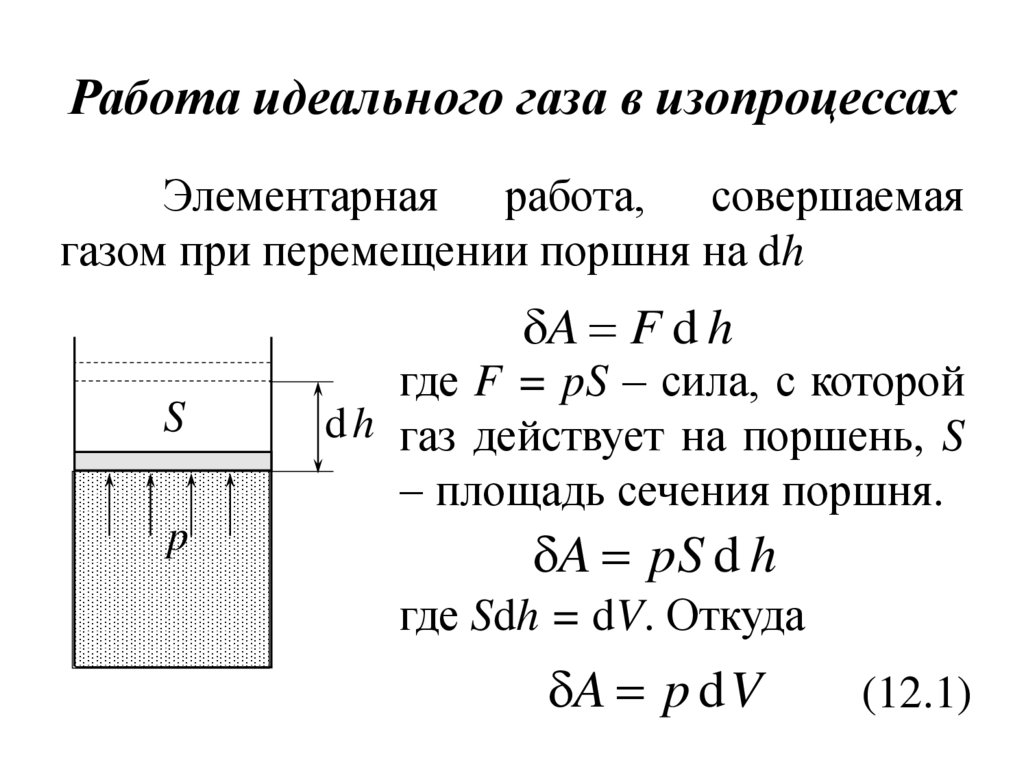
2. Работа идеального газа в изопроцессах

Элементарная работа, совершаемая
газом при перемещении поршня на dh
A F d h
S
где F = pS – сила, с которой
d h газ действует на поршень, S
площадь сечения поршня.
p
A pS d h
где Sdh = dV. Откуда
A p d V
(12.1)

3.

Работа,
совершаемая
газом
увеличении объема от V1 до V2:
A
при
V2
p dV
(12.2)
V1
Формула (12.2) справедлива для любых
изменений объема газа.
Работа
газа
в
изотермическом
процессе. Из уравнения процесса
pV RT const
выразим давление

4.

T
p R
V
Из (12.2) при const, T const
V2
V2
dV
T
A R dV RT
V
V
V
1
V1
Тогда
работа
идеального
изотермическом процессе
V2
A RT ln
V1
газа
в
(12.3)

5.

Работа газа в изобарическом процессе
при const, p const. Из (12.2)
V2
A p d V p V2 V1
(12.4)
V1
Работа газа в изохорическом процессе
при const, V const. Из (12.2)
A 0
(12.5)

6. Теплоемкость идеального газа при изопроцессах. Теплоемкость идеального газа.

1. Теплоемкость
тела
–
количество
теплоты, необходимое для нагрева
данного тела на один градус
Q
CT
dT
(12.6)
В СИ [CT] = Дж/К. Теплоемкость зависит от
процесса (т.к. зависит от δQ).

7.

2. Удельная теплоемкость вещества –
количество теплоты, необходимое для
нагревания единицы массы данного
вещества на один градус
СT 1 Q
c
,
m m dT
где m - масса тела. В СИ [c] = Дж/(кг К).
3. Молярная теплоемкость – количество
теплоты, необходимое для нагревания
одного моля данного вещества на один
градус

8.

Q 1 Q СT
C
,
m dT dT
где μ – молярная масса вещества, ν =m/μ –
количество вещества в теле. Размерность в
СИ [C] = Дж/(моль·К).
Удельная и молярная
связаны между собой:
теплоемкости
c С
Теплоемкость 1 моля идеального газа
при изобарическом процессе
с учетом
(10.1)
и
(10.2)
(I-ого
начала
термодинамики), (12.4) и (11.13)

9.

Q d U A i
dV
p const : C p
R p
dT dT dT 2
dT
Из (10.1) для ν = 1, p = const
тогда
p dV R d T
i 2
i
R
Cp R R
2
2
(12.7)
Теплоемкость 1 моля идеального газа
при изохорическом процессе CV
Q d U i
R
V const : CV
dT dT 2
(12.8)
Уравнение Майера
C p CV R
(12.9)

10. Адиабатический процесс, уравнение Пуассона

Адиабатический
(адиабатный)
процесс – процесс, который происходит без
теплообмена с окружающей средой (ν= const,
δQ = 0).
Запишем I-ое начало термодинамики
(10.2) для одного моля идеального газа (ν = 1
моль) при адиабатном процессе
i
0 dU A R d T p dV
2

11.

Из ур-я состояния идеального газа при ν = 1
d pV R d T
i 1
0 R p dV V d p p dV
2 R
i
i
1 p dV V d p
2
2
0
i
2 1
p dV V d p
i2
Учтем (12.7), (12.8). Обозначим

12.

i 2 Cp
CV
i
тогда
dV d p
0 p dV V d p
V
p
ln c ln V ln p,
(12.10)
где с – постоянная интегрирования. Откуда
уравнение адиабаты в переменных p, V или
уравнение Пуассона
pV const,
(12.11)
где γ – показатель адиабаты (см. (12.10)).

13.

Отметим, что адиабата идет круче
изотермы (pV = const ), т.к. γ > 1.
p
адиабата
изотерма
С учетом (11.1)
представим (12.11) в
переменных T, V
TV
1
const
(12.12)
V
Работа идеального газа в адиабатном
процессе
A dU CV d T
A12 CV T1 T2

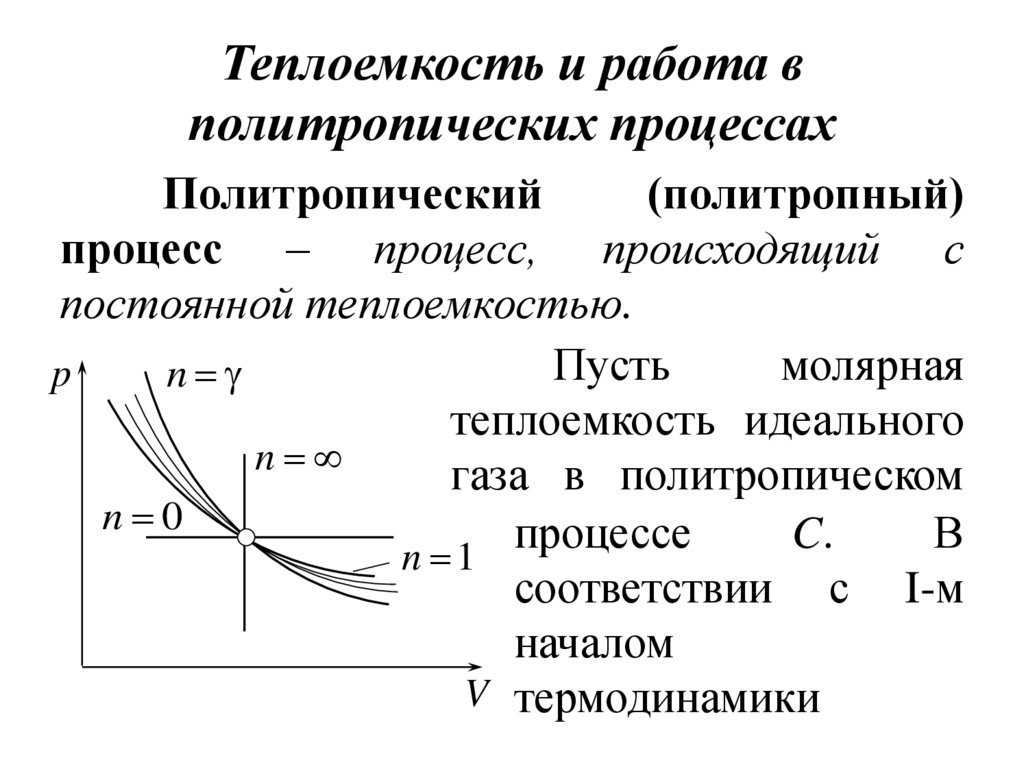
14. Теплоемкость и работа в политропических процессах

Политропический
(политропный)
процесс – процесс, происходящий с
постоянной теплоемкостью.
Пусть
молярная
p
n
теплоемкость идеального
n
газа в политропическом
n 0
процессе
C.
В
n 1
соответствии с I-м
началом
V термодинамики

15.

m
m
C d T CV d T p d V
m
p d V C CV d T
(12.13)
Подставляя (12.13) в выражение для
полного дифференциала от уравнения
Клапейрона-Менделеева:
m
p dV V d p R d T

16.

получаем
m
m
V d p R d T C CV d T
или с учетом уравнения Майера (12.9)
m
V d p C p C d T
(12.14)
При C CV, на основании формул (12.13) и
(12.14) получаем уравнение
np d V V d p 0
(12.15)

17.

Показатель политропы
n
C Cp
C CV
(12.16)
→ зависимость молярной теплоемкости C
от показателя политропы n
C
nCV C p
n 1
(12.17)
Преобразовав (12.15) к виду
dV d p
n
0
V
p

18.

после интегрирования получим уравнение
политропического
процесса
или
политропы
(12.18)
pV n const
Уравнение политропы можно записать в
термодинамических координатах T,V
n 1
(12.19)
TV
const
n – показатель политропы, произвольное
число. При соответствующих n уравнение
политропы описывает все изопроцессы: при
n = 1 – изотермический; при n = 0 –
изобарический, при n = – изохорический;
при n = γ – адиабатный процессы.

19.

Из (12.17) молярная теплоемкость
изотермического процесса C (n = 1).
Работу
газа
в
политропическом
процессе определим, подставив (12.18) в
(12.2), с учетом того, что
n
p1V1
n
n
p n
pV p1V1 const
V
Тогда
V2
V2
n dV
(12.20)
A p dV p1V1 n
V1 V
V1

20.

A
p1V1n
V2
p1V1n
dV
V n n 1 V
V1
n 1 V2
V1
p1V1n 1
1
n 1 n 1
1 n V2 V1
Работа газа в политропическом процессе
n 1
V1
p1V1
1 ,
A12
n 1 V2
(12.21)
где p1, V1 – начальные давление и объем газа;
V2 – конечный объем газа.
Из (12.21) следует, что работа при
расширении газа всегда положительна,
независимо от того, больше или меньше
единицы показатель политропы.

21.

Формула (12.21) неприменима для описания
изохорического (C ≠ CV) и изотермического
(C ) процессов.
Политроп.
процесс
Изотермический
Изобарный
1
A RT ln V2 V1
0
Cp
A p V2 V1
Изохорный
CV
0
Адиабатный
γ
0
1
V1
p1V1
1
A
1 V2
n
ТеплоемФ-ла для
кость
вычислен. работы

22. Газ Ван-дер-Ваальса

И. Ван-дер-Ваальс предложил уравнение
состояния реального газа, учитывающее
конечность объема молекул и наличие
межмолекулярных сил притяжения
a 2
p 2 V b RT
(12.22)
V
p, V, T – давление, объем и абсолютная
температура газа соответственно; a, b –
постоянные коэффициенты, характеризующие
взаимодействие
молекул
данного
газа
(определяют экспериментально); ν – кол-во
вещества, R 8,314 Дж моль К

23.

a
Для одного моля газа член 2
V
имеет размерность давления и учитывает
притяжение
молекул
в
результате
межмолекулярного
взаимодействия.
Константа b – поправка на собственный
объем молекул, учитывающая отталкивание
молекул на близких расстояниях.
На молекулы газа действуют силы
притяжения
и
отталкивания.
Они
действуют на небольших расстояниях, но
силы притяжения убывают медленнее сил
отталкивания.

24.

Силы притяжения внутри газа в среднем
скомпенсированы для каждой отдельной
молекулы. На расположенные в тонком слое
вблизи стенки сосуда молекулы действуют
силы притяжения со стороны других молекул,
направленные внутрь газа. Эти силы создают
дополнительное
давление,
которое
называется внутренним.
Суммарная сила, действующая на
элемент поверхностного слоя газа, должна
быть пропорциональна числу молекул газа в
этом элементе, а также числу молекул в слое
газа, непосредственно примыкающем к
рассматриваемому элементу.

25.

Толщина этих слоев определяется
радиусом действия сил притяжения и имеет
тот же порядок величины. При увеличении
концентрации молекул газа в l раз сила
притяжения, приходящаяся на единицу
площади поверхностного слоя, возрастет в l2
раз.
Поэтому величина внутреннего давления
растет
пропорционально
квадрату
концентрации n2 молекул газа.

26.

Тогда суммарное давление внутри газа
p p
a0 N
V
2
2
N
n
V
Здесь p – давление газа на стенку сосуда, a0 –
постоянная,
определяемая
физикохимическими свойствами молекул газа, N –
число молекул газа в объеме V, n –
концентрация молекул газа, p´ – давление,
которое создал бы идеальный газ при тех же
условиях.

27.

Обозначим
Тогда
a
2
a0 N A
a
p p 2
V
2
(12.23)
Поправка, связанная с действием сил
отталкивания. Учитываем только парные
взаимодействия между молекулами, поэтому
эти силы, в отличие от сил притяжения, не
будут зависеть от концентрации молекул. По
этой же причине силы отталкивания
проявляются во всем объеме газа, а не только
в поверхностном слое.

28.

Зависимость сил отталкивания от
расстояния между молекулами определяет
эффективное
сечение
взаимодействия
молекул, т.е. их размеры.
Для учета короткодействующих сил
отталкивания
необходима
поправка,
учитывающая
занимаемый
молекулами
объем. Ее значение пропорционально общему
числу молекул и зависит от их физикохимических свойств. Тогда свободный от
молекул объем:
V V b0 N
(12.24)

29.

Здесь b0 – коэффициент, определяемый
физико-химическими свойствами молекул
газа. Обозначив b b0 N A , получим
V V b
(12.25)
При больших V, а также для
разреженных газов, константами a и b можно
пренебречь, и уравнение Ван-дер-Ваальса
переходит
в
уравнение
КлапейронаМенделеева (уравнение состояния идеального
газа).

30.

Уравнение Ван-дер-Ваальса является
приближенным и количественно определяет
свойства реальных газов лишь в области
высоких температур и низких давлений.
Однако
качественно
оно
позволяет
описывать поведение газа при высоких
давлениях, конденсацию газа и критическое
состояние.

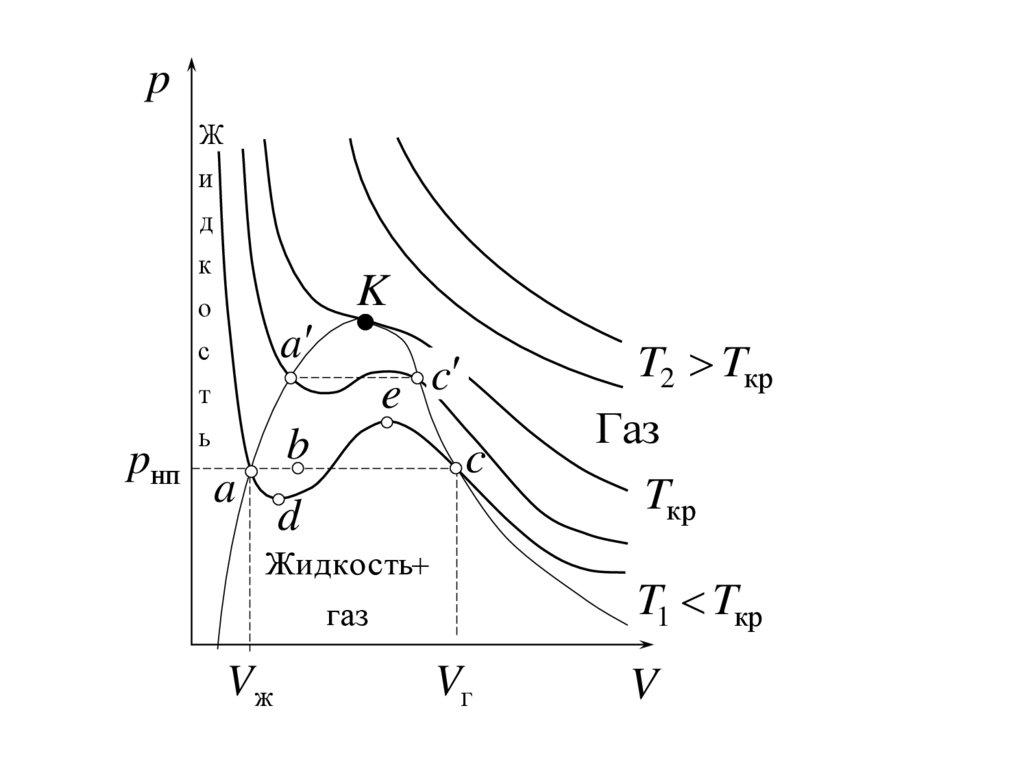
31.

p
Ж
и
д
к
о
a
с
K
e c
т
pнп
ь
b
a
c
d
Жидкость
T1 Tкр
газ
Vж
T2 Tкр
Газ
Tкр
Vг
V

32.

При T>Tкр вещество может находиться
только в одном (газообразном) состоянии, а
при T<Tкр - в трех состояниях (двух
стабильных – жидком Vж и газообразном Vг и одном нестабильном).
Точки прямой ac отвечают равновесию
жидкости и ее насыщенного пара. В условиях
равновесия, например, в т. b, относительное
количество жидкости и пара определяются
отношением отрезков bc/ba («правило
моментов») .

33.

Равновесию
фаз
при
определенной
температуре T соответствует давление
насыщенного пара pнп и интервал объемов от
Vж до Vг. При более низких p (за областью, где
возможно одновременное существование газа
и жидкости) изотерма характеризует свойства
газа.
Левая, почти вертикальная часть
изотермы отражает малую сжимаемость
жидкости. Участки ad и ec (и аналогичные
участки
других
изотерм)
относятся
соответственно к перегретой жидкости и

34.

переохлажденному пару (метастабильные
состояния). Участок
de физически
неосуществим, так как здесь происходит
увеличение объема V при увеличении
давления p.
Совокупность точек a, a , a и c, c , c
определяет кривую, называемую бинодалью,
которая очерчивает область совместного
существования
газа
и
жидкости.
В
критической точке K параметры TK, pK и VK
имеют значения, характерные для данного
вещества.

35.

При
температурах,
больших
TK,
изотермы
уравнения
Ван-дер-Ваальса
приближаются к изотермам идеального газа.
p
Реальная
изотерма, полученная
Эндрюсом
при
исследовании
углекислого
газа,
приводится на рис.
c
a
V

36. Внутренняя энергия газа Ван-дер-Ваальса

Пусть газ Ван-дер-Ваальса участвует в
адиабатическом процессе. Тогда
d U A pdV
(12.26)
При тех же условиях изменение
внутренней энергии идеального газа:
d U p d V

37.

Подставим в эту формулу соотношения
(12.23) и (12.25)
a 2
d U p 2 d V b
V
2
(12.27)
a
p dV 2 dV
V
Первое слагаемое в правой части (12.27),
согласно
(12.26),
представляет
собой
изменение внутренней энергии газа Ван-дерВаальса. Отсюда следует

38.

a 2
dU dU 2 dV
V
После интегрирования
2
a
U U
const
V
a 0 U U
С учетом
m
U CV T
Выражения для внутренней энергии
газа Ван-дер-Ваальса

39.

a
U CV T
V
2
(12.28)
Внутренняя энергия газа Ван-дерВаальса зависит не только от его
температуры, как в случае с идеальным газом,
но и от занимаемого им объема. В связи с
этим в изотермическом процессе будет
изменяться внутренняя энергия газа Ван-дерВаальса, а, следовательно, подведенная к газу
теплота не будет равна совершенной им
работе.

40. Литература:

•Глаголев К.В., Морозов А.Н. Физическая
термодинамика: Учеб. пособие. – М.: Изд-во
МГТУ им. Н.Э.Баумана, 2004. – 368 с./Под
ред. Л.К.Мартинсона, А.Н.Морозова.
•Иродов И.Е. Физика макросистем. Основные
законы. – М.: Лаборатория Базовых Знаний,
2001