Similar presentations:
Теплоемкость идеального газа при изопроцессах. Лекция 12
1. Лекция 12. Теплоемкость идеального газа при изопроцессах
Адиабатический процесс,уравнение Пуассона.
Политропический процесс.
Теплоемкость и работа в политропических
процессах.
Газ Ван-дер-Ваальса.
Внутренняя энергия газа Ван-дер-Ваальса.
2.
Мудрые люди обдумывают свои мысли,глупые провозглашают их.
Г. Гейне
Учение без размышления бесполезно,
размышление без учения опасно.
Конфуций
3. Теплоёмкость идеального газа при изопроцесах
Теплоёмкость тела характеризуетсяколичеством теплоты, необходимой для
нагревания этого тела на один градус
dQ
C
.
dT
Единица измерения теплоемкости: [C] = Дж/К.
Теплоёмкость – величина неопределённая,
поэтому используют понятия удельной и
молярной теплоёмкости.
2020 г. Чуев А.С.
3
4. Удельная теплоёмкость Суд или с – есть количество теплоты, необходимое для нагревания 1кг вещества на 1 градус:
C удdQ
c
m dT
[Cуд] = Дж/(кг К).
Для газов удобно пользоваться молярной
теплоемкостью Сμ количество теплоты,
необходимое для нагревания 1 моля газа на 1
градус:
dQ
Cμ
ν dT
Cμ Cуд μ
[C ] = Дж/(моль К).
μ
2020 г. Чуев А.С.
4
5. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней
1. Изохорныйпроцесс
Если газ нагревать при
постоянном объёме, то всё
подводимое тепло идёт на
нагревание газа, то есть
изменение его внутренней
энергии.
Теплоёмкость при
постоянном объёме СV
2020 г. Чуев А.С.
5
6. В общем случае так как U может зависеть не только от температуры. В случае идеального газа справедлива формула Из чего следует
UCV
T V
В общем случае
так как U может зависеть не только от
температуры.
В случае идеального газа справедлива
формула
dU C dT
V
T
Из чего следует U CV dT CVT
или
U CVT
0
2020 г. Чуев А.С.
i
CV 6 R
2
7. СР – теплоемкость при постоянном давлении Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень
2. Изобарныйпроцесс
Проводимое тепло
затрачивается и на
нагревание и на
совершение работы
C P CV .
СР – теплоемкость при постоянном давлении
Если нагревать газ при постоянном давлении Р в
сосуде с поршнем, то поршень поднимется на
некоторую высоту h, то есть газ совершит работу.
2020 г. Чуев А.С.
7
8. Пусть мы нагреваем один моль идеального газа при постоянном объёме. Из первого начала термодинамики: т.е. бесконечно малое
Связь между CP и CVCP CV R.
Пусть мы нагреваем один моль идеального газа при
постоянном объёме. Из первого начала термодинамики:
δQ dU δA.
dQ dU , т. к. dA 0
т.е. бесконечно малое приращение количества теплоты,
dQ равно приращению внутренней энергии dU.
Теплоемкость при постоянном объёме будет равна:
dQ dU μ
CV
.
dT
dT
ранее показано
2020 г. Чуев А.С.
i
CV R
2
8
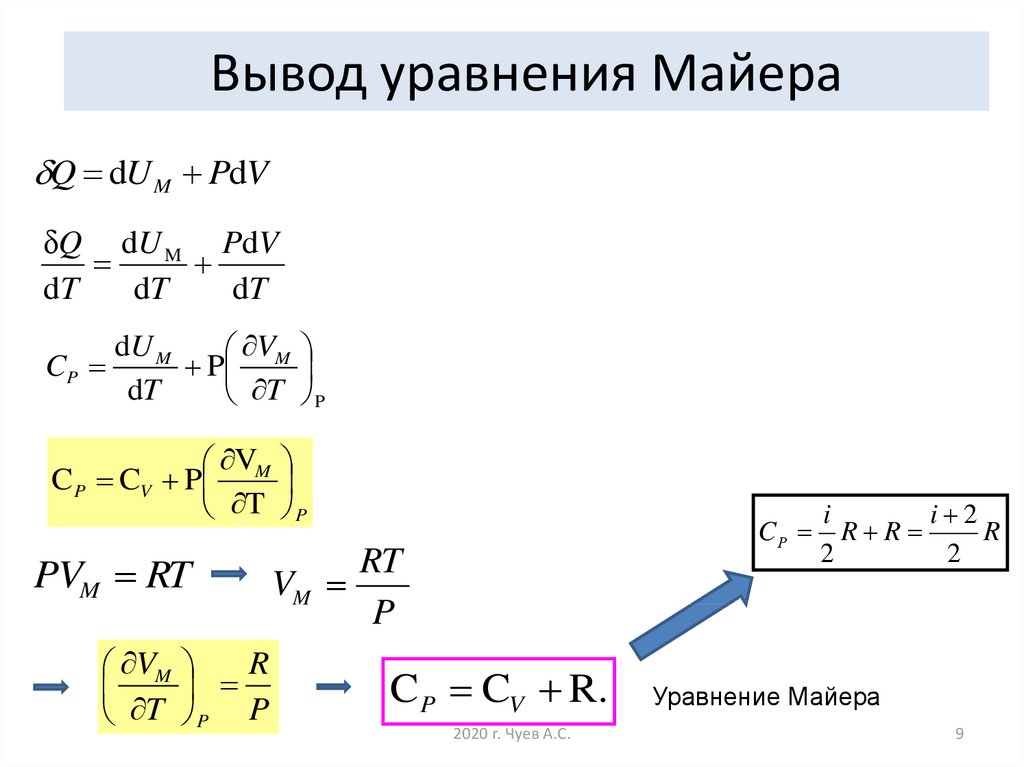
9. Вывод уравнения Майера
Q dU M PdVδQ dU M PdV
dT
dT
dT
dU M
VM
CP
P
dT
T P
V
C P CV P M
T P
PVM RT
R
VM
T P P
CР
RT
VM
P
C P CV R.
2020 г. Чуев А.С.
i
i 2
R R
R
2
2
Уравнение Майера
9
10. Это уравнение Майера для одного моля газа. Из него следует физический смысл универсальной газовой постоянной. R – численно
CP CV R.Это уравнение Майера для одного моля газа.
Из него следует физический смысл
универсальной газовой постоянной.
R – численно равна работе, совершаемой одним
молем идеального газа при нагревании на один
градус при изобарическом процессе.
Используя это соотношение, Роберт Майер в
1842 г. вычислил механический эквивалент
теплоты: 1 кал = 4,19 Дж.
2020 г. Чуев А.С.
10
11. Для произвольного количества газов: , Из теории следует, что СV не зависит от температуры. Однако это оказывается не верно при
Для произвольного количества газов:mi
CV
R
2 ,
m (i 2)
CP
R.
2
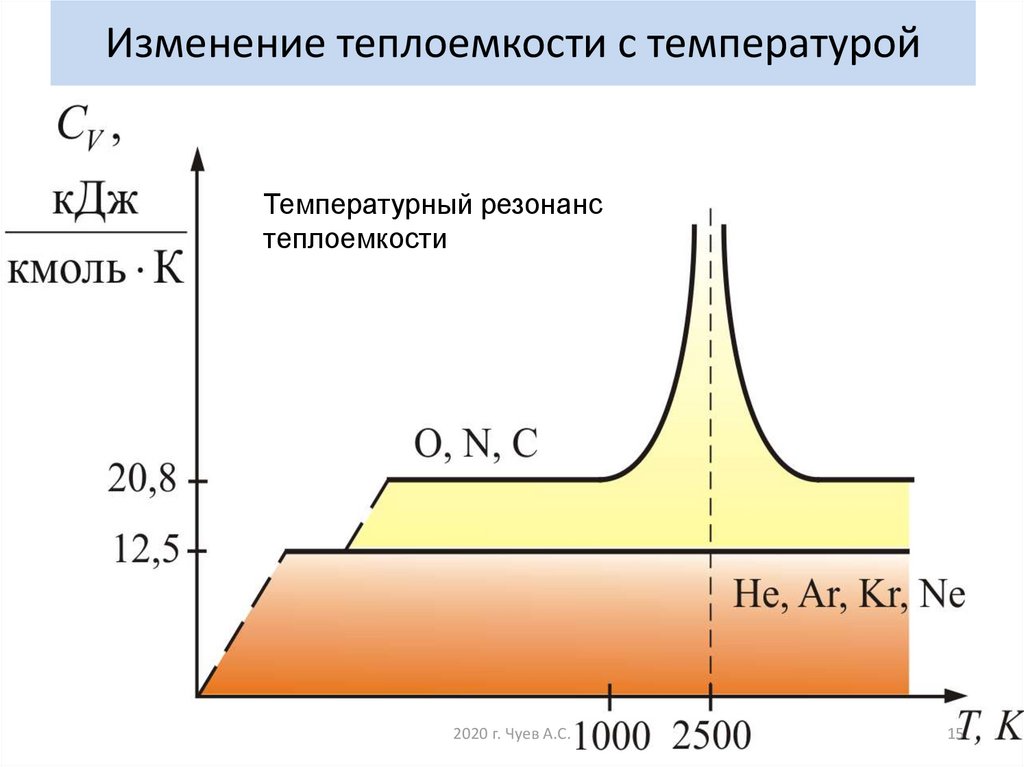
Из теории следует, что СV не зависит от
температуры. Однако это оказывается не верно при
больших температурах.
2020 г. Чуев А.С.
11
12. Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и т.п.), поэтому формула
Uμ CV T справедлива для любогопроцесса.
Для произвольной массы
идеального газа:
m
U CV T .
μ
2020 г. Чуев А.С.
12
13.
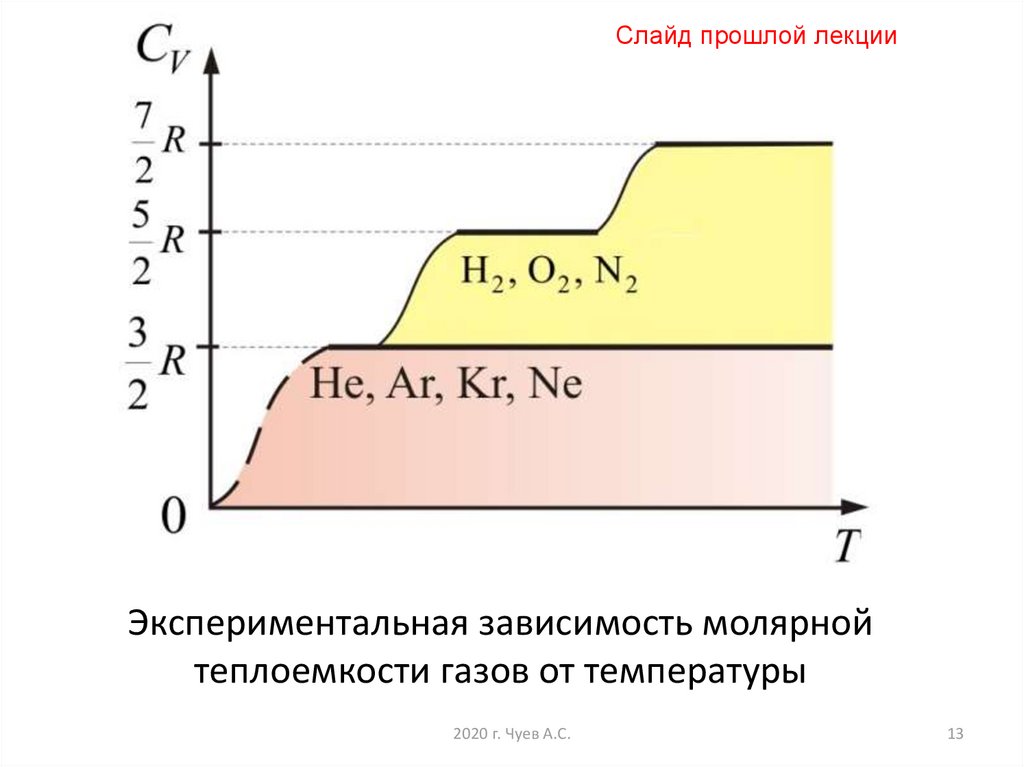
Слайд прошлой лекцииЭкспериментальная зависимость молярной
теплоемкости газов от температуры
2020 г. Чуев А.С.
13
14. Изменение теплоемкости с температурой
2020 г. Чуев А.С.14
15. Изменение теплоемкости с температурой
Температурный резонанстеплоемкости
2020 г. Чуев А.С.
15
16. Дискретные изменения энергии молекул
факультативноДискретные изменения энергии молекул
2020 г. Чуев А.С.
16
17. 3. АДИАБАТИЧЕСКИЙ ПРОЦЕСС. Уравнение Пуассона
Адиабатический процесс - процесс,происходящий без теплообмена с окружающей
средой.
Адиабатический по иному изоэнтропийный
процесс (ΔS = 0, S = const).
2020 г. Чуев А.С.
17
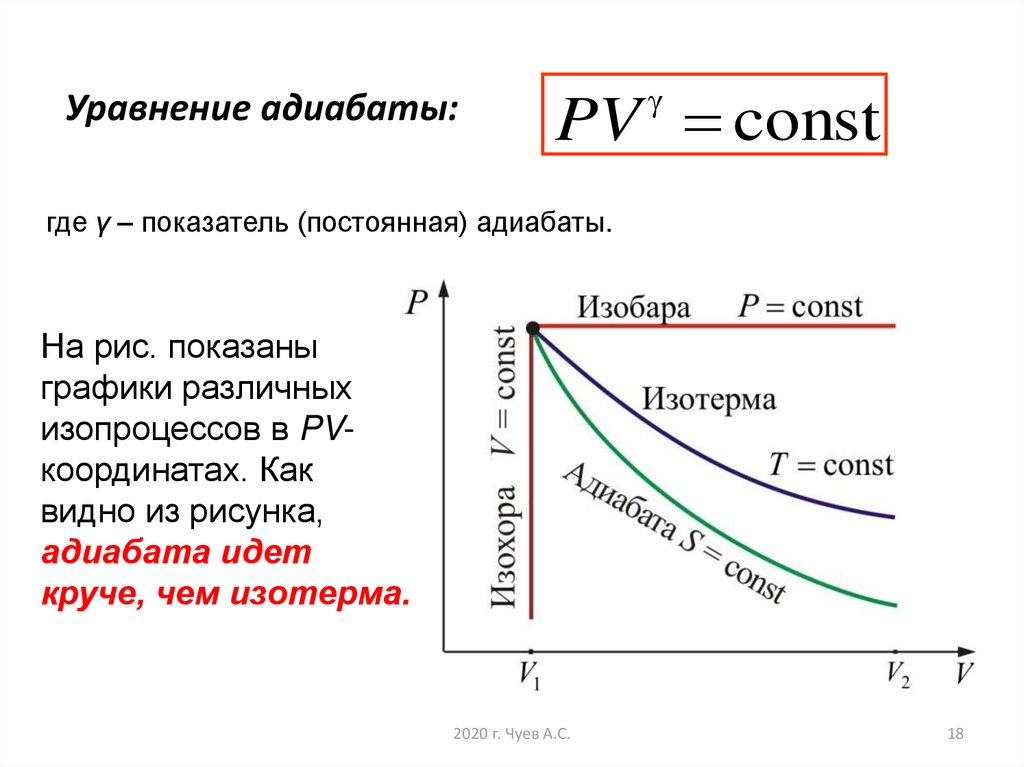
18. Уравнение адиабаты:
PV constгде γ – показатель (постоянная) адиабаты.
На рис. показаны
графики различных
изопроцессов в PVкоординатах. Как
видно из рисунка,
адиабата идет
круче, чем изотерма.
2020 г. Чуев А.С.
18
19. Адиабатический процесс характеризуется показателем адиабаты
γПоказатель адиабаты зависит от i, то есть строения молекул:
2020 г. Чуев А.С.
19
20.
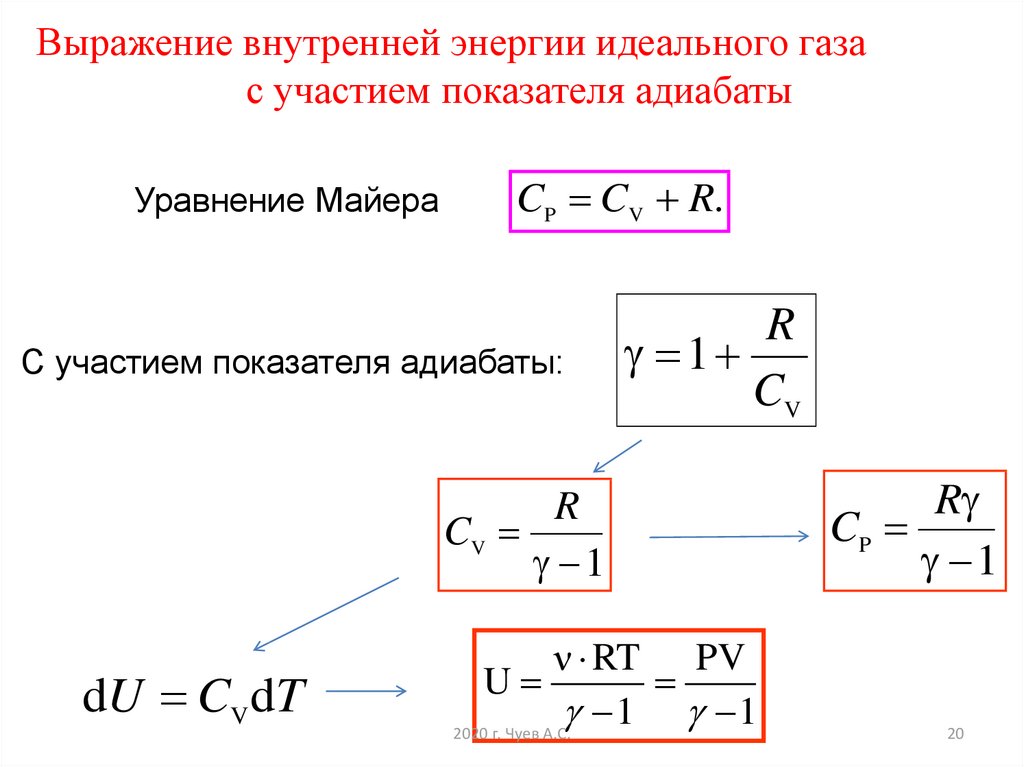
Выражение внутренней энергии идеального газас участием показателя адиабаты
Уравнение Майера
CP CV R.
С участием показателя адиабаты:
R
1
CV
R
CV
1
dU CV dT
ν RT PV
U
1 1
2020 г. Чуев А.С.
R
CP
1
20
21. Вывод уравнения адиабаты
Из первого начала ТД, с учетом:RT
PV
U
γ 1 γ 1
PV
Q d
PdV
1
d( PV ) ( 1) PdV VdP PdV PdV PdV 0
VdP PdV 0
dP
dV
0
P
V
ln V ln P c
разделим на
PV
d(ln V ) d(ln P) 0
PV const
2020 г. Чуев А.С.
Уравнение
Пуассона
21
22. - постоянная адиабаты (коэффициент Пуассона)
СРγ,
СV
Сделав подстановки из
PV const
в
vRT γ
PV
V ~
V
γ
PV TV
γ
γ 1
- постоянная адиабаты
(коэффициент Пуассона)
PV vRT
его можно преобразовать:
TV
vRT
T
P
1
const
γ 1
1
~P1 T TP
2020 г. Чуев А.С.
const
22
23.
2020 г. Чуев А.С.23
24.
Работа при адиабатическом процессеПоложительная работа осуществима лишь за счет
уменьшения внутренней энергии
При
А dU
Q 0
R
А νCV T2 T1 ν
(T1 T2 )
1
С учетом:
T1V1
1
P1V1 T2
1
1 T1
T2V ; PV P1V1
1
2
и
P1V1 νRT1
уравнение для работы можно преобразовать, придав иной вид:
P1V1 V1
А
1
1 V2
1
1
PV
P
1 1 1 2
1 P1
2020 г. Чуев А.С.
γ 1
V1
νRT1
1
γ 1 V2
24
25.
4. Политропический процесс.Процесс, при котором теплоёмкость газа
остаётся постоянной. С = const.
Политропический процесс – самый общий из всех
изопроцессов.
Уравнение политропы:
PV const
n
где n – показатель политропы
2020 г. Чуев А.С.
25
26. Вывод уравнения политропы
Для моляCdT CV dT PdV
PV RT
(1)
дифференцируем , получая
PdV VdP
dT
R
PdV VdP RdT
подставляем в (1)
(C CV )( PdV VdP) RPdV
(C CV R) PdV (С CV )VdP 0
Заменим
(CV R)
на
CP
и разделим на
dV
dP
(C CP )
(C CV )
0
V
P
PV
проинтегрируем
(C CP ) ln V (C CV ) ln P const
2020 г. Чуев А.С.
26
27. продолжение вывода уравнения политропы
Разделим все на(C CV )
тогда при
C CV
(C CP )
ln V ln P const
(C CV )
PV const
n
где
C CP
n
C CV
2020 г. Чуев А.С.
Уравнение
политропы
– показатель политропы
27
28.
Отсюда можно получить:nCV CP
С
n 1
Уравнение политропы преобразуемо :
PV const
n
TV
n 1
по аналогии с преобразованием уравнения
адиабаты выводится
const P T TP
Если уравнение
1 n
n
n PdV VdP 0
1 n
n
const
умножить на
C CV
То получим уравнение политропы в дифференциальном виде:
(С CP ) PdV (C CV )VdP 0
2020 г. Чуев А.С.
28
29.
Выводы из последнего уравнения:При
C CV
Отсюда :
(С CP ) PdV 0
dV 0
V const
и
Аналогичный вывод делается при
C CP
Тогда
dР 0
и
Р const
2020 г. Чуев А.С.
29
30.
Работа ИГ в политропических процессахПолитропный:
Формула: 1)
V2
2) А1 2 PdV .
т. к.
PV n P1V1 P2V2 ;
n
V1
V2
А1 2
dV
PV n
V
V1
n
1 1
А1 2
При
n 1
P P1V1 / V
n
n
n
dV
1 1
1
V V n n 1 V1n 1 V2n 1
1
V2
n 1
RT1 V1
V1
P1V1
1
1
n 1 V2
n 1 V2
n 1
Формула 2 применима при расчетах изотермических процессов.
2020 г. Чуев А.С.
30
31.
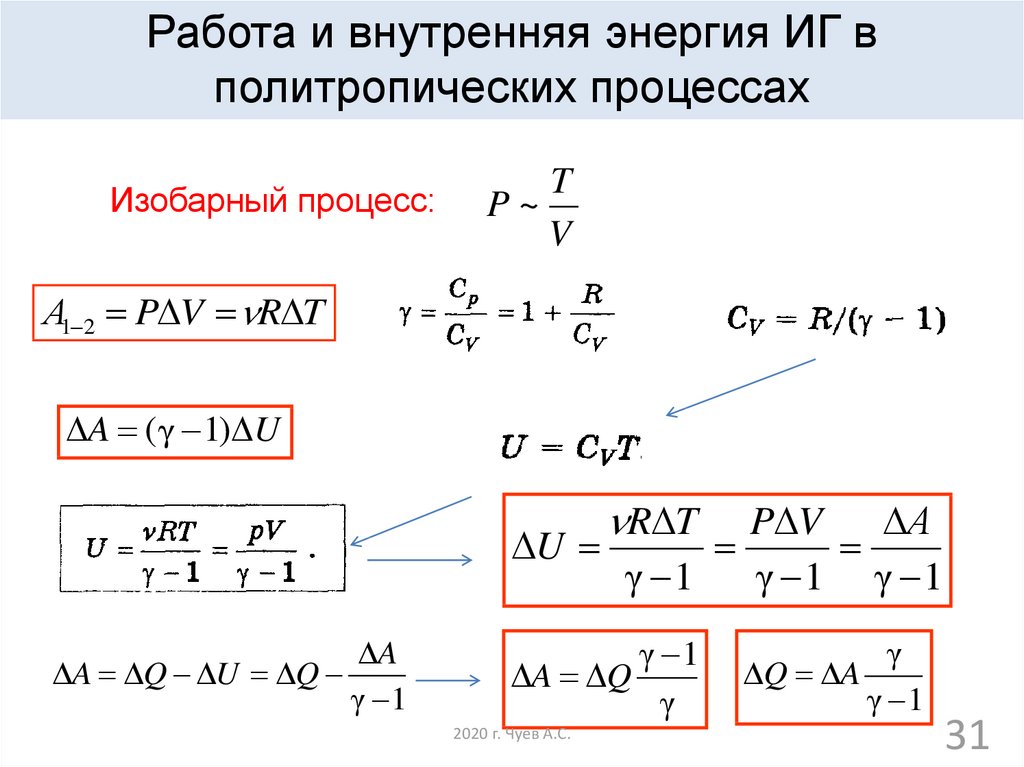
Работа и внутренняя энергия ИГ вполитропических процессах
Изобарный процесс:
T
P~
V
А1 2 P V R T
A ( γ 1) U
R T
P V
А
U
γ 1
γ 1 γ 1
A
A Q U Q
γ 1
γ 1
A Q
γ
2020 г. Чуев А.С.
γ
Q A
γ 1
31
32.
Работа и внутренняя энергия ИГ вполитропических процессах
Изотермический:
A Q
V2
dV
А1 2 P1V1 n
V V
n
1
n 1
U 0
V2
А1 2
dV
V2
νRT
νRT ln
V
V1
V1
Изохорный:
А 0
V P νR T
U Q
1 1
2020 г. Чуев А.С.
32
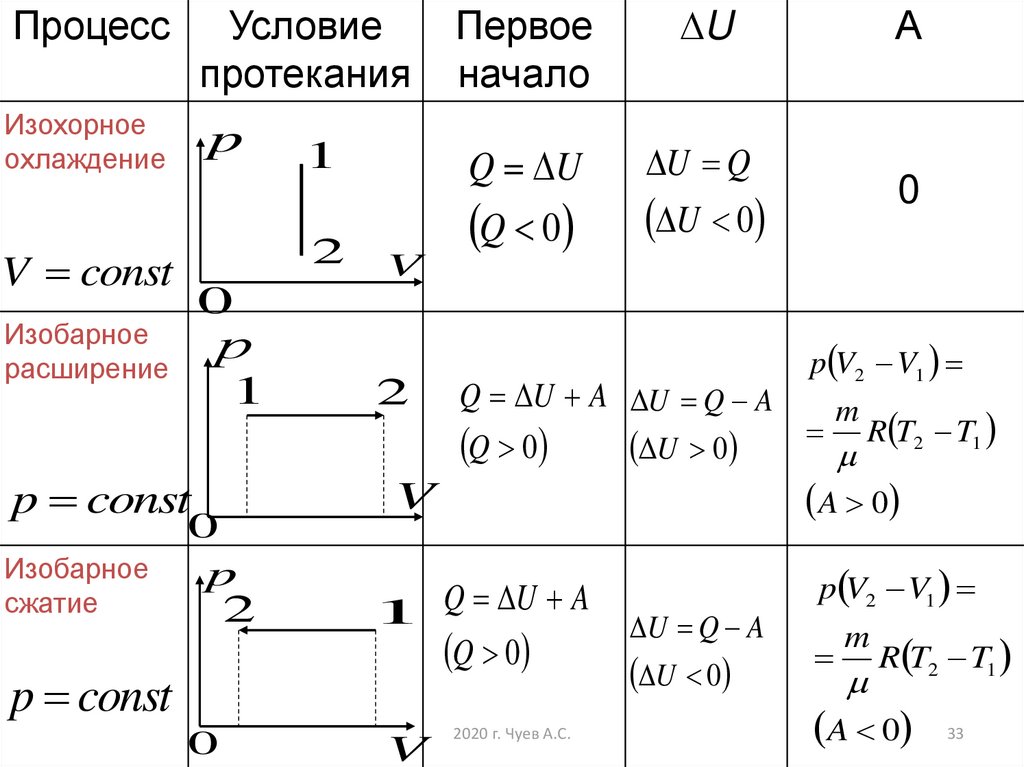
33.
ПроцессУсловие
протекания
Изохорное
охлаждение
p
2
V const
U
Q U
U Q
Q 0
А
0
U 0
V
0
Изобарное
расширение
р
1
p const
Изобарное
сжатие
1
Первое
начало
0
p
2
p const
0
2
p V2 V1
Q U A U Q A
m
R T2 T1
Q 0
U 0
A 0
V
1 Q U A
Q 0
V
2020 г. Чуев А.С.
U Q A
U 0
p V2 V1
m
R T2 T1
A 0
33
34.
Рекомендуется законспектировать2020 г. Чуев А.С.
34
35.
конспектироватьПоказатель политропы и теплоемкость в
изопроцессах
2020 г. Чуев А.С.
35
36.
факультативноn
n 0
2020 г. Чуев А.С.
36
37.
Газ Ван-дер-ВаальсаУравнение Ван-дер-Ваальса для произвольного
количества вещества реального газа учитывает
конечный
объем
молекул
b
и
их
взаимодействие между собой 2a/V2:
ν a
P 2 (V νb) νRT
V
2
где а и b – постоянные Ван-дер-Ваальса
V – объем, занимаемый газом;
P – давление газа на стенки сосуда.
2020 г. Чуев А.С.
37
38. Поправка касается давления. Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления P*
ν 2a2
V касается
Поправка
давления.
Межмолекулярное притяжение эквивалентно
существованию
в
газе
некоторого
внутреннего давления P* (иногда его
называют статическим давлением).
Поправка b в уравнении состояния
идеального газа учитывает собственный
объем, занимаемый молекулами реального
газа.
2020 г. Чуев А.С.
38
39. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени
Согласно модели Ван-дер-Ваальса, силыпритяжения между молекулами (силы Ван-дерВаальса) обратно пропорциональны шестой
степени расстояния между ними, или второй
степени объема, занимаемого газом. Считается
также, что силы притяжения суммируются с
внешним давлением.
2020 г. Чуев А.С.
39
40. Внутренняя энергия газа Ван-дер-Ваальса
Внутренняя энергия газа Ван-дерВаальсаЭнергия одного моля газа Ван-дер-Ваальса
слагается из:
•внутренней энергии молекул газа;
• кинетической энергии теплового движения
T
центра масс молекул
Ek CV dT
0
•потенциальной энергии взаимного притяжения
молекул
En a / Vm
41. Избыточное внутреннее давление Pi пропорционально квадрату концентрации числа частиц Pi ~ nS nV ~ N 2/V 2, где N – полное число
частиц в сосуде объема V.Если N = NA – в сосуде находится один моль
газа, то:
Pi = a/V 2,
где а – постоянная величина, своя для каждого
сорта газа.
В случае -молей Pi = 2a/V 2.
2020 г. Чуев А.С.
41
42. Дополнительное давление газа Ван-дер-Ваальса за счет взаимного притяжения молекул равно a/Vm2, тогда потенциальная энергия
Дополнительное давление газа Ван-дерВаальса за счет взаимного притяжениямолекул равно a/Vm2, тогда потенциальная
энергия данного взаимодействия равна
En
a / V dV
Vm
2
m
m
a / Vm
En a / Vm
Vm – молярный объем: Vm = V/ , = m/ .
Знак «минус» указывает на то, что между
молекулами действуют силы притяжения.
2020 г. Чуев А.С.
42
43.
Внутренняя энергия реального газа наряду скинетической энергией хаотического движения
частиц СVT включает и потенциальную энергию
их притяжения a/Vm
a
U ν CV T
Vm
где СV – молярная
постоянном объеме.
теплоемкость
2020 г. Чуев А.С.
газа
при
43
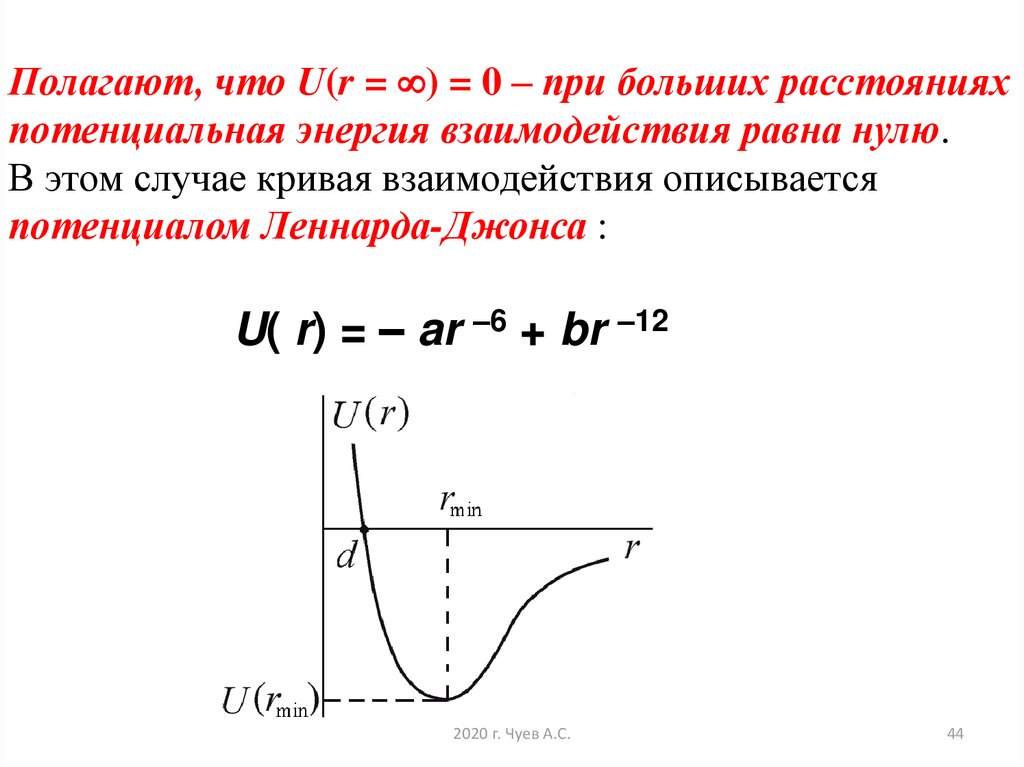
44. Полагают, что U(r = ) = 0 – при больших расстояниях потенциальная энергия взаимодействия равна нулю. В этом случае кривая
Полагают, что U(r = ) = 0 – при больших расстоянияхпотенциальная энергия взаимодействия равна нулю.
В этом случае кривая взаимодействия описывается
потенциалом Леннарда-Джонса :
U( r) = – ar –6 + br –12
2020 г. Чуев А.С.
44
45.
2020 г. Чуев А.С.45
46. Конец лекции 12
2020 г. Чуев А.С.46






































 physics
physics