Идеальный газ. Теплоемкость. Термодинамика.Энтропия

1.

General Physics NRNU MEPhI
Молекулярная физика.
Лекция 04 (07)
24 марта 2021
Идеальный газ. Теплоемкость.
Термодинамика.Энтропия
Лектор: доцент НИЯУ МИФИ,
Андрей Станиславович ОЛЬЧАК

2.

Уравнение состояния идеального газа
Основное уравнение МКТ: Р = nkT
Оно-же - уравнение Менделеева-Клапейрона:
РV = nkTV = νRT = (M/μ)RT
где R = kNA = 8,3 Дж/моль•К - универсальная газовая
постоянная
Температура – мера средней кинетической энергии
движения молекул
T = Θ/k - абсолютная температура, измеряемая в градусах
Кельвина [K]; Θ - термодинамическая температура,
измеряемая в Джоулях; k = 1,38 х 10-23 Дж/К
<Ek> = m<v2>/ 2 =3Θ / 2m = 3kT/2

3.

Число степеней свободы и способов накопления
энергии многоатомной молекулы
Молекула
жесткая
i = nпост+nколеб
i 3пост 2вращ 5
i 3пост 3вращ 6
упругая
i nпост nвращ 2nколеб
nколеб 3N 5
i= 6N - 5
nколеб 3N 6
i= 6(N – 1)

4.

Равнораспределение энергии по степеням свободы
Основное допущение статистической термодинамики:
огромное числа хаотических соударений и обменов энергией между
молекулами приводит к равномерному ее распределение по всем
возможным степеням свободы (способам накопления энергии)
причем на каждый способ приходится энергия, равная
Средняя энергия одной молекулы
kT/2
i
kT
2
i nпост nвращ 2nколеб
Колебательные степени свободы учитываются дважды, поскольку
колебательному движению соответствует как кинетическая,
так и потенциальная энергии

5.

Равнораспределение энергии по степеням свободы
На каждую «степень свободы» i приходится энергия kT/2
Средняя энергия одной молекулы:
i
kT
2
i nпост nвращ 2nколеб
При нормальных температурах для одноатомного идеального газа i
= 3, для двухатомного i = 5
Внутренняя энергия одного моля «идеального» газа (когда можно
пренебречь потенциальной энергией взаимодействия молекул)
i
i
U м N A kN AT RT
2
2
Внутренняя энергия произвольного количества идеального газа:
U = ivRT/2

6.

Теплоемкость
Чтобы нагреть тело массы m от температуры Т1 до температуры Т1+dT
надо передать ему количество теплоты
dQ = СmdТ > 0
При охлаждении тело отдает то же количество теплоты (dQ < 0 ) .
С = dQ/mdТ - удельная теплоемкость тела, т.е. количество теплоты,
(Дж) которое получает (или отдает) 1 кг вещества при нагревании (или
охлаждении) на 1 К
[C] = [ Дж/кг•К ]
Сμ = μdQ/mdT - молярная теплоемкость тела, т.е. количество теплоты,
(Дж) которое получает (или отдает) 1 моль вещества при нагревании
(или охлаждении) на 1 К [Cμ] = [ Дж/моль•К ]

7.

Теплоёмкость. Изопроцессы
dQ = dU + dAгаза = ivRdT/2 + PdV
cμ = dQ/vdT = iR/2 + PdV/vdT;
УМК: PV = vRT =>
Изотермический процесс: T=const.; dU = 0; dQ = PdV = 0
cμT = dQ/vdT = ∞
Изохорный процесс: V = const.; dA = 0; dU = dQ
/
cμV = dU/vdT = iR/2
Изобарный процесс: P = const.; dA = PdV = vRdT
cμP = iR/2 +R = (i+2)R/2
Адиабатный процесс: dQ = 0 (теплоизолированная система)
cμQ = dQ/vdT = 0
C
i 2 показатель
P
CV
i адиабаты

8.

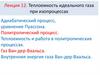
Теплоемкость идеального газа
Молекула
Характер связи
Число
степеней
свободы
поступат
вращат.
колебат.
i
CV
CP
–
3
3
R
2
5
R
1,67
2
–
5
R
5 2
7
R
1,40
2
1+1
7
R
7 2
9
R
2 1,29
–
6
R
6 2
8
R
2
1,33
.
Одноатомная
Двухатомная
Двухатомная
–
Жесткая
Упругая
3
3
3
–
2
2
С числом
атомов
три и более
Жесткая
3
3

9.

Уравнение адиабаты для идеального газа
Уравнение адиабаты для идеального газа

10.

Уравнение адиабаты для идеального газа
Адиабатическим называется процесс, который происходит
без теплообмена с окружающей средой
dQ = dU + dAгазa = ivRdT/2 + PdV = 0
PV = vRT => P = vRT/V
ivRdT/2 + vRTdV/V= 0 => dT/T + 2dV/iV = 0 =>
lnT + (2/i)lnV = ln(TV2/i) = Const
TV2/i = Const
γ =(i+2)/i = 1 + 2/i => 2/i = γ - 1
TV
1
const

11.

Уравнение адиабаты для идеального газа
Адиабатическим называется процесс, который происходит
без теплообмена с окружающей средой
TV
1
const
уравнение адиабаты идеального газа
в переменных T и V
pV
T
R
pV const
Tγ
V1-γ
= Const
уравнение адиабаты идеального газа в
переменных p и V – уравнение
Пуассона
уравнение адиабаты идеального газа в
переменных p и T – уравнение
Пуассона

12.

Уравнение адиабаты для идеального газа
pV const
P
Изотерма
Адиабата
P V
P0
V0
V
1
dV V dp 0
dp
p
dV
V
уравнение изотермы идеального газа
pV const
PdV Vdp 0
dp
p
dV
V

13.

Уравнение политропы для идеального газа
Уравнение политропы для идеального газа

14.

Политропный процесс
Во всех изо-процессах теплоемкость остается постоянной и равной
численной константе, умноженной на универсальную газовую
постоянную R. Сμ/R = Const
Также остается постоянной комбинация параметров
где число n называется показателем политропы.
Процесс
Изохорный
Изобарный
Изотермический
Адиабатический
Теплоемкость
сμ/R
i/2
i/2 + 1
∞
0
PVn = Сonst,
.
Постоянная политропы
n
V = const = P0V => (P0V)1/0 = PV∞ => n=∞
P = Const = PV0 => n = 0
PV = vRT = Const => n = 1
PVγ = Const => n = γ
Процессы, где остаются постоянными Сμ/R и PVn называются политропными.
.

15.

Политропный процесс
Политропный процесс = процесс, протекающий с постоянной
теплоемкостью. Убедимся, что процесс, в котором PVn = Сonst, будет
иметь постоянную теплоемкость при любом значении n,
Связь показателя политропы n и теплоемкости. .
cμ (n) = dQ/dT = R(i/2 +1/(1-n)) = сV - R/(n-1)
Проверим:
n = 1 (изотерма => cn = R(i/2 +1/(1-1)) -> ∞
n = γ = 1+2/i (адиабата => cn = R(i/2 +i/2) = 0
n = 0 (изобара => cn = R(i/2 +1)
n = ∞ (изохора => cn = Ri/2
Все результаты - правильные!:

16.

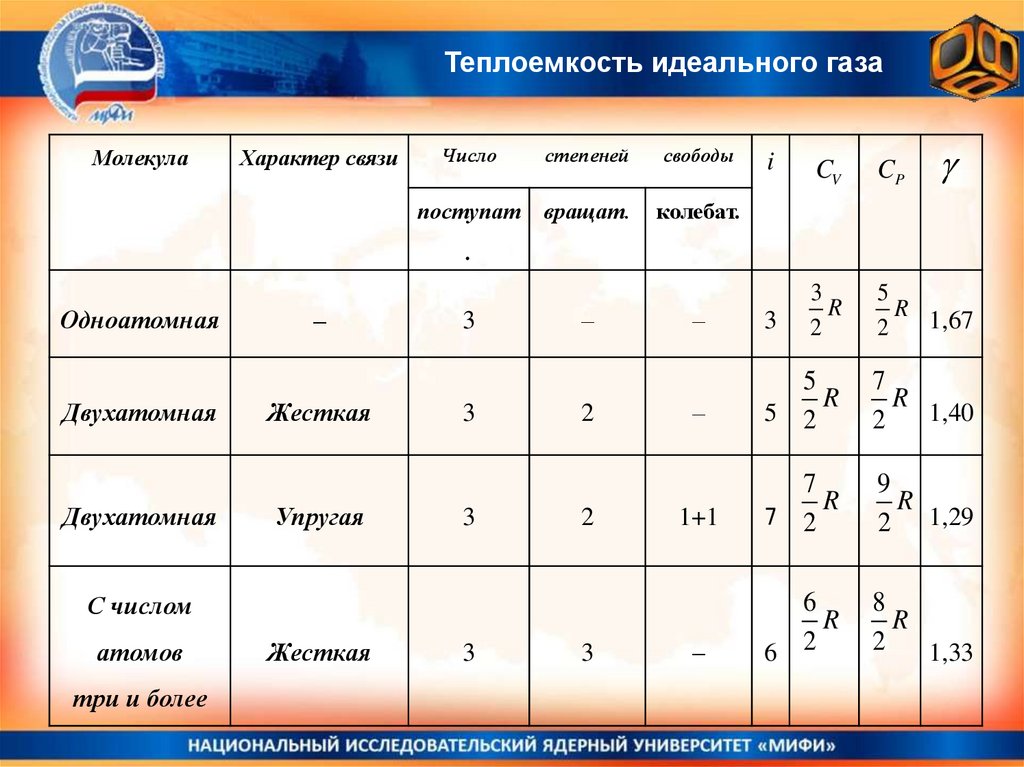
Политропный процесс
R
C ( n ) CV
n 1
PVn= Const
CV = iR/2
CP i 2
CV
i
Процесс
n
k=C/R
0
γ = (i+2)/i
1
∞
Изотермический
γ
0
Адиабатический
±∞
i/2
Изобарный
Изохорный

17.

Политропный процесс
A12
pV p V p V
n
n
1 1
n
2 2
n 1
V2
pdV
V1
n
1 1
n
pV
P
V
dV
A12 p V n
V
V1
dV
1 1
1
V V n n 1 V1n 1 V2n 1
1
V2
n 1
V1
p1V1
A12
1
n 1 V2
pV
1 1 RT1
V2
n 1
V1
RT1
A12
1
n 1 V2
n
1 1

18.

Разные процессы – работа газа
при адиабатическом процессе:
1
RT1 V1
A12
1
1 V2
V2
dV
A12 p V n
V
V1
n
1 1
n 1
V1
RT1
A12
1
n 1 V2
при изотермическом процессе:
V2
dV
V2
A12 RT
RT ln
V
V1
V1
pV
1 1 RT1
Процесс
n
C
A12 p(V2 V1 )
0
CP
Изобарный
1
∞
Изотермический
при изохорном процессе:
γ
0
Адиабатический
при изобарном процессе:
dV 0
A12 0
±∞
CV
Изохорный

19.

Энтропия в термоднамике
Энтропия в термодинамике

20.

Макропараметры
ВСПОМНИМ!
Газы в макроскопических количествах состоят из огромного
числа молекул. Для практического описания состояний
газов, близких к идеальному, используется всего несколько
усредненных макро-параметров:
V [м3] – объем
M [кг] - масса; ρ[кг/м3] = M/V – плотность вещества
P [Н/м2] – давление
T [К] – температура
μ [г/моль] – молярная масса; ν [моль] = M/μ = количество вещества
S – энтропия – что это такое?

21.

Энтропия в термодинамике
Энтропия появилась в термодинамике для характеристики
не состояний, а процессов: если в процессе система
получает теплоту dQ при температуре
энтропии системы называют отношение
T, то приращением
dS = dQ/T [Дж/K]:
T
S2
Q T S dS
S
S1
S1
S2
TdS = dQ = dU + dA = (ivR/2)dT + PdV

22.

Энтропия в термоднамике
dS =dQ/T = dU/T + dA/T = (ivR/2)dT/T + PdV/T
В расчете на один моль вещества приращение энтропии составляет:
dS = (iR/2)(dT/T) + (P/T)dV = (iR/2)(dT/T) + (R/V)dV =
= (iR/2)(dT/T) + R(dV/V) = Rd(lnTi/2V) =>
S =Rln(Ti/2V)+Const =CVlnT +RlnV+Const
Энтропия как параметр состояния определяется в термодинамике с
точностью до постоянной (подобно потенциальной энергии в механике).
Для произвольного количества вещества
S=vRln(Ti/2V)+Const = v(CVlnT +RlnV) + Const
“Энтропия аддитивна, подобно внутренней энергии системы.

23.

Энтропия в термоднамике
Уравнение состояния идеального газа PV = vRT позволяет переписать
выражение для энтропии через разные параметры
S= vRln(Ti/2V)+Const = v(СVlnT+RlnV)+Const
S=vRln(T(i+2)/2/P)+Const = v(СPlnT-RlnP)+Const
S=vRln(Pi/2V(i+2)/2)+ Const = v(СPlnV+СVlnP)+Const
Зачем нужна (чем полезна) энтропия в термодинамике?
• Энтропия характеризует степень беспорядка в термодинамической
системе
• Энтропия помогла красиво построить теорию тепловых машин
• Энтропия помогает разобраться в отличиях обратимых и необратимых
процессов в термодинамике
• В статистической физике выявляется глубокий физический смысл
понятия энтропии, по сей день обсуждаемый
“.

24.

Энтропия и внутренняя энергия
Математически энтропия, как правило, выражается функцией двух
параметров
S(T, V), или S(T, P), или S(P,V)
Поскольку U
= ivRT/2 , энтропию можно выразить, например, через
объем V и внутреннюю энергию U
S(V, T) = vRlnV + vCVlnT + Const =>
S(V, U) = vRlnV + vCVlnU + Const’ ; Const’ = Const + vCVln(ivR/2)
Математически дифференциал от любой функции любых двух переменных
df(x,y)=(df/dx)y dx+(df/dy)x dy
Полный дифференциал
энтропии как функции
внутренней энергии и объема:
S S U , V
S
S
dS
dU
dV
U V
V U

25.

Энтропия в термодинамике
Полный дифференциал
энтропии как функции
внутренней энергии и объема:
S S U , V
S
S
dS
dU
dV
U V
V U
По определению энтропии и из первого начала термодинамики следует:
dS = dQ/T = dU/T + PdV/T
Сравнивая два дифференциала, находим:
1 S
T U V
S
p T
V U

26.

Энтропия и термодинамика
ПРИМЕР: теплообмен между двумя частями теплоизолированного сосуда
T1
<
T2
S S1 U1 S2 U 2
dS1
dS2
dS1 dS2
dS
dU1
dU 2 dU1 /T1 + dU2/T2
dU1
dU 2
T1
T2
1 1
U U1 U 2 const dU1 dU 2 dS dU1 0
T1 T2
Если T2 T,1 то dU1 0.
Тепло (внутренняя энергия) передается от более
нагретого газа к менее нагретому. При этом общая
энтропия системы возрастает

27.

Энтропия и термодинамика
ЕЩЕ ПРИМЕР: Смешивание разных газов в теплоизолированном сосуде
T1 T2 , 1 2
S ?
V1 V2
V1
V2
Q 0, A 0 U 0, T const
S= v(СVlnT+RlnV) =>
S 2 R ln V1 V2 R ln V1 R ln V2 R ln
V1 V2
VV
1 2
2
0
Ничего не изменилось – v, V, T, P – все остается прежним, НО(!) –
возрос беспорядок и энтропия системы
Энтропия – мера беспорядка! …

28.

Приращение энергии и теплота
И ЕЩЕ ПРИМЕР:
Расширение идеального
газа в пустоту в
теплоизолированном
сосуде.
d Q 0,
V растёт
S растёт
Для необратимых процессов всегда
dS 0
d Q
dS
T
TdS pdV dU
Неравенство Клаузиуса – для циклических процессов
d Q
T
dS 0
d Q
0
T
d Q
dS
T

29.

2-е начало термодинамики
– формулировки Кельвина и Клаузиуса
При любых процессах в изолированной системе
её энтропия не убывает. СЛЕДСТВИЯ:
1.
2.
Нельзя осуществить процесс,
единственным конечным результатом
которого будет переход теплоты от
менее нагретого тела к более нагретому
(Р. Клаузиус, 1850).
Р. Клаузиус
Нельзя осуществить процесс,
единственным конечным результатом
которого будет превращение некоторого
количества теплоты полностью в работу
(Лорд Кельвин, 1851).
Лорд Кельвин (У. Томсон)

30.

Второй закон термодинамики
Предоставленная сама себе, система ВСЕГДА переходит из
более упорядоченного в менее упорядоченное (и оттого
более вероятное) состояние. При этом энтропия системы
возрастает. Самое вероятное состояние – равновесное,
с максимальной энтропией
В ЧАСТНОСТИ: При контакте двух тел, теплота ВСЕГДА
переходит от более нагретого тела к менее нагретому,
приводя тела в тепловое равновесие.
Первый закон термодинамики (закон сохранения энергии)
отражает общность механики и термодинамики.
Второй закон термодинамики отражает РАЗНИЦУ механики
и термодинамики.

31.

2-е начало термодинамики
– невозможность вечного двигателя
Первый закон термодинамики (закон сохранения энергии) –
запрещает возможность извлечения энергии из ничего.
Вечный двигатель первого рода (работающий без
источников энергии) НЕ ВОЗМОЖЕН
Второй закон термодинамики запрещает возможность
существования и вечного двигателя второго рода, который
превращал бы в работу ВСЁ тепло, извлекаемое из
окружающих тел (КПД=100%).

32.

2-е начало термодинамики
– невозможность вечного двигателя
Демон Максвелла сортирует
«горячие» и «холодные» молекулы,
что позволяет нагреть правую часть
сосуда и охладить левую без
дополнительного подвода энергии к
системе. Энтропиясистемы в
начальном состоянии больше, чем в
James Clerk Maxwell, 1831-79
конечном.
«Неизбежное увеличение беспорядка (энтропии) с
течением времени – это одно из определений т. н.
«стрелы времени», т. е. возможности отличить
прошлое от будущего, определить направление
времени»
(Stephen Hawking. 1942-2016)
Энтропия – это до сих пор таинственно…
Энтропия – это таинственно и «круто»!

33.

Курс общей физики НИЯУ МИФИ
Тепловые машины

34.

Тепловые машины
Тепловая машина (двигатель) = устройство, совершающее механическую
работу за счёт теплоты, получаемой от внешних источников.
Тепловой машине нужно рабочее вещество (газ или жидкость),
которое совершает термодинамический цикл:
(нагревание>расширение>охлаждение>сжатие).
При нагревании рабочему веществу сообщается теплота Q1.
При охлаждении часть теплоты Q2 отбирается . .
По закону сохранения энергии, рабочее вещество способно совершить
работу A = Q1.- Q2 . Коэффициентом полезного действия (К.П.Д. = η)
тепловой машины называется отношение полезной работы А к
затраченной энергии Q1:
η = А/Q1 = (Q1 - Q2)/Q1

35.

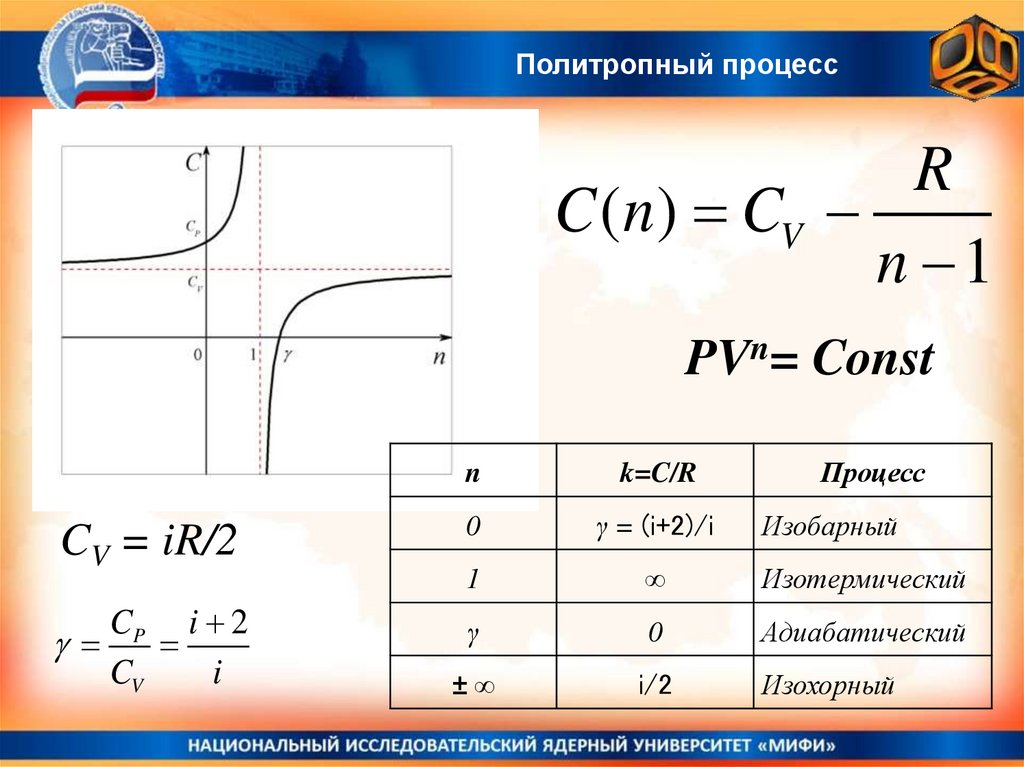
Тепловые машины
Цикл работы теплового двигателя.
Работа А = Q1-Q2
Тх -> Tн
Тн
КПД: η = А/Q1 = (Q1-Q2)/Q1 <1
Тн -> Tх
Расширение при
нагревании до Тн
Теплота Q1 от нагревателя
с температурой
Тн
Тх
Сжатие при
охлаждении до Тх
Теплота Q2 отдается
“холодильнику” с температурой
Тх

36.

Тепловые машины. Цикл Карно
Цикл Карно это обратимый цикл, состоящий из
двух изотерм и двух изоэнтроп (адиабат).
dS = dQ/T = 0
A Q1 Q2
2
T
Tн
Tх
1
3
4
S
Sadi Carnot
1796-1832
S
Цикл Карно в переменных T , S
1 2 и 3 4 изотермы, 2 3
и 3 4 адиабаты
Цикл Карно идеального газа

37.

Тепловые машины. Цикл Карно
A Q1 Q2
2
T
Tн
1
dS = dQ/T = 0
Tх
3
4
S
S
Теорема Карно ( 1824). К.П.Д. тепловых машин, использующих цикл
Карно рабочего вещества, максимален и не зависит от природы
T
рабочего вещества и конструкции машины. Его величина равна 1 х
Найдем КПД:
Q2
Tх S
Tх
A
1
1
1
Q1
Q1
Tн S
Tн
Tн

38.

Тепловые машины. Цикл Карно
A Q1 Q2
2
T
Tн
1
dS = dQ/T = 0
Tх
3
4
S
S
Теорема Карно ( 1824). К.П.Д. тепловых машин, использующих цикл
Карно рабочего вещества, максимален. Как доказать это?
Простейший способ: при фиксированной температуре нагревателя и
холодильника, при заданных значениях начального и конечного
состояний – максимально возможная работа (площадь внутри графика
процесса) – если процесс занимает все пространство между
указанными пределами. – (прямоугольник на диаграмме ST)

39.

Тепловые машины. Цикл Карно
Более формальный способ: применим неравенство Клаузиуса)
0
d Q1
d Q2
d Q1
d Q2 Q1 Q2
d Q
T
T
T
Tн 1 Tх
Tн Tх
1
2
1
Здесь 1 полученная за цикл теплота; 2 отданная за цикл теплота.
Q1 Q2
T Q2
T T
T Q
х1
T н Qх 2
н
1 1
T х Q1
н

40.

Дистанционный курс общей физики НИЯУ МИФИ
Основы молекулярной и статистической
физики
Лекция 04
Спасибо за внимание!