Идеальный газ. Теплоемкость. Термодинамика

1.

General Physics NRNU MEPhI
Молекулярная физика.
Лекция 03 (06)
17 марта 2021
Идеальный газ. Теплоемкость.
Термодинамика.
Лектор: доцент НИЯУ МИФИ,
Андрей Станиславович ОЛЬЧАК

2.

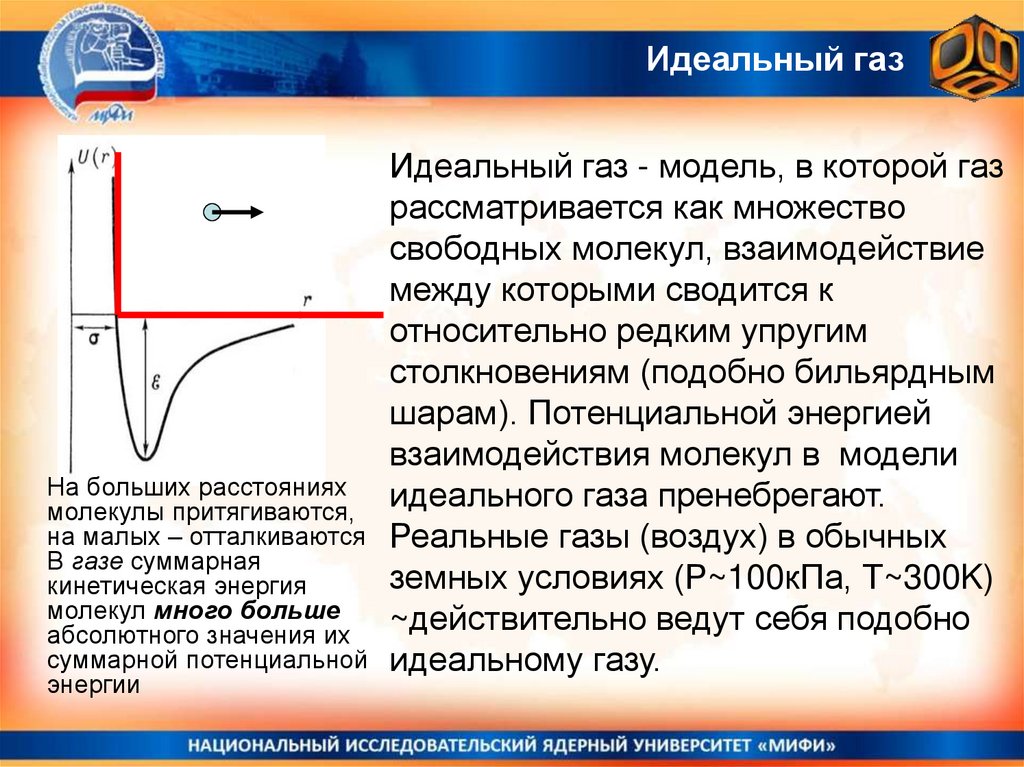
Идеальный газ
На больших расстояниях
молекулы притягиваются,
на малых – отталкиваются
В газе суммарная
кинетическая энергия
молекул много больше
абсолютного значения их
суммарной потенциальной
энергии
Идеальный газ - модель, в которой газ
рассматривается как множество
свободных молекул, взаимодействие
между которыми сводится к
относительно редким упругим
столкновениям (подобно бильярдным
шарам). Потенциальной энергией
взаимодействия молекул в модели
идеального газа пренебрегают.
Реальные газы (воздух) в обычных
земных условиях (Р~100кПа, Т~300K)
~действительно ведут себя подобно
идеальному газу.

3.

Уравнение состояния идеального газа
Уравнение состояния идеального газа: Р =
оно-же - уравнение Менделеева-Клапейрона:
nkT ,
РV = nkTV = νRT = (M/μ)RT
где R = kNA = 8,3 Дж/моль•К - универсальная газовая
постоянная; k = 1,38 х 10-23 Дж/К - постоянная Больцмана
Средняя кинетическая энергия поступательного движения
<Ek> = m<v2>/ 2 =3Θ / 2m = 3kT/2
Θ - термодинамическая температура (в Джоулях);
T = Θ/k - абсолютная температура, в градусах Кельвина [K]
молекул в газе:
Температура = мера средней кинетической энергии
движения молекул.
Среднеквадратичная скорость молекул (в атмосфере)
<v2>=3kT /m = 3RT/μ
=> v ~ 500 м/c

4.

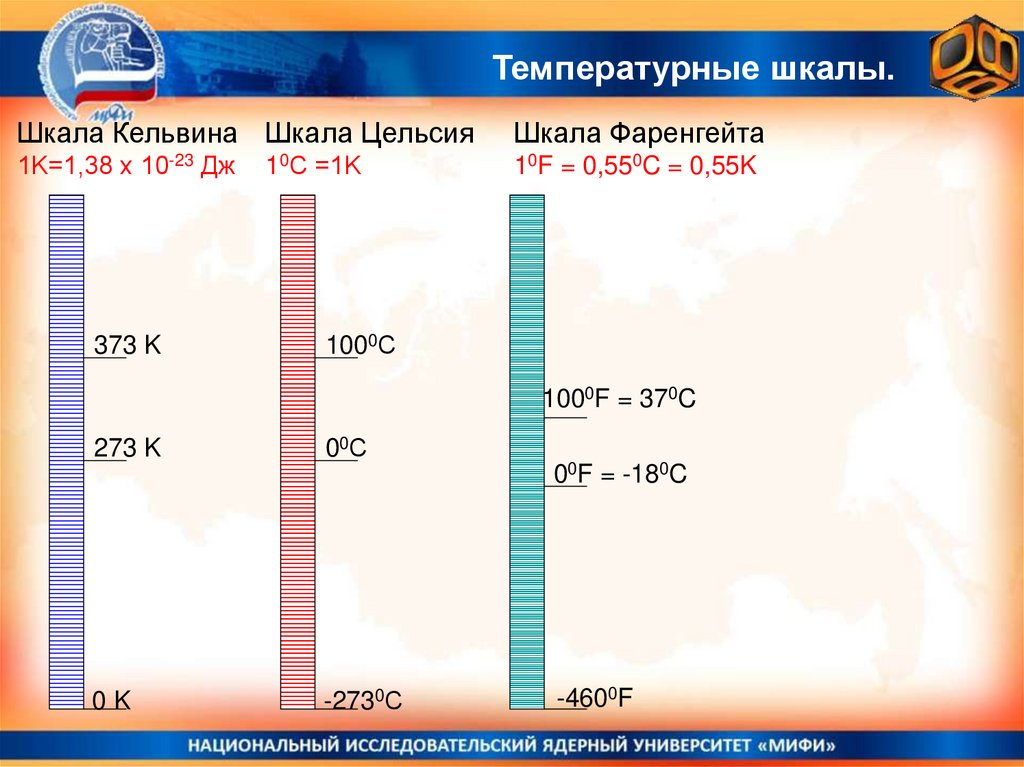
Температурные шкалы.
Шкала Кельвина Шкала Цельсия
Шкала Фаренгейта
1K=1,38 х 10-23 Дж
10F = 0,550C = 0,55K
373 K
10С =1K
1000С
1000F = 370C
273 K
00С
00F = -180C
0K
-2730С
-4600F

5.

СТЕПЕНИ СВОБОДЫ ДВИЖЕНИИЯ МОЛЕКУЛ
И
ТЕПЛОВАЯ (ВНУТРЕННЯЯ) ЭНЕРГИЯ ВЕЩЕСТВА
\

6.

Число степеней свободы многоатомной молекулы
Число степеней свободы – число независимых чисел (координат),
необходимое и достаточное для однозначного задания как положения
молекулы в пространстве, так и взаиморасположения ее атомов.
Положение центра масс молекулы определяют три координаты.
Движение центра масс = поступательное движение.
=> Молекула имеет три поступательных степени свободы.
Кинетическая энергия поступательного движения:
пост
ma y2
ma
m
ma z2
= (p,v)/2 = p2/2m
2
2
2
2
2
2
a x
Отдельные атомы имеют только 3 поступательные степени свободы

7.

Число степеней свободы многоатомной молекулы
Ориентацию молекулы в пространстве определяют
углы по отношению к 3-м осям координат.
Изменения этих углов - это вращательное движение.
=> в общем случае молекула может иметь три
вращательные степени свободы.
Кинетическая энергия вращательного движения
определяется соответствующими угловыми
скоростями ωx,y,z и моментами инерции Ix,y,z :
Eвращ = Ixωx2/2 + Iyωy2/2 + Izωz2/2 = (M,ω)/2
Жесткая многоатомная молекула (типа СН4, H2O, …)имеет шесть степеней
свободы: 3 поступательные + 3 вращательные. Её кинетическая энергия.
Екин = Eпост+Eвращ= (p, v)/2 + (M,ω)/2

8.

Число степеней свободы двух-атомной молекулы
Жесткая линейная молекула («гантель» - типа
N2, O2, СО2, …) – имеет только пять степеней
свободы: 3 поступательные и только две
вращательные
(Ix = Iy = I >> Iz ~> 0).
Ее кинетическая энергия равна:
Eкин = mv2/2 + Ixωx2/2 + Iyωy2/2 = mv2/2 + Iω2/2

9.

Число степеней свободы многоатомной молекулы
«Мягкая» упругая многоатомная молекула
Возможны
кпругие
смещения
атомов
друг
относительно
друга
=>
дополнительные
колебательные степени свободы.
Сколько колебательных степеней свободы может иметь молекула из N
атомов? Логика поиска ответа проста:
• N отдельных атомов имеют 3N степеней свободы.
• Соединившись в молекулу, они могут потерять часть своей свободы, но
никак не увеличить ее.
• => Общее число степеней свободы N-атомной молекулы не может превышать
3N.
Вычитая 3 поступательные и 2 или 3 вращательные степени, находим, что число
колебательных степеней свободы
• для линейных молекул не может быть больше, чем 3N - 5,
• для нелинейных – чем 3N -6.

10.

Число степеней свободы многоатомной молекулы
Число колебательных степеней свободы:
• для линейных молекул:
• для нелинейных молекул:
.
nкол < 3N-5
nкол < 3N-6
Энергия многоатомной молекулы (в гармоническом приближении
3
m j 2j
j 1
2
3(2)
j 1
k j j2 m j j2
2
2
j 1 2
I j 2j
nкол
j = 1, 2, 3 – соответственно x, y, z;
kj –коэффициенты упругости;
ξj – отклонения от положения равновесия.

11.

Число степеней свободы и способов накопления
энергии многоатомной молекулы
Молекула
Жесткая («холодная»)
Упругая («горячая»)
i = nпост+nвращ
i nпост nвращ 2nколеб
i 3пост 2вращ 5
i 3пост 3вращ 6
nколеб 3N 5
i < 6N - 5
nколеб 3N 6
i < 6(N – 1)

12.

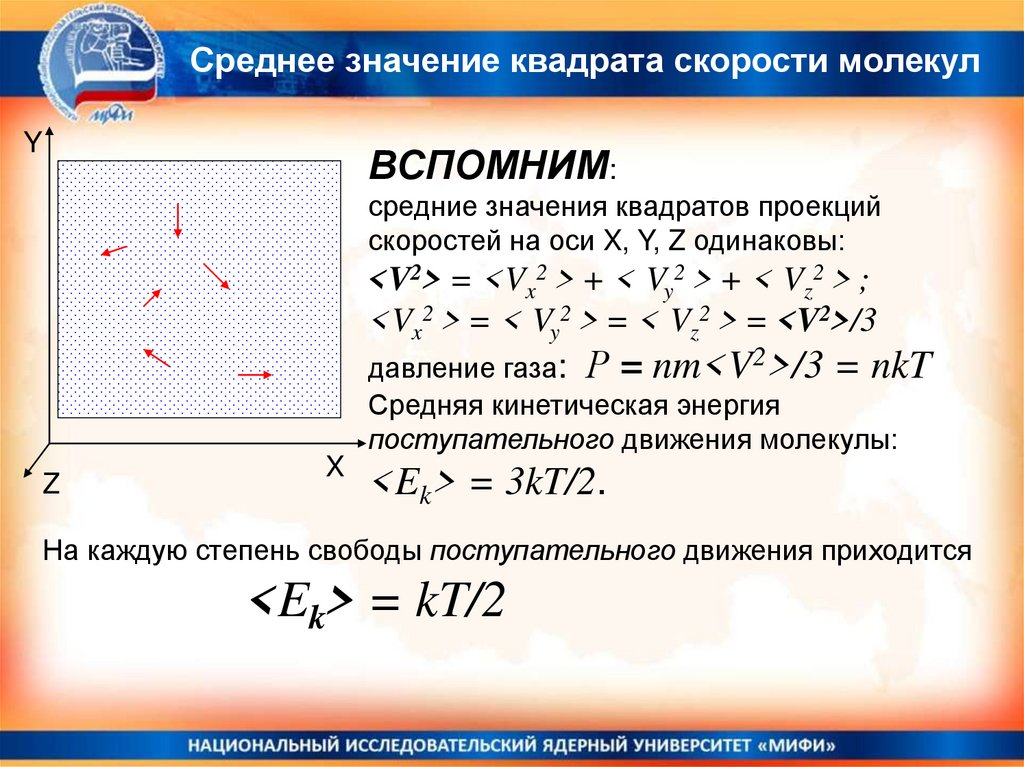
Среднее значение квадрата скорости молекул
Y
ВСПОМНИМ:
средние значения квадратов проекций
скоростей на оси X, Y, Z одинаковы:
<V2> = <Vx2 > + < Vy2 > + < Vz2 > ;
<Vx2 > = < Vy2 > = < Vz2 > = <V2>/3
давление газа: Р = nm<V2>/3 = nkT
Средняя кинетическая энергия
поступательного движения молекулы:
Z
X
<Ek> = 3kT/2.
На каждую степень свободы поступательного движения приходится
<Ek> = kT/2

13.

Равнораспределение энергии по степеням свободы
Основное допущение статистической термодинамики:
огромное число хаотических соударений и обменов энергией между
молекулами приводит к равномерному ее распределению по всем
возможным степеням свободы (способам накопления энергии)
причем на каждый способ приходится энергия, равная
Средняя энергия одной молекулы
kT/2
i
kT
2
i nпост nвращ 2nколеб
Колебательные степени свободы учитываются дважды, поскольку
колебательному движению соответствует как кинетическая,
так и потенциальная энергии

14.

Равнораспределение энергии по степеням свободы
На каждую «степень свободы» i приходится энергия kT/2
Средняя энергия одной молекулы:
i
kT
2
i nпост nвращ 2nколеб
При нормальных температурах колебательные степени свободы
«не задействованы»: i = 5 для 2-атомного газа, i
многоатомного, (i =3 для атомарного газа)
=6
для
Внутренняя энергия одного моля «идеального» газа равна
i
i
U м N A kN AT RT
2
2
Внутренняя энергия произвольного количества идеального газа:
U = ivRT/2

15.

Теплоемкость
Теплоёмкость
идеального газа

16.

Теплоемкость
Чтобы нагреть тело массы m от температуры Т1 до температуры Т1+dT
надо передать ему количество теплоты
dQ = СmdТ > 0
При охлаждении тело отдает то же количество теплоты (dQ < 0 ) .
С = dQ/dТ - теплоемкость тела, т.е. количество теплоты (Дж),
которое получает (или отдает) все тело при нагревании (или
охлаждении) на 1 К [C] = [ Дж/кг•К ]
с = dQ/mdТ - удельная теплоемкость вещества, т.е. количество
теплоты (Дж), которое получает (или отдает) 1 кг вещества при
нагревании (или охлаждении) на 1 К [C] = [ Дж/кг•К ]
сμ = dQ/vdT = μdQ/mdT = μс - молярная теплоемкость
вещества, т.е. количество теплоты (Дж), которое получает (отдает) 1
моль вещества при нагревании (охлаждении) на 1К. [Cμ] = [ Дж/моль•К ]

17.

Теплоемкость
сμ = dQ/vdT - молярная теплоемкость вещества, т.е. количество
теплоты, (Дж) которое получает (или отдает) 1 моль вещества при
нагревании (или охлаждении) на 1 К [Cμ] = [ Дж/моль•К ]
Uμ = iRT/2 - внутренняя энергия одного моля идеального газ
Если вся подводимая энергия идет только на увеличение внутренней
энергии газа – его молярная теплоемкость будет равна
cμ = dQ/vdT = iRdT/2dT = iR/2
Вся подводимая энергия идет только на увеличение внутренней
энергии газа, если объем его при нагревании не меняется.
Молярная теплоёмкость при постоянном объеме:
V
c = iR/2
ВОПРОС: а если НЕ ВСЯ подводимая энергия идет на увеличение
внутренней энергии газа? Что, если газ, расширяясь, ещё и совершает
механическую работу, также требующую затрат энергии?

18.

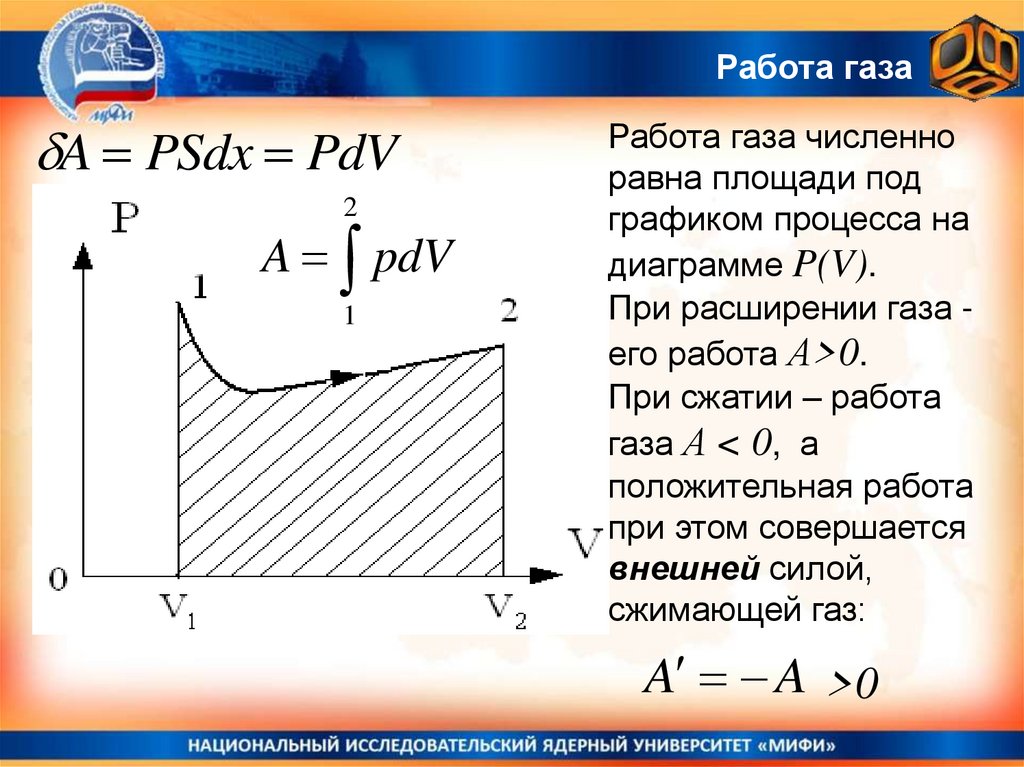
Термодинамика – работа газа
Газ давит на поршень с силой
F = PS и, при малом смещении
поршня dx, совершает работу
dA = PSdx = PdV
dV - приращение объема газа.
Эта формула справедлива для любой
формы сосуда с расширяющимся
газом.
,
Поршень равномерно и медленно перемещается в положительном
направлении оси X под действием ударов молекул (ma = 0)

19.

Работа газа
A PSdx PdV
2
A pdV
1
Работа газа численно
равна площади под
графиком процесса на
диаграмме P(V).
При расширении газа его работа А>0.
При сжатии – работа
газа А < 0, а
положительная работа
при этом совершается
внешней силой,
сжимающей газ:
A A >0

20.

Термодинамика – работа газа
A PSdx PdV
2
A pdV A A
1
P
dAi PdSi dxi PdVi
dA dAi P dSi dxi PdV
i
i

21.

Термодинамика – работа газа
Если газ совершает положительную работу (расширяется)
без подвода внешней энергии) - его внутренняя энергия (и
температура) уменьшаются.
dA = PdV>0 => dU < 0
Если внешние силы совершают над газом положительную
работу (сжимают газ) - эта работа идет на увеличение
внутренней энергии газа.
dAвнеш = -PdV > 0 => dU > 0

22.

Первое начало термодинамики
(закон сохранения энергии)
Изменение внутренней энергии системы U при переходе ее
из одного состояния в другое равно сумме работы внешних
сил Aвнеш и количества теплоты Q, переданного системе:
при её нвгревании (отнятого при охлаждении)
dU = dQ + dAвнеш ( = dQ - dAгаза)
Если система изолирована - т.е. над ней не совершается
работа и не происходит теплообмена с внешними телами её внутренняя энергия остается неизменной (сохраняется).
Энергия в природе не возникает из ничего и не исчезает.
Она только переходит из одной формы в другую.

23.

Теплоёмкость. Изопроцессы
dQ = dU + dAгаза = ivRdT/2 + PdV
cμ = dQ/vdT = iR/2 + PdV/vdT;
УМК: PV = vRT =>
Изотермический процесс: T=const.; dU = 0; dQ = PdV = 0
cμT = dQ/vdT = ∞
Изохорный процесс: V = const.; dA = 0; dU = dQ
/
cμV = dU/vdT = iR/2
Изобарный процесс: P = const.; dA = PdV = vRdT
cμP = iR/2 +R = (i+2)R/2
Адиабатный процесс: dQ = 0 (теплоизолированная система)
cμQ = dQ/vdT = 0
C
i 2 показатель
P
CV
i адиабаты

24.

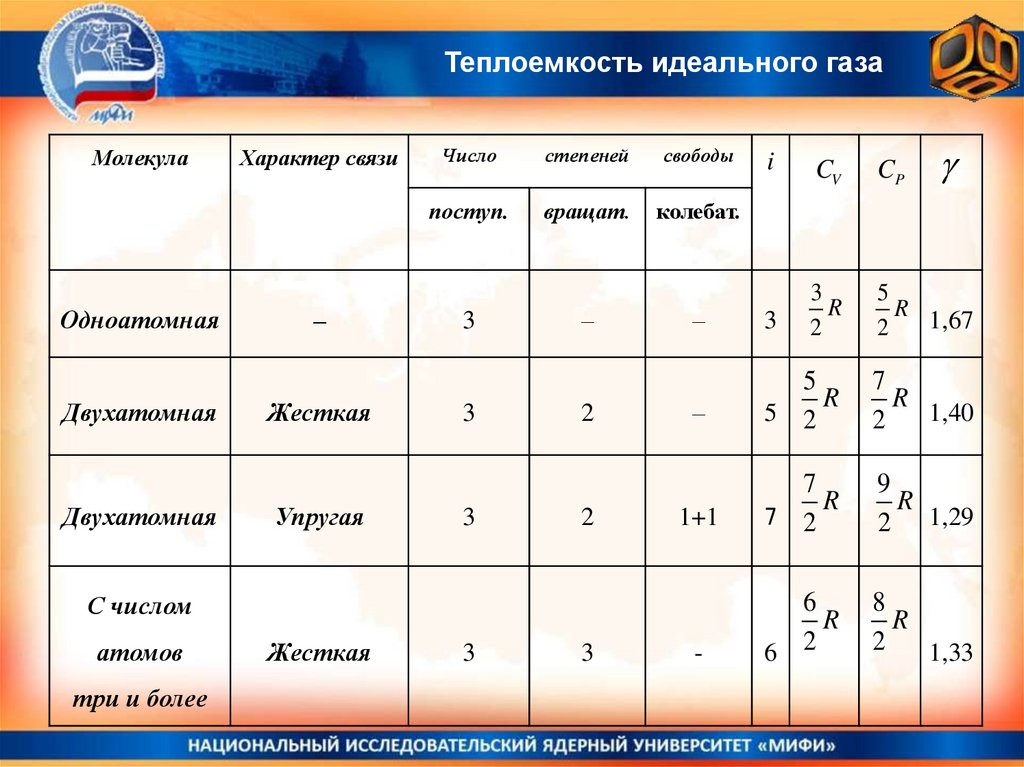
Теплоемкость идеального газа
Молекула
Одноатомная
Двухатомная
Двухатомная
Характер связи
–
Жесткая
Упругая
Число
степеней
свободы
поступ.
вращат.
колебат.
3
3
3
–
2
2
CV
CP
–
3
3
R
2
5
R
1,67
2
–
5
R
5 2
7
R
1,40
2
1+1
7
R
7 2
9
R
2 1,29
-
6
R
6 2
8
R
2
1,33
С числом
атомов
три и более
Жесткая
3
3
i

25.

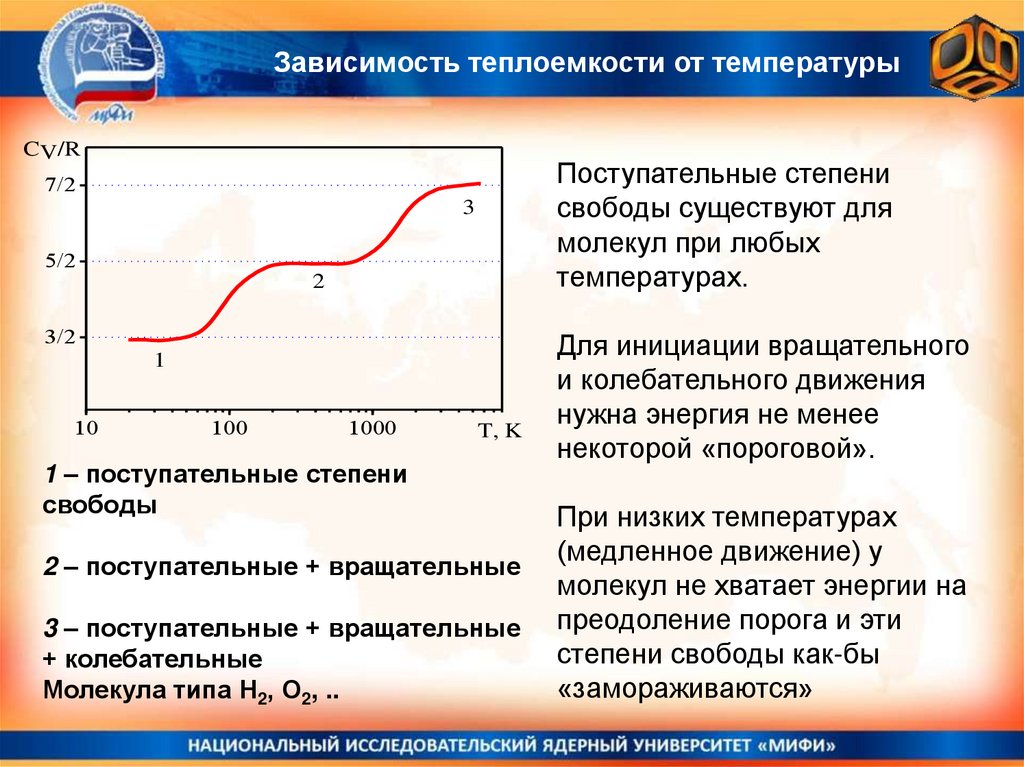
Зависимость теплоемкости от температуры
CV/R
Поступательные степени
свободы существуют для
молекул при любых
температурах.
7/2
3
5/2
2
3/2
1
10
100
1000
T, K
1 – поступательные степени
свободы
2 – поступательные + вращательные
3 – поступательные + вращательные
+ колебательные
Молекула типа Н2, О2, ..
Для инициации вращательного
и колебательного движения
нужна энергия не менее
некоторой «пороговой».
При низких температурах
(медленное движение) у
молекул не хватает энергии на
преодоление порога и эти
степени свободы как-бы
«замораживаются»

26.

Подведем первые итоги:
Основное уравнение состояния идеального газа:
Р = nkT
Уравнение Менделеева-Клапейрона:
РV = νRT = (M/μ)RT
Внутренняя энергия газа:
U = iνRT/2
I-ое Начало Термодинамики (закон сохранения энергии):
dQ = dU + dAгаза= iνRdT/2 + PdV

27.

Курс общей физики НИЯУ МИФИ
Основы молекулярной и статистической
физики
Лекция 03 (06)
Термодинамика. Теплоёмкость.
Спасибо за внимание!