Призма

1.

Термин «призма» греческого происхождения и
буквально означает «отпиленное» бревно.

2.

Тема урока: ПРИЗМА
Цели урока:
а) построить определение: призмы; элементов
призмы;
б) узнать виды призм;
в) вывести формулы для вычисления площадей
полной и боковой поверхностей призмы

3.

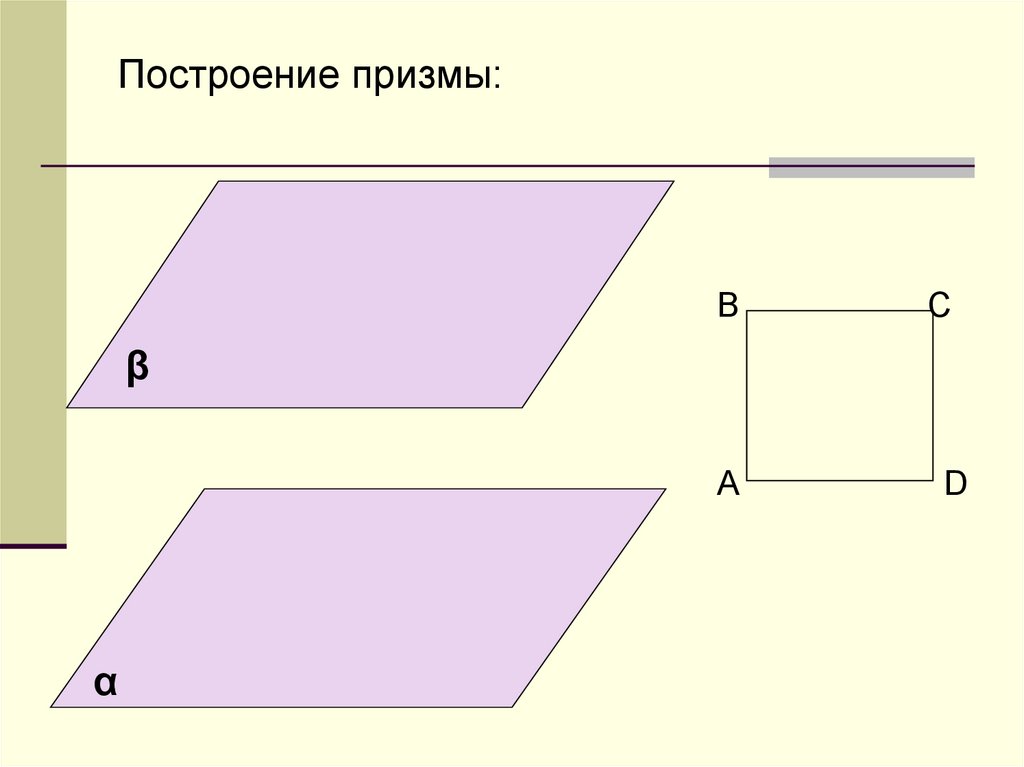
Построение призмы:
B
C
β
А
α
D

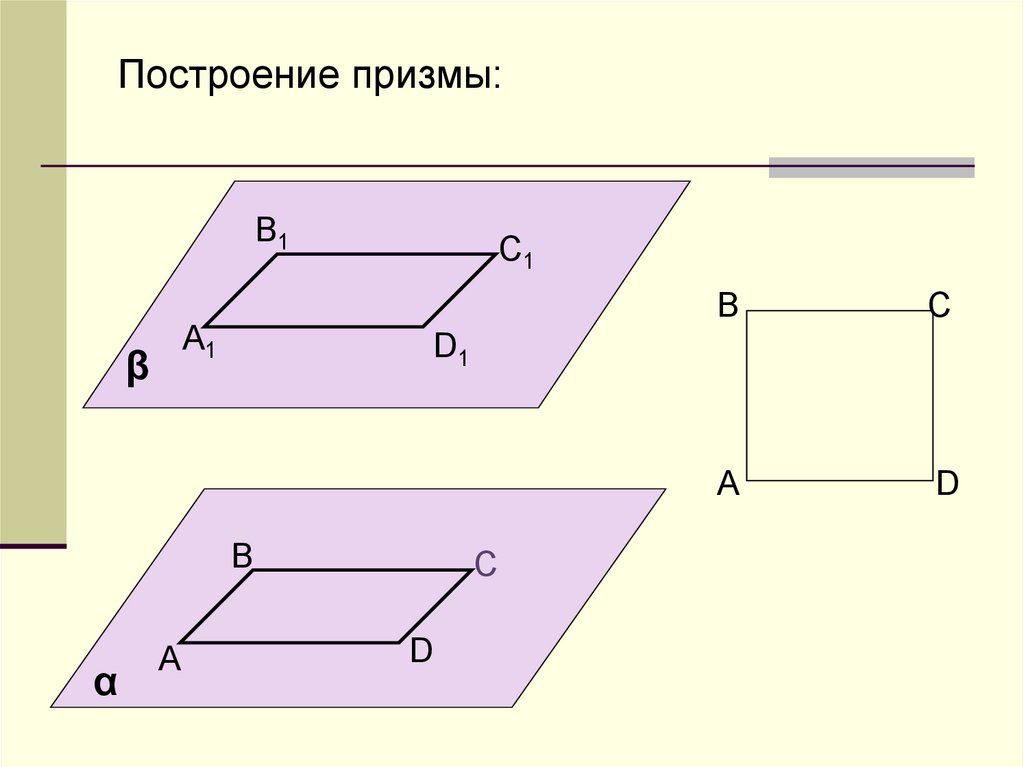
4.

Построение призмы:
B1
А1
β
C1
α
C
А
D
D1
B
А
B
C
D

5.

Построение призмы:
B1
А1
β
C1
α
C
А
D
D1
B
А
B
C
D

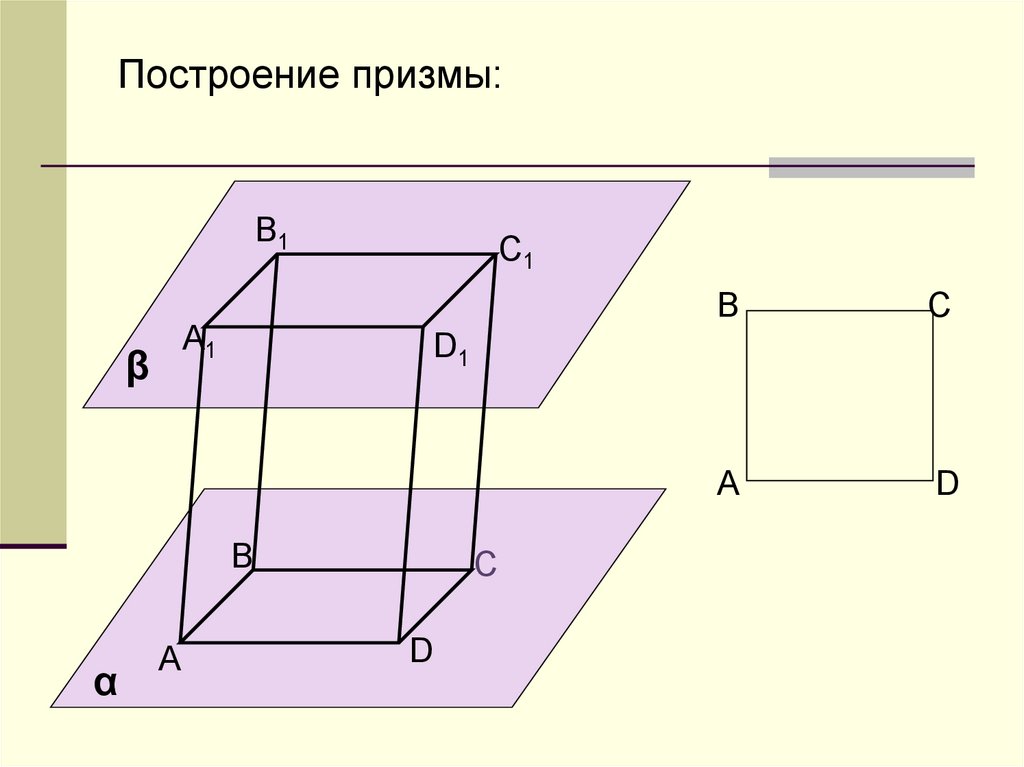
6.

Построение призмы:
B1
А1
β
C1
α
C
А
D
D1
B
А
B
C
D

7.

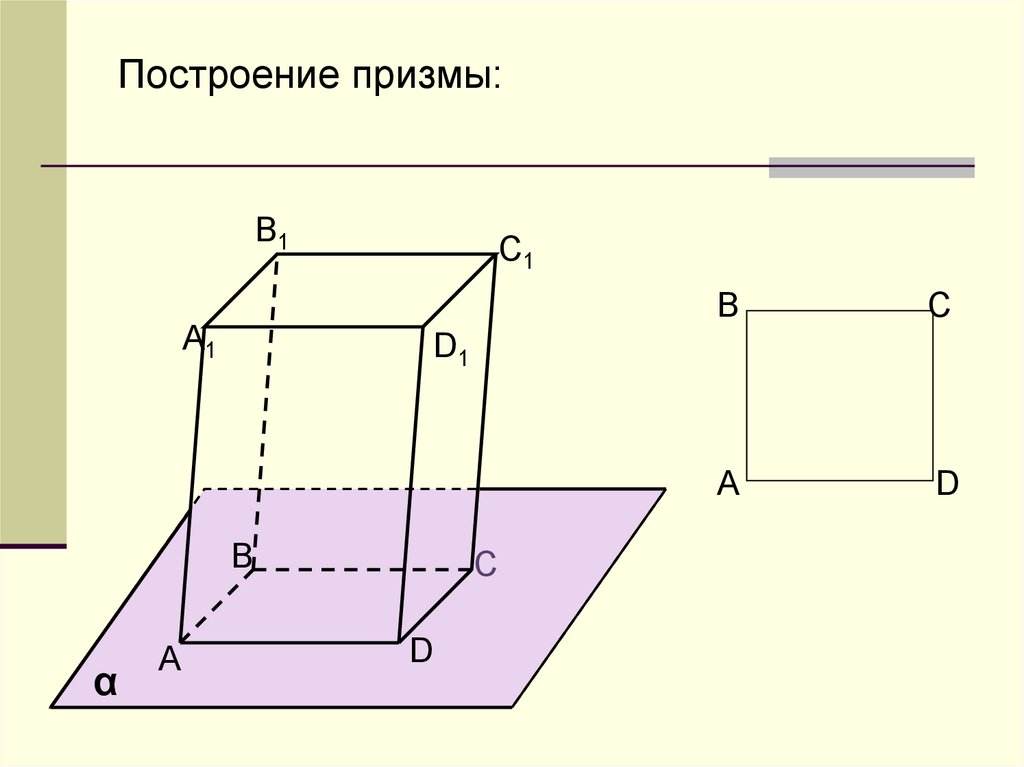
Построение призмы:
B1
А1
C1
α
C
А
D
D1
B
А
B
C
D

8.

Элементы призмы:
N
1.
ABCD, A1B1C1D1 – основания;
2.
AA1,BB1,CC1,DD1 – боковые ребра;
3.
AA1B1В, ВВ1С1С,СС1D1D,DD1A1A –
боковые грани;
4.
A,B,C,D, A1,B1,C1,D1 – вершинами;
5.
АС1, ВD1, A1C, B1D – диагонали;
6.
D1N –высота.
Совокупность всех боковых граней есть
боковая поверхность.
Совокупность всех граней есть полная
поверхность.

9.

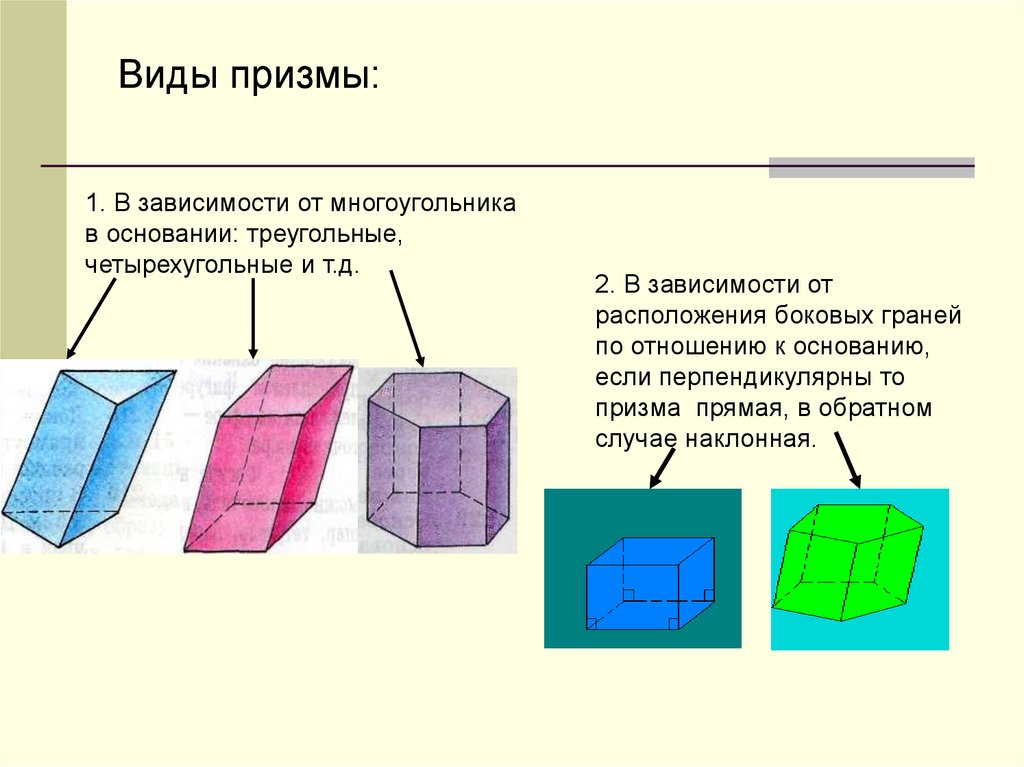
Виды призмы:
1. В зависимости от многоугольника
в основании: треугольные,
четырехугольные и т.д.
2. В зависимости от
расположения боковых граней
по отношению к основанию,
если перпендикулярны то
призма прямая, в обратном
случае наклонная.

10. Задание 1: Постройте прямую треугольную призму и отметьте все ее элементы

11.

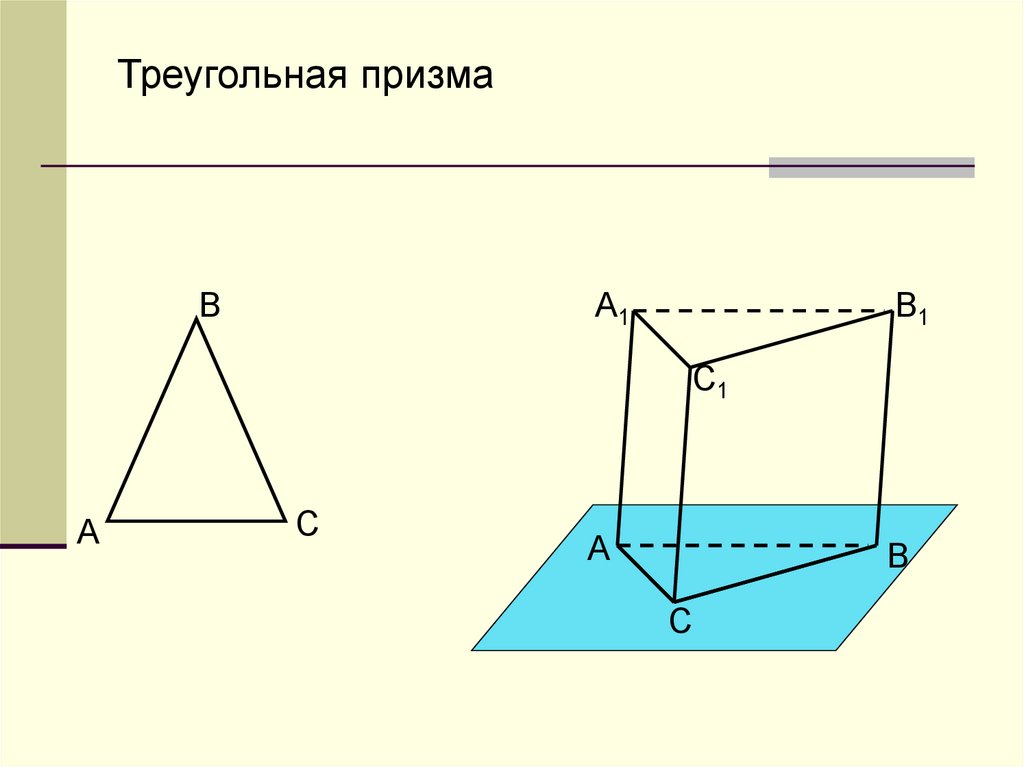
Треугольная призма
А1
B
B1
C1
А
C
А
B
C

12.

Прямая призма называется правильной, если ее
основания - правильные многоугольники. У такой
призмы все боковые грани – равные прямоугольники.

13.

Теорема: Площадь полной поверхности призмы равна сумме боковой
поверхности и двум площадям основания:
п. п.
б . п.
осн
S
S
2S
Доказательство:
Sосн
h
S1
h S2
а
b
h
b
h S3
Sосн
а
Sп.п.=S1+S2+S3+S4+Sосн.+Sосн.= Sб.п.+2Sосн
. Sб.п=a∙h+b∙h+a∙h+b∙h=h∙(a+b+a+b)=h∙Pосн.
Sп.п.= Sб.п.+2Sосн
а
Sб.п=h∙Pосн.
hS
4
b

14.

Задание 2. На столах модели призм. Измерить их элементы линейкой и
заполнить таблицу:
Элементы:
a
b
h
Pосн.
Sосн.
Sб.п.
Sп.п.
Модель №1
Модель №2

15.

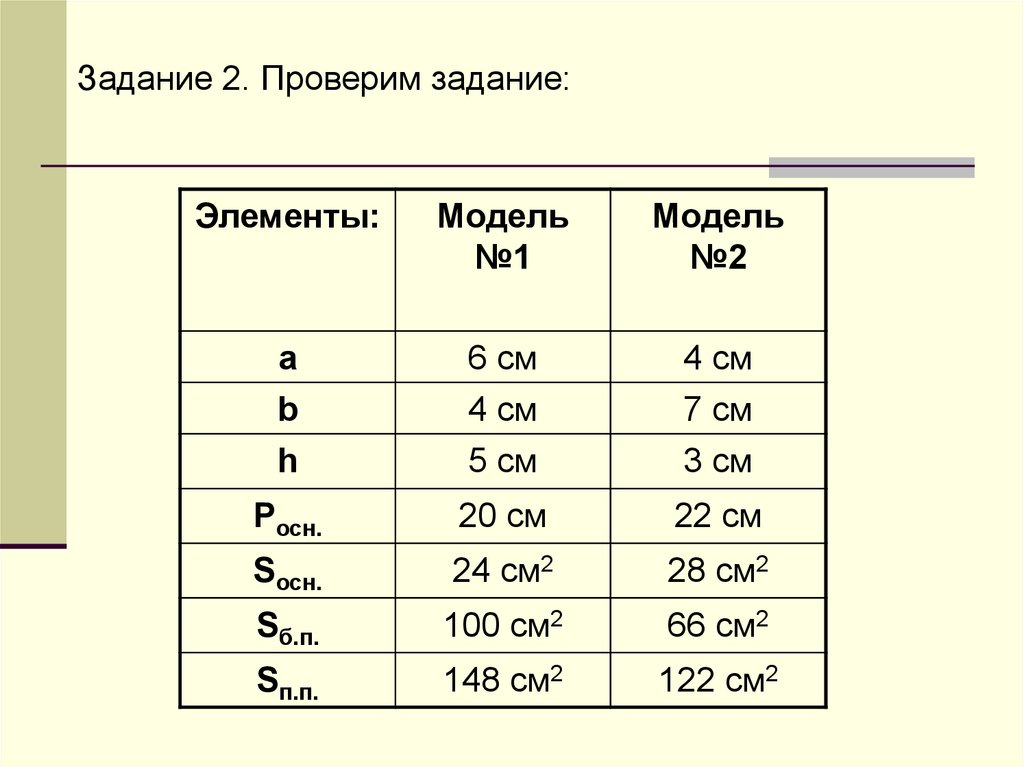
Задание 2. Проверим задание:
Элементы:
Модель
№1
Модель
№2
a
b
h
6 см
4 см
5 см
4 см
7 см
3 см
Pосн.
20 см
22 см
Sосн.
24 см2
28 см2
Sб.п.
100 см2
66 см2
Sп.п.
148 см2
122 см2

16.

1. Что нового вы узнали на уроке?
2. Что использовали для «открытия»
новых знаний?
3. Вы достигли поставленной цели?
4. Как вы оцените свою работу на уроке?

17. Домашнее задание: модель призмы; выписать все формулы для вычисления площадей различных треугольников, четырехугольников.

18.

Всем спасибо. Молодцы!