Similar presentations:
Призма. Виды призм
1.
ИзумрудсотыПчелиные
2.
Решётка магнияРешётка железа
3.
АквариумБашня Смоленской крепости
4.
ОбелискБеседка
5.
Призма6.
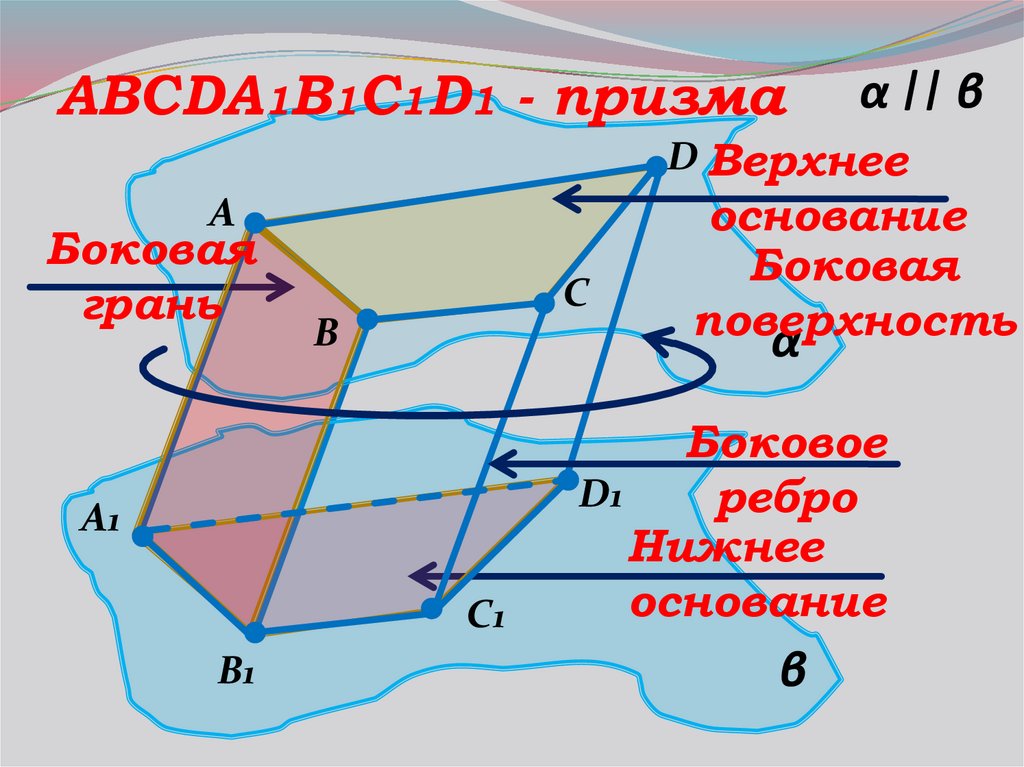
ABCDA1B1C1D1 - призмаα || β
D Верхнее
A
Боковая
грань
C
B
A1
C1
B1
основание
Боковая
поверхность
α
Боковое
D1
ребро
Нижнее
основание
β
7.
Виды призмD
A
C
B
D1
A1
C1
B1
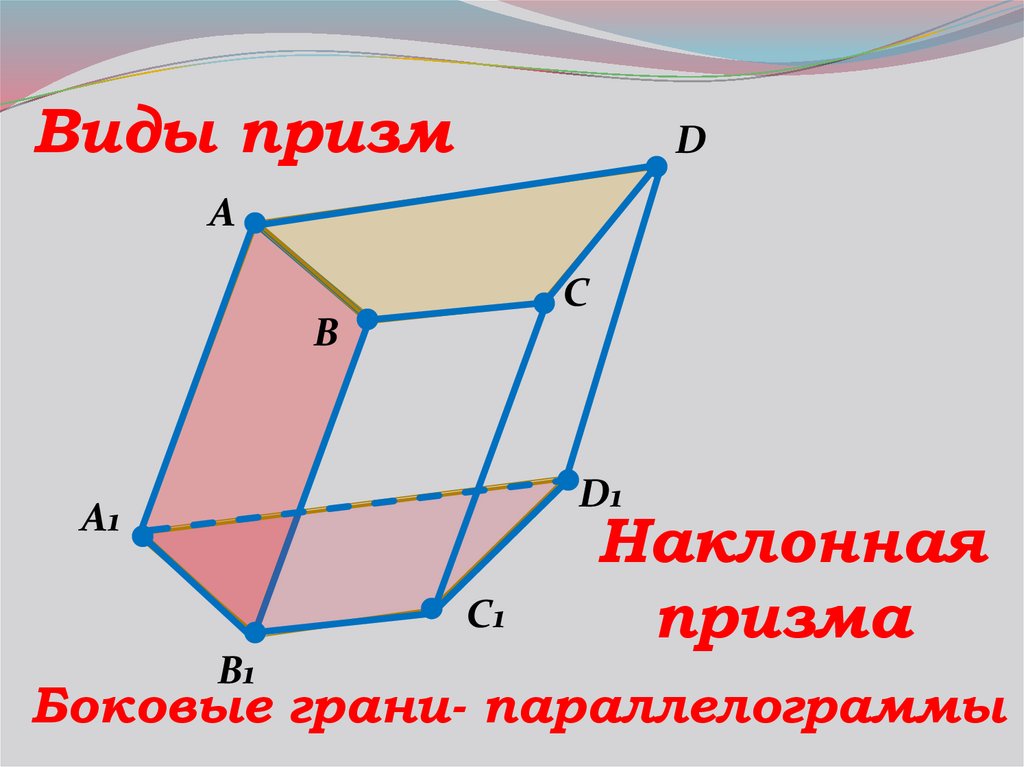
Наклонная
призма
Боковые грани- параллелограммы
8.
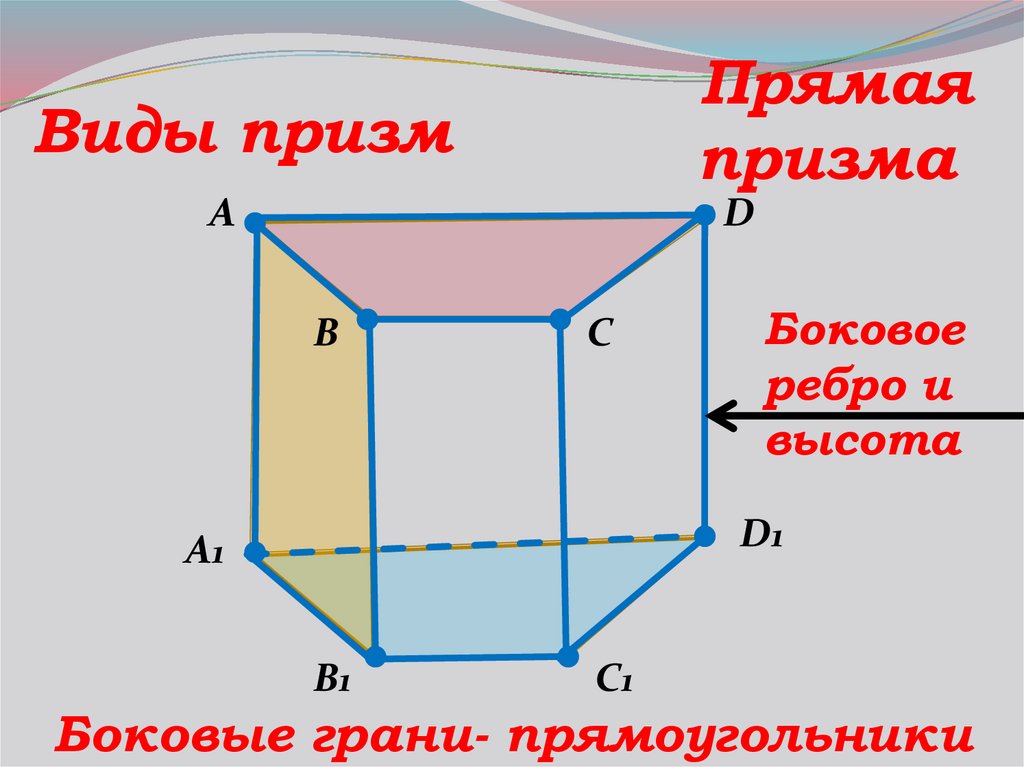
Прямаяпризма
Виды призм
A
D
B
C
Боковое
ребро и
высота
D1
A1
B1
C1
Боковые грани- прямоугольники
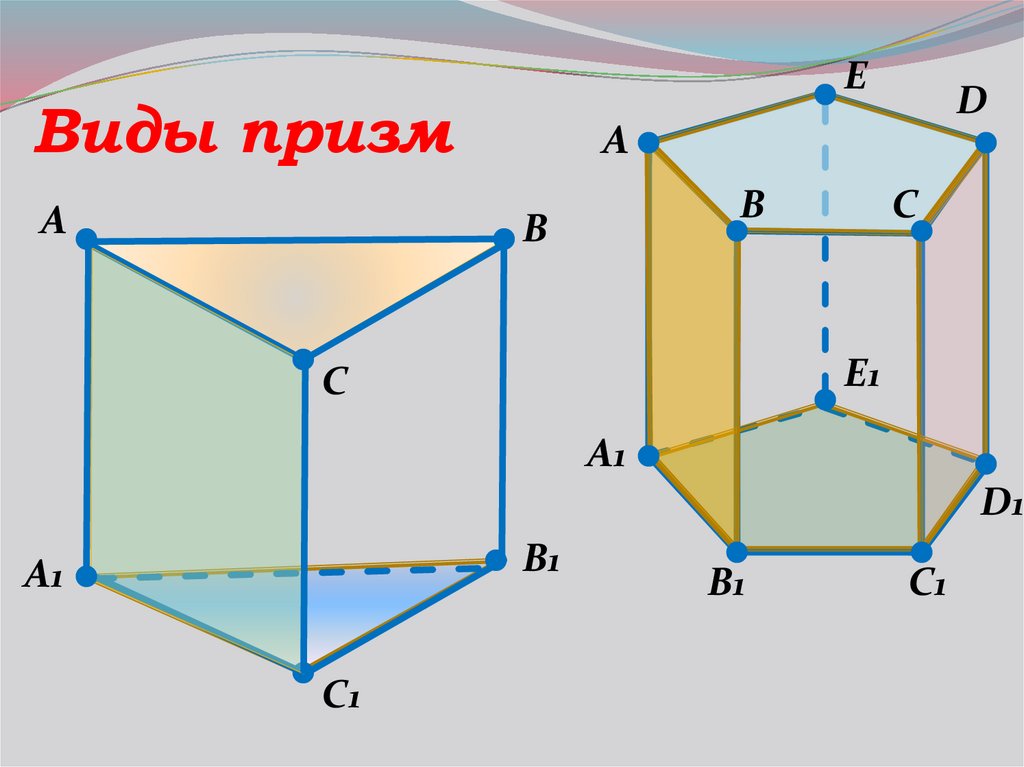
9.
EВиды призм
A
D
A
B
B
C
E1
C
A1
D1
B1
A1
C1
B1
C1
10.
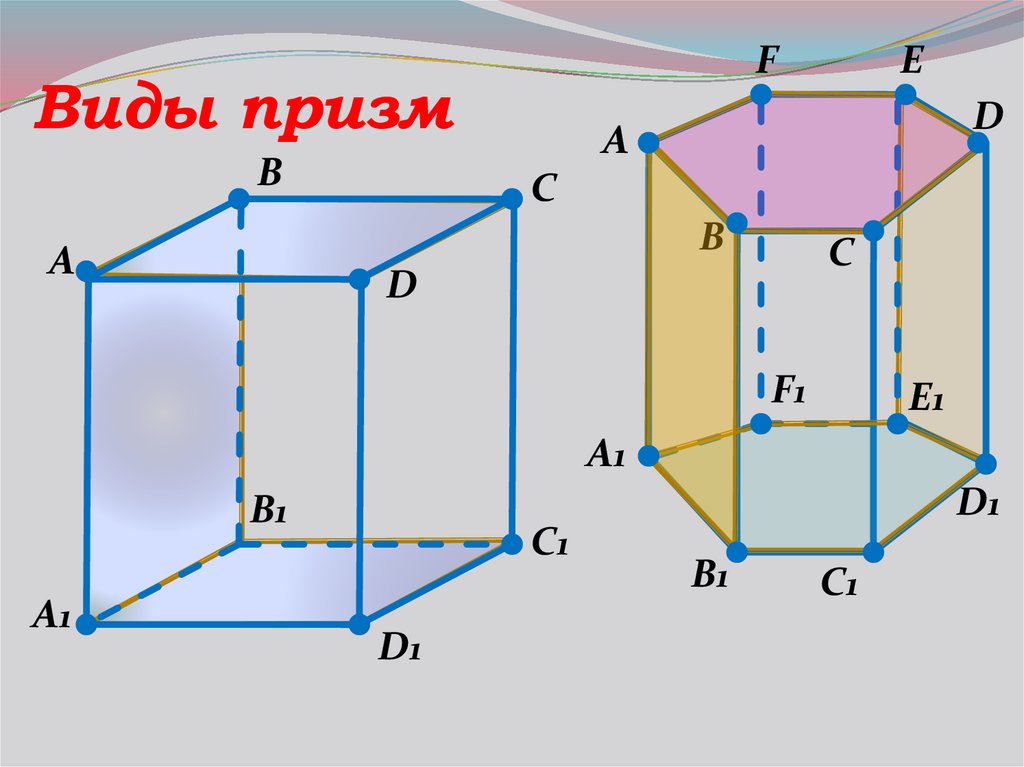
FВиды призм
B
D
A
C
B
A
E
C
D
F1
E1
A1
D1
B1
A1
C1
D1
B1
C1
11. Прямая призма называется правильной, если её основания - правильные многоугольники
Прямая призма называетсяправильной, если её основания правильные многоугольники
C1
D1
B1
A1
C
D
A
B
12.
Площадь боковой поверхности прямойпризмы равна произведению периметра
основания на высоту призмы
B1
Sбок.п.= SАВВ1А1+ SBCC1B1+
C1
А1
+SCDD1C1…=
=АВ·ВВ1+ВС·ВВ1+CD·BB1=
D1
E1
=ВВ1·(АВ+ВС+СD+…)=
B
=Pосн.·h
А
C
D
E
Sпол.пов.=Sбок.пов.+ 2Sосн.
13.
Презентацию подготовилаДудоладова М.П.
Учитель математики.
Использовать на уроке
открытия нового знания.








 mathematics
mathematics








