Параллелепипед и куб

1. Открытый урок по геометрии

Параллелепипед и куб
Подготовили преподаватели ГОУ
НПО ПЛ №18 г. Кирова
• Маковеева Елена Николаевна
• Печенкина Наталья Николаевна

2.

3. Цели урока:

• Повторить
этапы
построения
геометрических
тел
средствами ПК; продолжить формирование навыков работы
с векторным графическим редактором; продолжить
формирование навыка работы с электронными тестами, с
гипертекстовыми документами.
• Развить и конкретизировать знания о прямоугольном
параллелепипеде и кубе – используя свойства тел при их
вычерчивании на ПК;
• Продолжить формирование навыка работы с обучающими
программами;
• Продолжить развитие внимания, памяти, взаимопомощи,
логического мышления, самостоятельности;
• Воспитание
интереса
к
знаниям
по
настойчивости, упорства в достижении цели.
предметам,

4.

Примеры параллелепипедов, которые можно
найти в окружающем мире
Высотное здание на
площади Восстания
Архангельское,
санаторий

5.

Знаменитый Биг Бен

6.

Ново –
Иерусалимский храм

7.

Прямоугольный параллелепипед
D1
C1
A1
A1B1C1D1
B1
b
D
ABCD
AA1D1D
c
C
a
A
AA1B1B=DD1C1C
ADD1A1=BCC1B1
ABCD=A1B1C1D1
B
BB1C1C
AA1B1B
DD1C1C
Прямоугольники

8.

Прямоугольный параллелепипед
D1
C1
A1
BB11
b
D
AA1B1B
c
C
Прямоугольники
DD1C1C
a
A
B
AA1B1B=DD1C1C

9. Противоположные ребра прямоугольного параллелепипеда равны

AA1=BB1=CC1=DD1
C1
B1
D1
A1
B
AA1+BB1+CC1+DD1+AB+A1B1+
+CD+C1D1+AD+A1D1+BC+B1C1=
C
A
AD=A1D1=BC=B1C1
AB=A1B1=CD=C1D1
D
=4*(BB1+AB+BC)=
=4*(AA1+AB+AD)=
=4*(DD1+ DC+DA)=
=4*(CC1 +CD +CB)

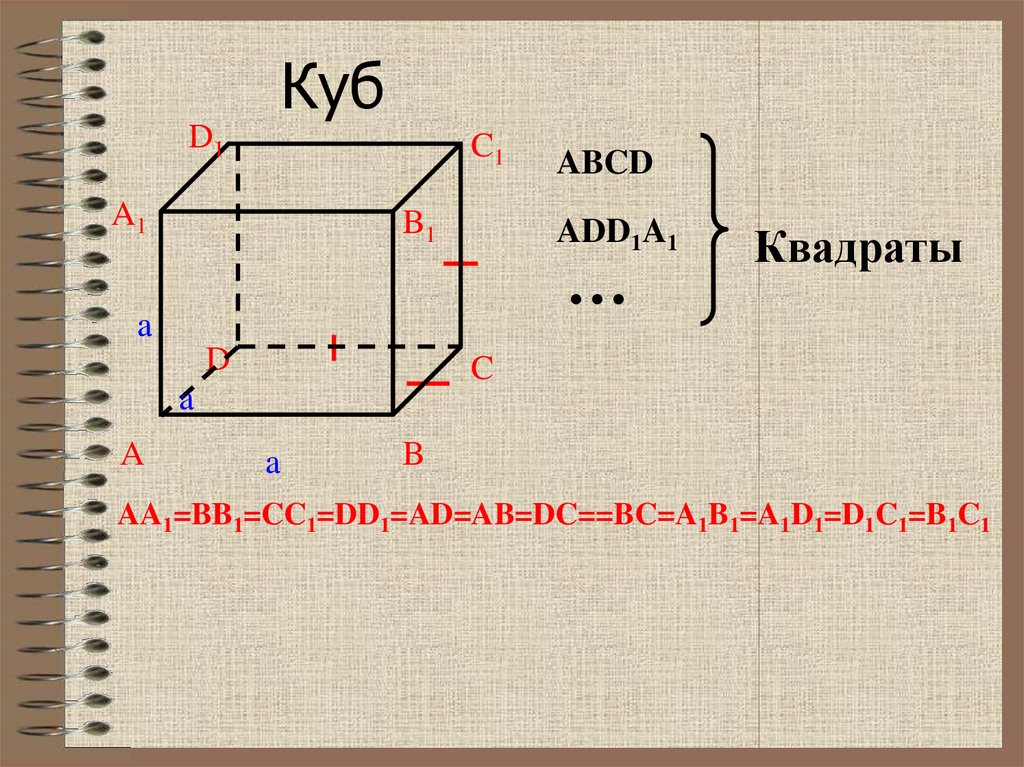
10.

Куб
D1
C1
A1
B1
ADD1A1
…
a
D
Квадраты
C
a
A
ABCD
a
B
AA1=BB1=CC1=DD1=AD=AB=DC==BC=A1B1=A1D1=D1C1=B1C1

11. Площадь боковой поверхности Sбоковой поверхности

D1
c a
A
A1
D1
A1
C1
B1
B1
C1
a
D
C
b
B
D
a
a
A
B
Sбп=4• a2
Sбп=2 •(bc+ac)
C

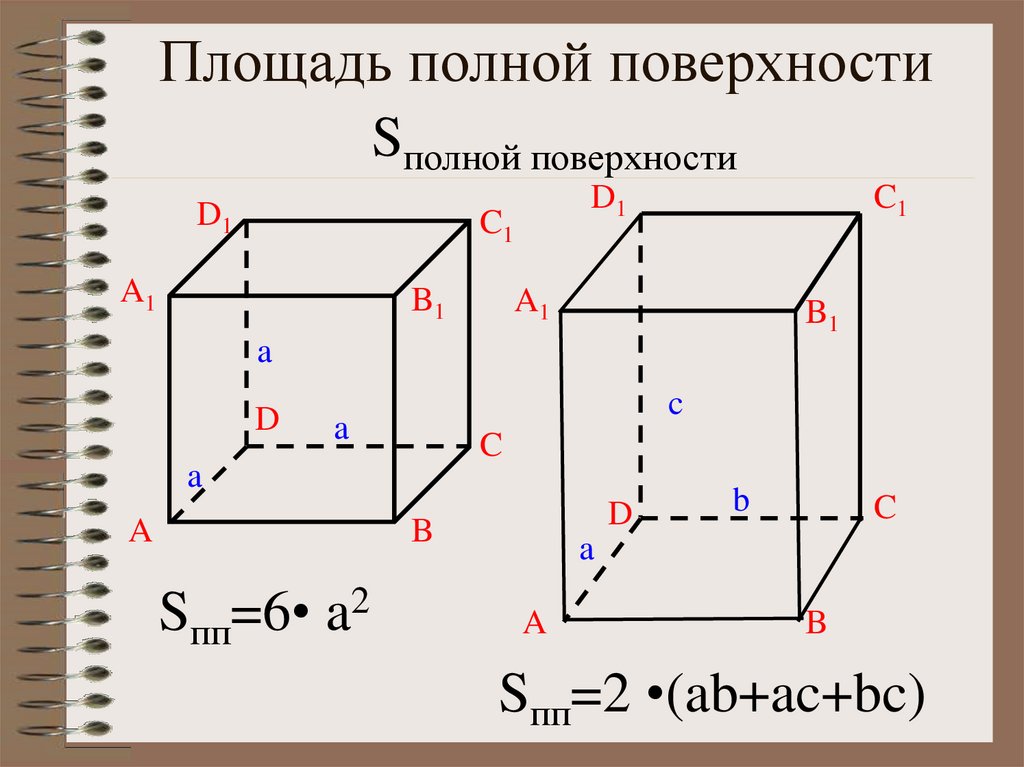
12. Площадь полной поверхности Sполной поверхности

D1
D1
C1
A1
B1
C1
A1
B1
a
D
c
a
C
a
A
D
B
Sпп=6• a2
b
C
a
A
B
Sпп=2 •(ab+ac+bc)

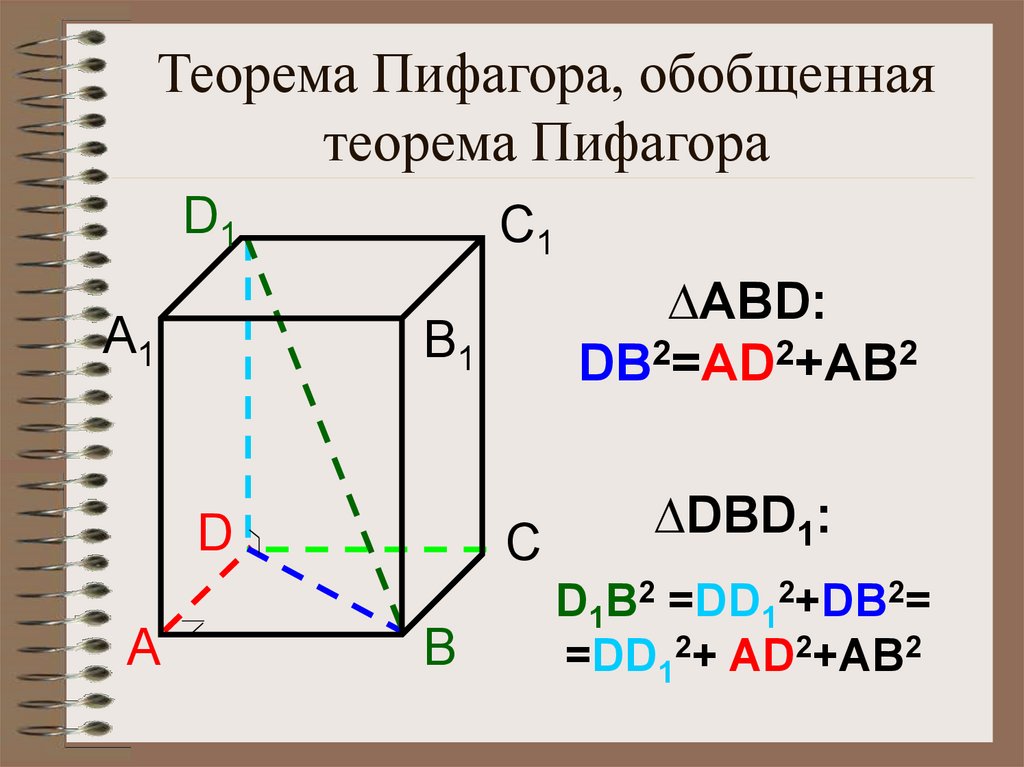
13. Теорема Пифагора, обобщенная теорема Пифагора

D1
А1
C1
B1
D
А
∆ABD:
DB2=AD2+AB2
C
B
∆DBD1:
D1B2 =DD12+DB2=
=DD12+ AD2+AB2

14. Домашнее задание: Построить проект офисного здания. Готовые образцы объемных фигур находятся в файле материалы для

строительства.