Similar presentations:
Задачи на построение сечений тетраэдра и параллелепипеда (10 класс)
1. Задачи на построение сечений тетраэдра и параллелепипеда
Геометрия, 10 класс2. Понятие сечения
Секущая плоскость тетраэдра(параллелепипеда) любая плоскость, по
обе стороны от которой имеются точки
данного тетраэдра (параллелепипеда).
Секущая плоскость пересекает грани
тетраэдра (параллелепипеда) по
отрезкам. Многоугольник, сторонами
которого являются эти отрезки,
называется сечением тетраэдра
(параллелепипеда).
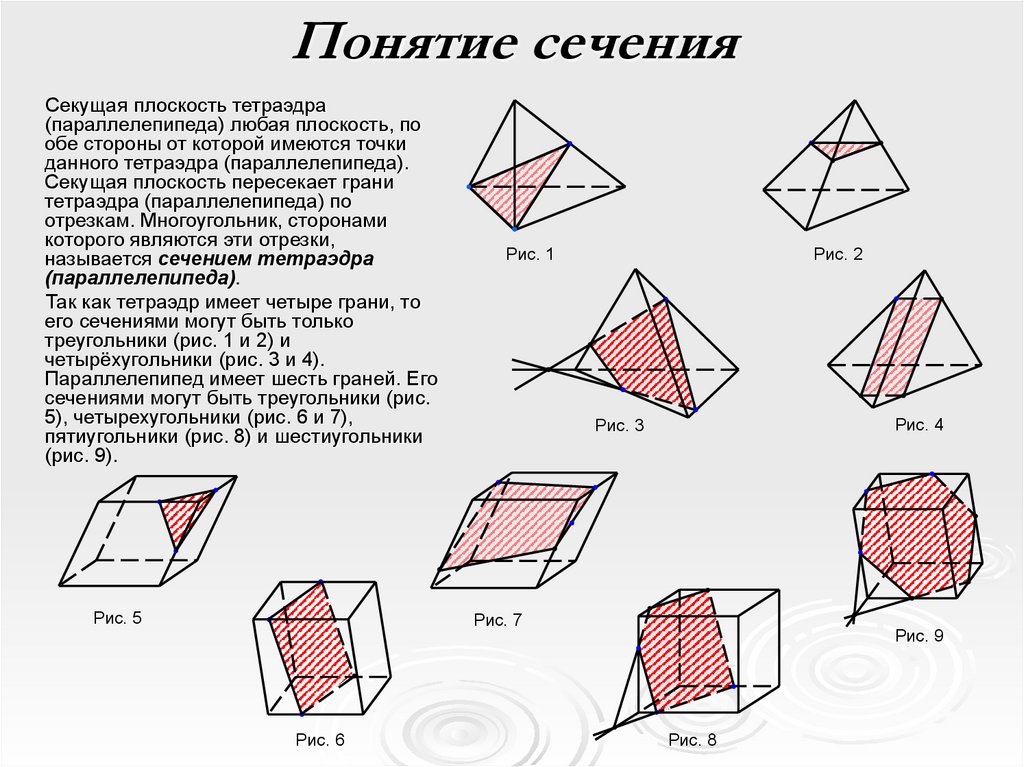
Так как тетраэдр имеет четыре грани, то
его сечениями могут быть только
треугольники (рис. 1 и 2) и
четырёхугольники (рис. 3 и 4).
Параллелепипед имеет шесть граней. Его
сечениями могут быть треугольники (рис.
5), четырехугольники (рис. 6 и 7),
пятиугольники (рис. 8) и шестиугольники
(рис. 9).
Рис. 5
Рис. 1
Рис. 2
Рис. 4
Рис. 3
Рис. 7
Рис. 6
Рис. 9
Рис. 8
3.
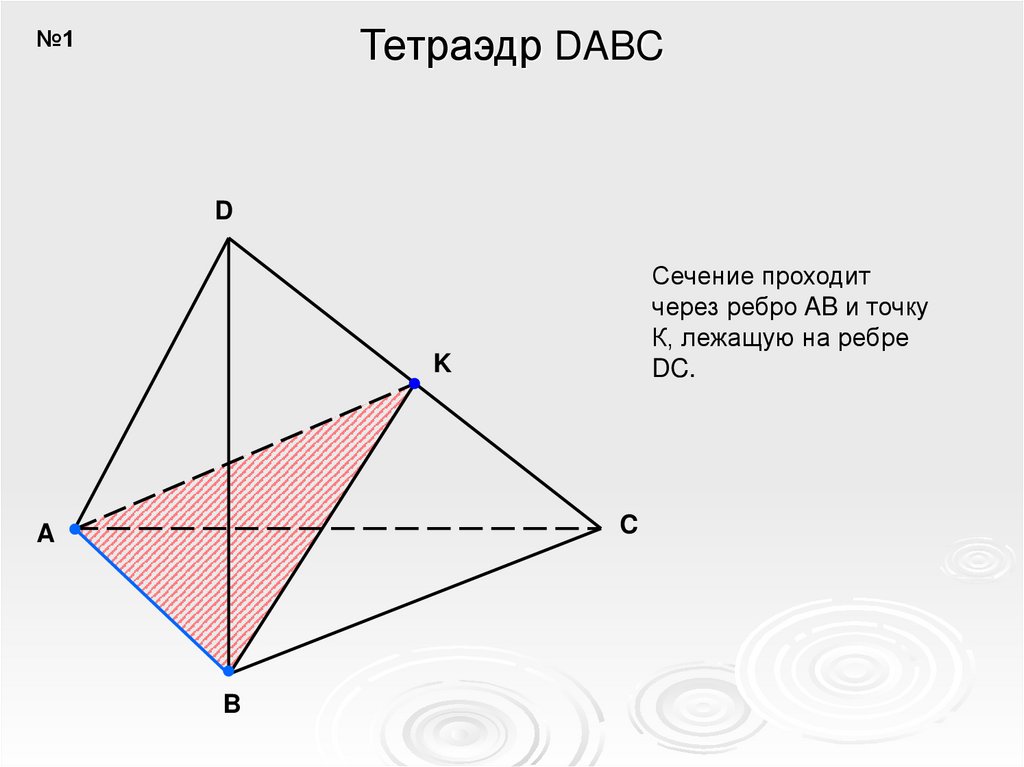
Тетраэдр DABC№1
D
Сечение проходит
через ребро AB и точку
К, лежащую на ребре
DC.
K
C
A
B
4.
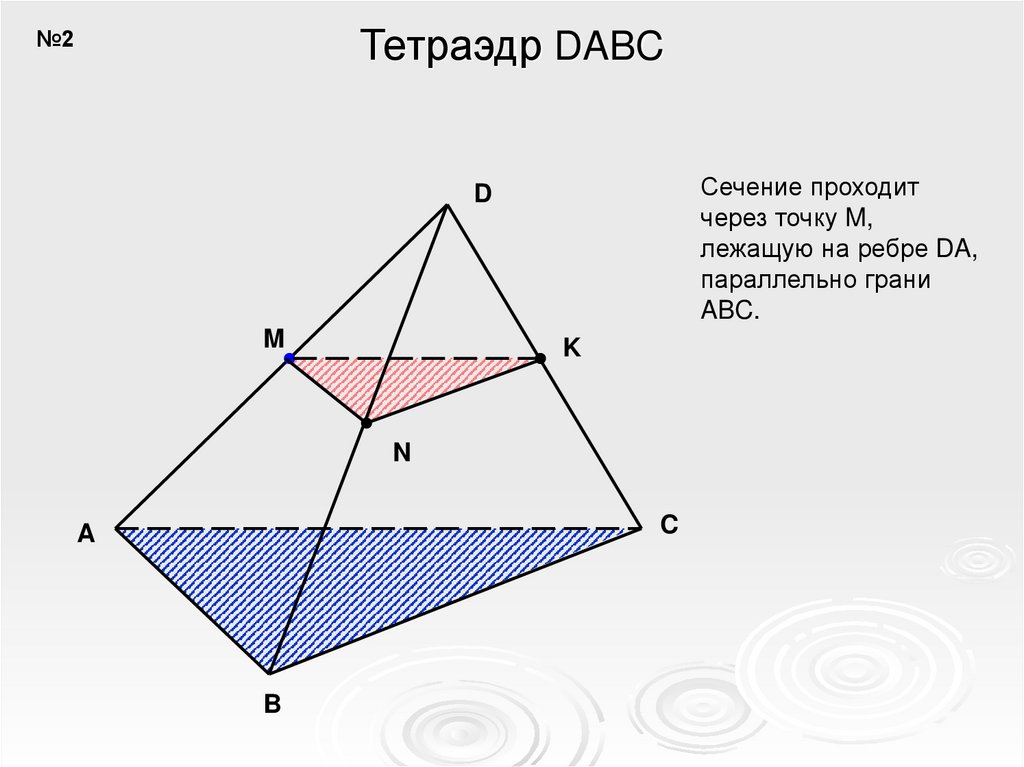
Тетраэдр DABC№2
Сечение проходит
через точку M,
лежащую на ребре DA,
параллельно грани
ABC.
D
M
K
N
C
A
B
5.
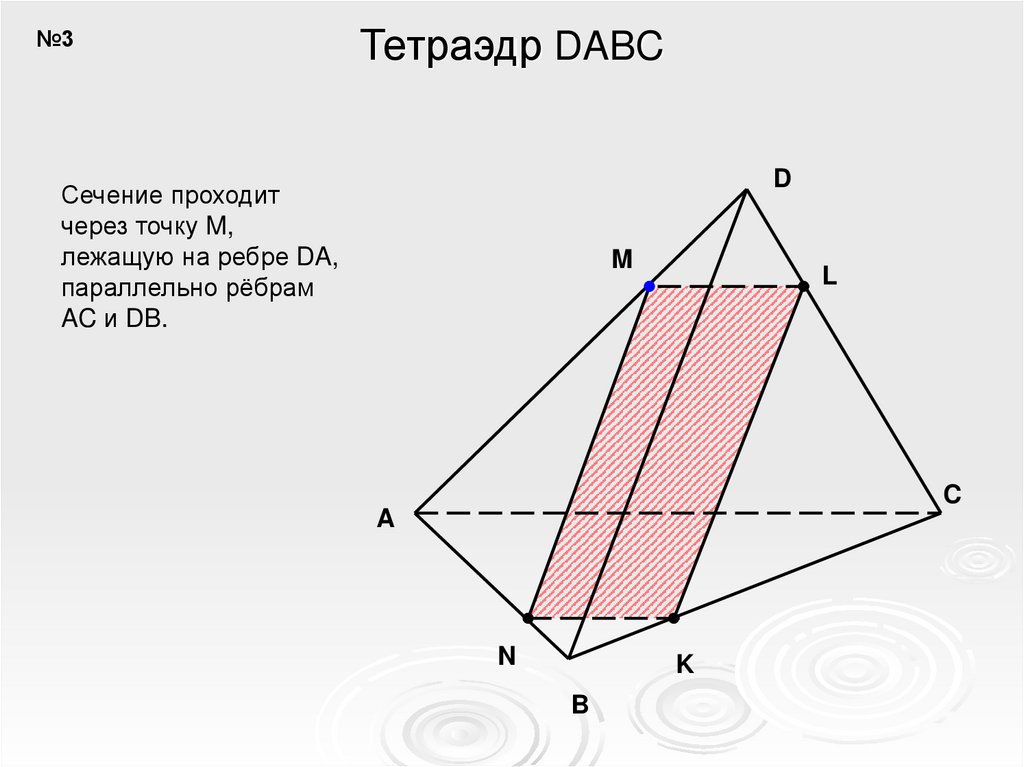
№3Тетраэдр DABC
D
Сечение проходит
через точку M,
лежащую на ребре DA,
параллельно рёбрам
AC и DB.
M
L
C
A
N
K
B
6.
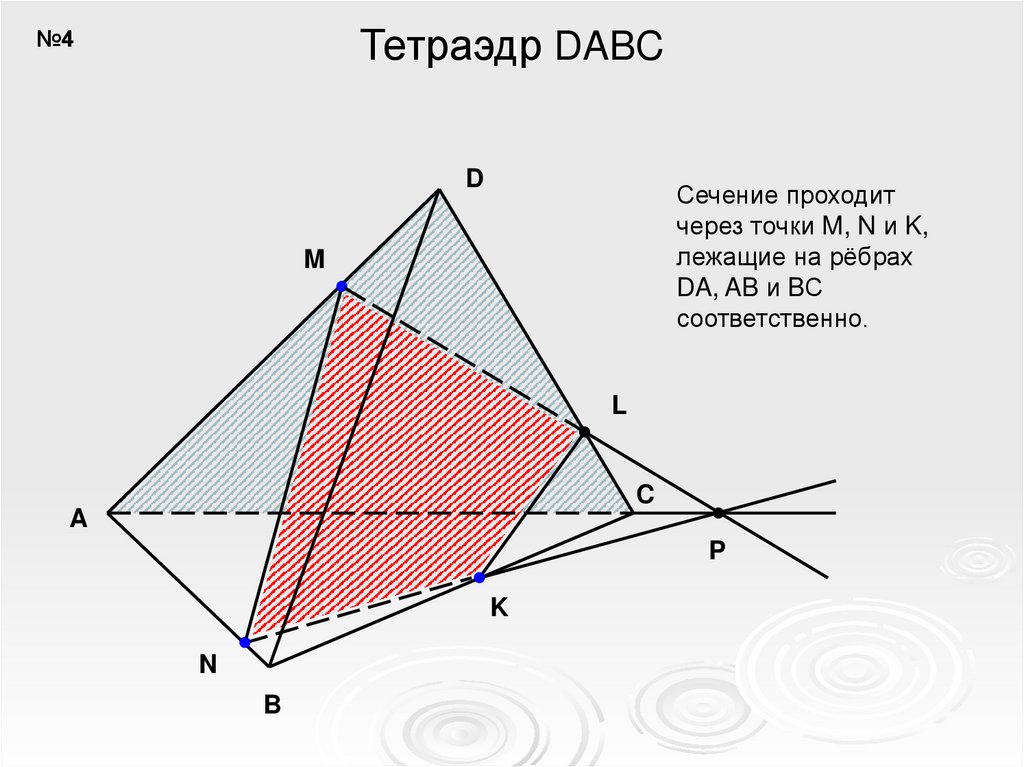
Тетраэдр DABC№4
D
Сечение проходит
через точки M, N и K,
лежащие на рёбрах
DA, AB и BС
соответственно.
M
L
C
A
P
K
N
B
7. Параллелепипед ABCDA1B1C1D1
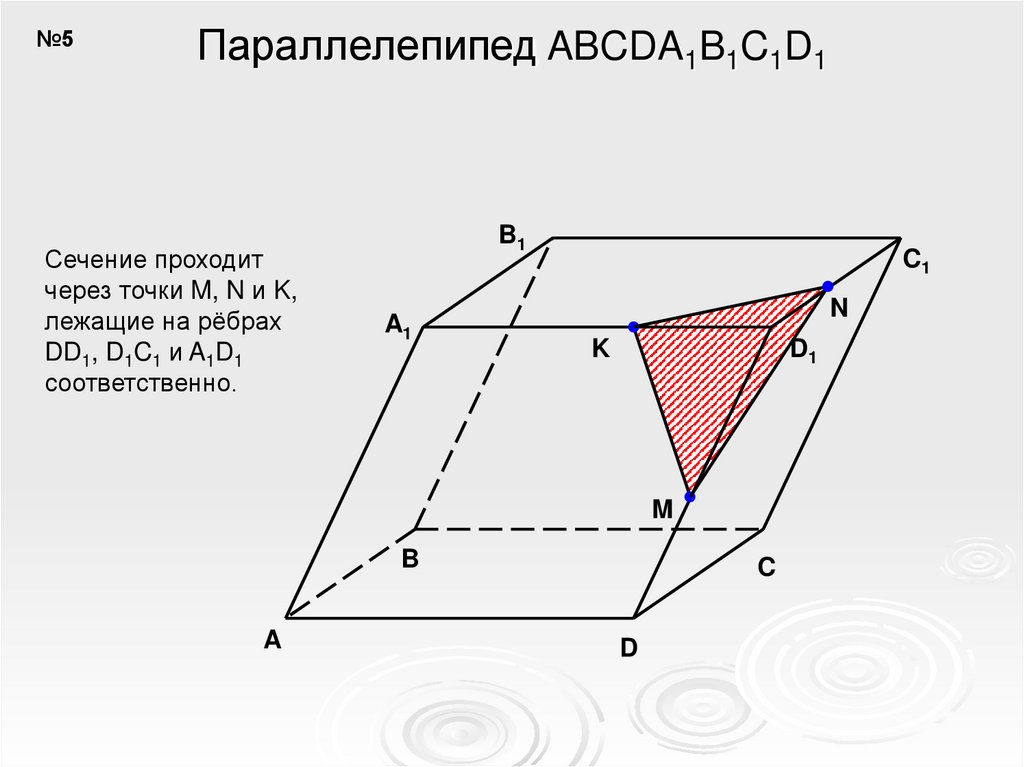
№5Параллелепипед ABCDA1B1C1D1
Сечение проходит
через точки M, N и K,
лежащие на рёбрах
DD1, D1C1 и A1D1
соответственно.
B1
A1
C1
N
K
D1
M
B
A
C
D
8.
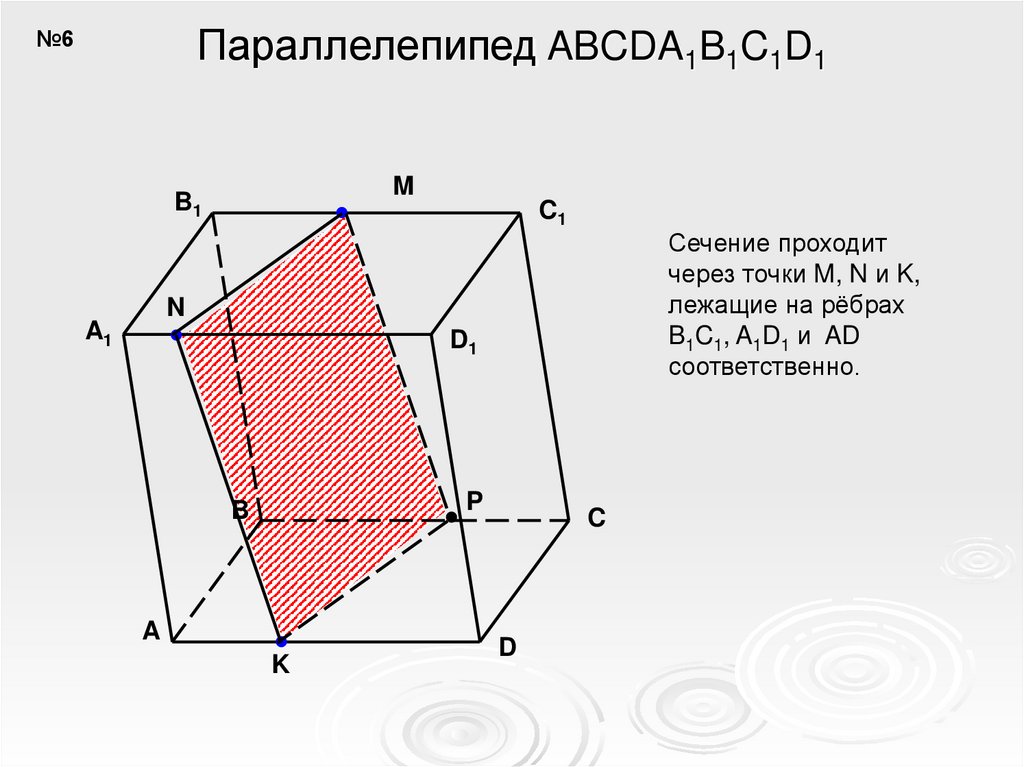
Параллелепипед ABCDA1B1C1D1№6
M
B1
C1
Сечение проходит
через точки M, N и K,
лежащие на рёбрах
B1C1, A1D1 и AD
соответственно.
N
A1
D1
P
B
A
K
C
D
9. Параллелепипед ABCDA1B1C1D1
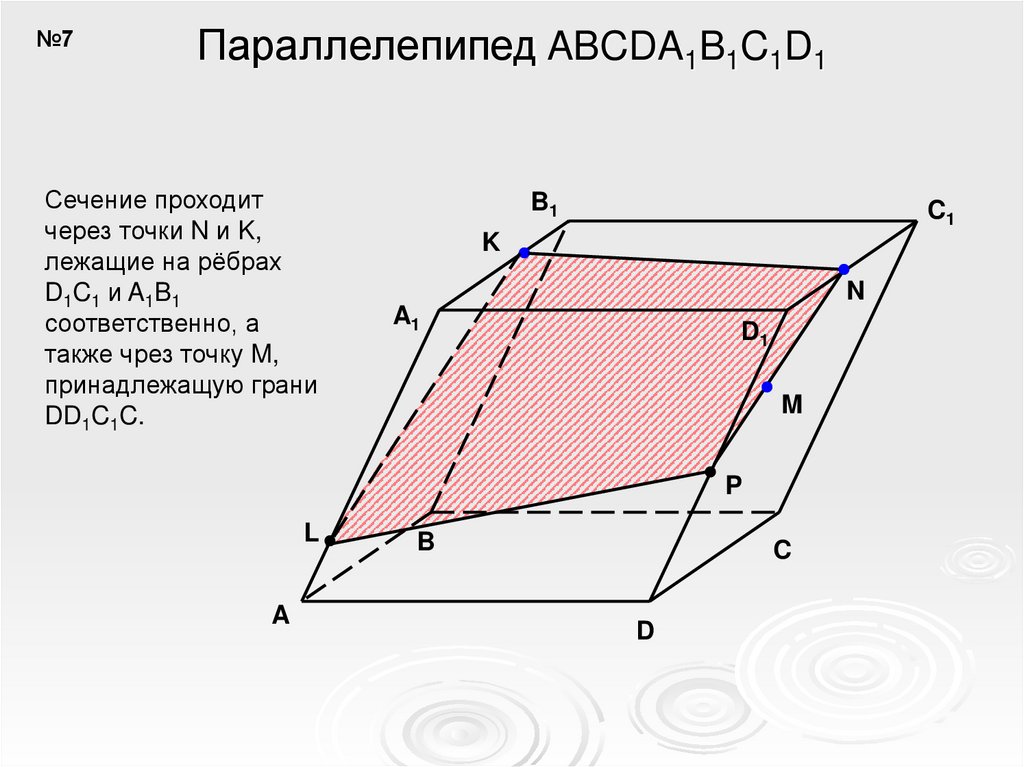
№7Параллелепипед ABCDA1B1C1D1
Сечение проходит
через точки N и K,
лежащие на рёбрах
D1C1 и A1B1
соответственно, а
также чрез точку M,
принадлежащую грани
DD1C1C.
B1
C1
K
N
A1
D1
M
P
L
A
B
C
D
10. Параллелепипед ABCDA1B1C1D1
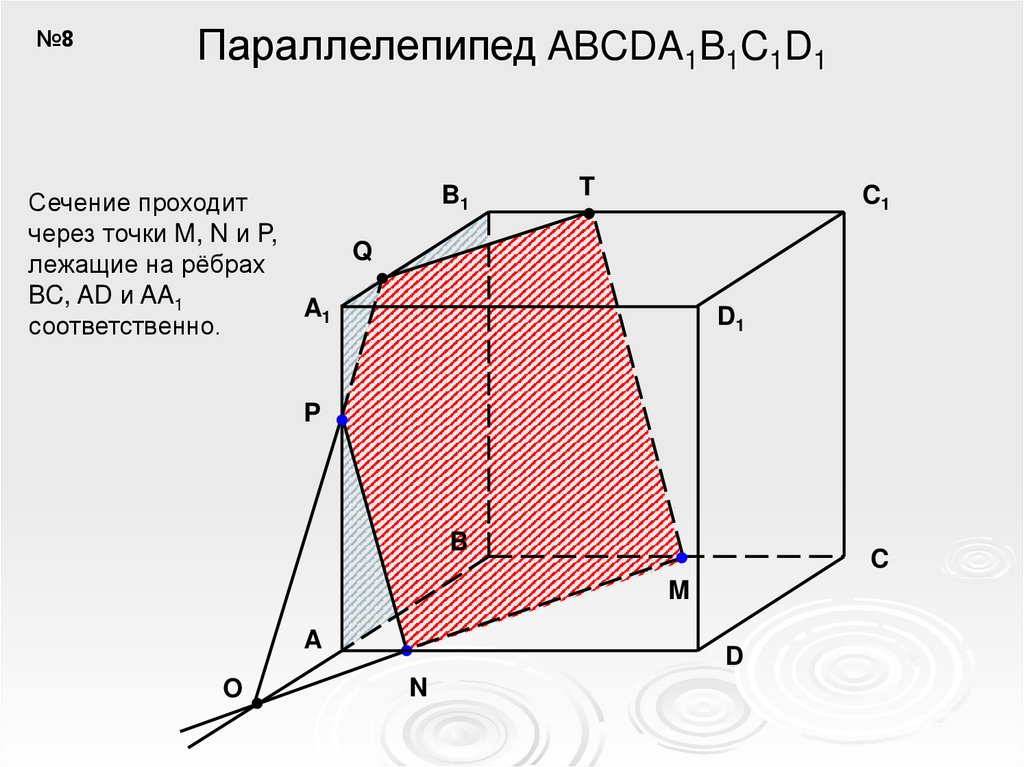
№8Параллелепипед ABCDA1B1C1D1
Сечение проходит
через точки M, N и P,
лежащие на рёбрах
BC, AD и AA1
соответственно.
B1
T
C1
Q
A1
D1
P
B
C
M
A
O
D
N
11.
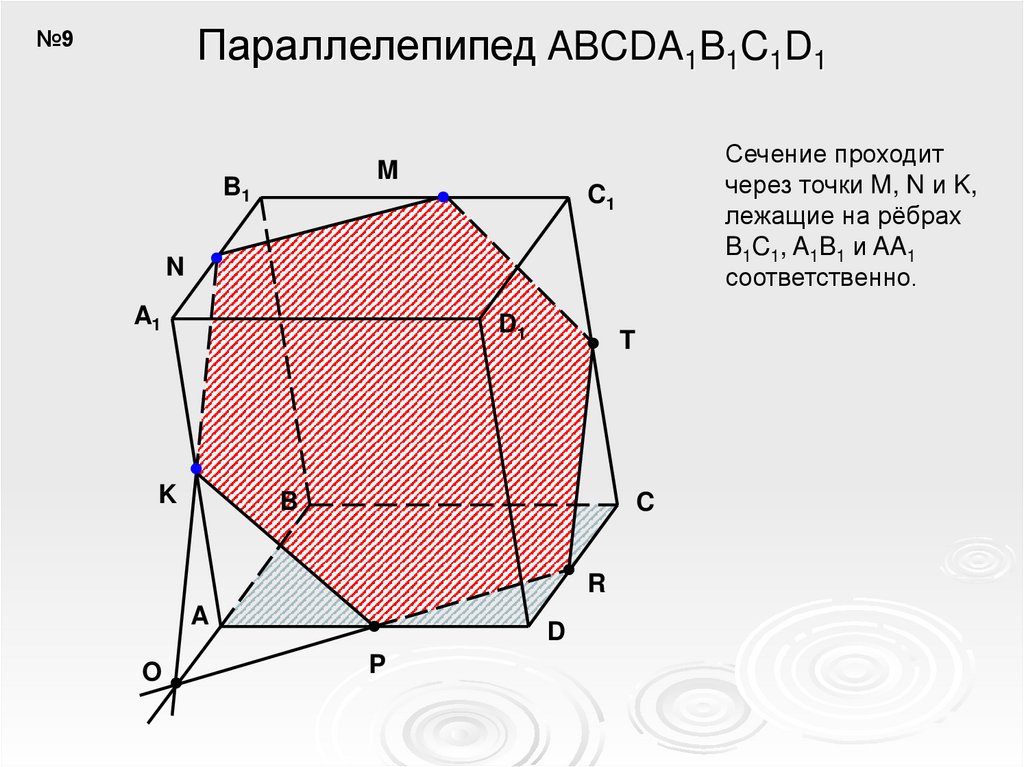
Параллелепипед ABCDA1B1C1D1№9
Сечение проходит
через точки M, N и K,
лежащие на рёбрах
B1C1, A1B1 и AA1
соответственно.
M
B1
C1
N
A1
D1
K
T
B
C
R
A
O
D
P
12.
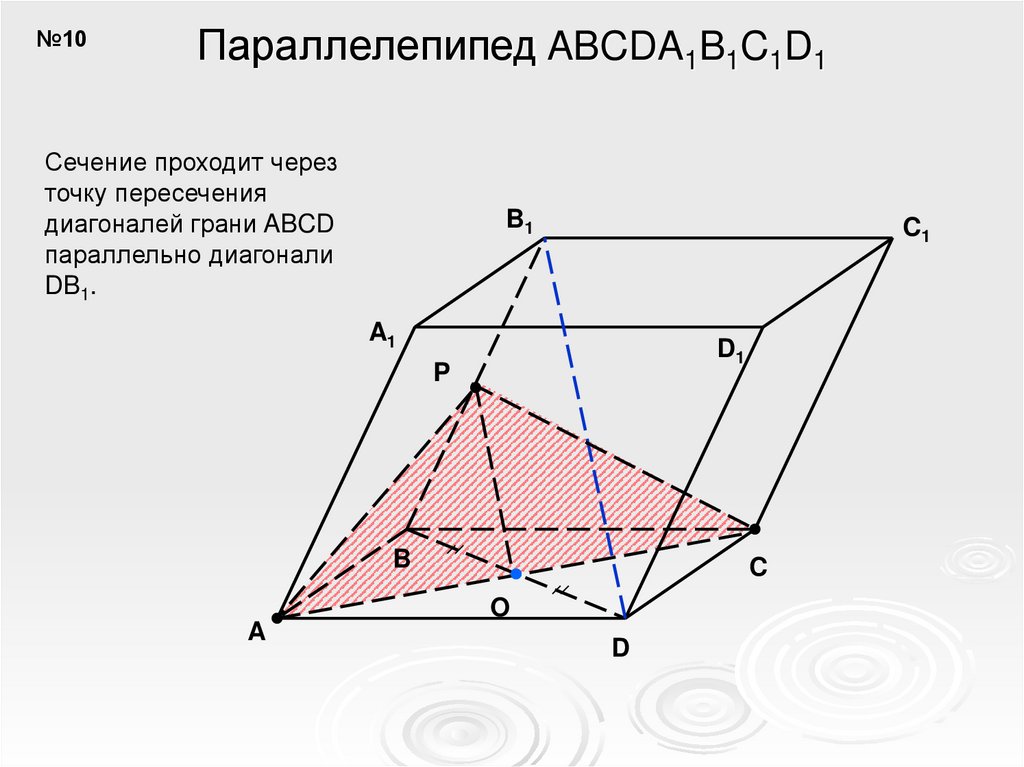
№10Параллелепипед ABCDA1B1C1D1
Сечение проходит через
точку пересечения
диагоналей грани ABCD
параллельно диагонали
DB1.
B1
C1
A1
D1
P
B
C
O
A
D
13.
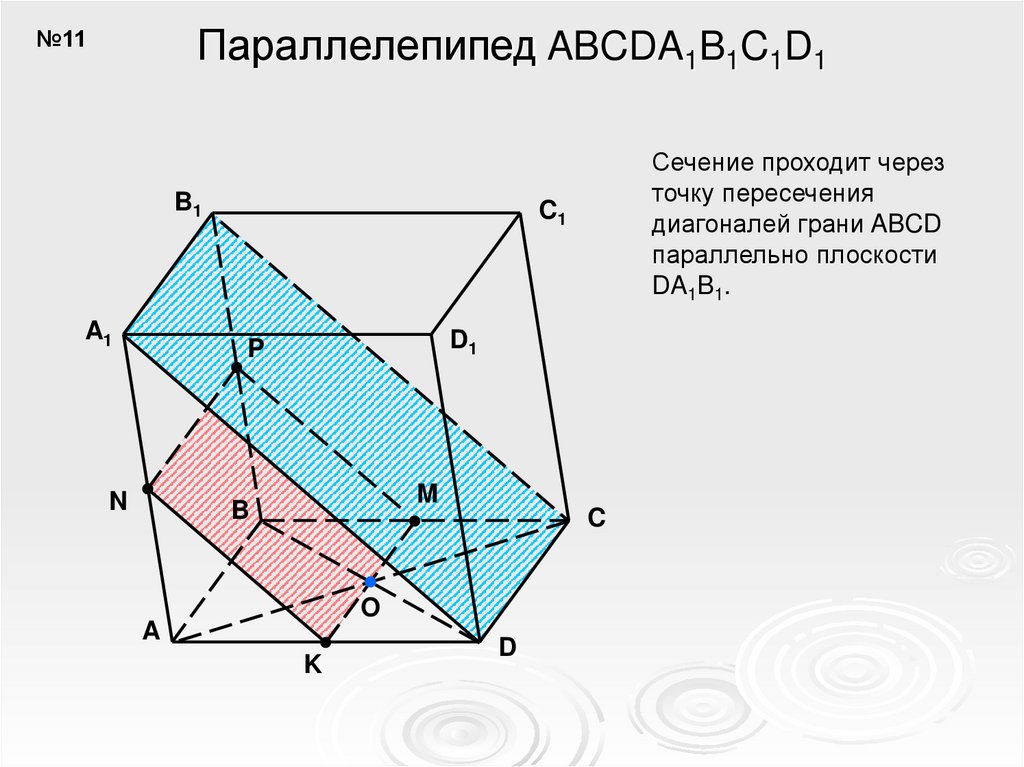
Параллелепипед ABCDA1B1C1D1№11
B1
A1
C1
D1
P
N
Сечение проходит через
точку пересечения
диагоналей грани ABCD
параллельно плоскости
DA1B1.
M
B
C
O
A
K
D
14.
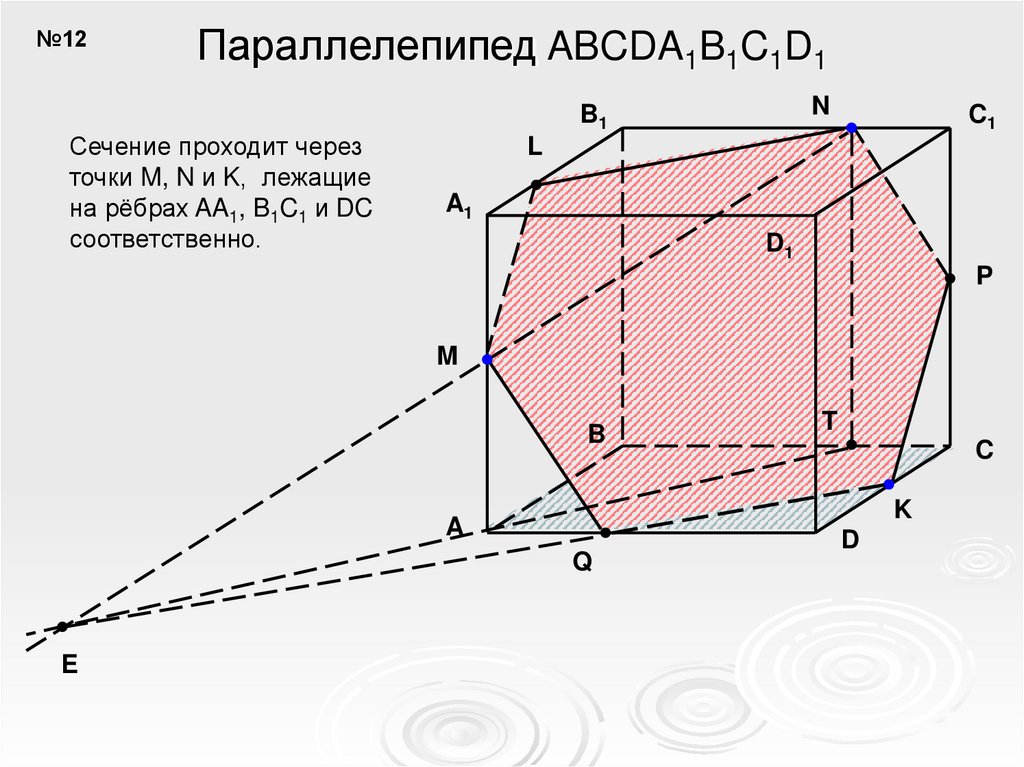
№12Параллелепипед ABCDA1B1C1D1
Сечение проходит через
точки M, N и K, лежащие
на рёбрах AA1, B1C1 и DC
соответственно.
N
B1
C1
L
A1
D1
P
M
B
C
K
A
Q
E
T
D
15.
Презентацию разработалМулёвкин Антон Михайлович
учитель информатики и математики МОУ Остафьевской средней общеобразовательной школы
Подольского района Московской области

 mathematics
mathematics








