Задачи на построение сечений

1.

Задачи на построение
сечений

2.

• Секущей плоскостью тетраэдра
(параллелепипеда) называется
любая плоскость, по обе стороны от
которой имеются точки данного
многогранника.
• Секущая плоскость пересекает грани
многогранника по отрезкам.
• Многоугольник, сторонами которого
являются эти отрезки, называется
сечением многогранника (тетраэдра,
параллелепипеда).

3.

Так как тетраэдр имеет четыре грани, то его
сечениями могут быть только треугольники и
четырёхугольники.

4.

Параллелепипед имеет шесть граней. Его
сечениями могут быть треугольники,
четырёхугольники, пятиугольники и
шестиугольники.
С
В
А
В
M
L
С
А
К
N
D
E

5.

Алгоритм построения сечений многогранников:
а) определить грани, с которыми секущая плоскость имеет
две общие точки, и провести через данные точки прямые;
б) определить грани, с которыми секущая плоскость имеет
одну общую точку, построить вторую общую точку и провести
через них прямую;
в) определить грани, с которыми секущая плоскость не имеет
общих точек, построить две общие точки, и провести через
них прямую;
г) выделить отрезки прямых, по которым секущая плоскость
пересекает ребра многогранника, заштриховать полученный
многоугольник.

6.

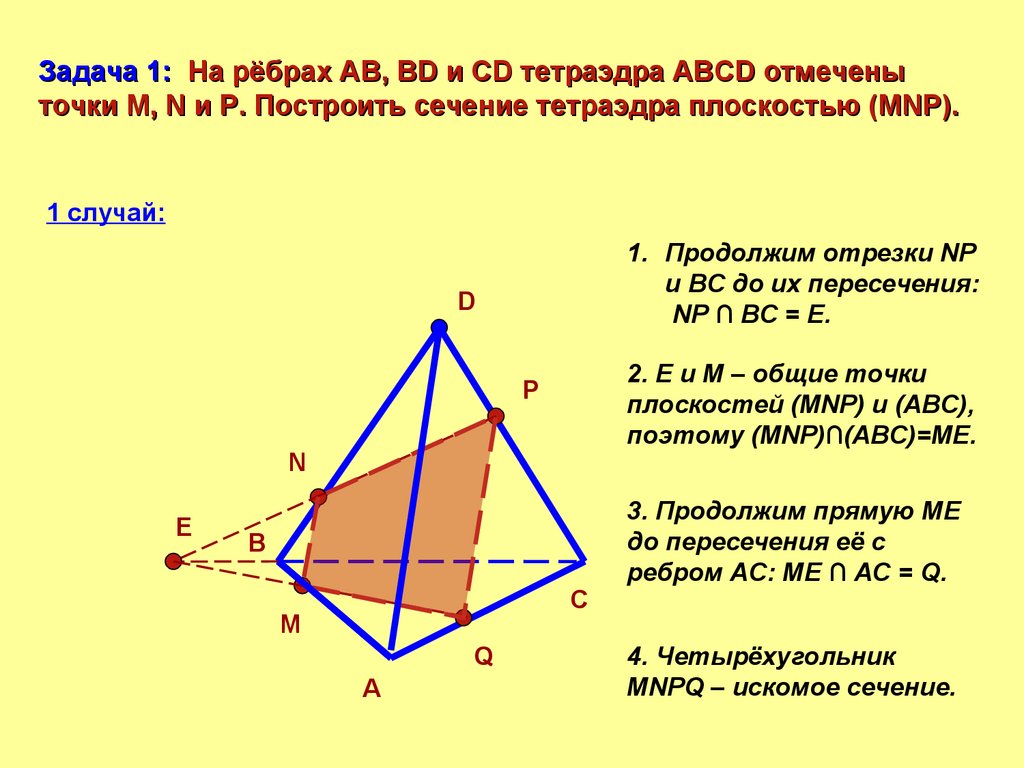
Задача 1: На рёбрах AB, BD и CD тетраэдра ABCD отмечены
точки M, N и P. Построить сечение тетраэдра плоскостью (MNP).
1 случай:
1. Продолжим отрезки NP
и BC до их пересечения:
NP ∩ BC = E.
D
2. Е и М – общие точки
плоскостей (MNP) и (ABC),
поэтому (MNP)∩(ABC)=МЕ.
P
N
E
B
С
М
Q
А
3. Продолжим прямую МЕ
до пересечения её с
ребром АС: МЕ ∩ АС = Q.
4. Четырёхугольник
MNPQ – искомое сечение.

7.

2 случай: прямые NP ll BC.
D
Если NP ll BC, то NP ll
(АBC), тогда
(MNP) ∩ (ABC) = MQ.
N
P
B
Причём MQ ll NP.
C
M
Q
A
Четырёхугольник MNPQ –
параллелограмм.

8.

Задача 2: Точка М лежит на боковой грани АDВ тетраэдра DАВС.
Построить сечение тетраэдра плоскостью, проходящей через
точку М, параллельно основанию АВС.
D
1. Через точку М проведём
прямую PQ, параллельную
отрезку АВ.
Q
R
2. Через точку Р проводим
прямую PR, параллельную
отрезку АС(Rє DC).
М
Р
В
С
А
3. ΔPQR – искомое сечение.

9.

Задача 3: На рёбрах параллелепипеда даны три точки А, В и С.
Постройте сечение параллелепипеда плоскостью (АВС).
рис. 39а
рис. 39б
1. Провести АВ и ВС.
2. АЕ ıı ВС, СD ıı АВ.
С
А
В
В
С
А
D
Провести отрезки АВ, ВС и СА
E
3. Провести отрезок ЕD.

10.

Задача 3: На рёбрах параллелепипеда даны три точки А, В и С.
Постройте сечение параллелепипеда плоскостью (АВС).
(рис. 39в)
1. АВ ∩ а = М
2. Проведём через (·) М
прямую b ıı ВС.
С
В
D
3. Через (·) Е проведём
прямую, параллельную АВ,
и получим (·) D.
А
а
М
b – прямая, по которой
пересекаются секущая
плоскость и плоскость
нижнего основания.
E
b
F
4. Проводим отрезки AF и
CD.
5. ABCDEF – искомое
сечение.

11.

Решение задач на
построение сечений

12.

Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

13.

Задача 2. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
впринадлежащие
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
Аточке
АА
ВС1В.
1В
11
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

14.

Задача 3. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 =
5. LF
F
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

15.

Задача: На рёбрах AD и DC тетраэдра DABC взяты точки Е и К.
Постройте точку пересечения прямой ЕК и плоскости (АВС).
D
Е
К
В
А
С
М

16.

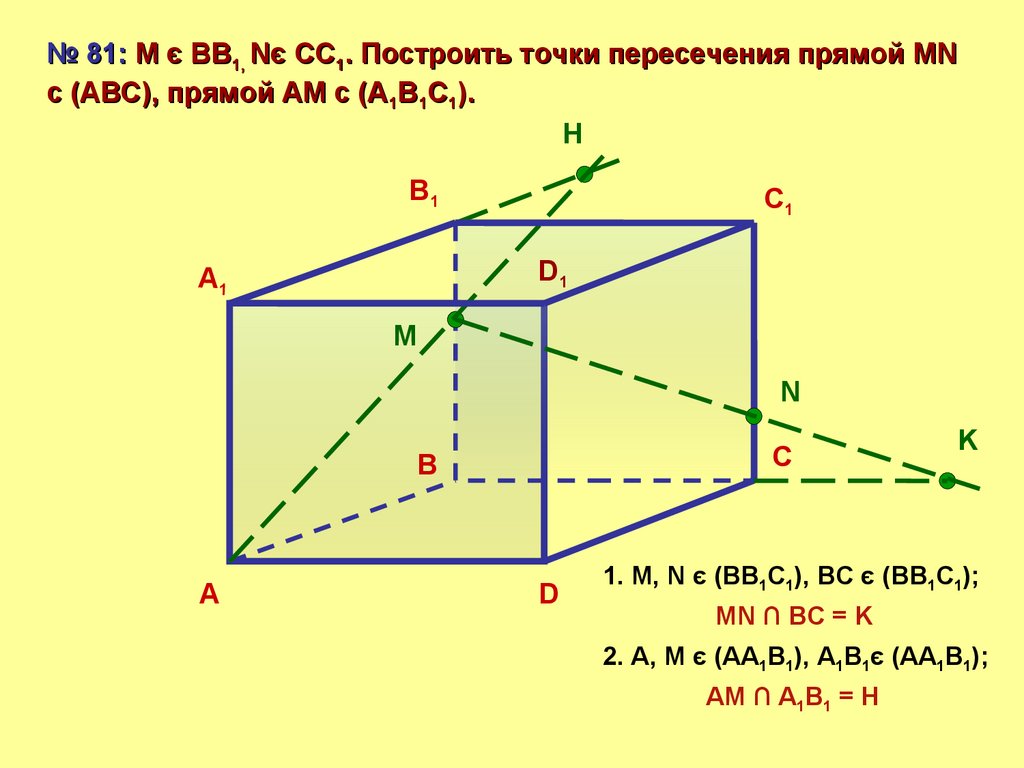
№ 81: М є ВВ1, Nє СС1. Построить точки пересечения прямой MN
с (АВС), прямой АМ с (А1В1С1).
H
В1
С1
D1
А1
М
N
С
В
А
D
K
1. M, N є (BB1C1), BC є (BB1C1);
MN ∩ BC = K
2. A, M є (AA1B1), A1B1є (AA1B1);
AM ∩ A1B1 = H

17.

№ 82в: М є (АА1В1). Постройте сечение, проходящее через точку М,
параллельно плоскости (BDD1).
В1
С1
N
А1
D1
K
M
В
С
P
А
L
D
1. PN ll BB1, NK ll B1D1,
KL ll DD1, PL ll BD.
2. Mє(PNK), (PNK) ll (BDD1)

18.

№ 83: Постройте сечение, проходящее: а) через СС1 и точку
пересечения диагоналей грани АА1D1D; б)точку пересечения
диагоналей грани ABCD параллельно плоскости АВ1С1.
В1
Е
А1
D1
М
А
С1
В
С
1. EF ll CC1(MєEF)
F
D
2. Отрезки EC1 и FC
3. ЕС1СF – искомое
сечение.

19.

№ 83б
В1
С1
D1
А1
N
O
В
С
К
М
А
1. Построим KL ll AD,где
(·) M є KL
2. Затем LN ll DC1, KO ll AB1
L
D
3. Строим отрезок ON
4. KLNO – искомое
сечение

20.

№ 84: Построить сечение проходящее через точки B1, D1 и
середину ребра CD.
А1
D1
С1
В1
А
D
E
В
F
С

21.

№ 85: Построить сечение (BKL), где К и L – середины рёбер АА1 и
СС1 соответственно.
D1
А1
С1
В1
E
K
L
D
А
С
В
1. Строим отрезки BK и BL.
3. Затем провели KD1 ll AE.
2. Проводим AE ll BL.
4. И построили отрезок D1L.
5. BKD1L – искомое сечение.

22.

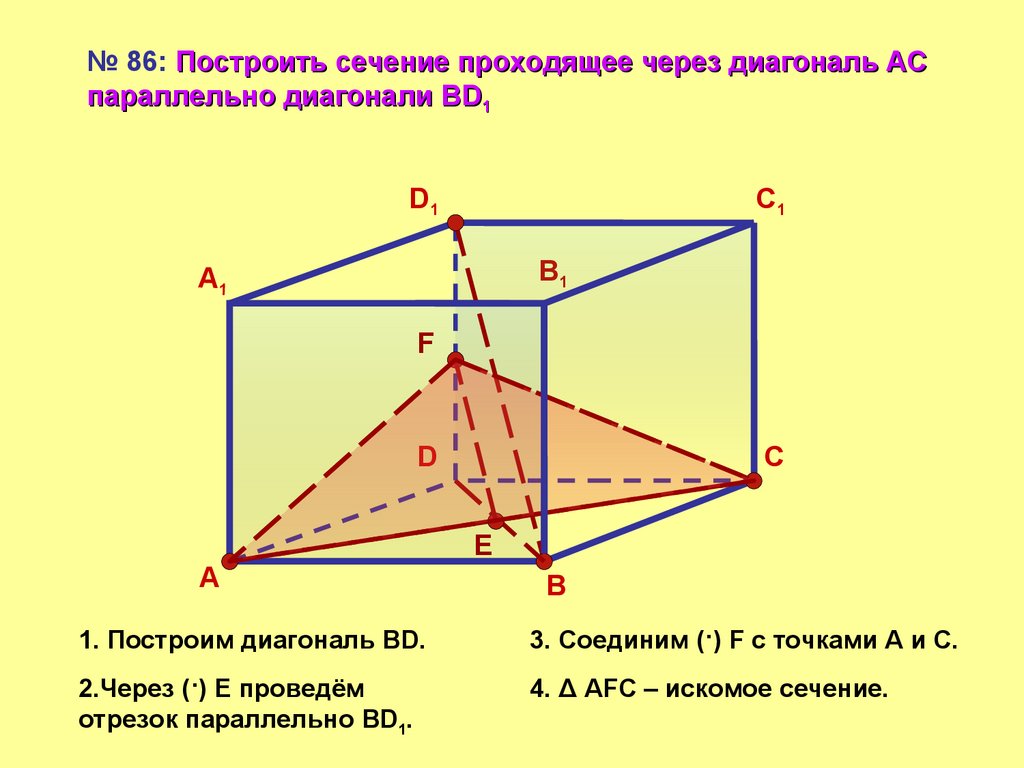
№ 86: Построить сечение проходящее через диагональ АС
параллельно диагонали BD1
D1
С1
В1
А1
F
D
С
E
А
В
1. Построим диагональ BD.
3. Соединим (·) F c точками А и С.
2.Через (·) Е проведём
отрезок параллельно BD1.
4. Δ AFC – искомое сечение.

23.

№ 87а: Постройте сечение плоскостью (MNK), где М є ВВ1, Nє AA1,
K є AD.
A1
D1
B1
C1
M
N
A
K
B
L
D
O
P
C
1. MN и NK
2. ML ll NK
3. NK ∩ D1D = O
4. LO ∩ DC = P;PL
5. KP

24.

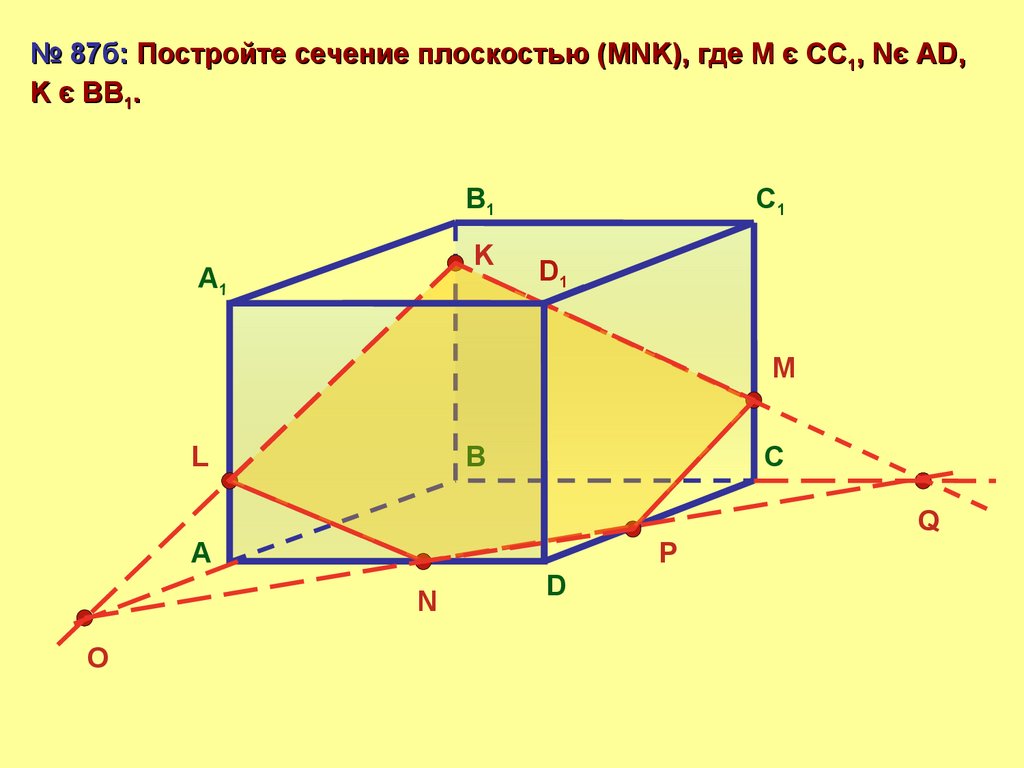
№ 87б: Постройте сечение плоскостью (MNK), где М є СС1, Nє AD,
K є BB1.
В1
K
А1
С1
D1
M
L
В
С
Q
А
P
N
O
D

25.

Д/з: п.14, разобрать все задачи в презентации,
оформить решение и построение в тетради.
Фото классной и домашней работы отправить
в Тимс. Подготовиться к контрольной работе
по главе 1.