Similar presentations:
Температурный ангармонизм. Рассеяние Мандельштама-Бриллюэна. Вынужденное рассеяние Мандельштама-Бриллюэна
1. Температурный ангармонизм Рассеяние Мандельштама-Бриллюэна Вынужденное рассеяние Мандельштама-Бриллюэна
Температурный ангармонизмРассеяние Мандельштама-Бриллюэна
Вынужденное рассеяние МандельштамаБриллюэна
2.
Температурный ангармонизмВынужденное рассеяние Мандельштама-Бриллюэна.
Связанные уравнения
В случае бигармонической накачки связанные уравнения для электромагнитных
волн имеют вид
2
2
4
1
1 NL
E
P
1
2 2 1
2
c t
c
4 22 NL
2 2
2
2 2 E2 2 P
c t
c
нелинейная поляризация
и решаются совместно с уравнением для оптического возбуждения
акустической волны
где
2
2 2
вынуждающая сила
2 2 v f
t
t
- постоянная затухания (полуширина линии спонтанного РМБ)
v - скорость акустической волны
- локальное изменение плотности
3.
Температурный ангармонизмВынужденное рассеяние Мандельштама-Бриллюэна.
Связанные уравнения
Правые части уравнений – результат нелинейного взаимодействия всех трех
волн ( E1 , E2 , ):
1
E2
4
1
P NL 2
E1
4
1
f p E1 E*2
2
P NL 1
где
p - электрострикционное давление
0
- коэффициент электрострикции
0 - плотность среды
4 12 NL
1 2
1
2 2 E1 2 P
c t
c
4 22 NL
2 2
2
2 2 E2 2 P
c
t
c
2
2 2
2 2 v f
t
t
4.
Температурный ангармонизмВынужденное рассеяние Мандельштама-Бриллюэна назад
ММА
Эту задачу параметрического взаимодействия решаем методом ММА:
2
i
1
i kz
E
E
(
)
e
1
2
0
z 2
2k1c 2
4 12 NL
1 2
1
2 2 E1 2 P
c t
c
2
i
2
i kz
E
E
(
)
e
2
0
2 1
z
2
2k2 c
4 22 NL
2 2
2
2 2 E2 2 P
c
t
c
ika
i kz
(
)
E
E
0
0
1 2 e
2
z v
4 v
где
2
2 2
2 2 v f
t
t
ik z i a t
,
E1 E1eik1 z i 1t , E2 E2 e ik2 z i 2t , ( )0 e a
частота и волновой вектор вынужденной акустической волны
a 1 2 , ka a / v
волновая расстройка k k1 k2 ka
- постоянная затухания
5.
Температурный ангармонизмВРМБ в условиях сильного поглощения акустической волны
В реальных средах (жидкостях) затухание велико тогда воспользуемся приближением
( )0 z i k ( )0
получим
i 2 12
2
(3)
E
E
1
MB 2 E1
2
z 2
k1c
2
i
2
2 (3)
2
E
E
2
MB 1 E2
2
z 2
k2 c
/ v 104 см-1
i 12
i kz
E
(
)
e
E1
2
0
z 2
2k1c 2
2
i
2
i kz
E
E
(
)
e
2
1
0
z 2
2k2 c 2
ika
i kz
(
)
E
E
e
0
0
1
2
z v
4 v 2
где кубичная восприимчивость, ответственная за ВРМБ:
(3)
MB
ka 0
4 v k i / v
2
6.
Температурный ангармонизмПриближение заданной накачки в ВРМБ
поскольку
(3)
Im MB
0
2
то E2 нарастает в направлении назад
i
2
1
2
(3)
E
E1
при выполнении условия превышения усиления E1
2
MB
2
z 2
k1c
над потерями:
2
i
2
2 (3)
2
2 2
E
E
2
2
MB 1 E2
(3)
2
k2 c
2
Im MB E1
z
2
2
k2 c
В приближении заданного поля накачки
E2 ( z ) E1 (l ) e(GMB )( l z )
2
2
с коэффициентом усиления ВРМБ
G MB
2
4 22
( 3)
2 Im MB E1
k2 c
7.
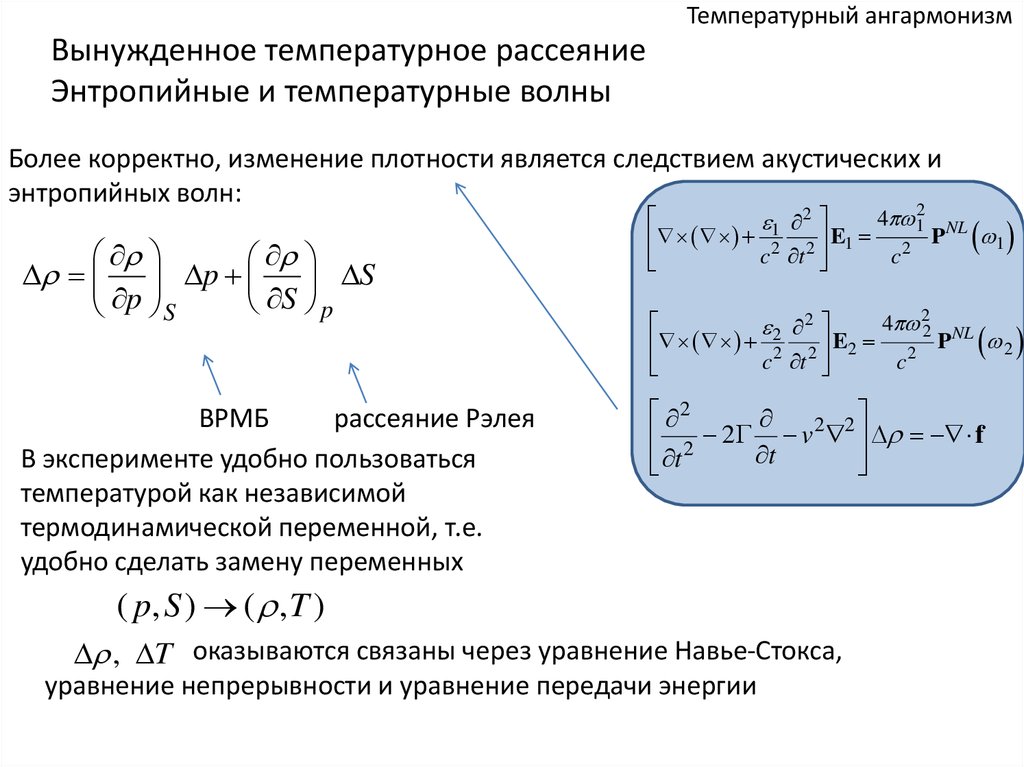
Температурный ангармонизмВынужденное температурное рассеяние
Энтропийные и температурные волны
Более корректно, изменение плотности является следствием акустических и
энтропийных волн:
2
p S
S p
p S
ВРМБ
рассеяние Рэлея
В эксперименте удобно пользоваться
температурой как независимой
термодинамической переменной, т.е.
удобно сделать замену переменных
4 1 NL
1 2
E
P
1
2 2 1
2
c t
c
4 22 NL
2 2
2
2 2 E2 2 P
c
t
c
2
2 2
2
v
f
2
t
t
( p, S ) ( , T )
, T оказываются связаны через уравнение Навье-Стокса,
уравнение непрерывности и уравнение передачи энергии
8.
Температурный ангармонизмВынужденное температурное рассеяние.
Уравнение Навье-Стокса и уравнение непрерывности
v 2 T 0
v v 2
o ( )
( T ) 2 v
t
1
E1 E2
E
E
1
2 T
2
2 T
0 v 0
t
и
где
Cp
- отношение теплоемкостей
Cv
T
- изотермическая сжимаемость
- коэффициент затухания акустической волны
T
0
- коэффициент электрострикции
9.
Температурный ангармонизмВынужденное температурное рассеяние.
Уравнение Навье-Стокса и уравнение непрерывности
Эту систему можно преобразовать
в уравнение
v 2 T 0
v v 2
o ( )
( T ) 2 v
t
1
E1 E 2
E1 E2 T
2
2 T
0 v 0
t
2 v2 2 2
v 2 T 0 2
( )
( T )
2
0 t
t
2
1
E1 E 2
E
E
1
2 ( T )
2
2 T
которое при T 0 сводится к уравнению для акустической волны
2
2 2
2 1
2 2 v ( ) E1 E1
t
2
t
10.
Температурный ангармонизмВынужденное температурное рассеяние.
Уравнение передачи энергии
C 2 T Cv ( 1)
0 v
T
t
T
t
nc
1
E1 E2
T0E1 E2
2 T
t
T - теплопроводность
- линейный коэффициент поглощения
при условии
приводит к
1, 0, T 0
T 0
11.
Вынужденное температурное рассеяние.Полная система уравнений
2
2
4
1
1 NL
E
P
1
2 2 1
2
c t
c
4 22 NL
2 2
2
2 2 E2 2 P
c t
c
Температурный ангармонизм
нелинейные волновые
уравнения
Навье-Стокс
2 v2 2 2
v 2 T 0 2
( )
( T )
2
0 t
t
2
1
E1 E2
E
E
(
T
)
1
2
2
2 T
C 2 T Cv ( 1)
уравнение передачи
0 v
T
t
T
t
энергии
nc
1
E1 E2
T0E1 E2
2 T
t
12.
Вынужденное температурное рассеяние.Нелинейные поляризации и ММА
P NL 1
P NL 2
1
E2
4 0
4
1
E1
4 0
4
Температурный ангармонизм
E2 T
T
E1 T
T
1
E1
4
T
0
2
2
2
E
E
E
1
1
2
z
2
2
2
E
E
E
2
1
2
z
используя приближение
1
E2
4
P NL 2
уравнения ММА запишутся в виде
T
P NL 1
T
T
13.
Вынужденное температурное рассеяние.Коэффициент усиления
MB
1
1 /
2
a
MB
«нормальное»
ВРМБ
k1 k2 v
1 2
1/2
2 /
1 /
температурное
ВРМБ
- частотная
расстройка
MB
22 2
22 a
a
, MB
2
4 c 0v
8 c 2 0v
RL
22 R
22 a
a
, RL
2
4 c 0v RL
4 c 2 0v RL
a vc T
R 1 c RL
,
C p 2
4nv 2
2
2
Температурный ангармонизм
a
RL RL
1
2 a / RL
a
/ RL
2
рассеяние Рэлея
2
2
2
E1 E1 E2
z
T
0
- коэффициенты усиления ВРМБ
- коэффициенты усиления
рассеяния Рэлея
k1 k2
T k1 k2
, RL
0
0C p
2
2












 physics
physics








