Энергетические уровни. Спонтанное и вынужденное излучения. Лекция 2

1. Лазеры

Light
Amplification
by
Stimulated
Emission
of
Radiation
Лазеры
Означает
«усиление
света
с помощью
вынужденного
испускания
излучения»

2.

Лекция №2
2.1. Собственные состояния системы.
2.2. Квантовые переходы.
А. Спонтанное излучение.
Б. Вынужденное поглощение излучения.
В. Вынужденное, индуцированное излучение.
С. Активная усиливающая (инверсная) среда.
2.3. Основа работы ОКГ.
А. Необходимое условие усиления – инверсная заселенность.
Б. Коэффициент поглощения (усиления) системы.
В. Связь между коэффициентом поглощения и инверсной заселенностью
уровня.
С. Коэффициент потерь.
Д. Положительная обратная связь.
Е. Развитие процесса генерации в лазере.
К. Насыщение усиления.

3. Продолжение

2.4. Форма и естественная ширина спектральной
линии.
А. Форма спектральной линии.
Б. Уширение спектральной линии.
В, Энергетические уровни.
С. Связь ширина линии с длиной волны.
2.4.1. Доплеровской уширение.
2.4.2. Уширение при столкновениях.
2.4.3. Уширение в твердых телах.
2.4.4. Уширение в Н- и Е- полях.
2.4.5. Однородное и неоднородное уширение.

4. 2.1 Собственные состояния системы

Один из основных выводов квантовой механики
гласит, что каждая физическая система может
находиться только в одном из заданных
энергетических соотношений так называемых
собственных состояний системы. С каждым из
этих состояний мы связываем энергию, которая
соответствует полной энергии системы, если все
состояния заняты. Классическими примерами,
квантовой
механики
является:
свободный
электрон, атом водорода или гармонический
осциллятор. Примерами более сложных систем
могут
служить
молекула
водорода
и
полупроводниковый кристалл.

5.

С каждым состоянием (i) атома водорода мы можем
связать
следующую
собственную
функцию
i
Ei
t
, где i (r ) dxdydz - вероятность
нахождения электрона, о котором известно, что он
находится
в
состоянии
i
в
пределах
электромагнитного объема dxdydz с центром в точке r,
Ei – энергия состояния, описанного выше, при этом
( r , t ) i ( r )e
h
2
2
, h=6,626·10-34 Дж·с – постоянная Планка.
Определение собственных функций i (r ) и
соответственно энергии Ei различных физических
систем является одной из главных задач квантовой
механики. Мы с Вами в данной дисциплине примем
как данное существование их состояний их
энергетических уровней, а также ряд других
результатов, правомерность которых доказана
экспериментально.

6. Ансамбль частиц

7. Кратность вырождения

8. Взаимодействие электромагнитного излучения с атомом

9.

10. Коэффициенты Эйнштейна

11. Плотность энергии излучения

12.

13. 2.2 Квантовые переходы.

14.

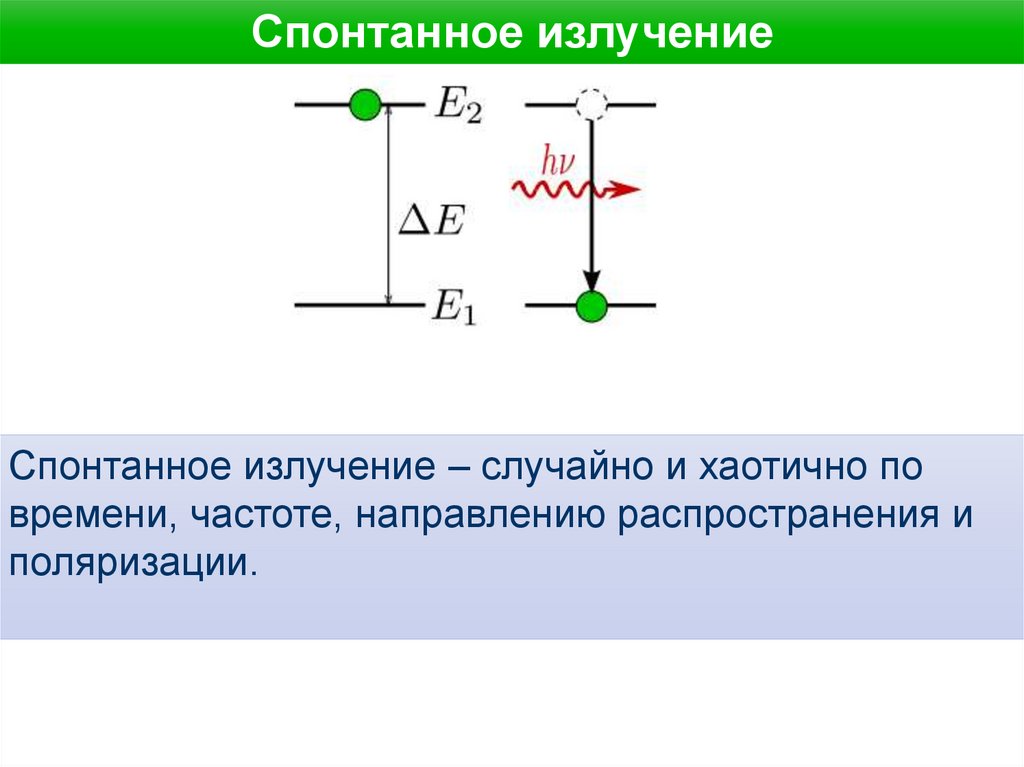
Спонтанное излучение
Спонтанное излучение – случайно и хаотично по
времени, частоте, направлению распространения и
поляризации.

15. Спонтанное излучение

1
(tсп ) nm Anm

16. Вынужденное поглощение излучения

17.

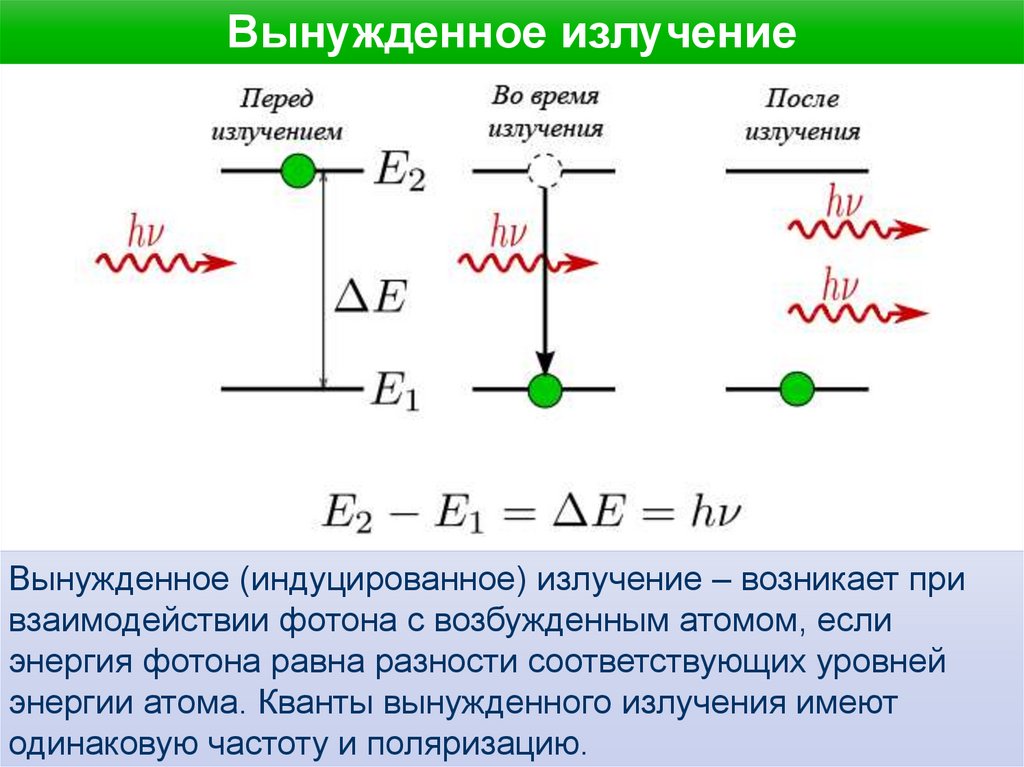
Вынужденное излучение
Вынужденное (индуцированное) излучение – возникает при
взаимодействии фотона с возбужденным атомом, если
энергия фотона равна разности соответствующих уровней
энергии атома. Кванты вынужденного излучения имеют
одинаковую частоту и поляризацию.

18. Вынужденное, индуцированное излучение

19.

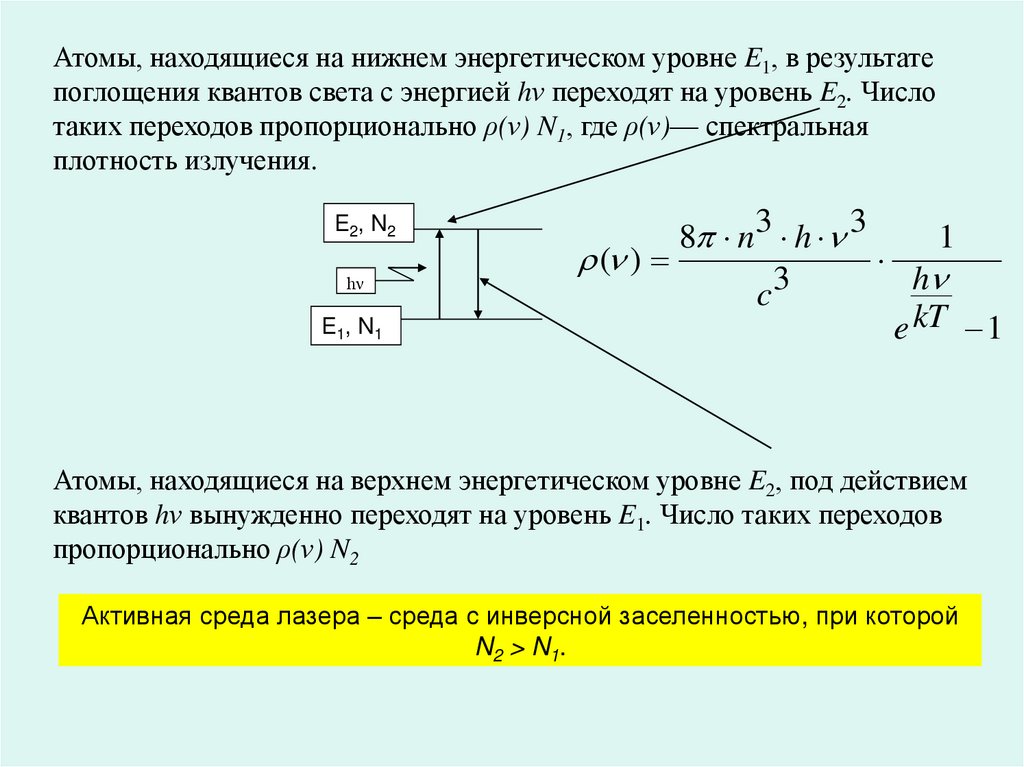
Атомы, находящиеся на нижнем энергетическом уровне E1, в результате
поглощения квантов света с энергией hν переходят на уровень E2. Число
таких переходов пропорционально ρ(ν) N1, где ρ(ν)— спектральная
плотность излучения.
E2, N2
hν
E1, N1
8 n3 h 3
1
( )
3
h
c
e kT 1
Атомы, находящиеся на верхнем энергетическом уровне E2, под действием
квантов hν вынужденно переходят на уровень E1. Число таких переходов
пропорционально ρ(ν) N2
Активная среда лазера – среда с инверсной заселенностью, при которой
N2 > N1.

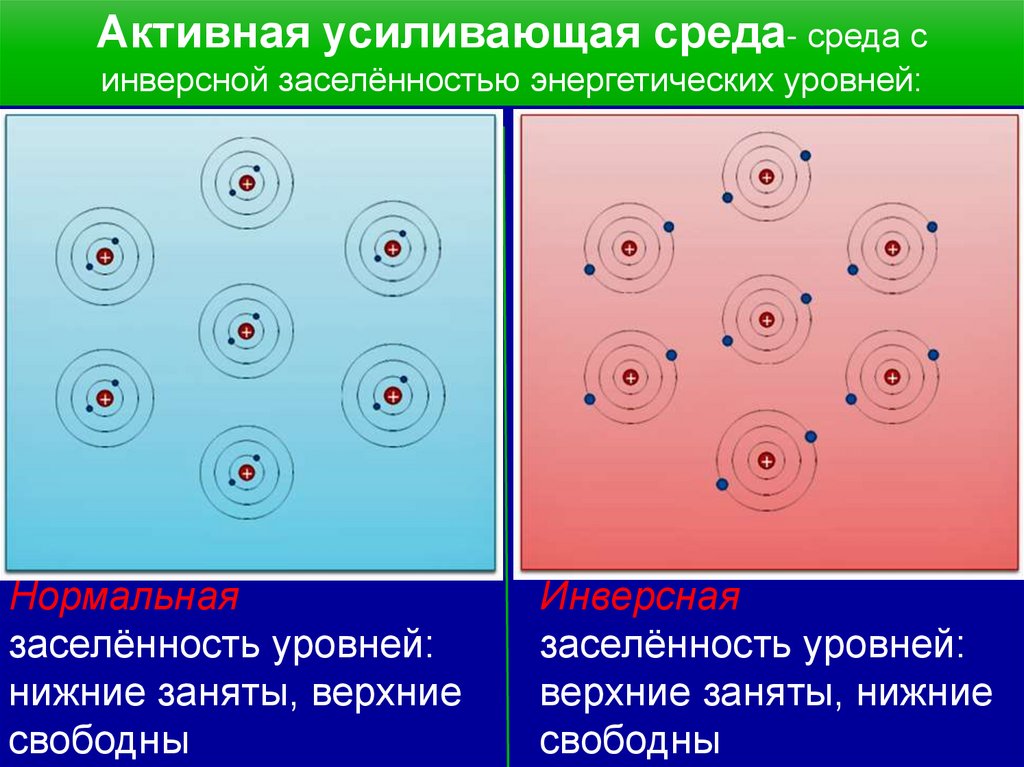
20.

Активная усиливающая среда- среда с
инверсной заселённостью энергетических уровней:
Нормальная
заселённость уровней:
нижние заняты, верхние
свободны
Инверсная
заселённость уровней:
верхние заняты, нижние
свободны

21. Принцип действия лазеров

22.

23. Накачка – осуществление инверсии

24. Усиление световой волны

25. Инверсия

26.

27. Закон Бугера

28. О резонаторе

29. Необходимые элементы лазера

30. 2.3. Основа работы ОКГ

31. Необходимое условие усиления – инверсная заселенность

32. Коэффициент поглощения (усиления) системы

33. Связь между коэффициентом поглощения и инверсной заселенностью уровня

34. Коэффициент потерь

35. Положительная обратная связь

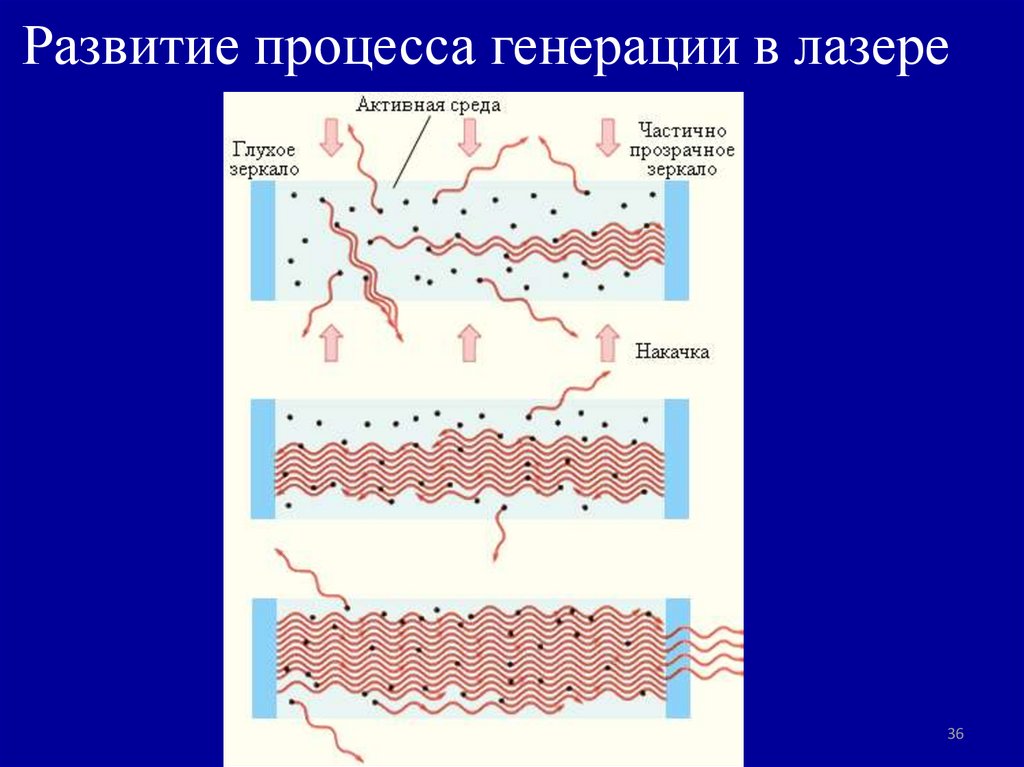
36. Развитие процесса генерации в лазере

36

37. Насыщение усиления

38. Поглощение излучения средой.

Если на ансамбль квантовых частиц, находящийся в состоянии
ТДР, падает внешнее излучение, частота которого находится в
резонансе с энергией ΔE квантового перехода, то, поскольку N1>N2
(если g1=g2), скорость поглощения превосходит скорость
индуцированных переходов (Fп > Fи (см. табл. 1.2)) и в целом имеет
место поглощение этого излучения средой.
Таблица 1.2. Виды связанных с излучением переходов в квантовых
системах и их параметры
Тип перехода
Без внешнего
излучения
Параметр
перехода
Вероятность, с-1
Скорость перехода,
см–3с–1
Удельная мощность,
Вт.см–3
Полная мощность,
Вт.
Pc
С внешним (резонансным) излучением
Спонтанное
излучение
Wc A21
Поглощение
Wп B12
Вынужденное
(индуцированное)
излучение
Wи B21
Fc n2 A21,
Fп n1B12
Fu n2 B21
(1.6)
Pc h 21n2 A21,
Pп h 21n1B12
Pu h 21n2 B21
(1.7)
полн
h 21n2 A21V ,
Pп
полн
h 21n1B12 V
Pu
полн
h 21n2 B21 V (1.8)

39. Эффект насыщения поглощаемой мощности

В процессе поглощения происходит уменьшение числа частиц на нижнем уровне
«1» и увеличение – на верхнем уровне «2», т.е. имеет место выравнивание
населённости уровней, и, как следствие,– снижение эффекта поглощения.
Очевидно, что в предельном случае, при ρ→∞ это выравнивание становится
полным, т.е. n1≈n2, поглощение прекращается, и падающее излучение будет
проходить через среду без потерь. Такая ситуация называется насыщением
населённости уровней «1» и «2». С другой стороны, т.к. спонтанные переходы,
не связанные с наличием внешнего излучения, продолжают опустошать уровень
«2», пропорциональная часть падающего излучения всё же будет поглощаться и
затем сразу же излучаться спонтанными переходами с верхнего уровня – на
нижний уровень.
Пусть на ансамбль частиц, первоначально находящийся в состоянии ТДР, падает
монохроматическое излучение, частота ν которого находится в резонансе с
квантовым переходом («попадает» в его контур поглощения), например, 0 .
Найдем значение мощности этого излучения ΔР, поглощаемой средой, и
зависимость этой мощности от плотности энергии ρ падающей волны.

40.

Обозначим через Рпогл – удельную мощность при переходах с
поглощением, а Ринд
– удельную мощность, выделяемую при
индуцированных переходах под действием того же излучения.
Вследствие преобладания скорости поглощения над скоростью
индуцированного излучения, для величины эффективной удельной
поглощаемой мощности, можно записать
P P погл Ринд h Wи (
g2
n1 n2 ) h Wи n .
g1
(1.30,а)
В (1.30,а), в соответствии с Wи B21 S ( 0 ) , и введено обозначение:
g2
( n1 n2 ) n .
g1
Положим для простоты, что g1 g2 и, обозначив Wп Wи W , получим
P h W n .
(1.30,б)
Поскольку теперь Δn = n1–n2, а n1+n2=n0 — суммарная концентрация
частиц на рассматриваемых уровнях в ансамбле, n2 найдём из
стационарного кинетического уравнения:
dn2
n
2 W n 0 .
dt
2

41.

n
И тогда для Δn получим:
n0
,
1 2W 2
(1.31),
а так как W B21 S ( 0 ) , найдём, что с ростом ρ падающего
излучения разность населённостей уровней Δn снижается.
Введём параметр насыщения для плотности энергии падающего
излучения: 0
1
, и тогда для (1.31) получим:
2 B21 2 S ( 0 )
n
n 0 .
1
0
(1.32, а)
Очевидно, что при ρ=ρ0, величина Δn снижается вдвое. Переходя от
плотности энергии ρ – к интенсивности излучения (плотности потока
мощности) I=ρ·vгр (где vгр – групповая скорость распространения
излучения, для газов vгр ≈ с), получим выражение, подобное (1.32, а):
n
n0
I
1
I0
,
(1.32, б)

42.

n
где I 0 0vгр
n0
I
1
I0
vгр
2 B21 S ( 0 ) 2
,
(1.32, б)
– параметр насыщения для интенсивности
излучения.
Видно, что ρ0 и I0 определяются параметрами квантового перехода и
не зависят от ρ.
Видно также, что величина Δn стремится к нулю (то есть происходит
выравнивание населённостей на уровнях «1» и «2») с ростом как ρ,
так и I.
С учётом (1.31) поглощаемая мощность (1.30,б) будет:
h W n0
P
(1.33)
.
1 2W 2

43.

Рис.1.5. Зависимость
мощности ∆Р,
поглощаемой квантовой
системой, от плотности
энергии падающего
излучения ρ
(интенсивности I,
вероятности поглощения
W)
Графики зависимостей Δn(ρ) и ΔР(ρ)
показаны на рис. 1.5. Проанализируем
предельные случаи. Когда 2Wτ2<<1, что
происходит при малых ρ и I, поглощаемая
мощность ΔР~ρ~I, т.е. зависимости ΔР(ρ) и
ΔР(I) растут линейно. Когда ρ, I велики так,
что 2Wτ2>>1 (в том числе и когда ρ→∞ и
I→∞), получим, что
n0
P( ) h A21 P насыщ ,(1.34)
2
т.е. величина поглощённой мощности
достигает предельной величины ( P насыщ ) и
далее не возрастает.

44. Выводы

Отсюда следует вывод, что ансамбль частиц может поглотить только
такую мощность, которую может излучить за счёт релаксационных
переходов (в данном примере–путём спонтанного излучения с
вероятностью А21).
Таким образом, в двухуровневой системе повышение ρ (и I)
приводит в выравниванию населённостей уровней: n1 и n2 стремятся к
n0/2. При этом для всех возможных значений падающей мощности, в
том числе и бесконечно больших, Δn положительно, откуда следует
важный для практики вывод о том, что в двухуровневой системе с
помощью внешнего излучения невозможно сделать соотношение
населённостей уровней обратным (по отношению к состоянию ТДР).

45. “Форма” и ширина спектральных линий

Понятие оптического спектра. Оптическим спектром называют
совокупность частотных составляющих, на которые может быть
разложено оптическое излучение ансамбля квантовых частиц; т.е.
спектр представляет собой распределение энергии оптического
излучения по длинам волн (частотам). Спектр можно получить с
помощью спектрального прибора как результат обработки
спектрограммы. В зависимости от того, какой тип квантового
перехода связан с исследуемым оптическим излучением квантовой
системы, различают спектры испускания (эмиссионные) и
поглощения (абсорбционные). Оптический спектр отдельных атомов
является линейчатым, т.е. состоящим из отдельных “спектральных
линий”, каждой из которых соответствует дискретное значение длины
волны (частоты). (Принятое в спектроскопической практике понятие
"спектральная линия" обусловлено тем, что монохроматическое
изображение входной щели, формируемое в фокальной плоскости
спектрального прибора, имеет вид линии).

46.

Энергия линии сосредоточена в некотором интервале частот
(говорят, что линия “уширена”). Этот интервал обычно много меньше
абсолютного значения частоты 0, соответствующей максимальному
значению интенсивности излучения линии. Конечная ширина
(«размытость» по энергии) линии, вытекает хотя бы из соотношения
неопределенностей ΔE·τ~ħ, где τ конечно и определяется
релаксационными процессами (происходят без излучения).
Конечность τ и ΔE ведет и к конечной ширине частотной зависимости
вероятности W(ν) перехода. Вид уширения линии играет в квантовой
электронике важную роль. Как будет показано ниже, помимо
релаксационных процессов существуют и другие причины уширения.
Спектр может состоять и из отдельных групп тесно
расположенных спектральных линий, образующих полосы, либо быть
сплошным (непрерывный спектр).

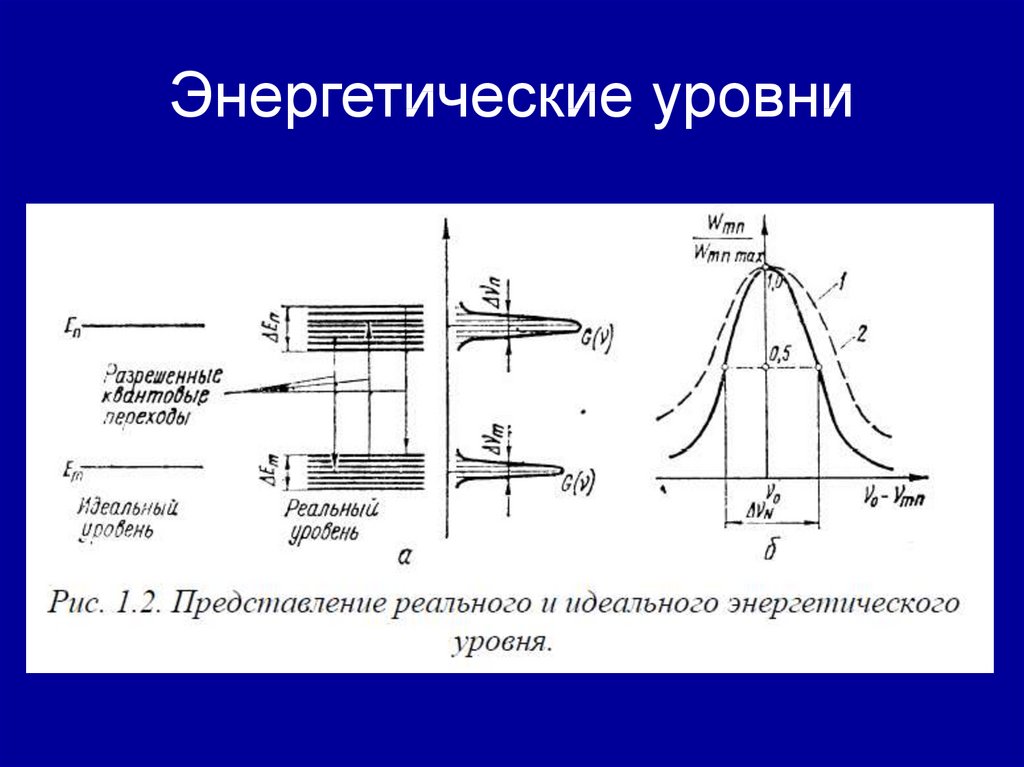
47. Энергетические уровни

48.

Параметры спектральной линии. Под
формой линии понимают частотную
зависимость интенсивности излучения на
данном
квантовом
переходе–I(ν).
Интенсивность излучения I определяется
как поток мощности излучения или как
энергия, проходящая через площадку в 1 см2
в 1 с, и имеет размерность
Рис.
1.2.
Параметры
спектральной линии
[I]=Дж·см–2·с–1=Вт·см–2.
Для типичной спектральной линии, имеющей, как говорят
«колоколообразную» симметричную форму, можно обозначить
следующие ее параметры и характерные точки (рис.1.2):
0–центральная
частота,
соответствующая
максимуму
спектральной интенсивности линии I ( ) : I ( ) o I ( 0 ) I 0 ;
ν' и ν'' – значения частоты, соответствующие половине
интенсивности, т.е. I(ν')=I(ν'')=I(ν0)/2;
=ν''–ν' – ширина линии на уровне I(ν0)/2 (“на полувысоте”),
или коротко: ширина линии.

49.

Введя интегральную интенсивность линии I как: I I ( )d ,
спектральную интенсивность (“форму” линии) I ( ) можно выразить
аналитически двумя способами, через функцию формы линии (или
”форм-фактор”) двух видов: S ( ) и ( ) (Таблица 1.3). Условие
нормировки (1.15) для функции S ( ) может быть получено путём
интегрирования I ( ) , а для функции ( ) – путем вычисления
I ( ) при = 0.

50.

Таблица 1.3. Представление формы спектральной линии
используя “функцию формы”
используя “функцию
линии S ( )
формы” линии ( )
Представление I ( ) I S ( )
(1.14,а) I ( ) I0 ( ) (1.14,б)
I ( )
Условие
нормировки
“функции
формы” линии
Представление
данной
функции через
другую
S ( )d 1
S ( )
( )
( )d
S ( 0 )одн
(1.15,а)
(1.16,а)
( 0 ) 1
( )
S ( )
S ( 0 )
(1.15,б)
(1.16,б)
2
(1.17,а)
одн
(однородное уширение)
Значение
“функции
формы” линии
ln 2
1
S ( 0 )допл
2
(1.17,б)
неодн
допл
при = 0
неодн
(неоднородное уширение)
( 0 ) 1
(1.17,в)

51. Виды уширения спектральных линий

Спектральные линии ансамбля квантовых частиц испытывают
уширение двух видов–однородное и неоднородное.
Однородное
уширение.
При
однородном
уширении
спектральных линий функции формы линии (форм-факторы) для
каждой частицы и всего ансамбля совпадают. Однородное уширение
является следствием релаксационных процессов (см., раздел 1.5) и
бывает естественным, столкновительным, пролётным и др., первые
два типа обычно преобладают, и ширина однородно уширенной
линии одн ест ст .... .
Естественное (или радиационное) уширение
ест , которое
является нижней границей одн , возникает за счёт конечного
времени жизни уровней «1» и «2»: τ1 и τ2. Точное значение ест даёт
квантово-механический подход.

52.

В самом деле, используя соотношение неопределённостей для
обоих уровней:
ΔE1·τ1 ~ ħ
и
ΔE2·τ2 ~ ħ,
можно найти значение ширины уровней ΔE1 и ΔE2, откуда можно
E E2
1
1
получить
.
(1.18)
ест 1
h
2 1 2 2
Столкновительное уширение ст с достаточной точностью
можно
найти,
воспользовавшись
моделью
классического
осциллятора, фаза колебания которого испытывает скачок в момент
столкновения излучающей частицы с другими частицами, со стенкой
кюветы с газом и др., откуда
ст
1
2 ст
,
(1.19)
где τст – интервал времени между двумя последовательными
столкновениями излучающей частицы с другими частицами, со
стенками кюветы и др.

53.

В результате одн будет
одн
j
1
2 j
,
(1.20)
где через τj обозначены 1 , 2 и ст . Важно, что одн не зависит от
частоты перехода ν.
Функции формы линии излучения при однородном уширении
могут быть получены методами электродинамики, и являются
функциями Лоренца:
( одн 2) 2
одн 2
1
.
и ( )одн
S ( )одн
2
2
2
2
( 0 ) одн 2
( 0 ) одн 2
(1.21)
Из (1.21) легко получить значение функции S ( )одн при ν=ν0 (фла (1.17,а) в Таблице 1.3).

54.

При неоднородном уширении форм-факторы каждой частицы и всего
ансамбля различны, а именно, форм-фактор ансамбля является
суперпозицией
форм-факторов
всех
частиц.
Причиной
неоднородного уширения может быть любой процесс, приводящий к
различным условиям возбуждения и (или) излучения различных
частиц или их групп. Примерами неоднородного уширения являются
уширение за счет эффекта Доплера при хаотическом тепловом
движении частиц в газе, а также уширение за счет эффекта Штарка
(расщепление спектральных линий в электрических полях) в
кристаллах.
Специальная теория относительности дает следующее
выражение для сдвига частоты ν, регистрируемой наблюдателем,
если источник, излучающий на частоте ν0, движется относительно
наблюдателя со скоростью u (эффект Доплера):
0 1
2
u
c2
1
u k
,
1
c
где k – единичный вектор, указывающий направление на
наблюдателя, с – скорость света.
(1.22)

55.

Из (1.22) легко получить выражение для ν в нерелятивистском случае
(при малых скоростях, когда u<<c):
0 1
u k
c
(1.23)
Видно, что движение излучающей частицы «к наблюдателю»
приводит к сдвигу частоты излучения в сторону больших ν, а «от
наблюдателя»–меньших ν, причем контур излучения каждой частицы
является лоренцевым с шириной, равной Δνодн (см., рис. 1.3).
Неподвижные (с u=0) или движущиеся с u k =0 ( u k ) частицы,
вносят вклад в суммарный контур ансамбля на центральной частоте
ν0; с u k <0–на частотах ν'<ν0, а с u k >0–на частотах ν''>ν0. Функцию
формы линии S ( )допл
неодн при распределении частиц по скоростям,
описываемым законом Максвелла-Больцмана, можно получить,
исходя из того, что в соответствии с (1.23) вклад в излучение в
частотном интервале ν…ν+dν дают частицы, имеющие скорости в
интервале u…u+du.

56.

Число таких частиц
определяется вероятностью p(u)
в распределении МаксвеллаБольцмана, т.е.
(1.24)
S ( )допл
неодн d p(u) du .
Подставляя в (1.24) p(u),
получим (1.25):
Рис. 1.3. Уширение спектральной
линии за счет эффекта Доплера.
Заштрихованные контура–однородно
уширенные и относящиеся к одной
группе частиц.
a – вклад частиц со скоростью
u·k·cosφ=0, б – вклад частиц со
скоростью u·k·cosφ<0, в – то же при
u·k·cosφ>0.
S ( ) допл
неодн
1
u2
d
exp( 2 )du ,
u0
u0
где u0
2kT
– средняя тепловая
M
скорость частиц.

57.

u k
, найдём связь между du и dν,:
Продифференцировав 0 1
c
c
du d , и подставив её в (1.25), получим гауссовский профиль
0
линии :
S ( ) допл
неодн
допл
где неодн
2
4 ln 2
ln 2
1
допл
неодн
e
( 0 ) 2
допл 2
( неодн
)
,
(1.26)
2 ln 2
2kT
T
– ширина неоднородно
0
7,16 10 7 0
с
M
M
уширенной линии. В последней, “расчётной”, формуле ν0–в Гц, Т – в
К, Μ – масса частицы в а.е.м.
Важно, что в отличие от однородного, при неоднородном
допл
уширении неодн
зависит от центральной частоты перехода ν0.
допл
Значение S ( 0 )допл
неодн 0,9 неодн
(1.17,б): S ( 0 ) допл
неодн 2
1
ln 2
1
допл
неодн
).
приведено в Таблице 1.3 (формула

58.

Сравнение Лоренцевского и Гауссовского контуров (см. рис. 1.4) при
одинаковых интегральной интенсивности и ширине линий показывает,
что лоренцевский контур имеет более пологие «крылья».
Другим типом неоднородного уширения
является уширение за счёт эффекта
Штарка в кристаллах. В кубических кристаллах преобладает механизм однородного уширения линий, а в стёклах – механизм неоднородного уширения. В
примесном кристалле основными приРис. 1.4. Сравнение формчинами неоднородного уширения могут
факторов S(ν) для лоренцевой
быть: при низких температурах – неод(при однородном уширении) и
гауссовой (при неоднородном
нородные внутренние напряжения, обууширении) линий.
словленные низкой симметрией кристалла (чем ближе реальная решетка
кристалла к идеальной кубической, тем
меньше вклад неоднородного уширения в ширину линии);
при высоких температурах – электрон-фононные взаимодействия.

59.

СПАСИБО ЗА ВНИМАНИЕ